归并排序与自然归并排序
归并排序
归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并.
核心步骤讲解
归并排序的核心步骤如下:

可以看出,这算法的核心逻辑就是类似小学语文学文章的一种结构的"总-分-总".
让我们来具体剖析一下,来看看它的思路:
拆分过程:以10 6 7 1这一组为例来看一下拆分过程(核心:使用start, end, mid分别表示开头结尾和中间) :

合并过程:让我么以6,10/1,7这一组为例,来看一下合并过程:最主要的地方就在于传入两组要合并的组,然后创建一个新的数组tmpArr,存放要合并的两个组元素,并将tmpArr中的内容放在源数组中对应位置.

下面是代码:
public class MergeSort {public static void mergeSort(int[] arr) {mergeSortFun(arr, 0, arr.length - 1);}public static void mergeSortFun(int[] arr, int start, int end) {//当start和end重合之后,结束递归if(start >= end) {return;}//找到要切割的位置int mid = (start + end) / 2;//左分支mergeSortFun(arr, start, mid);//右分支mergeSortFun(arr, mid + 1, end);//合并内容merge(arr, start, mid, end);}public static void merge(int[] arr, int left, int mid, int right) {//为了好理解,这里重新用s1,s2,e1,e2表示int s1 = left, e1 = mid, s2 = mid + 1, e2 = right;//定义一个新的数组,用来返回排序好的部分int[] tmpArr = new int[right - left + 1];//用k表示下标(在新创建的数组中的位置)int k = 0;while(s1 <= e1 && s2 <= e2) {if(arr[s1] <= arr[s2]) {tmpArr[k++] = arr[s1++];} else {tmpArr[k++] = arr[s2++];}}//用来存放剩余的部分while(s1 <= e1) {tmpArr[k++] = arr[s1++];}while(s2 <= e2) {tmpArr[k++] = arr[s2++];}//将排序好的数组,放到原来的数组中for(int i = 0; i < tmpArr.length; i++) {arr[i + left] = tmpArr[i];}}public static void main(String[] args) {int[] arr = {10, 6, 7, 1, 3, 9, 4, 2};mergeSort(arr);for(int x : arr) {System.out.print(x + " ");}}
}
归并排序总结
1.归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题.
2.时间复杂度:O(N * logN)
3.空间复杂度:O(N)
4.稳定度:稳定.
海量数据的排序问题
外部排序:排序过程中需要在磁盘等外部存储进行的排序.
eg:内存只有1G,需要排序的数据有100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序.而归并排序是最常用的外部排序.
1.先把文件切分成200份,每个512M
2.分别对512M内容进行排序,因为每个内存都放得下,所以任意排序都可以
3.进行二路归并,同时对200份有序文件进行归并过程,最终结果就有序了.
自然归并排序
自然归并排序是归并排序的一种变体,其主要特点是利用输入数据的初始有序性.自然归并排序的思想是先找到已经有序的子序列,然后合并这些子序列,直至整个数组有序.
核心步骤讲解
1.查找有序子序列:从数组的起始位置开始,找到第一个有序子序列(递增或递减).这可以通过遍历数组来实现.
2.合并有序子序列:将找到的有序子序列进行合并,在合并的过程中,继续查找下一个有序子序列,直到整个数组有序.
3.重复步骤1和2:重复执行步骤1和2,直到整个数组完全有序.
以下是大致过程:

相对于之前的归并排序,这里就不是单纯的向下递归的过程,而是一个寻找子序列的过程,而在归并的过程中,是基本与之前的一致的.所以这里只需要分析一下寻找子序列的过程即可:
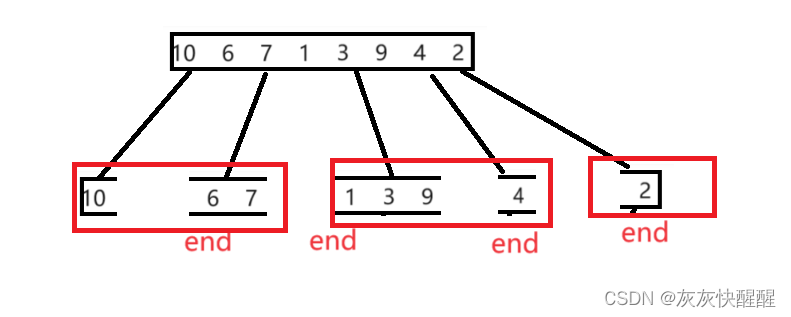
重点:标记的end是上一组的下一个,然后循环时不断标记end,控制为两两一组,进行合并.反复执行上述过程,就可以直接完成.
可能讲的会有点不清楚,请看代码:
import java.util.Arrays;public class NaturalMergeSort {public static void main(String[] args) {int[] array = {10, 6, 7, 1, 3, 9, 4, 2};naturalMergeSort(array);for(int x : array) {System.out.print(x + " ");}}public static void naturalMergeSort(int[] array) {int n = array.length;int[] tempArray = new int[n];int l = -1, m, r;//外部循环,直到不能发现更多的子数组while(l != 0) {l = 0;//内部循环,以寻找并合并有序子数组while (l < n) {m = findNextSortedSubarray(array, l, n, tempArray);//当m 与 n重合时,表明已经找到尾了,退出循环(里和外)if (m == n) {break;}r = findNextSortedSubarray(array, m, n, tempArray);merge(array, l, m, r, tempArray);l = r;}}}//查找下一个有序子数组的方法(返回的是结束位置)private static int findNextSortedSubarray(int[] array, int start, int n, int[] tempArray) {int end = start + 1;while (end < n && array[end - 1] <= array[end]) {end++;}return end;}//二路归并private static void merge(int[] array, int l, int m, int r, int[] tempArray) {int i = l, j = m, k = 0;while (i < m && j < r) {if (array[i] <= array[j]) {tempArray[k++] = array[i++];} else {tempArray[k++] = array[j++];}}while (i < m) {tempArray[k++] = array[i++];}while (j < r) {tempArray[k++] = array[j++];}System.arraycopy(tempArray, 0, array, l, k);}
}
自然归并排序总结
1.这玩意的思路相比于其它排序其实特别恶心,在生产环境中非常不建议使用,你的项目组成员可能会骂街,说你小子装什么逼??(除非是这种情况:就比如你的数据结构老师不知道是为啥心血来潮让你讲这个,整一个反转课堂啥的,那你也没办法~~)
2.时间复杂度:遍历了一次:O(n)
3.空间复杂度:O(n)
相关文章:

归并排序与自然归并排序
归并排序 归并排序(merge - sort)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用.将已有的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序.若将两个有序表合并成一个有序表,成为二路归并. 核心步骤讲解 归并排序的…...

22款奔驰GLS450升级HUD抬头显示 告别低头
随着科技飞速地发展,从汽车领域就可以看出,尤其是汽车的抬头显示器,一经推出就吸引了很多的车主。星骏汇小许Xjh15863 升级HUD抬头显示,HUD与汽车系统进行完整的数据信息连接,整合成大数据,然后将一些重要信…...

关于kotlin的属性委托,报错的,实际原因剖析
报错:Property delegate must have a ‘getValue(SecurityCheckView, KProperty*>)’ method. None of the following functions are suitable 解决方案:就是在根目录的build.gradle中改变 kotlin的插件版本 classpath “org.jetbrains.kotlin:kotli…...
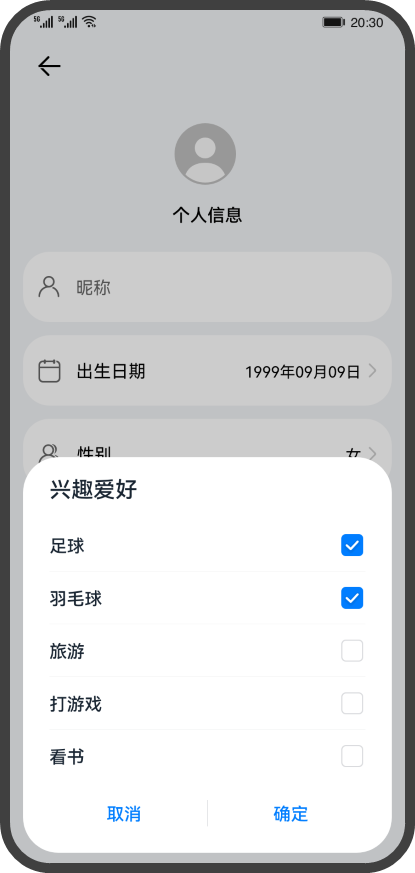
HarmonyOS4.0从零开始的开发教程11给您的应用添加弹窗
HarmonyOS(十)给您的应用添加弹窗 概述 在我们日常使用应用的时候,可能会进行一些敏感的操作,比如删除联系人,这时候我们给应用添加弹窗来提示用户是否需要执行该操作,如下图所示: 弹窗是一种…...

js 同步任务和异步任务
同步任务和异步任务 同步任务 同步任务就是没有被引擎挂起、在主线程上排队执行的任务。只有前一个任务执行完,才会执行下一个任务。同步任务具有堵塞效果。 异步任务 异步任务是被引擎放在一边,不进入主线程进入任务队列的任务。只有引擎认为某个异步任…...
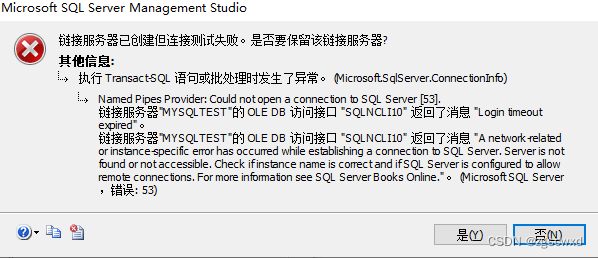
【小白专用】Sql Server 连接Mysql 更新23.12.09
目标 已知mysql连接参数(地址和用户),期望通过Microsoft Sql Server Management Studio (以下简称MSSSMS)连接Mysql,在MSSSMS中直接查询或修改Mysql中的数据。 一般是选最新的版本下载。 选64位还是32位&a…...

DIP——边缘提取与分割
1.使用canny算法进行边缘提取 本实验比较简单,基本思路是对原图像进行一个高斯模糊处理,用于去噪,之后转换为灰度图,直接调用cv库中的canny记性边缘提取。若想直接得到彩色边缘,则通过按位与操作,将原始彩色…...

低代码开发:现实挑战与发展前景
低代码开发是近年来迅速崛起的软件开发方法,让编写应用程序变得更快、更简单。有人说它是美味的膳食,让开发过程高效而满足,但也有人质疑它是垃圾食品,缺乏定制性与深度。 一、什么是低代码 低代码开发是一种基于图形用户界面&…...
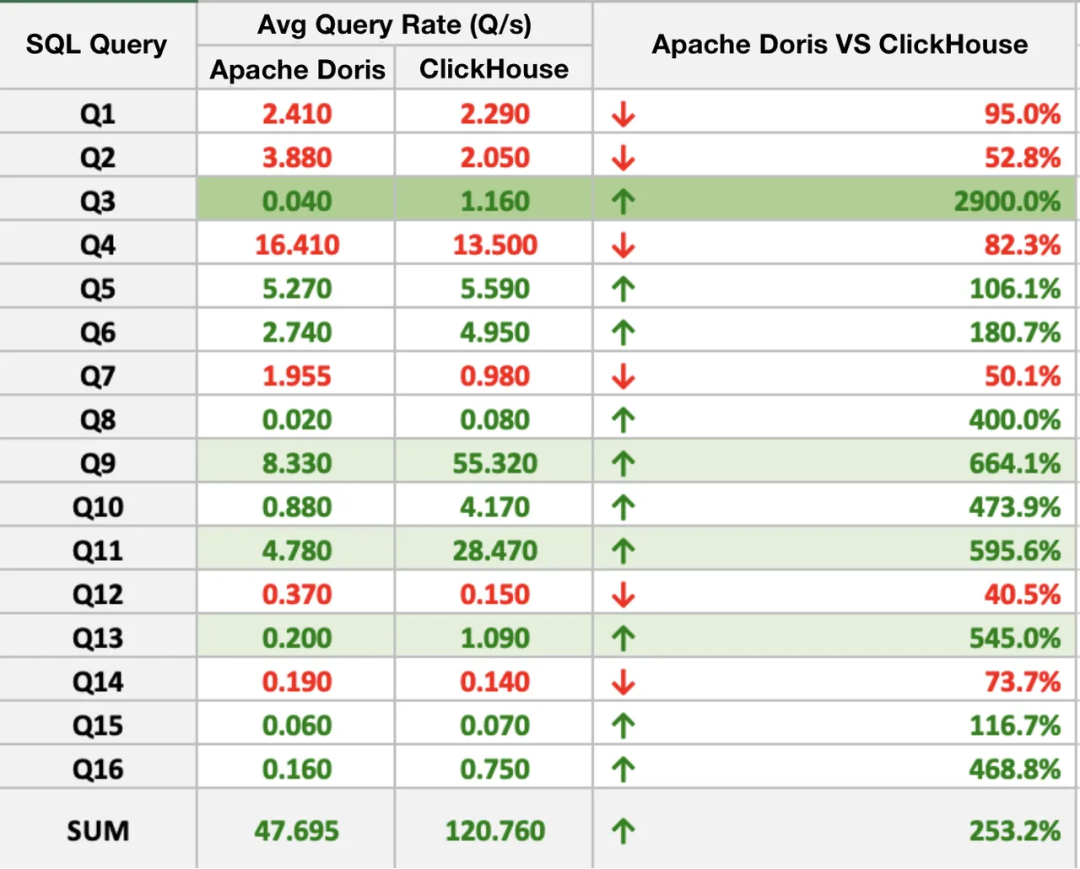
大数据技术7:基于StarRocks统一OALP实时数仓
前言: 大家对StarRocks 的了解可能不及 ClickHouse或者是远不及 ClickHouse 。但是大家可能听说过 Doris ,而 StarRocks 实际上原名叫做 Doris DB ,他相当于是一个加强版的也就是一个 Doris ,也就是说 Doris 所有的功能 StarRocks 都是有的&a…...

C# WPF上位机开发(网络程序界面开发)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 之前我们讨论过,设备之间通讯的方式很多。但是,不知道大家有没有注意,前面谈到的这些通讯方式都需要上位机电脑…...

卡码网语言基础课 | 20. 排队取奶茶
目录 一、 队列的基本认识 二、 队列的操作 2.1 引入头文件 2.2 创建队列 2.3 队列的常见操作 三、 解题 通过本次练习,将会学习到以下C知识点: 队列的基本概念(队头、队尾)和特点(先入先出)入队、出队…...
Angular 进阶之四:SSR 应用场景与局限
应用场景 内容丰富,复杂交互的动态网页,对首屏加载有要求的项目,对 seo 有要求的项目(因为服务端第一次渲染的时候,已经把关键字和标题渲染到响应的 html 中了,爬虫能够抓取到此静态内容,因此更…...
vue2 cron表达式组件
vue2 cron表达式组件 1. 先上图 2. 代码目录 3. 直接上代码 (组件代码太多,直接上压缩包,解压后直接用,压缩包再博客顶部) 4. 使用注:示例代码中使用了element-ui // HomeView.vue<template><…...

git-vscode
git-vscode ctrlshiftp 创建分支 create branch 直接切到新的分支了 切换分支 直接点左下角自己选择 vscode中配置仓库 https://blog.csdn.net/zora_55/article/details/129709251 推送tag tag作用就是在 Git 中,标记存储库历史记录中特定提交的一种方式。t…...
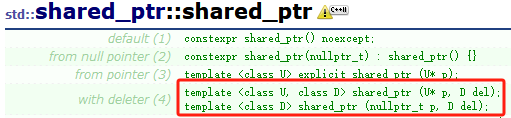
【C++11(三)】智能指针详解--RAII思想循环引用问题
💓博主CSDN主页:杭电码农-NEO💓 ⏩专栏分类:C从入门到精通⏪ 🚚代码仓库:NEO的学习日记🚚 🌹关注我🫵带你学习C 🔝🔝 C11 1. 前言2. 为什么要有智能指针?3. RAII思想…...
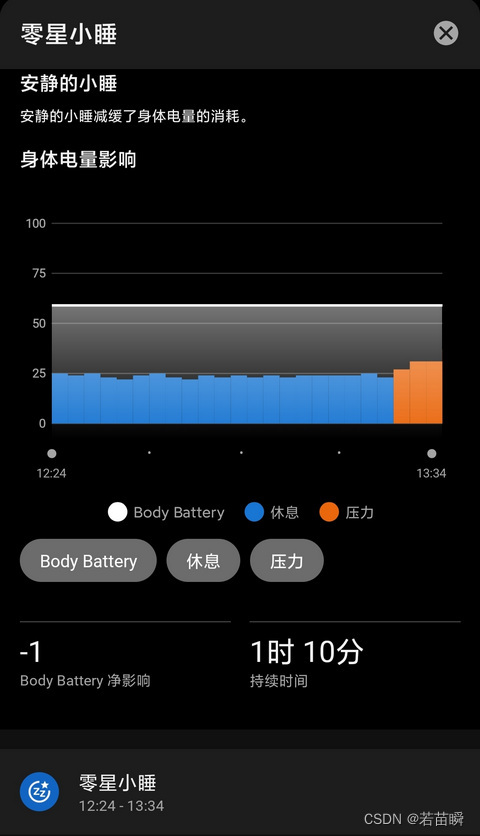
佳明(Garmin) fēnix 7X 增加小睡检测功能
文章目录 (一)零星小睡(二)小睡检测(三)吐槽佳明(3.1)心率检测(3.2)光线感应器(3.3)手表重量(3.4)手表续航 &a…...

二、如何保证架构的质量、架构前期准备、技术填补与崩溃预防、系统重构
1、如何保证架构的质量 -- 稳定性和健壮性 2、正确的选择是良好的开端 -- 架构前期准备 ① 架构师分类:系统架构师、应用架构师、业务架构师 3、技术填补与崩溃预防 4、系统重构...

14、SQL注入——HTTP文件头注入
文章目录 一、HTTP Header概述1.1 HTTP工作原理1.2 HTTP报文类型1.3 较重要的HTTP Header内容 二、HTTP Header注入2.1 HTTP Header注入的前提条件2.2 常见的HTTP Header注入类型 一、HTTP Header概述 1.1 HTTP工作原理 1.2 HTTP报文类型 (1)请求报文 …...
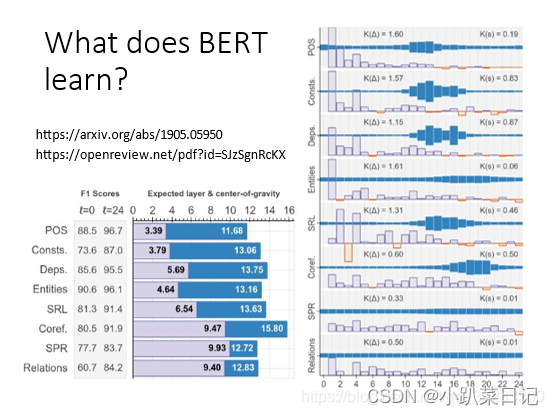
李宏毅bert记录
一、自监督学习(Self-supervised Learning) 在监督学习中,模型的输入为x,若期望输出是y,则在训练的时候需要给模型的期望输出y以判断其误差——有输入和输出标签才能训练监督学习的模型。 自监督学习在没有标注的训练…...

.Net6.0 Microsoft.AspNetCore.Http.Abstractions 2.20 已弃用
您想要升级 Microsoft.AspNetCore.Http.Abstractions 包,您需要注意以下几点: Microsoft.AspNetCore.Http.Abstractions 包在 ASP.NET Core 2.2 版本后已经被标记为过时,因为它已经被包含在 Microsoft.AspNetCore.App 框架引用中12。因此&am…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
