基于python的leetcode算法介绍之递归
文章目录
- 零 算法介绍
- 一 简单示例 辗转相除法
- Leetcode例题与思路
- [509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)
- 解题思路:
- 题解:
- [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)
- 解题思路:
- 题解:
- [面试题 08.06. 汉诺塔问题](https://leetcode.cn/problems/hanota-lcci/)
- 解题思路:
- 题解:
- [94. 二叉树的中序遍历](https://leetcode.cn/problems/binary-tree-inorder-traversal/)
- 解题思路:
- 题解:
- [101. 对称二叉树](https://leetcode.cn/problems/symmetric-tree/)
- 解题思路:
- 题解:
零 算法介绍
递归算法是传统算法中较为简单、基础且实用的一个部分。其核心思想就是通过函数对自身的调用,来实现多层嵌套的过程。而在函数递归的时候,为了保证程序的正常运行,我们需要在程序中设置出口,即需要一个判断条件来终止递归。最简单且常用的递归算法就有通过辗转相除法求两个数的最大公因数问题。
一 简单示例 辗转相除法
辗转相除法,也被称为欧几里得算法,是一种求两个整数的最大公因数(GCD)的经典算法。这个算法基于一个原理:两个整数的最大公因数等于较小数和两数相除余数的最大公因数。
具体步骤如下:
-
将两个数(假设为a和b)中的大数a除以小数b,得到余数r。
-
将b和余数r作为新的两个数,重复步骤1,直到余数为0。
-
余数为0时的除数就是最大公因数。
以下是通过循环求解的思路:
# 被除数 将会等于 除数
# 除数 将会等于 余数
# 考虑能否被递归
# 1. 是否存在相同的算法
# 2. 它的终止条件是否唯一
# 考虑到递归的终止条件
# 递归是从最后一层反向传到第一层
def gcd(a, b): while b != 0: a, b = b, a % b return a print(gcd(48, 18))
# 18
而当我们采用递归的方式实现时:
def gcd(a, b):return gcd(b, a % b) if a % b != 0 else bprint(gcd(48, 18))
# 18
Leetcode例题与思路
接下来,我们列举关于Leetcode的五道例题,并通过递归的方式进行求解:
509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
解题思路:
关于这道题,其实题目中已经给清了思路,我们按照公式整理即可,详情可看题解。
题解:
class Solution:def fib(self, n: int) -> int:return self.fib(n-1) + self.fib(n-2) if n > 1 else n
206. 反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。

解题思路:
这道题的解题思路其实有很多,递归仅是其中一个,由于本章是关于递归算法的介绍,所以不做其他方面的阐述。
那么我们来说一下递归的解法:
首先关于递归算法,我们最需要关注的问题是,它的终止条件是什么? 在这道题里,链表的终止条件似乎是循环到head == None才算结束了。但是问题仅是这样吗?我们需要向下思考一层,那就是当我们在最后一个节点的情况下如何指向上一个节点?在单链表中,显然这是不被允许的!所以,这道题有很关键的一步是,我们判断终止的条件是head.next ≠ None。
当终止条件考虑过后,我们就可以考虑递归的主体了。在主程序中,由于我们的条件保证head.next ≠ None,所以我们可以使得head.next.next = head 这样就可以保证当前节点的下一个节点指向自己。而为了保证我们最后可以拿到逆序后的头节点,我们只需要返回原来链表中的最后一个元素。
题解:
class Solution:def reverseList(self, head: ListNode) -> ListNode:if head is None or head.next is None: # 判断边界并返回逆序后的头节点return headrenode = self.reverseList(head.next)head.next.next = headhead.next = Nonereturn renode
面试题 08.06. 汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
解题思路:
汉诺塔是一道非常经典的递归题目,我也非常喜欢。解这道题最好你玩过汉诺塔,这样你就会有一个基本的逻辑在。不说其他的了,我们来说一下汉诺塔的解题思路:关于这道题,我做一个很形象的比喻:把大象关进冰箱需要几步?只需要三步:打开冰箱门,放进大象,关上冰箱门。忽然这么一说你可能摸不到头脑,但我们可以这么理解:
将汉诺塔从原始柱移到目标柱需要几步?只需要三步:把前N-1层移动到临时柱,把第N层移动到目标柱,把前N-1层在移动到目标柱上。
记住这个逻辑,后面代码中,我将通过raw,temp,aim来替换掉A,B,C。
那这道题目的终止条件是什么呢?
当然是仅剩下一层的时候我该怎么移动了。很简单,从原始柱移动到目标柱就可以了。
那么由于对于N层来说,我们需要把前N-1层移动到临时柱。那么对于前N-1层,那个临时柱就变成了它的目标。提示到这里,聪明的你应该有想法了,那么更精彩的就在代码里了。
题解:
class Solution:def hanota(self, A: List[int], B: List[int], C: List[int]) -> None:n = len(A)raw, temp, aim = A, B, Cself.move(n, raw, temp, aim)def move(self, n, raw, temp, aim):if n == 1:aim.append(raw[-1])raw.pop()return else:self.move(n-1, raw, aim, temp)aim.append(raw[-1]) raw.pop() self.move(n-1,temp, raw, aim)
94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
解题思路:
如果你不知道二叉树的遍历,那么很遗憾,你需要先补习相关知识,之前说的递归的知识其实已经足够了。二叉树和递归其实是相互纠缠的一对儿,所以我们还要讲几到二叉树的题目。
中序遍历:即左子树,根结点,右子树三步走。
而在这道题中,我们先找一下终止条件:即作为树的叶子节点即可返回。
而在程序主体中,我们进需要按照左,中,右的逻辑对列表做拼接即可。
还需要注意一点,就是要小心空树哦。
题解:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:if root == None:return []elif root.left == None and root.right == None:return [root.val]else:my_list = self.inorderTraversal(root.left) if root.left != None else []my_list = my_list + [root.val]my_list = my_list + self.inorderTraversal(root.right) if root.right != None else my_listreturn my_list
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
解题思路:
如何判断一个二叉树是否对称?它仅满足一个条件,即二叉树的左子树和右子树呈现镜像对称。什么意思呢?就是左子树的右节点应该风雨右子树的左节点。
去判断一棵树满足对称二叉树的条件,不如去找他不满足的地方。这是算法那种的一个很重要的思想:判断成功需要挨个证明,但判断失败仅需要一次就行。
那接下来,我们来说一下终止条件:
-
成功:当左右镜像最后都成为None的情况下,就是最终的胜利。
-
迭代:当左右都没到叶子节点的时候,且左右根的值相同。
-
失败:不满足以上条件就是失败。
所以代码很简单可以写成一下形式:
题解:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def isSymmetric(self, root: Optional[TreeNode]) -> bool:def search(left, right):if left == None and right == None:return Trueelif left != None and right != None and left.val == right.val:return search(left.left, right.right) and search(left.right, right.left)else:return Falsereturn search(root.left, root.right) if root != None else True
以上就是关于递归的一些见解,我将不定期的更新该系列,来完善基于python的算法体系。
相关文章:

基于python的leetcode算法介绍之递归
文章目录 零 算法介绍一 简单示例 辗转相除法Leetcode例题与思路[509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)解题思路:题解: [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)解题思路:题解&…...

2023年度佳作:AIGC、AGI、GhatGPT、人工智能大语言模型的崛起与挑战
目录 前言 01 《ChatGPT 驱动软件开发》 内容简介 02 《ChatGPT原理与实战》 内容简介 03 《神经网络与深度学习》 04 《AIGC重塑教育》 内容简介 05 《通用人工智能》 目 录 前言 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一…...
Axure的交互以及情形的介绍
一. 交互 1.1 交互概述 通俗来讲就是,谁用了什么方法做了什么事情,主体"谁"对应的就是axure中的元件,"什么方法"对应的就是交互事件,比如单击事件、双击事件,"什么事情"对应的就是交互…...
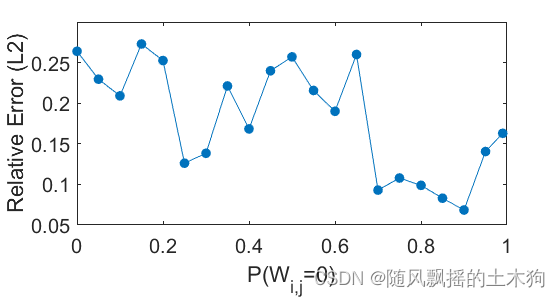
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用 前言 跟往期sobol区别: 1.sobol计算依赖于验证集样本,无需定义变量上下限。 2.SW-ELM自带激活函数,计算具有phi(x)e^x激…...
米游社区表情包整合网站源码
源码介绍 米游社表情包整合网站源码,来自Github大佬的项目,包含米游兔123枚,米游社 玩家12枚,崩坏 星穹铁道112枚,绝区零218枚,NAP32枚,崩坏RPG62枚,崩坏3-1282枚,原神 …...

easyexcel调用公共导出方法导出数据
easyexcel备忘 Slf4j public class ConditionDownloadUtil {//扫描在xboot 包下所有IService 接口的子类, 每次启动服务后, 重新扫描public final static Class[] classesExtendsIService ClassUtil.scanPackageBySuper("cn.exrick.xboot", IService.class).toArra…...
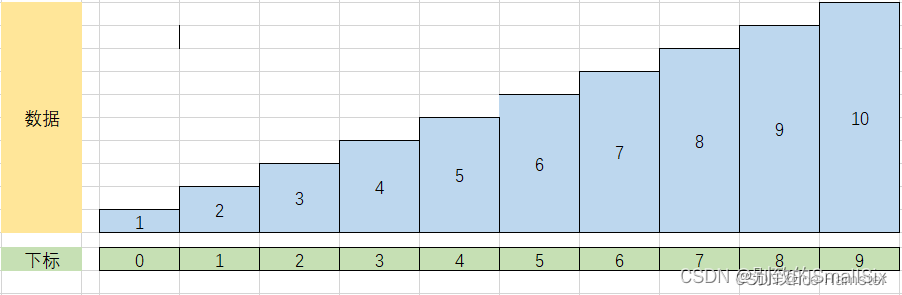
C语言插入排序算法及代码
一、原理 在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 二、代码部分 #include<stdio.h> #include<stdlib.h> int ma…...
2023年中国法拍房用户画像和数据分析
法拍房主要平台 法拍房主要平台有3家,分别是阿里、京东和北交互联平台。目前官方认定纳入网络司法拍卖的平台共有7家,其中阿里资产司法拍卖平台的挂拍量最大。 阿里法拍房 阿里法拍房数据显示2017年,全国法拍房9000套;2018年&a…...

Android 清除临时文件,清空缓存
python 代码: import os import shutil import tracebackdef delete_folder(path):if os.path.exists(path):print(f"删除文件夹: {path}")shutil.rmtree(path)print("删除完成")def delete_file(path):if os.path.exists(path):print(f"删…...
Guava限流神器:RateLimiter使用指南
1. 引言 可能有些小伙伴听到“限流”这个词就觉得头大,感觉像是一个既复杂又枯燥的话题。别急,小黑今天就要用轻松易懂的方式,带咱们一探RateLimiter的究竟。 想象一下,当你去超市排队结账时,如果收银台开得越多&…...

【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序 六大排序之二 插入排序 与 希尔排序1 排序1.1排序的概念 2 插入排序2.1 插入排序原理2.2 排序步骤2.3 代码实现 3 希尔排序3.1 希尔排序原理3.2 排序步骤3.3 代码实现 4 时间复杂度分析 Thanks♪(・ω・)ノ下一篇文章见&am…...

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...
文件操作入门指南
目录 一、为什么使用文件 二、什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 三、文件的打开和关闭 3.1 文件指针 3.2 文件的打开和关闭 四、文件的顺序读写 编辑 🌻深入理解 “流”: 🍂文件的顺序读写函数介绍: …...

Axure之交互与情节与一些实例
目录 一.交互与情节简介 二.ERP登录页到主页的跳转 三.ERP的菜单跳转到各个页面的跳转 四.省市联动 五.手机下拉加载 今天就到这里了,希望帮到你哦!!! 一.交互与情节简介 "交互"通常指的是人与人、人与计算机或物体…...
)
【数据库设计和SQL基础语法】--连接与联接--多表查询与子查询基础(二)
一、子查询基础 1.1 子查询概述 子查询是指在一个查询语句内部嵌套另一个查询语句的过程。子查询可以嵌套在 SELECT、FROM、WHERE 或 HAVING 子句中,用于从数据库中检索数据或执行其他操作。子查询通常返回一个结果集,该结果集可以被包含它的主查询使用…...
Android studio中导入opencv库
具体opencv库的导入流程参考链接:Android Studio开发之路 (五)导入OpenCV以及报错解决 一、出现的错误:NullPointerException: Cannot invoke “java.io.File.toPath()” because “this.mySdkLocation” is null 解决办法&#…...
_基础知识)
Linux(1)_基础知识
第一部分 一、Linux系统概述 创始人:芬兰大学大一的学生写的Linux内核,李纳斯托瓦兹。 Linux时unix的类系统; 特点:多用户 多线程的操作系统; 开源操作系统; 开源项目:操作系统,应用…...

网络相关面试题
简述 TCP 连接的过程(淘系) 参考答案: TCP 协议通过三次握手建立可靠的点对点连接,具体过程是: 首先服务器进入监听状态,然后即可处理连接 第一次握手:建立连接时,客户端发送 syn 包…...

Vue2面试题:说一下对跨域的理解?
http请求分为两大类:普通http请求(如百度请求)和ajax请求(跨域是出现在ajax请求) 同源策略:在浏览器发起ajax请求时,当前的网址和被请求的网址协议、域名、端口号必须完全一致,目的是…...

Axure中如何使用交互样式交互事件交互动作情形
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 目录 一、Axure中交互样式 1、什么是交互样式? 2、交互样式的作用? 3、Axure中如何…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
