【Unity】运行时创建曲线(贝塞尔的运用)
[Unity]运行时创建线(贝塞尔的运用)
1. 实现的目标
在运行状态下创建一条可以使用贝塞尔方法实时编辑的网格曲线。
2. 原理介绍
2.1 曲线的创建
unity建立网格曲线可以参考Unity程序化网格体的实现方法。主要分为顶点,三角面,UV和法线。笔者有类似的文章unity 线绳管道纯代码创建方法_,详细的讲解了网格线的创建方法,这次的不同点在于法线的确立方法上。
2.2贝塞尔曲线点的确立
笔者有文章Unity 贝塞尔曲线的创建_描述了贝塞尔的创建方法。
3. 实现过程
3.1曲线的创建方法
线的组成原理
曲线由横截面圆和中心轴线组成。横截面的法线方向为前后两点向量差,如下图绿色线为中心轴线,A点为横截面所在点,横截面的法线方法为向量 A D ⃗ \vec{AD} AD既向量 C B ⃗ \vec{CB} CB的单位向量;终点和起点的法线方向为自身和前点或者后一点的向量。

代码源码
3.1.1 横截圆的创建
#region 横切圆创建/// <summary>/// 得到管线横切圆/// </summary>/// <param name="Count">段数</param>/// <param name="R">半径</param>/// <returns></returns>Vector3[] CircularSection(int Count, float R){Vector3[] vector3s = new Vector3[Count];float angle = 360 / Count;Vector3 vector3 = new Vector3(R, 0, 0);for (int i = 0; i < Count; i++){//根据角度得到圆的分布点vector3s[i] = vector3.ToAngle(angle * i, Vector3.zero, Vector3.forward);}return vector3s;}#endregion vector3旋转扩展方法
/// <summary>/// 角度旋转/// </summary>/// <param name="vector3"></param>/// <param name="angle">旋转角度</param>/// <param name="center">旋转中心点</param>/// <param name="direction">旋转轴</param>/// <returns></returns>public static Vector3 ToAngle(this Vector3 vector3, float angle, Vector3 center, Vector3 direction){Vector3 pos = center;Quaternion quaternion = Quaternion.AngleAxis(angle, direction);Matrix4x4 matrix = new Matrix4x4();matrix.SetTRS(pos, quaternion, Vector3.one);vector3 = matrix.MultiplyPoint3x4(vector3);return vector3;}
3.1.2 中心线的确立
class LinePoint{Vector3 location;Vector3 direction;public Vector3 Location { get => location; set => location = value; }public Vector3 Direction { get => direction; set => direction = value; }}/// <summary>/// 中心线的确立/// </summary>/// <param name="createPoint">曲线点</param>/// <returns></returns>List<LinePoint> SetLinePoint(Vector3[] createPoint){List<LinePoint> pipePoints = new List<LinePoint>();int length = createPoint.Length;for (int i = 0; i < length; i++){if (i == 0){Vector3 tangent = (createPoint[i + 1] - createPoint[i]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}else if (i == length - 1){Vector3 tangent = (createPoint[i] - createPoint[i - 1]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}else{Vector3 tangent = (createPoint[i+1] - createPoint[i - 1]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}}return pipePoints;}/// <summary>/// 增加中心轴线点/// </summary>/// <param name="location">位置</param>/// <param name="direction">法线</param>void AddPipePoints(Vector3 location, Vector3 direction, ref List<LinePoint> pipePoints){LinePoint pipePoint = new LinePoint();pipePoint.Location = location;pipePoint.Direction = direction;pipePoints.Add(pipePoint);}
3.1.3网格创建
/// <summary>/// 立体网格创建/// </summary>/// <param name="createPoint">创建的点数据</param>/// <param name="circularCount">圆的段数</param>/// <param name="circularR">圆的半径</param>/// <returns></returns>public Mesh CreateLine3D(Vector3[] createPoint, int circularCount, float circularR){//截面圆Vector3[] circul = CircularSection(circularCount, circularR);//中心线List<LinePoint> centreLine = SetLinePoint(createPoint);//网格点数据Vector3[] meshPoint = CreateMeshPoint(centreLine, circul);float uvX = Vector3.Distance(circul[0], circul[1]);//返回网格return CreatMesh(centreLine, meshPoint, circul.Length, uvX);}
/// <summary>/// 创建网格点数据/// </summary>/// <param name="linePoint"></param>/// <param name="circular"></param>/// <returns></returns>Vector3[] CreateMeshPoint(List<LinePoint> linePoint, Vector3[] circular){int length = linePoint.Count;int circularCount = circular.Length;Vector3[] meshPoint = new Vector3[length * circularCount];for (int i = 0; i < length; i++){for (int j = 0; j < circularCount; j++){meshPoint[(i * circularCount) + j] = circular[j].FromToMoveRotation(linePoint[i].Location, linePoint[i].Direction);}}return meshPoint;}/// <summary>/// 网格创建/// </summary>/// <param name="linePoints">线的轴心线组</param>/// <param name="meshPoint">网格点</param>/// <param name="count">段数</param>/// <param name="uvX">uv宽度</param>/// <returns></returns>Mesh CreatMesh(List<LinePoint> linePoints, Vector3[] meshPoint, int count, float uvX){Mesh mesh = new Mesh();mesh.vertices = meshPoint;mesh.triangles = GetTriangles(linePoints.Count, count);mesh.uv = GetUV(linePoints, count, uvX);mesh.RecalculateNormals();mesh.RecalculateBounds();return mesh;}/// <param name="length">线段段数</param>/// <param name="count">横截面段数(也就是圆的段数)</param>/// <returns></returns>int[] GetTriangles(int length, int count){int[] triangles = new int[(count * (length - 1)) * 6];int k = 0;if (count == 1){for (int i = 0; i < length-1; i++){int a = i * 2;triangles[k] = a;triangles[k + 1] = a + 1;triangles[k + 2] = a + 3;triangles[k + 3] = a;triangles[k + 4] = a + 3;triangles[k + 5] = a + 2;k += 6;}}else{for (int i = 0; i < length - 1; i++){for (int j = 0; j < count; j++){if (j == count - 1){// Debug.Log("k=" + k);triangles[k] = (i * count) + j;triangles[k + 1] = (i * count) + 0;triangles[k + 2] = ((i + 1) * count) + 0;triangles[k + 3] = (i * count) + j;triangles[k + 4] = ((i + 1) * count) + 0;triangles[k + 5] = ((i + 1) * count) + j;}else{triangles[k] = (i * count) + j;triangles[k + 1] = (i * count) + j + 1;triangles[k + 2] = ((i + 1) * count) + j + 1;triangles[k + 3] = (i * count) + j;triangles[k + 4] = ((i + 1) * count) + j + 1;triangles[k + 5] = ((i + 1) * count) + j;}k += 6;}}}return triangles;}/// <summary>/// 创建uv/// </summary>/// <param name="linePoints"></param>/// <param name="count"></param>/// <param name="uvX"></param>/// <returns></returns>Vector2[] GetUV(List<LinePoint> linePoints,int count, float uvX){int length = linePoints.Count;if (count == 1) { count = 2; }Vector2[] uvs = new Vector2[(count * length)];float lineDis = 0;int k = 0;for (int i = 0; i < length; i ++){if (i != 0){lineDis += Vector3.Distance(linePoints[i].Location, linePoints[i - 1].Location);}for (int j = 0; j < count; j++){Vector2 vector2;if (j % 2 != 0){vector2 = new Vector2(uvX, lineDis);}else{vector2 = new Vector2(0, lineDis);}uvs[k] = vector2;k += 1;}}return uvs;}
3.2贝塞尔曲线的建立方法
源码
/// <summary>/// 获取绘制点/// </summary>/// <param name="controlPoints"></param>/// <param name="segmentsPerCurve"></param>/// <returns></returns>public List<Vector3> GetDrawingPoints(List<Vector3> controlPoints, int segmentsPerCurve){List<Vector3> points = new List<Vector3>();// 下一段的起始点和上段终点是一个,所以是 i+=3for (int i = 0; i <= controlPoints.Count - 4; i += 3){var p0 = controlPoints[i];var p1 = controlPoints[i + 1];var p2 = controlPoints[i + 2];var p3 = controlPoints[i + 3];float dis = Vector3.Distance(p0, p3);int count = Mathf.CeilToInt(segmentsPerCurve * dis);if (count < segmentsPerCurve){count = segmentsPerCurve;}for (int j = 0; j <= count; j++){var t = j / (float)count;points.Add(CalculateBezierPoint(t, p0, p1, p2, p3));}}return points;}// 三阶公式Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3){Vector3 result;Vector3 p0p1 = (1 - t) * p0 + t * p1;Vector3 p1p2 = (1 - t) * p1 + t * p2;Vector3 p2p3 = (1 - t) * p2 + t * p3;Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;result = (1 - t) * p0p1p2 + t * p1p2p3;return result;}3.3贝塞尔曲线应用
基于上述方法实现了贝塞尔创建,保存,读取,在编辑功能。
案例下载地址
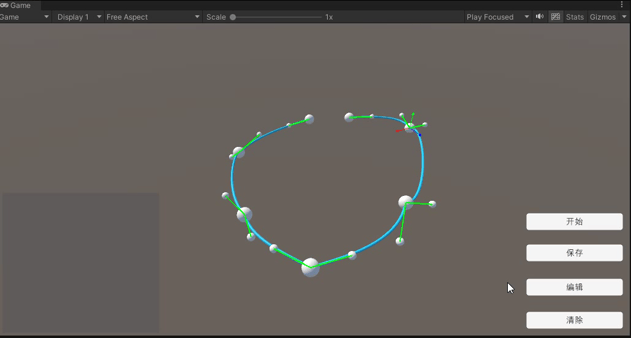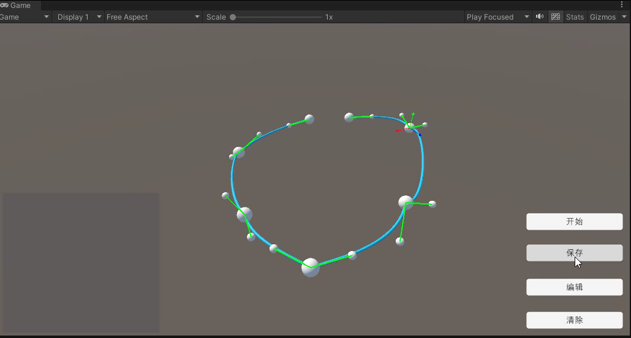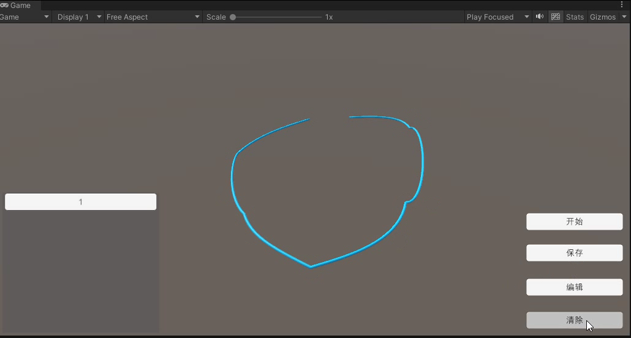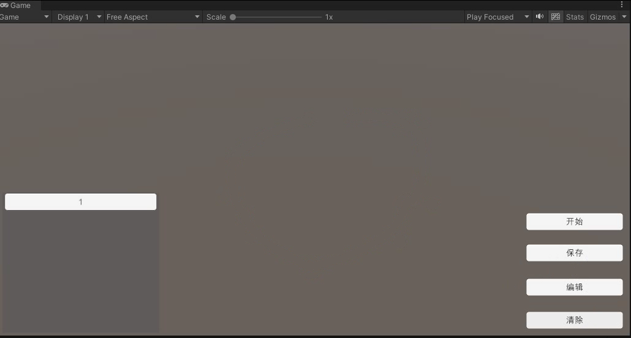
创建曲线

保存曲线
保存方法有两种分别是,长期保存和暂时保存。长期保存是将保存数据写入本地文件,项目重启也可以读取;暂时保存是在项目运行期间保存数据,重启后丢失。demo使用暂时保存的方法
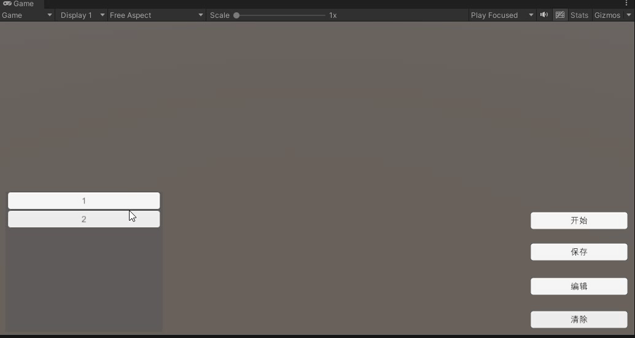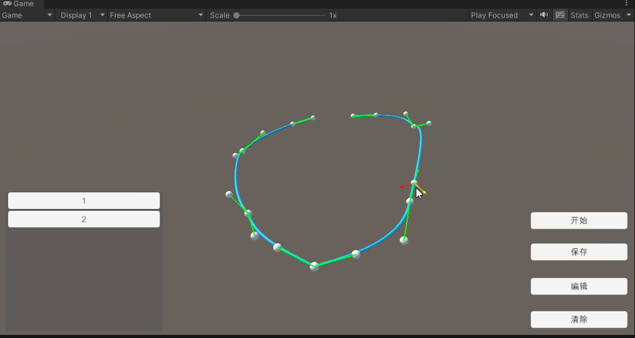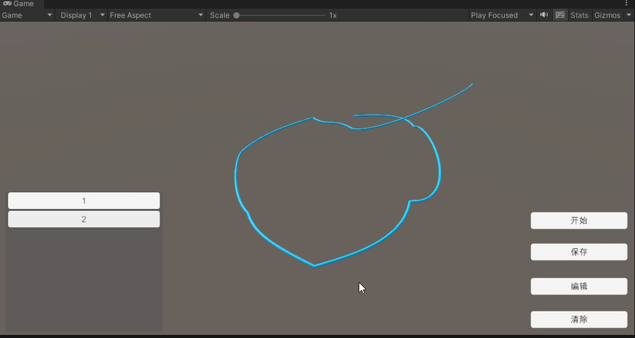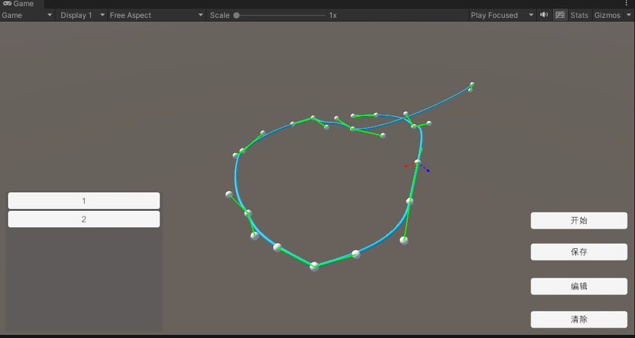
读取再编辑
读取曲线后可以继续编辑当前曲线

曲线浏览
相关文章:

【Unity】运行时创建曲线(贝塞尔的运用)
[Unity]运行时创建线(贝塞尔的运用) 1. 实现的目标 在运行状态下创建一条可以使用贝塞尔方法实时编辑的网格曲线。 2. 原理介绍 2.1 曲线的创建 unity建立网格曲线可以参考Unity程序化网格体的实现方法。主要分为顶点,三角面,…...
基于DSP的IIR数字滤波器(论文+源码)
1.系统设计 在本次基于DSP的IIR数字低通滤波计中,拟以TMS320F28335来作为系统的主控制器,通过ADC0832模数转换芯片来对输入信号进行采集;通过TLC5615来将低通滤波后的信号进行输出;同时结合MATLAB仿真软件,对设计的II…...
Django(一)
1.web框架底层 1.1 网络通信 注意:局域网 个人一般写程序,想要让别人访问:阿里云、腾讯云。 去云平台租服务器(含公网IP)程序放在云服务器 先以局域网为例 我的电脑【服务端】 import socket# 1.监听本机的IP和…...

微信小程序如何利用createIntersectionObserver实现图片懒加载
微信小程序如何利用createIntersectionObserver实现图片懒加载 节点布局相交状态 API 可用于监听两个或多个组件节点在布局位置上的相交状态。这一组API常常可以用于推断某些节点是否可以被用户看见、有多大比例可以被用户看见。 节点布局相交状态 API中有一个 wx.createInter…...
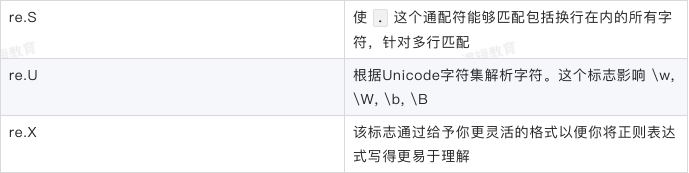
七:爬虫-数据解析之正则表达式
七:正则表达式概述 正则表达式,又称规则表达式,(Regular Expression,在代码中常简写为regex、regexp或RE),是一种文本模式,包括普通字符(例如,a 到 z 之间的字母…...
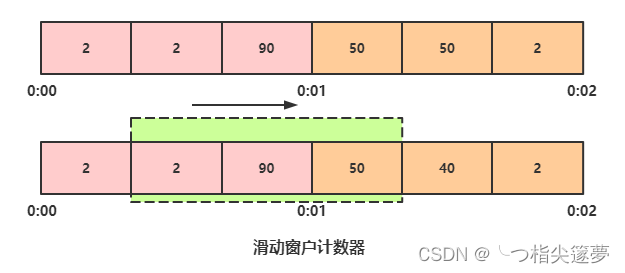
云原生之深入解析亿级流量架构之服务限流思路与方法
一、限流思路 ① 熔断 系统在设计之初就把熔断措施考虑进去,当系统出现问题时,如果短时间内无法修复,系统要自动做出判断,开启熔断开关,拒绝流量访问,避免大流量对后端的过载请求。系统也应该能够动态监测…...

【Python炫酷系列】祝考研的友友们金榜题名吖(完整代码)
文章目录 环境需求完整代码详细分析系列文章环境需求 python3.11.4及以上版本PyCharm Community Edition 2023.2.5pyinstaller6.2.0(可选,这个库用于打包,使程序没有python环境也可以运行,如果想发给好朋友的话需要这个库哦~)【注】 python环境搭建请见:https://want595.…...

KL散度、CrossEntropy详解
文章目录 0. 概述1. 信息量1.1 定义1.2 性质1.3 例子2. 熵 Entropy2.1 定义2.2 公式2.3 例子3. 交叉熵 Cross Entropy3.1 定义3.2 公式3.3 例子4. KL 散度(相对熵)4.1 公式...

【算法】红黑树
一、红黑树介绍 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。 红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来&am…...

2023楚慧杯 WEB方向 部分:(
1、eaaeval 查看源码能看见账号:username169,密码:password196提交这个用户密码可以跳转到页面/dhwiaoubfeuobgeobg.php 通过dirsearch目录爆破可以得到www.zip <?php class Flag{public $a;public $b;public function __construct(){…...

STM32 CAN多节点组网项目实操 挖坑与填坑记录2
系列文章,持续探索CAN多节点通讯, 上一篇文章链接: STM32 CAN多节点组网项目实操 挖坑与填坑记录-CSDN博客文章浏览阅读120次。CAN线性组网项目开发过程中遇到的数据丢包问题,并尝试解决的记录和推测分析。开发了一个多节点线性…...

Flink 数据类型 TypeInformation信息
Flink流应用程序处理的是以数据对象表示的事件流。所以在Flink内部,我么需要能够处理这些对象。它们需要被序列化和反序列化,以便通过网络传送它们;或者从状态后端、检查点和保存点读取它们。为了有效地做到这一点,Flink需要明确知…...

基于python的leetcode算法介绍之递归
文章目录 零 算法介绍一 简单示例 辗转相除法Leetcode例题与思路[509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)解题思路:题解: [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)解题思路:题解&…...

2023年度佳作:AIGC、AGI、GhatGPT、人工智能大语言模型的崛起与挑战
目录 前言 01 《ChatGPT 驱动软件开发》 内容简介 02 《ChatGPT原理与实战》 内容简介 03 《神经网络与深度学习》 04 《AIGC重塑教育》 内容简介 05 《通用人工智能》 目 录 前言 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一…...
Axure的交互以及情形的介绍
一. 交互 1.1 交互概述 通俗来讲就是,谁用了什么方法做了什么事情,主体"谁"对应的就是axure中的元件,"什么方法"对应的就是交互事件,比如单击事件、双击事件,"什么事情"对应的就是交互…...
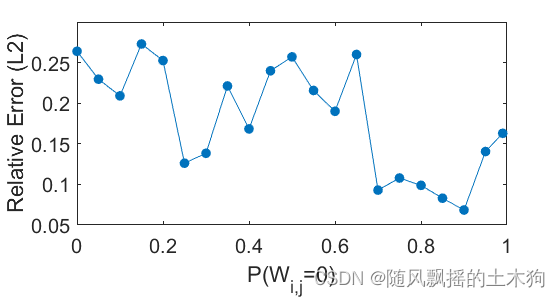
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用 前言 跟往期sobol区别: 1.sobol计算依赖于验证集样本,无需定义变量上下限。 2.SW-ELM自带激活函数,计算具有phi(x)e^x激…...
米游社区表情包整合网站源码
源码介绍 米游社表情包整合网站源码,来自Github大佬的项目,包含米游兔123枚,米游社 玩家12枚,崩坏 星穹铁道112枚,绝区零218枚,NAP32枚,崩坏RPG62枚,崩坏3-1282枚,原神 …...

easyexcel调用公共导出方法导出数据
easyexcel备忘 Slf4j public class ConditionDownloadUtil {//扫描在xboot 包下所有IService 接口的子类, 每次启动服务后, 重新扫描public final static Class[] classesExtendsIService ClassUtil.scanPackageBySuper("cn.exrick.xboot", IService.class).toArra…...
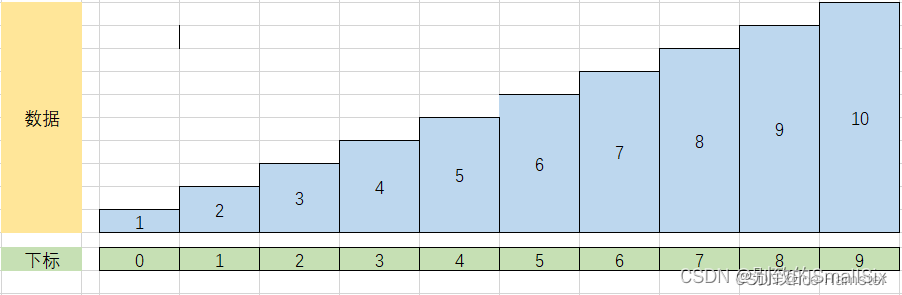
C语言插入排序算法及代码
一、原理 在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 二、代码部分 #include<stdio.h> #include<stdlib.h> int ma…...
2023年中国法拍房用户画像和数据分析
法拍房主要平台 法拍房主要平台有3家,分别是阿里、京东和北交互联平台。目前官方认定纳入网络司法拍卖的平台共有7家,其中阿里资产司法拍卖平台的挂拍量最大。 阿里法拍房 阿里法拍房数据显示2017年,全国法拍房9000套;2018年&a…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
