七:爬虫-数据解析之正则表达式
七:正则表达式概述
正则表达式,又称规则表达式,(Regular Expression,在代码中常简写为regex、regexp或RE),是一种文本模式,包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为"元字符"),是计算机科学的一个概念。正则表达式使用单个字符串来描述、匹配一系列匹配某个语法规则的字符串,通常被用来检索、替换那些符合某个模式(规则)的文本。
- 正则表达式是一个特殊的字符序列,它能帮助你方便的检查一个字符串是否与某种模式匹配。
- 正则表达式使用单个字符串来描述、匹配一系列匹配某个语法规则的字符串。
- 正则表达式是繁琐的,但它是强大的,学会之后的应用会让你除了提高效率外,会给你带来绝对的成就感。
- 许多程序设计语言都支持利用正则表达式进行字符串操作。
正则表达式的应用场景
- 表单验证(例如 : 手机号、邮箱、身份证… )
- 爬虫
正则表达式对Python的支持
普通字符
字母、数字、汉字、下划线、以及没有特殊定义的符号,都是"普通字符"。正则表达式中的普通字符,在匹配的时候,只匹配与自身相同的一个字符。
例如:表达式c,在匹配字符串abcde时,匹配结果是:成功;匹配到的内容是c;匹配到的位置开始于2,结束于3。(注:下标从0开始还是从1开始,因当前编程语言的不同而可能不同)
match()函数
- match(pattern, string, flags=0)
- 第一个参数是正则表达式,如果匹配成功,则返回一个match对象,否则返回一个None
- 第二个参数表示要匹配的字符串
- 第三个参数是标致位用于控制正则表达式的匹配方式 如: 是否区分大小写,多行匹配等等
元字符
正则表达式中使⽤了很多元字符,⽤来表示⼀些特殊的含义或功能
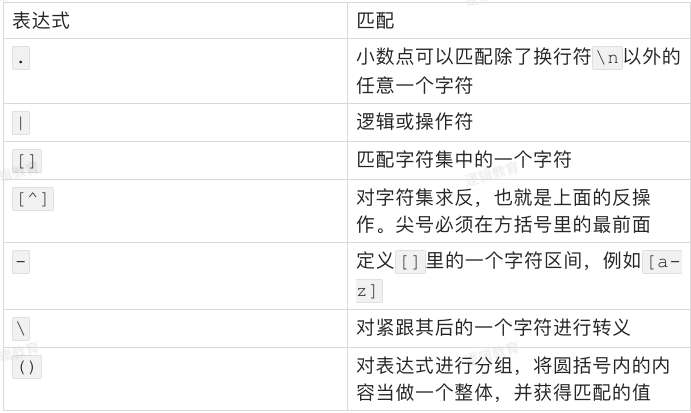
一些无法书写或者具有特殊功能的字符,采用在前面加斜杠""进行转义的方法。
例如下表所示:
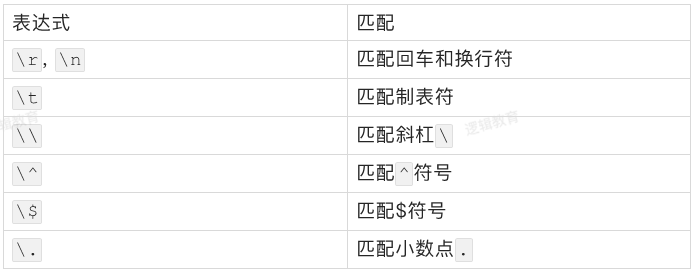
尚未列出的还有问号?、星号*和括号等其他的符号。所有正则表达式中具有特殊含义的字符在匹配自身的时候,都要使用斜杠进行转义。这些转义字符的匹配用法与普通字符类似,也是匹配与之相同的一个字符
预定义匹配字符集
正则表达式中的一些表示方法,可以同时匹配某个预定义字符集中的任意一个字符。比如,表达式\d可以匹配任意一个数字。虽然可以匹配其中任意字符,但是只能是一个,不是多个
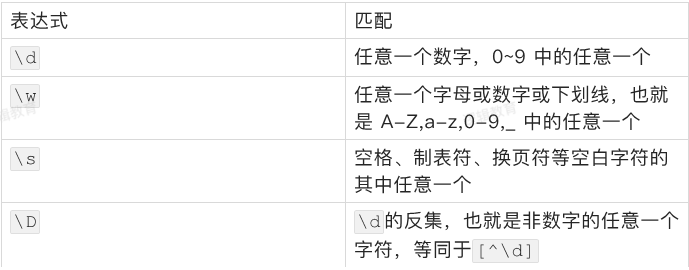

重复匹配
前面的表达式,无论是只能匹配一种字符的表达式,还是可以匹配多种字符其中任意一个的表达式,都只能匹配一次。但是有时候我们需要对某个字段进行重复匹配,例如手机号码13666666666,一般的新手可能会写成\d\d\d\d\d\d\d\d\d\d\d(注意,这不是一个恰当的表达式),不但写着费劲,看着也累,还不⼀定准确恰当。
这种情况可以使用表达式再加上修饰匹配次数的特殊符号{},不但重复书写表达式就可以重复匹配。例如[abcd][abcd]可以写成[abcd]{2}
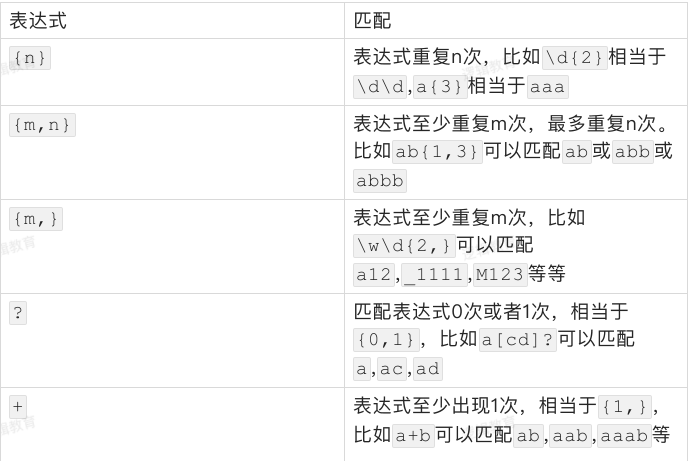

位置匹配和非贪婪匹配
位置匹配
有时候,我们对匹配出现的位置有要求,比如开头、结尾、单词之间等等
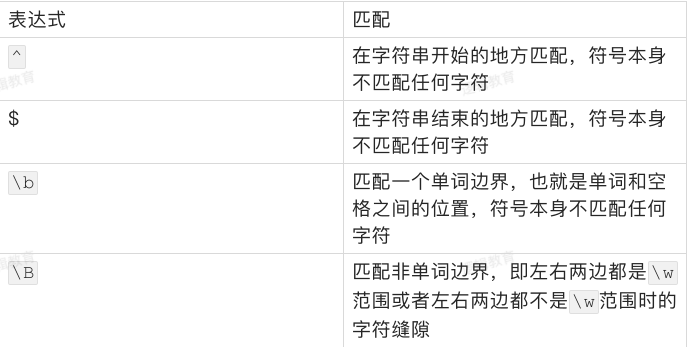
贪婪与非贪婪模式
在重复匹配时,正则表达式默认总是尽可能多的匹配,这被称为贪婪模式。例如,针对文本dxxxdxxxd,表达式(d)(\w+)(d)中的\w+将匹配第一个d和最后一个d之间的所有字符xxxdxxx。可见,\w+在匹配的时候,总是尽可能多的匹配符合它规则的字符。同理,带有?、*和{m,n}的重复匹配表达式都是尽可能地多匹配
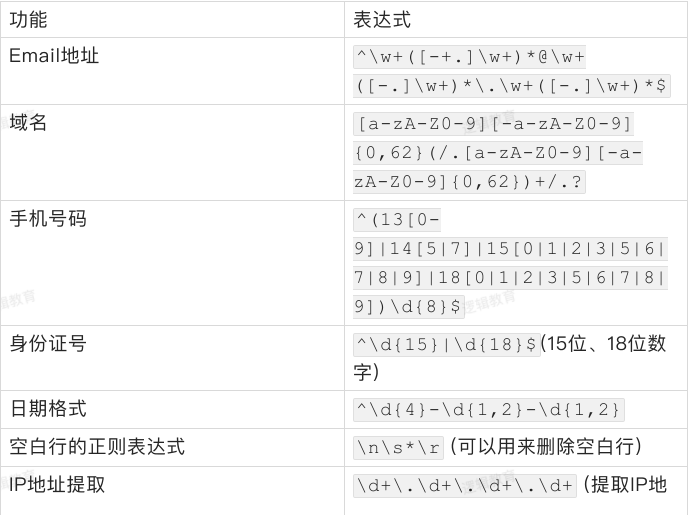
校验数字的相关表达式:

特殊场景的表达式:
re模块常用方法
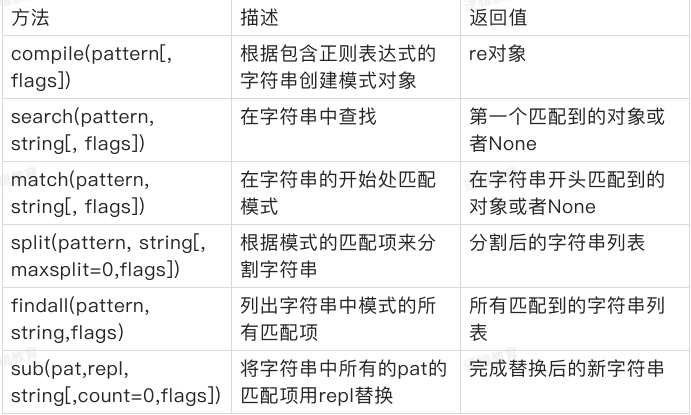
compile(pattern, flags=0)
这个方法是re模块的工厂法,⽤于将字符串形式的正则表达式编译为Pattern模式对象,可以实现更加效率的匹配。第二个参数flag是匹配模式 使用compile()完成一次转换后,再次使用该匹配模式的时候就不能进行转换了。经过compile()转换的正则表达式对象也能使用普通的re方法
flag匹配模式

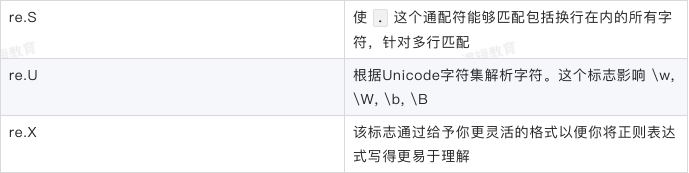
search(pattern, string, flags=0)
在文本内查找,返回第一个匹配到的字符串。它的返回值类型和使用方法与match()是一样的,唯一的区别就是查找的位置不用固定在文本的开头
findall(pattern, string, flags=0)
作为re模块的三大搜索函数之一,findall()和match()、search()的不同之处在于,前两者都是单值匹配,找到一个就忽略后面,直接返回不再查找了。而findall是全文查找,它的返回值是一个匹配到的字符串的列表。这个列表没有group()方法,没有start、end、span,更不是一个匹配对象,仅仅是个列表!如果一项都没有匹配到那么返回一个空列表
split(pattern, string, maxsplit=0, flags=0)
re模块的split()方法和字符串的split()方法很相似,都是利用特定的字符去分割字符串。但是re模块的split()可以使用正则表达式,因此更灵活,更强大
split有个参数maxsplit,用于指定分割的次数
sub(pattern, repl, string, count=0, flags=0)
sub()方法类似字符串的replace()方法,用指定的内容替换匹配到的字符,可以指定替换次数
分组功能
Python的re模块有一个分组功能。所谓的分组就是去已经匹配到的内容再筛选出需要的内容,相当于二次过滤。实现分组靠圆括号(),而获取分组的内容靠的是group()、groups(),其实前面我们已经展示过。re模块里的某个重要方法在分组上,有不同的表现形式,需要区别对待
相关文章:

七:爬虫-数据解析之正则表达式
七:正则表达式概述 正则表达式,又称规则表达式,(Regular Expression,在代码中常简写为regex、regexp或RE),是一种文本模式,包括普通字符(例如,a 到 z 之间的字母…...
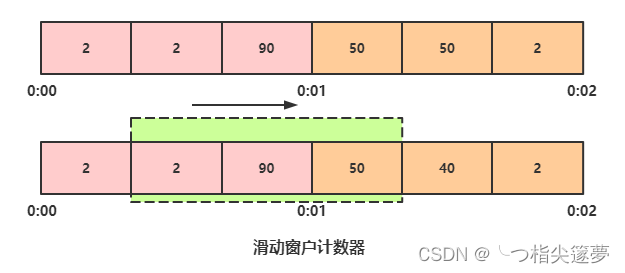
云原生之深入解析亿级流量架构之服务限流思路与方法
一、限流思路 ① 熔断 系统在设计之初就把熔断措施考虑进去,当系统出现问题时,如果短时间内无法修复,系统要自动做出判断,开启熔断开关,拒绝流量访问,避免大流量对后端的过载请求。系统也应该能够动态监测…...

【Python炫酷系列】祝考研的友友们金榜题名吖(完整代码)
文章目录 环境需求完整代码详细分析系列文章环境需求 python3.11.4及以上版本PyCharm Community Edition 2023.2.5pyinstaller6.2.0(可选,这个库用于打包,使程序没有python环境也可以运行,如果想发给好朋友的话需要这个库哦~)【注】 python环境搭建请见:https://want595.…...

KL散度、CrossEntropy详解
文章目录 0. 概述1. 信息量1.1 定义1.2 性质1.3 例子2. 熵 Entropy2.1 定义2.2 公式2.3 例子3. 交叉熵 Cross Entropy3.1 定义3.2 公式3.3 例子4. KL 散度(相对熵)4.1 公式...

【算法】红黑树
一、红黑树介绍 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。 红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来&am…...

2023楚慧杯 WEB方向 部分:(
1、eaaeval 查看源码能看见账号:username169,密码:password196提交这个用户密码可以跳转到页面/dhwiaoubfeuobgeobg.php 通过dirsearch目录爆破可以得到www.zip <?php class Flag{public $a;public $b;public function __construct(){…...

STM32 CAN多节点组网项目实操 挖坑与填坑记录2
系列文章,持续探索CAN多节点通讯, 上一篇文章链接: STM32 CAN多节点组网项目实操 挖坑与填坑记录-CSDN博客文章浏览阅读120次。CAN线性组网项目开发过程中遇到的数据丢包问题,并尝试解决的记录和推测分析。开发了一个多节点线性…...

Flink 数据类型 TypeInformation信息
Flink流应用程序处理的是以数据对象表示的事件流。所以在Flink内部,我么需要能够处理这些对象。它们需要被序列化和反序列化,以便通过网络传送它们;或者从状态后端、检查点和保存点读取它们。为了有效地做到这一点,Flink需要明确知…...

基于python的leetcode算法介绍之递归
文章目录 零 算法介绍一 简单示例 辗转相除法Leetcode例题与思路[509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)解题思路:题解: [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)解题思路:题解&…...

2023年度佳作:AIGC、AGI、GhatGPT、人工智能大语言模型的崛起与挑战
目录 前言 01 《ChatGPT 驱动软件开发》 内容简介 02 《ChatGPT原理与实战》 内容简介 03 《神经网络与深度学习》 04 《AIGC重塑教育》 内容简介 05 《通用人工智能》 目 录 前言 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一…...
Axure的交互以及情形的介绍
一. 交互 1.1 交互概述 通俗来讲就是,谁用了什么方法做了什么事情,主体"谁"对应的就是axure中的元件,"什么方法"对应的就是交互事件,比如单击事件、双击事件,"什么事情"对应的就是交互…...
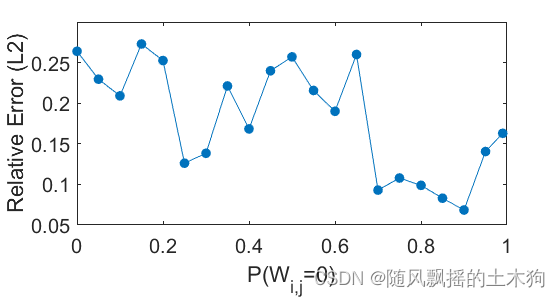
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用 前言 跟往期sobol区别: 1.sobol计算依赖于验证集样本,无需定义变量上下限。 2.SW-ELM自带激活函数,计算具有phi(x)e^x激…...
米游社区表情包整合网站源码
源码介绍 米游社表情包整合网站源码,来自Github大佬的项目,包含米游兔123枚,米游社 玩家12枚,崩坏 星穹铁道112枚,绝区零218枚,NAP32枚,崩坏RPG62枚,崩坏3-1282枚,原神 …...

easyexcel调用公共导出方法导出数据
easyexcel备忘 Slf4j public class ConditionDownloadUtil {//扫描在xboot 包下所有IService 接口的子类, 每次启动服务后, 重新扫描public final static Class[] classesExtendsIService ClassUtil.scanPackageBySuper("cn.exrick.xboot", IService.class).toArra…...
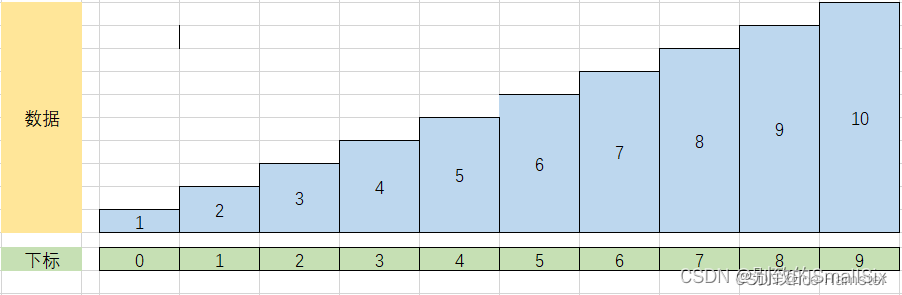
C语言插入排序算法及代码
一、原理 在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 二、代码部分 #include<stdio.h> #include<stdlib.h> int ma…...
2023年中国法拍房用户画像和数据分析
法拍房主要平台 法拍房主要平台有3家,分别是阿里、京东和北交互联平台。目前官方认定纳入网络司法拍卖的平台共有7家,其中阿里资产司法拍卖平台的挂拍量最大。 阿里法拍房 阿里法拍房数据显示2017年,全国法拍房9000套;2018年&a…...

Android 清除临时文件,清空缓存
python 代码: import os import shutil import tracebackdef delete_folder(path):if os.path.exists(path):print(f"删除文件夹: {path}")shutil.rmtree(path)print("删除完成")def delete_file(path):if os.path.exists(path):print(f"删…...
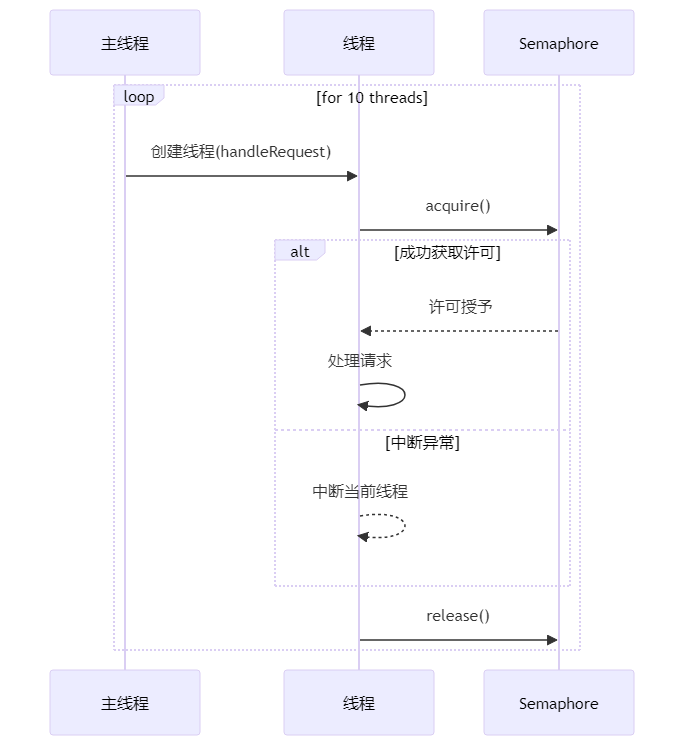
Guava限流神器:RateLimiter使用指南
1. 引言 可能有些小伙伴听到“限流”这个词就觉得头大,感觉像是一个既复杂又枯燥的话题。别急,小黑今天就要用轻松易懂的方式,带咱们一探RateLimiter的究竟。 想象一下,当你去超市排队结账时,如果收银台开得越多&…...

【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序 六大排序之二 插入排序 与 希尔排序1 排序1.1排序的概念 2 插入排序2.1 插入排序原理2.2 排序步骤2.3 代码实现 3 希尔排序3.1 希尔排序原理3.2 排序步骤3.3 代码实现 4 时间复杂度分析 Thanks♪(・ω・)ノ下一篇文章见&am…...

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
