【算法】红黑树
 一、红黑树介绍
一、红黑树介绍
红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。
红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树是一种特化的AVL树(平衡二叉树),都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。
红黑树的每个红色结点的两个子结点都是黑色,从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
以上信息仅供参考,建议查阅专业书籍或者咨询专业人士了解更多信息。
二、红黑树在什么情况下会变得不平衡
红黑树在以下情况下会变得不平衡:
- 插入操作:当插入一个新的节点时,如果插入后的树不再满足红黑树的定义,那么树就会变得不平衡。例如,新插入的节点颜色为红色,而它的父节点颜色也为红色,这就会违反红黑树的定义,导致树变得不平衡。
- 删除操作:当删除一个节点时,如果删除后的树不再满足红黑树的定义,那么树也会变得不平衡。例如,当删除一个红色节点后,其父节点也必须为红色,但如果其父节点也是红色,那么就会违反红黑树的定义,导致树变得不平衡。
为了保持红黑树的平衡性,需要在插入和删除操作时进行一些特定的调整。这些调整包括重新着色节点和重新排列树结构,以确保红黑树的平衡性得到维护。
 三、红黑树的定义是什么
三、红黑树的定义是什么
红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构。它是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。
红黑树满足以下性质:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 每个叶节点(NIL节点,空节点)是黑色。
- 如果一个节点是红色的,则它的两个子节点都是黑色。
- 从任一节点到其每个叶节点的所有路径都包含相同数目的黑色节点。
以上信息仅供参考,建议查阅专业书籍或者咨询专业人士了解更多信息。
四、红黑树和AVL树有哪些区别
红黑树和AVL树的区别主要体现在以下几个方面:
- 平衡的实现机制:红黑树通过颜色和旋转来实现平衡,而AVL树则通过左右子树的高度差来决定旋转。
- 插入效率:红黑树在插入时,由于它只要求部分地达到平衡要求,所以其旋转次数比AVL树要少,因此插入效率更高。
- 统计性能:红黑树能够以O(log2n)的时间复杂度进行搜索、插入、删除操作,而AVL树的性能与其应用场景有关,在查找效率上通常较高。
以上区别仅供参考,建议查阅专业书籍或者咨询专业人士了解更多信息。
 五、红黑树的优缺点
五、红黑树的优缺点
红黑树的优点主要包括:
- 查找、插入和删除操作的平均和最坏情况时间复杂度都是 O(log n),这使得红黑树在大型数据集上的性能非常好。
- 红黑树的平衡性使得它对于一些动态插入、删除元素的应用场景非常适合。
- 红黑树在应用中非常广泛,常被用于各种高性能的数据结构库,例如 STL 中的 set 和 map。
红黑树的缺点主要包括:
- 相比于其他数据结构,红黑树的实现比较复杂,需要维护节点的颜色和平衡。
- 在进行大量插入和删除操作的情况下,可能会造成频繁的树重构,影响性能。
- 红黑树的实现需要额外的空间来存储颜色信息,这意味着相对于其他数据结构,红黑树的空间占用率可能会更高。
总的来说,红黑树是一种高效、自平衡的数据结构,特别适合在需要频繁进行动态插入和删除操作的场景中使用,例如实现高性能的集合和映射。但是在一些空间受限的场景中,可能会有更好的选择。
六、举个例子
以下是一个红黑树的例子:
假设我们有一个红黑树,其中包含了整数1到11,按照从小到大的顺序插入。在插入过程中,我们需要遵守红黑树的定义和性质,通过旋转和重新着色来保持树的平衡。
插入数字1时,因为树为空,所以直接创建一个黑色的根节点1。
接着插入数字2,因为2比1大,所以将2作为1的右子节点,并将其颜色设置为红色。此时树仍然满足红黑树的定义。
然后插入数字3,因为3比2大,所以将3作为2的右子节点,并将其颜色设置为红色。此时,节点2和节点3都是红色,违反了红黑树的定义。为了解决这个问题,我们需要进行旋转和重新着色操作,将节点2变为黑色,节点1变为红色,然后对节点1进行右旋操作。此时树重新恢复平衡。
接下来继续插入数字4到11,每次插入时都根据红黑树的定义进行相应的调整,包括旋转和重新着色操作。最终得到的红黑树就是一个平衡的二叉查找树,其中包含了数字1到11。
这个例子展示了红黑树在插入过程中的自平衡特性,通过旋转和重新着色操作来保持树的平衡性。这种平衡性确保了红黑树在查找、插入和删除操作上的高效性能。
 七、红黑树为什么可以保持平衡
七、红黑树为什么可以保持平衡
红黑树之所以可以保持平衡,是因为它遵守了红黑树的定义和性质。
首先,红黑树是一种平衡的二叉查找树,它的每个节点要么是红色,要么是黑色。在插入和删除操作中,红黑树通过旋转和染色来保持平衡。
其次,红黑树的核心操作是旋转和染色。旋转操作分为左旋和右旋,它们可以帮助恢复树的平衡性。染色操作则是通过改变节点的颜色来保持红黑树的性质。
在插入操作中,如果插入后的树不再满足红黑树的定义,就需要进行旋转和染色操作来恢复平衡。同样地,在删除操作中,如果删除后的树不再满足红黑树的定义,也需要进行旋转和染色操作来恢复平衡。
最后,红黑树的平衡性是通过颜色和旋转来实现的。每个节点都带有颜色属性,并且每个红色节点都必须有两个黑色的子节点(或空子节点)。这种平衡性保证了从根节点到每个叶节点的所有路径都包含相同数目的黑色节点,从而确保了查找、插入和删除操作的效率。
综上所述,红黑树通过遵守红黑树的定义和性质,通过旋转和染色操作来保持平衡,从而实现了高效的查找、插入和删除操作。
八、红黑树的实现原理是什么
红黑树的实现原理是基于二叉查找树,并通过引入额外的颜色和旋转操作来保持树的平衡。
首先,红黑树是一种自平衡的二叉查找树,它满足二叉查找树的性质,即对于树中的每个节点,其左子树中的所有节点的值都小于该节点的值,右子树中的所有节点的值都大于该节点的值。
为了保持平衡,红黑树引入了节点颜色的概念,每个节点都有一个颜色属性,可以是红色或黑色。同时,红黑树还满足以下性质:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(NIL节点,空节点)是黑色。
- 如果一个节点是红色的,则它的两个子节点都是黑色。
- 从任一节点到其每个叶节点的所有路径都包含相同数目的黑色节点。
在插入操作中,当插入一个新的节点时,红黑树会按照二叉查找树的规则进行插入,并将新插入的节点颜色设置为红色。然后,根据红黑树的性质进行调整,包括旋转和重新着色操作,以确保树仍然满足红黑树的定义。
在删除操作中,红黑树会先按照二叉查找树的规则进行删除,然后进行相应的调整来恢复平衡。这可能包括旋转和重新着色操作。
通过遵守这些规则和性质,红黑树能够在插入和删除操作时保持平衡,从而实现高效的查找、插入和删除操作。这种平衡性确保了红黑树在大型数据集上的性能非常好,使其成为许多数据结构库中的首选数据结构之一。
九、一个红黑树C语言用例
#include <stdio.h>
#include <stdlib.h> // 定义红黑树节点结构体
typedef struct node { int data; // 节点存储的数据 int color; // 节点颜色,0表示黑色,1表示红色 struct node *left; // 左子节点 struct node *right; // 右子节点
} Node; // 创建新节点
Node* create_node(int data) { Node *new_node = (Node*)malloc(sizeof(Node)); new_node->data = data; new_node->color = 0; // 初始化为黑色 new_node->left = NULL; new_node->right = NULL; return new_node;
} // 插入新节点
Node* insert(Node *root, int data) { if (root == NULL) { return create_node(data); // 如果树为空,创建新节点作为根节点 } if (data < root->data) { root->left = insert(root->left, data); // 在左子树中插入新节点 } else if (data > root->data) { root->right = insert(root->right, data); // 在右子树中插入新节点 } else { // 如果要插入的数据已经存在,返回NULL return NULL; } // 如果插入后违反了红黑树的性质,需要进行调整 if (is_red(root->right)) { // 如果右子节点是红色,需要进行左旋操作 root = rotate_left(root); } if (is_red(root->left) && !is_red(root->right)) { // 如果左子节点是红色,右子节点是黑色,需要进行右旋操作 root = rotate_right(root); } if (is_red(root->left) && is_red(root->right)) { // 如果左右子节点都是红色,需要进行染色操作 flip_colors(root); } return root; // 返回根节点指针,用于后续操作
} // 判断当前节点是否为红色
int is_red(Node *node) { if (node == NULL) { // 如果节点为空,返回0(黑色) return 0; } else { // 如果节点不为空,判断颜色是否为红色 return node->color == 1; }
} // 进行左旋操作,将当前节点旋转到左边,返回新的根节点指针
Node* rotate_left(Node *z) { Node *y = z->right; // 保存右子节点指针,用于后续操作 z->right = y->left; // 将右子节点的左子节点设为当前节点的右子节点(作为旋转后新的左子节点) y->left = z; // 将当前节点设为旋转后右子节点的左子节点(作为旋转后新的右子节点) z->color = y->color; // 将当前节点的颜色设为旋转后右子节点的颜色(用于后续染色操作) y->color = 1 - z->color; // 将旋转后右子节点的颜色设为当前节点的颜色(用于后续染色操作) return y; // 返回新的根节点指针(旋转后的根节点)
} 十、红黑树的插入操作和删除操作的时间复杂度是多少
十、红黑树的插入操作和删除操作的时间复杂度是多少
插入一个节点的时间复杂度是O(log n),因为红黑树是一种平衡二叉查找树,它可以在O(log n)时间内做查找、插入和删除,这里的n是树中元素的数目。在插入过程中,如果插入的节点不是根节点,那么它会根据红黑树的性质进行旋转和染色操作,以保证树的平衡性。这些操作的时间复杂度都是O(log n)。因此,插入一个节点的时间复杂度也是O(log n)。
十一、红黑树和其他BTS树的区别是什么
红黑树和B树在多个方面存在差异。
- 平衡性:红黑树是一种自平衡二叉查找树,通过旋转和染色操作保持树的平衡性,从而确保高效的查找、插入和删除操作。而B树是一种多路搜索树,它的平衡性没有红黑树严格,但具有更强的鲁棒性。
- 节点颜色:红黑树的节点具有颜色属性,红色和黑色两种。而B树的节点没有颜色属性。
- 查找效率:由于红黑树的平衡性更好,其查找效率通常比B树更高。在红黑树中,查找的时间复杂度为O(log n),而在B树中,查找的时间复杂度为O(log n + k),其中k为关键字数量。
- 应用场景:红黑树常用于实现关联数组、动态集合和查找表等数据结构。而B树则更常用于数据库和文件系统中,因为B树的节点可以包含多个关键字和子节点,能够更有效地利用磁盘等外部存储设备的特性。
综上所述,红黑树和B树在平衡性、节点颜色、查找效率和应用场景等方面存在差异。
 十二、哪种树更适合于数据索引
十二、哪种树更适合于数据索引
红黑树和B树都可以用于数据索引,但它们适用于不同的场景。
红黑树是一种自平衡的二叉查找树,它可以确保查找、插入和删除操作的效率。由于红黑树的平衡性较好,它在处理需要频繁进行查找和更新操作的数据集时表现较好。例如,关联数组、动态集合和查找表等数据结构通常使用红黑树来实现。
B树是一种多路搜索树,它适用于磁盘或其他辅助存储设备上的索引和文件系统。B树的节点可以包含多个关键字和子节点,这使得它更适合于处理大型数据集,特别是在磁盘读写操作方面具有较高的效率。因此,B树在数据库和文件系统中被广泛使用。
总的来说,如果需要频繁进行查找和更新操作,且数据集较小,可以使用红黑树作为索引。如果需要处理大型数据集,特别是在磁盘读写方面具有较高效率的场景下,可以使用B树作为索引。
十三、那在实际应用中,哪一种更适合
在实际应用中,选择红黑树还是B树作为索引取决于具体的应用场景和需求。
如果需要频繁进行查找和更新操作,且数据集较小,红黑树是一种很好的选择。它具有较好的平衡性和查找效率,可以快速定位目标数据,并且适用于需要关联数组、动态集合和查找表等数据结构的情况。
如果需要处理大型数据集,特别是在磁盘读写操作方面具有较高效率的场景下,B树是更好的选择。B树的节点可以包含多个关键字和子节点,使得它更适合于处理大型数据集,并且适用于数据库和文件系统等需要高效磁盘访问的应用。
总之,需要根据具体的应用场景和需求来选择合适的索引结构。在某些情况下,红黑树可能更适合,而在其他情况下,B树可能更为合适。
十四、一个红黑树C语言应用
创建一个红黑树涉及到多个概念和函数实现累积起来比较复杂,至关重要的是实现树节点插入、删除、旋转和重新着色的操作。下面为您简要介绍如何用C语言创建一个基本的红黑树,并展示其中的一些核心功能。此红黑树的实现仅用于学习目的,没有经过充分测试和优化。
下面是一个简单的C语言红黑树实现的框架:
#include <stdio.h>
#include <stdlib.h>typedef enum { RED, BLACK } Color;typedef struct Node {int data;Color color;struct Node *left, *right, *parent;
} Node;typedef struct RBTree {Node *root;
} RBTree;Node* createNode(int data) {Node *newNode = (Node*)malloc(sizeof(Node));newNode->data = data;newNode->color = RED;newNode->left = NULL;newNode->right = NULL;newNode->parent = NULL;return newNode;
}RBTree* createRBTree() {RBTree *tree = (RBTree*)malloc(sizeof(RBTree));tree->root = NULL;return tree;
}// 以下是红黑树操作的伪代码占位
void leftRotate(RBTree *tree, Node *x) {// 执行左旋转操作
}void rightRotate(RBTree *tree, Node *y) {// 执行右旋转操作
}void fixViolation(RBTree *tree, Node *newNode) {// 修复红黑树属性的操作
}void insert(RBTree *tree, int data) {Node *newNode = createNode(data);// 执行常规的BST插入操作// 判断并修复任何可能违反红黑树性质的操作fixViolation(tree, newNode);
}// 主函数,用于测试红黑树
int main() {RBTree* tree = createRBTree();insert(tree, 10);insert(tree, 20);insert(tree, 30);// ...添加更多节点// 执行其他操作,比如删除、查找等// 记得释放红黑树所使用的内存// destroyRBTree(tree);return 0;
}上面的代码展示了一个非常简略的红黑树创建和插入基础的框架。`leftRotate` 和 rightRotate 函数用于调整树结构以维持红黑树特性。`fixViolation` 函数则用于检查并修正可能出现的违反红黑树性质的情况。
要实现一个完整和健壮的红黑树,你需要补完上述示例中缺失的部分,特别是以下几个重要的部分:
1. 实现 leftRotate 和 rightRotate 函数来执行旋转操作。
2. 函数 fixViolation 中实现修复红黑树属性的具体逻辑(处理双红色违规的四种情况:外侧插入、内侧插入、双侧红色和根节点)。
3. 实现搜索、删除节点以及对应的修复函数。
4. 实现内存释放的函数来避免内存泄漏。
注意,这只是一个框架示例代码,真正实现红黑树涉及到许多细节,包括对多种边界条件的处理,以确保树始终维持平衡。因此,如果你需要一个完整的红黑树实现,可以考虑查找完整的图书或者在线资源,或者直接使用现成的库。
 十五、相关链接
十五、相关链接
【数据结构】史上最好理解的红黑树讲解,让你彻底搞懂红黑树-CSDN博客
菜鸟nginx源码剖析数据结构篇(四)红黑树ngx_rbtree_t-CSDN博客
漫画算法:什么是红黑树?(适合初学红黑树小白简单易懂)_红白树 举例-CSDN博客
C语言-B树(B-树)的完整实现_b-树 c 实现-CSDN博客
rbtree 红黑树的 C 语言实现-CSDN博客
相关文章:

【算法】红黑树
一、红黑树介绍 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型的用途是实现关联数组。 红黑树是在1972年由Rudolf Bayer发明的,当时被称为平衡二叉B树(symmetric binary B-trees)。后来&am…...

2023楚慧杯 WEB方向 部分:(
1、eaaeval 查看源码能看见账号:username169,密码:password196提交这个用户密码可以跳转到页面/dhwiaoubfeuobgeobg.php 通过dirsearch目录爆破可以得到www.zip <?php class Flag{public $a;public $b;public function __construct(){…...

STM32 CAN多节点组网项目实操 挖坑与填坑记录2
系列文章,持续探索CAN多节点通讯, 上一篇文章链接: STM32 CAN多节点组网项目实操 挖坑与填坑记录-CSDN博客文章浏览阅读120次。CAN线性组网项目开发过程中遇到的数据丢包问题,并尝试解决的记录和推测分析。开发了一个多节点线性…...

Flink 数据类型 TypeInformation信息
Flink流应用程序处理的是以数据对象表示的事件流。所以在Flink内部,我么需要能够处理这些对象。它们需要被序列化和反序列化,以便通过网络传送它们;或者从状态后端、检查点和保存点读取它们。为了有效地做到这一点,Flink需要明确知…...

基于python的leetcode算法介绍之递归
文章目录 零 算法介绍一 简单示例 辗转相除法Leetcode例题与思路[509. 斐波那契数](https://leetcode.cn/problems/fibonacci-number/)解题思路:题解: [206. 反转链表](https://leetcode.cn/problems/reverse-linked-list/)解题思路:题解&…...

2023年度佳作:AIGC、AGI、GhatGPT、人工智能大语言模型的崛起与挑战
目录 前言 01 《ChatGPT 驱动软件开发》 内容简介 02 《ChatGPT原理与实战》 内容简介 03 《神经网络与深度学习》 04 《AIGC重塑教育》 内容简介 05 《通用人工智能》 目 录 前言 2023年是人工智能大语言模型大爆发的一年,一些概念和英文缩写也在这一…...
Axure的交互以及情形的介绍
一. 交互 1.1 交互概述 通俗来讲就是,谁用了什么方法做了什么事情,主体"谁"对应的就是axure中的元件,"什么方法"对应的就是交互事件,比如单击事件、双击事件,"什么事情"对应的就是交互…...
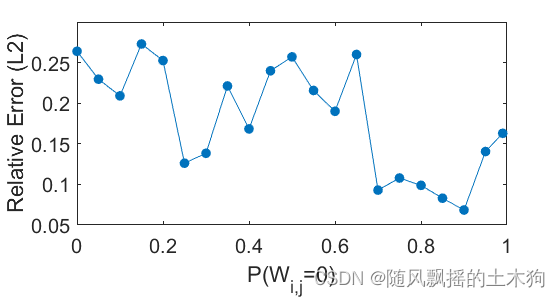
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用
【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用 前言 跟往期sobol区别: 1.sobol计算依赖于验证集样本,无需定义变量上下限。 2.SW-ELM自带激活函数,计算具有phi(x)e^x激…...
米游社区表情包整合网站源码
源码介绍 米游社表情包整合网站源码,来自Github大佬的项目,包含米游兔123枚,米游社 玩家12枚,崩坏 星穹铁道112枚,绝区零218枚,NAP32枚,崩坏RPG62枚,崩坏3-1282枚,原神 …...

easyexcel调用公共导出方法导出数据
easyexcel备忘 Slf4j public class ConditionDownloadUtil {//扫描在xboot 包下所有IService 接口的子类, 每次启动服务后, 重新扫描public final static Class[] classesExtendsIService ClassUtil.scanPackageBySuper("cn.exrick.xboot", IService.class).toArra…...
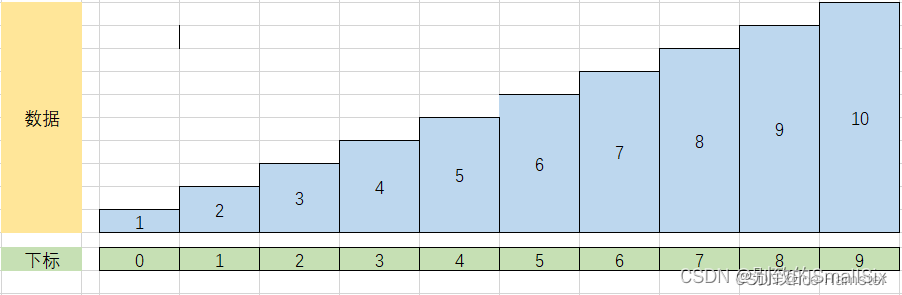
C语言插入排序算法及代码
一、原理 在待排序的数组里,从数组的第二个数字开始,通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。 二、代码部分 #include<stdio.h> #include<stdlib.h> int ma…...
2023年中国法拍房用户画像和数据分析
法拍房主要平台 法拍房主要平台有3家,分别是阿里、京东和北交互联平台。目前官方认定纳入网络司法拍卖的平台共有7家,其中阿里资产司法拍卖平台的挂拍量最大。 阿里法拍房 阿里法拍房数据显示2017年,全国法拍房9000套;2018年&a…...

Android 清除临时文件,清空缓存
python 代码: import os import shutil import tracebackdef delete_folder(path):if os.path.exists(path):print(f"删除文件夹: {path}")shutil.rmtree(path)print("删除完成")def delete_file(path):if os.path.exists(path):print(f"删…...
Guava限流神器:RateLimiter使用指南
1. 引言 可能有些小伙伴听到“限流”这个词就觉得头大,感觉像是一个既复杂又枯燥的话题。别急,小黑今天就要用轻松易懂的方式,带咱们一探RateLimiter的究竟。 想象一下,当你去超市排队结账时,如果收银台开得越多&…...

【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序 六大排序之二 插入排序 与 希尔排序1 排序1.1排序的概念 2 插入排序2.1 插入排序原理2.2 排序步骤2.3 代码实现 3 希尔排序3.1 希尔排序原理3.2 排序步骤3.3 代码实现 4 时间复杂度分析 Thanks♪(・ω・)ノ下一篇文章见&am…...

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...
文件操作入门指南
目录 一、为什么使用文件 二、什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 三、文件的打开和关闭 3.1 文件指针 3.2 文件的打开和关闭 四、文件的顺序读写 编辑 🌻深入理解 “流”: 🍂文件的顺序读写函数介绍: …...

Axure之交互与情节与一些实例
目录 一.交互与情节简介 二.ERP登录页到主页的跳转 三.ERP的菜单跳转到各个页面的跳转 四.省市联动 五.手机下拉加载 今天就到这里了,希望帮到你哦!!! 一.交互与情节简介 "交互"通常指的是人与人、人与计算机或物体…...
)
【数据库设计和SQL基础语法】--连接与联接--多表查询与子查询基础(二)
一、子查询基础 1.1 子查询概述 子查询是指在一个查询语句内部嵌套另一个查询语句的过程。子查询可以嵌套在 SELECT、FROM、WHERE 或 HAVING 子句中,用于从数据库中检索数据或执行其他操作。子查询通常返回一个结果集,该结果集可以被包含它的主查询使用…...
Android studio中导入opencv库
具体opencv库的导入流程参考链接:Android Studio开发之路 (五)导入OpenCV以及报错解决 一、出现的错误:NullPointerException: Cannot invoke “java.io.File.toPath()” because “this.mySdkLocation” is null 解决办法&#…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
