信息论安全与概率论
目录
一. Markov不等式
二. 选择引理
三. Chebyshev不等式
四. Chernov上限
4.1 变量大于
4.2 变量小于
信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。
一. Markov不等式
假定X为非负且为实数的随机变量,令为该变量的数学期望,可得:
理解:代表事件的集合,该定理用来描述概率的上界,且该上界与数学期望相关。
二. 选择引理
令,左边的
代表随机变量,右边
代表该随机变量取值的字母集。假定某函数
,将这些函数集中在一起形成函数集
,另外该函数集内函数的个数
与n无关。给定如下条件:
一定存在该变量中一个具体的数
,满足:
理解:如果经过函数变化后的随机变量的数学期望有上界,那么该函数的某些取值也有上界。
证明:
先做一个简单的改写,令,可以把
看成一个常数,根据联合界定理(union bound),来看一个很有意思的概率:
马上使用刚才谈到的Markov不等式,右边不就是某个变量大于某个数的概率,可得:
条件告诉我们:
直接带入可得:
推导这么久,无非是想说
翻译成人话就是。事件的概率小于1,也就是存在
。接下来就是计算复杂性理论很喜欢用到的一些转化。定理条件说
是有限的,也就是一个常数,并且该常数与n无关,常数在计算复杂性中可以忽略,所以可将
等效为
。
证明完毕。
简化理解:以上推导只是严格按照概率论格式来推导,所以看起来可能有点复杂。让我们来简化下。该定理说明当期望有上限时,至少存在一个变量的值也是这个上限(是不是很简单)。只不是今天的上限满足,(安全领域很喜欢研究渐近性)。
三. Chebyshev不等式
令X为随机变量,可得:
理解:变量的值与期望值不会相差太大,该上限与方差相关。
四. Chernov上限
4.1 变量大于
令X为随机变量,可得:
理解:将s看成一个常数,代表变量大于等于a的概率;
代表对变量操作指数变换
后,求数学期望;该定理反映了变量大于某值时对应的概率有上限,该上限与数学期望有关。与Markov不等式相比,多了一个s,在实际信息论安全推导时,可以设定任何自己想要的参数。
4.2 变量小于
令X为随机变量,可得:
该定理的理解与4.1类似,就不重复描述了。
相关文章:
信息论安全与概率论
目录 一. Markov不等式 二. 选择引理 三. Chebyshev不等式 四. Chernov上限 4.1 变量大于 4.2 变量小于 信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。 一. Markov不等式 假定…...
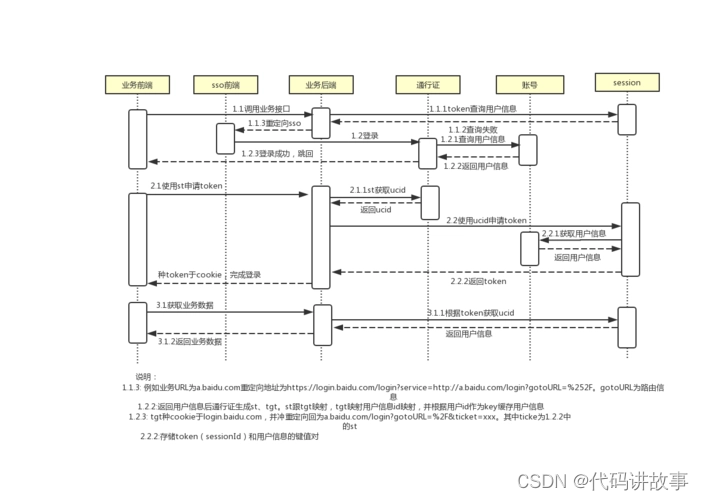
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统。 单点登录(SSO)是一个登录服务层,通过一次登录访问多个应用。使用SSO服务可以提高多系统使用的用户体验和安全性,用户不必记忆多个密…...

Netty Review - 优化Netty通信:如何应对粘包和拆包挑战
文章目录 概述Pre概述场景复现解决办法概览方式一: 特殊分隔符分包 (演示Netty提供的众多方案中的一种)流程分析 方式二: 发送长度(推荐) DelimiterBasedFrameDecoder 源码分析 概述 Pre Netty Review - 借助SimpleTalkRoom初体验…...

vue介绍以及基本指令
目录 一、vue是什么 二、使用vue的准备工作 三、创建vue项目 四、vue插值表达式 五、vue基本指令 六、key的作用 七、v-model 九、指令修饰符 一、vue是什么 Vue是一种用于构建用户界面的JavaScript框架。它可以帮助开发人员构建单页应用程序和复杂的前端应用程序。Vue…...

重塑数字生产力体系,生成式AI将开启云计算未来新十年?
科技云报道原创。 今天我们正身处一个历史的洪流,一个巨变的十字路口。生成式AI让人工智能技术完全破圈,带来了机器学习被大规模采用的历史转折点。 它掀起的新一轮科技革命,远超出我们今天的想象,这意味着一个巨大的历史机遇正…...

JFreeChart 生成图表,并为图表标注特殊点、添加文本标识框
一、项目场景: Java使用JFreeChart库生成图片,主要场景为将具体的数据 可视化 生成曲线图等的图表。 本篇文章主要针对为数据集生成的图表添加特殊点及其标识框。具体包括两种场景:x轴为 时间戳 类型和普通 数值 类型。(y轴都为…...

vue整合axios 未完
一、简介 1、介绍 axios前端异步请求库类似jouery ajax技术,axios用来在前端页面发起一个异步请求,请求之后页面不动,响应回来刷新页面局部;Axios 是一个基于 promise 的 HTTP 库,可以用在浏览器和 node.js 中 2、特…...

java代码编写twitter授权登录
在上一篇内容已经介绍了怎么申请twitter开放的API接口。 下面介绍怎么通过twitter提供的API,进行授权登录功能。 开发者页面设置 首先在开发者页面开启“用户认证设置”,点击edit进行信息编辑。 我的授权登录是个网页,并且只需要进行简单的…...
SK Ecoplant借助亚马逊云科技,海外服务器为环保事业注入新活力
在当今全球面临着资源紧缺和环境挑战的大背景下,数字技术所依赖的海外服务器正成为加速循环经济转型的关键利器。然而,很多企业在整合数字技术到运营中仍然面临着一系列挑战,依然存在低效流程导致的不必要浪费。针对这一问题,SK E…...
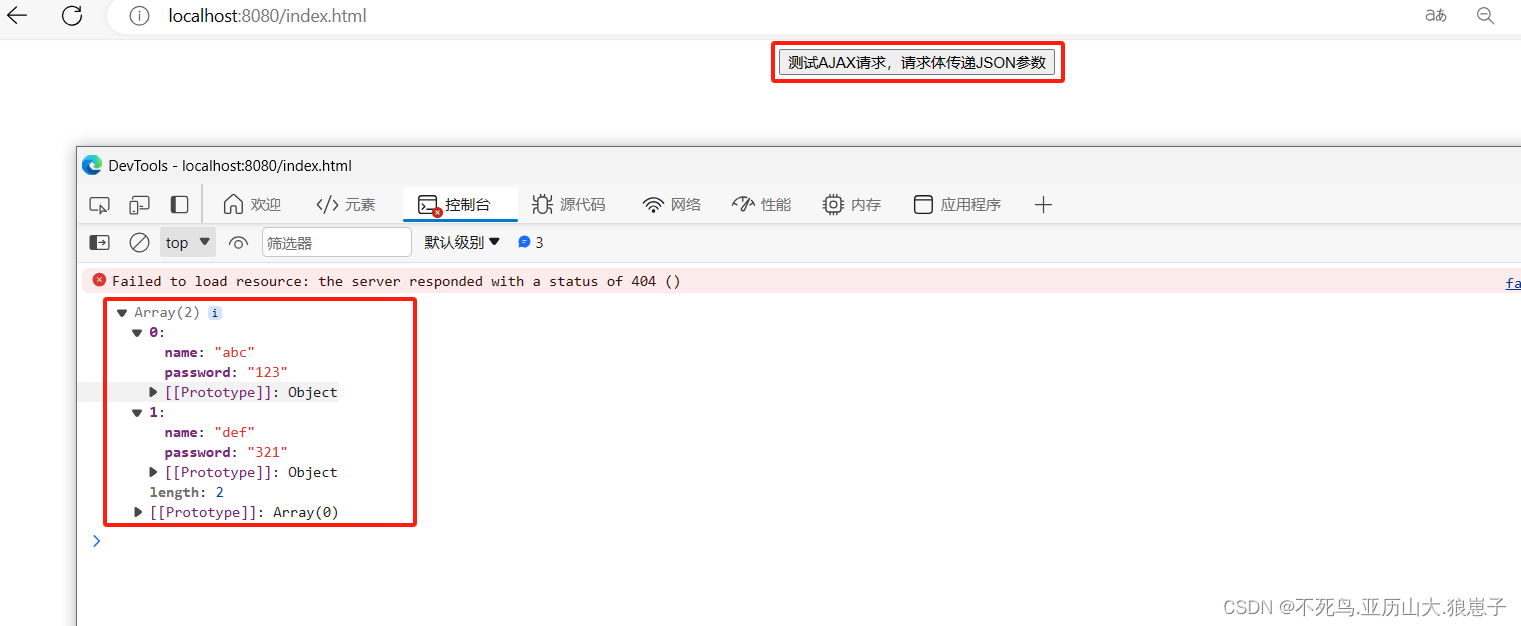
RPC(5):AJAX跨域请求处理
接上一篇RPC(4):HttpClient实现RPC之POST请求进行修改。 1 修改客户端项目 1.1 修改maven文件 修改后配置文件如下: <dependencyManagement><dependencies><dependency><groupId>org.springframework.b…...

用大白话举例子讲明白区块链
什么是区块链?网上这么说: 区块链是一种分布式数据库技术,它以块的形式记录和存储交易数据,并使用密码学算法保证数据的安全性和不可篡改性。每个块都包含了前一个块的哈希值和自身的交易数据,形成了一个不断增长的链条…...

Java URL
URL:统一资源定位符,说白了,就是一个网络 通过URLConnection类可以连接到URL,然后通过URLConnection可以获取读数据的通道。非文本数据用字节流来读取。 读完之后写入本地即可。 public class test {public static void main(S…...
:ETL涉及到的名词解释)
ETL-从1学到100(1/100):ETL涉及到的名词解释
本文章主要介绍ETL和大数据中涉及到名词,同时解释这些名词的含义。由于不是一次性收集这些名词,所以这篇文章将会持续更新,更新日志会存放在本段话下面: 12-19更新:OLTP、OLAP、BI、ETL。 12-20更新:ELT、…...

Jenkins + gitlab 持续集成和持续部署的学习笔记
1. Jenkins 介绍 软件开发生命周期(SLDC, Software Development Life Cycle):它集合了计划、开发、测试、部署的集合。 软件开发瀑布模型 软件的敏捷开发 1.1 持续集成 持续集成 (Continuous integration 简称 CI): 指的是频繁的将代码集成到主干。 持续集成的流…...

R语言【cli】——通过cli_abort用 cli 格式的内容显示错误、警告或信息,内部调用cli_bullets和inline-makeup
cli_abort(message,...,call .envir,.envir parent.frame(),.frame .envir ) 先从那些不需要下大力气理解的参数入手: 参数【.envir】:进行万能表达式编译的环境。 参数【.frame】:抛出上下文。默认用于参数【.trace_bottom】ÿ…...

cka从入门到放弃
无数次想放弃,最后选择了坚持 监控pod日志 监控名为 foobar 的 Pod 的日志,并过滤出具有 unable-access-website 信息的行,然后将 写入到 /opt/KUTR00101/foobar # 解析 监控pod的日志,使用kubectl logs pod-name kubectl logs…...

通过 jekyll 构建 github pages 博客实战笔记
jekyll 搭建教程 jekyll 搭建教程 Gem 安装 Ruby,请访问 下载地址。 Jekyll Jekyll 是一个简单且具备博客特性的静态网站生成器。 Jekyll 中文文档 极客学院中文文档 使用以下命令安装 Jekyll。 $ gem install jekyll在中国可能需要使用代理软件。然后ÿ…...

【AI美图】第09期效果图,AI人工智能汽车+摩托车系列图集
期待中的未来AI汽车 欢迎来到未来的世界,一个充满创新和无限可能的世界,这里有你从未见过的科技奇迹——AI汽车。 想象一下,你站在十字路口,繁忙的交通信号灯在你的视线中闪烁,汽车如潮水般涌来,但是&…...

网线的制作集线器交换机路由器的配置--含思维导图
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 一、网线的制作 1、网线的材料有哪些? 网线 网线是一种用于传输数据信号的电缆,广泛应…...

LLM微调(四)| 微调Llama 2实现Text-to-SQL,并使用LlamaIndex在数据库上进行推理
Llama 2是开源LLM发展的一个巨大里程碑。最大模型及其经过微调的变体位居Hugging Face Open LLM排行榜(https://huggingface.co/spaces/HuggingFaceH4/open_llm_leaderboard)前列。多个基准测试表明,就性能而言,它正在接近GPT-3.5…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
