【数据结构入门精讲 | 第十七篇】一文讲清图及各类图算法
在上一篇中我们进行了的并查集相关练习,在这一篇中我们将学习图的知识点。

目录
- 概念
- 深度优先DFS
- 伪代码
- 广度优先BFS
- 伪代码
- 最短路径算法(Dijkstra)
- 伪代码
- Floyd算法
- 拓扑排序
- 逆拓扑排序
概念
下面介绍几种在对图操作时常用的算法。
深度优先DFS
深度优先搜索(DFS)是一种用于遍历或搜索树、图等数据结构的基本算法。该算法从给定的起点开始,沿着一条路径直到达到最深的节点,然后再回溯到上一个节点,继续探索下一条路径,直到遍历完所有节点或者找到目标节点为止。
具体步骤如下:
-
标记起始节点为已访问。
-
访问当前节点,并获取其所有邻居节点。
-
遍历所有邻居节点,如果该邻居节点未被访问过,则递归地对该邻居节点进行深度优先搜索。
-
重复步骤2和步骤3,直到所有能够到达的节点都被访问过。
DFS算法使用了递归或者栈的机制,在每一轮中尽可能深入地探索,并且只有在到达死胡同(无法继续深入)时才会回溯。DFS并不保证先访问距离起始节点近的节点,而是以深度为导向。
DFS算法可以用于寻找路径、生成拓扑排序、解决回溯问题等,但不保证找到最短路径。其时间复杂度为O(V+E),其中V表示节点数,E表示边数。在树或图的遍历中,DFS通常占用的空间较少,但在最坏情况下可能需要使用大量的栈空间。
简单来说,DFS遵循悬崖勒马回头是岸的原则
拿下图举例:从0一直完左走,走到3,发现没路可走后,回头,继续寻找。
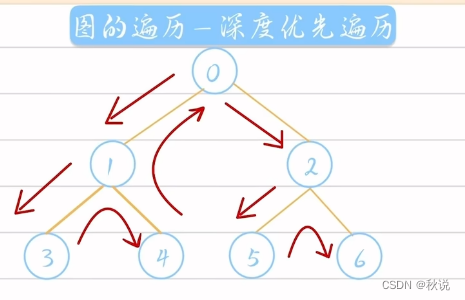
所以:图的深度优先遍历类似于二叉树的先序遍历
伪代码
# 定义图的数据结构
graph = {'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'D': [],'E': ['F'],'F': []
}# 定义访问状态数组
visited = {}# 初始化访问状态
for node in graph:visited[node] = False# 定义DFS函数
def dfs(node):# 标记当前节点为已访问visited[node] = Trueprint(node, end=' ')# 遍历当前节点的邻接节点for neighbor in graph[node]:# 如果邻接节点未被访问,则递归调用DFS函数if not visited[neighbor]:dfs(neighbor)# 从起始节点开始进行DFS
start_node = 'A'
dfs(start_node)广度优先BFS
广度优先搜索(BFS)是一种用于遍历或搜索树、图等数据结构的基本算法。该算法从给定的起点开始,按照距离递增的顺序依次访问其所有邻居节点,并将这些邻居节点加入到一个队列中进行遍历,直到访问到目标节点或者遍历完所有节点。
具体步骤如下:
-
创建一个队列,将起始节点加入队列中并标记为已访问。
-
循环执行以下步骤,直到队列为空:
- 弹出队列头部的节点。
- 访问当前节点,并获取其所有邻居节点。
- 遍历所有邻居节点,如果该邻居节点未被访问过,则将其加入队列尾部,并标记为已访问。
-
循环结束后,所有能够从起始节点到达的节点都已经被访问过了。
BFS算法可以用于寻找最短路径或者解决迷宫等问题,其时间复杂度为O(V+E),其中V表示节点数,E表示边数。相对于深度优先搜索,BFS搜索更具有层次性,能够保证先访问距离起始节点近的节点,因此在寻找最短路径时更为有效。
如何对一个图进行广度优先遍历呢?
方法是:每一层从左到右进行遍历
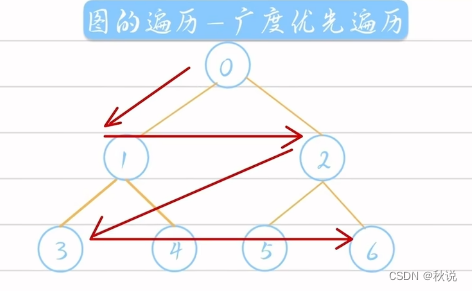
比如下图的结果就是1、2、3、5、6、4、7
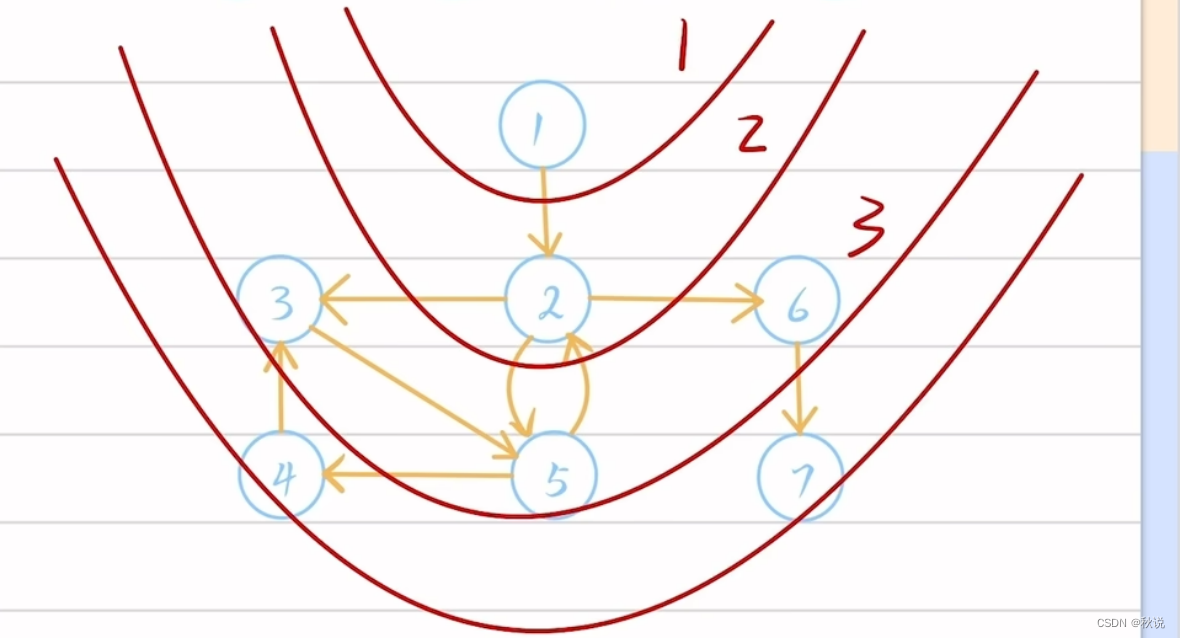
所以图的广度优先遍历类似于树的层次遍历
伪代码
# 定义图的数据结构
graph = {'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'D': [],'E': ['F'],'F': []
}# 定义访问状态数组
visited = {}# 初始化访问状态
for node in graph:visited[node] = False# 定义BFS函数
def bfs(start_node):# 创建队列并将起始节点入队queue = []queue.append(start_node)visited[start_node] = Truewhile queue:# 取出队首节点current_node = queue.pop(0)print(current_node, end=' ')# 遍历当前节点的邻接节点for neighbor in graph[current_node]:# 如果邻接节点未被访问,则将其入队并标记为已访问if not visited[neighbor]:queue.append(neighbor)visited[neighbor] = True# 从起始节点开始进行BFS
start_node = 'A'
bfs(start_node)最短路径算法(Dijkstra)
Dijkstra算法是一种用于解决带权重图中单源最短路径问题的经典算法。它能够找到从起始节点到其他所有节点的最短路径。
该算法的基本思想是通过逐步扩展已知最短路径来逐步确定起始节点到其他节点的最短路径。它维护一个距离字典,记录从起始节点到每个节点的当前最短距离,并使用一个优先队列按照距离的大小进行节点的选择和访问。
具体步骤如下:
-
创建一个距离字典,并将所有节点的距离初始化为无穷大,将起始节点的距离设置为0。
-
将起始节点加入优先队列。
-
循环执行以下步骤,直到优先队列为空:
- 从优先队列中取出距离最小的节点,作为当前节点。
- 遍历当前节点的所有邻居节点:
- 计算从起始节点到当前邻居节点的新距离,即当前节点的距离加上当前节点到邻居节点的边的权重。
- 如果新距离小于邻居节点的当前距离,则更新邻居节点的距离为新距离,并将邻居节点加入优先队列。
-
循环结束后,距离字典中记录了从起始节点到所有其他节点的最短距离。
Dijkstra算法适用于有向图或无向图,但要求图中的边权重必须为非负值。它是一种贪心算法,在每一步都选择当前距离最小的节点进行扩展,直到到达目标节点或遍历完所有节点。该算法的时间复杂度为O((|V|+|E|)log|V|),其中|V|是节点数,|E|是边数。
伪代码
# 定义图的数据结构
graph = {'A': {'B': 5, 'C': 3},'B': {'A': 5, 'C': 1, 'D': 6},'C': {'A': 3, 'B': 1, 'D': 2},'D': {'B': 6, 'C': 2}
}# 定义起始节点和终止节点
start_node = 'A'
end_node = 'D'# 定义距离字典和前驱节点字典
distances = {}
predecessors = {}# 初始化距离字典和前驱节点字典
for node in graph:distances[node] = float('inf') # 将所有节点的距离初始化为无穷大predecessors[node] = None# 设置起始节点的距离为0
distances[start_node] = 0# 定义辅助函数:获取未访问节点中距离最小的节点
def get_min_distance_node(unvisited):min_distance = float('inf')min_node = Nonefor node in unvisited:if distances[node] < min_distance:min_distance = distances[node]min_node = nodereturn min_node# Dijkstra算法主体
unvisited = set(graph.keys())
while unvisited:current_node = get_min_distance_node(unvisited)unvisited.remove(current_node)if current_node == end_node:breakfor neighbor, weight in graph[current_node].items():distance = distances[current_node] + weightif distance < distances[neighbor]:distances[neighbor] = distancepredecessors[neighbor] = current_node# 重构最短路径
path = []
current_node = end_node
while current_node != start_node:path.insert(0, current_node)current_node = predecessors[current_node]
path.insert(0, start_node)# 输出结果
print("最短路径:", path)
print("最短距离:", distances[end_node])
Floyd算法
Floyd算法也称为插点法,是一种用于寻找图中所有节点对之间最短路径的算法,同时也可以用于检测图中是否存在负权回路。
Floyd算法采用动态规划的思想,通过不断更新两个节点之间经过其他节点的最短距离来求解任意两个节点之间的最短路径。具体而言,算法维护一个二维数组 dp,其中 dp[i][j] 表示从节点 i 到节点 j 的最短路径长度。初始化时,若存在一条边从节点 i 到节点 j,则 dp[i][j] 的初值为这条边的边权;否则,dp[i][j] 被赋值为一个足够大的数,表示节点 i 无法到达节点 j。
接下来,我们通过枚举一个中间节点 k,来更新所有节点对之间的最短路径长度。具体而言,如果 dp[i][j] > dp[i][k] + dp[k][j],则说明从节点 i 到节点 j 经过节点 k 的路径比当前的最短路径还要短,此时可以更新 dp[i][j] 的值为 dp[i][k] + dp[k][j]。
重复执行上述步骤,直到枚举完所有的中间节点 k,即可得到任意两个节点之间的最短路径长度。如果在更新过程中发现某些节点之间存在负权回路,则说明无法求解最短路径。
#define INF 99999
#define V 4void floydWarshall(int graph[V][V]) {int dist[V][V], i, j, k;// 初始化最短路径矩阵为图中的边权值for (i = 0; i < V; i++)for (j = 0; j < V; j++)dist[i][j] = graph[i][j];// 动态规划计算最短路径for (k = 0; k < V; k++) {for (i = 0; i < V; i++) {for (j = 0; j < V; j++) {// 如果经过顶点k的路径比直接路径更短,则更新最短路径if (dist[i][k] + dist[k][j] < dist[i][j])dist[i][j] = dist[i][k] + dist[k][j];}}}// 打印最终的最短路径矩阵for (i = 0; i < V; i++) {for (j = 0; j < V; j++) {// 如果路径为无穷大,则打印INF;否则打印最短路径值if (dist[i][j] == INF)printf("%7s", "INF");elseprintf("%7d", dist[i][j]);}printf("\n");}
}拓扑排序
拓扑排序和逆拓扑排序都是用于对有向无环图进行排序的算法。
拓扑排序:对于一个有向无环图,拓扑排序可以得到一组节点的线性序列,使得对于任何一个有向边 (u, v),在序列中节点 u 都排在节点 v 的前面。以下是拓扑排序的伪代码:
# 定义图的数据结构
graph = {'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'D': [],'E': ['F'],'F': []
}# 定义入度字典
in_degree = {}# 初始化入度字典
for node in graph:in_degree[node] = 0for node in graph:for neighbor in graph[node]:in_degree[neighbor] += 1# 定义队列并将入度为0的节点加入队列
queue = []
for node in in_degree:if in_degree[node] == 0:queue.append(node)# 进行拓扑排序
result = []
while queue:current_node = queue.pop(0)result.append(current_node)for neighbor in graph[current_node]:in_degree[neighbor] -= 1if in_degree[neighbor] == 0:queue.append(neighbor)# 输出结果
print(result)
逆拓扑排序
逆拓扑排序:与拓扑排序相反,逆拓扑排序可以得到一组节点的线性序列,使得对于任何一个有向边 (u, v),在序列中节点 v 都排在节点 u 的前面。以下是逆拓扑排序的伪代码:
# 定义图的数据结构
graph = {'A': ['B', 'C'],'B': ['D', 'E'],'C': ['F'],'D': [],'E': ['F'],'F': []
}# 定义出度字典
out_degree = {}# 初始化出度字典
for node in graph:out_degree[node] = len(graph[node])# 定义队列并将出度为0的节点加入队列
queue = []
for node in out_degree:if out_degree[node] == 0:queue.append(node)# 进行逆拓扑排序
result = []
while queue:current_node = queue.pop(0)result.append(current_node)for neighbor in graph[current_node]:out_degree[neighbor] -= 1if out_degree[neighbor] == 0:queue.append(neighbor)# 输出结果
print(result)
至此,图的知识点就介绍完了,在下一篇中我们将进行图的专项练习。
相关文章:

【数据结构入门精讲 | 第十七篇】一文讲清图及各类图算法
在上一篇中我们进行了的并查集相关练习,在这一篇中我们将学习图的知识点。 目录 概念深度优先DFS伪代码 广度优先BFS伪代码 最短路径算法(Dijkstra)伪代码 Floyd算法拓扑排序逆拓扑排序 概念 下面介绍几种在对图操作时常用的算法。 深度优先D…...

Python 直方图的绘制-`hist()`方法(Matplotlib篇-第7讲)
Python 直方图的绘制-hist()方法(Matplotlib篇-第7讲) 🍹博主 侯小啾 感谢您的支持与信赖。☀️ 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹…...

Quartz持久化(springboot整合mybatis版本实现调度任务持久化)--提供源码下载
1、Quartz持久化功能概述 1、实现使用quartz提供的默认11张持久化表存储quartz相关信息。 2、实现定时任务的编辑、启动、关闭、删除。 3、实现自定义持久化表存储quartz定时任务信息。 4、本案例使用springboot整合mybatis框架和MySQL数据库实现持久化 5、提供源码下载 …...

掌握的单词个数 - 华为OD统一考试
OD统一考试 题解: Java / Python / C++ 题目描述 有一个字符串数组 words 和一个字符串 chars。假如可以用 chars 中的字母拼写出 words 中的某个"单词"(字符串),那么我们就认为你掌握了这个单词。 words 的字等仅由 a-z 英文小写宁母组成,例如“abc”。 char…...
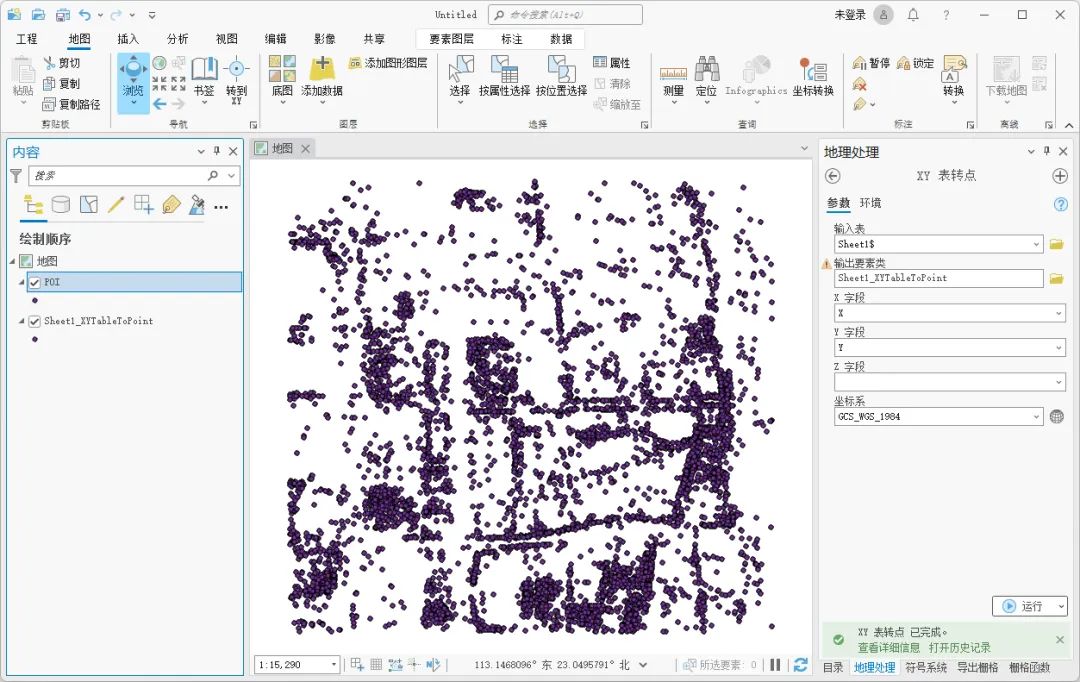
如何使用ArcGIS Pro将Excel表转换为SHP文件
有的时候我们得到的数据是一张张的Excel表格,如果想要在ArcGIS Pro中进行分析或者制图则需要先转换为SHP格式,这里为大家介绍一下转换方法,希望能对你有所帮助。 数据来源 本教程所使用的数据是从水经微图中下载的POI数据,除了P…...
11.1Linux串口应用程序开发
UART简介 UART的全称是Universal Asynchronous Receiver and Transmitter,即异步发送和接收。 串口在嵌入式中用途非常的广泛,主要的用途有: 打印调试信息;外接各种模块:GPS、蓝牙; 串口因为结构简单、稳…...

log4j学习
依赖 <!--log4j依赖--> <dependency><groupId>log4j</groupId><artifactId>log4j</artifactId><version>1.2.17</version> </dependency><!--测试--> <dependency><groupId>org.junit.jupiter</g…...

【Vue2+3入门到实战】(4)Vue基础之指令修饰符 、v-bind对样式增强的操作、v-model应用于其他表单元素 详细示例
目录 一、今日学习目标1.指令补充 二、指令修饰符1.什么是指令修饰符?2.按键修饰符3.v-model修饰符4.事件修饰符 三、v-bind对样式控制的增强-操作class1.语法:2.对象语法3.数组语法4.代码练习 四、京东秒杀-tab栏切换导航高亮1.需求:2.准备代…...
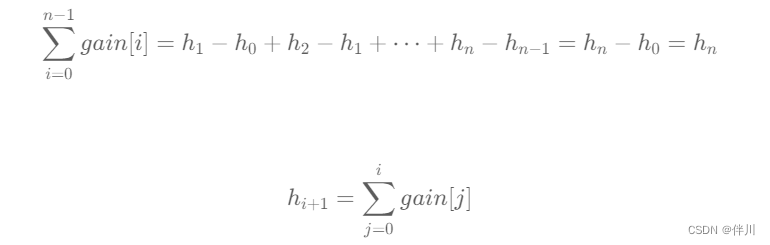
【数据结构和算法】找到最高海拔
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 前缀和的解题模板 2.1.1 最长递增子序列长度 2.1.2 寻找数组中第 k 大的元素 2.1.3 最长公共子序列…...

redis相关问题
1、概述: 1. 非关系型数据库 2. 是分布式缓存数据库 3. 使用 key -value结构存储 2、作用: 用作缓存降低数据库压力,提高性能;可以用作消息队列(削峰、解耦、异步调用) 3、基础语法: 基础命令…...

第41节: Vue3 watch函数
在UniApp中使用Vue3框架时,你可以使用watch函数来观察和响应Vue实例上的数据变化。以下是一个示例,演示了如何在UniApp中使用Vue3框架使用watch函数: <template> <view> <input v-model"message" type"text…...

Centos7:升级gcc、g++到版本5.2.0
背景 Centos7.9版本默认的g版本是4.8.5,在实践golang项目中,用到C14,编译时会报错:gcc: error: unrecognized command line option ‘-stdc14’ 因此,gcc需要升级到更高版本,我这里使用源码编译形式升级到g…...

Pytohn data mode plt
文章目录 文件的读写创建.csv类型的文件,并读取文件创建.xlsx文件 使用Python做图生成数据集切片取值操作修改张量中指定位置的数据 知识点torch.arange(x)torch.tensor(2)Atorch.randn(36).reshape(6,6)shapenumel()reshape(x,y,z)torch.zeros(3,3,4)torch.ones(2,…...

内网离线搭建之----kafka集群
1.系统版本 虚拟机192.168.9.184 虚拟机192.168.9.185 虚拟机192.168.9.186系统 centos7 7.6.1810 2.依赖下载 ps:置顶资源里已经下载好了,直接用!!!!!!!!…...
)
5.1 显示窗口的内容(一)
一,如何显示窗口的内容? 显示器用于在物理硬件(如计算机显示器或触摸屏显示器)上显示窗口的内容。 屏幕API提供的功能允许我们创建同时写入多个窗口和显示的应用程序。屏幕支持多个显示器,但创建和管理使用多个显示器…...
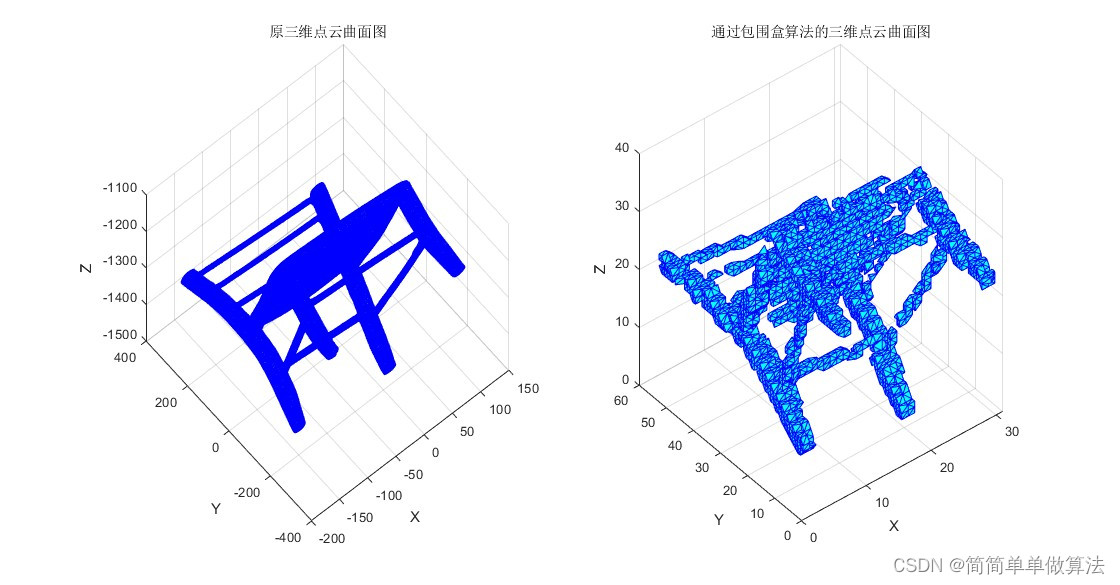
基于包围盒算法的三维点云数据压缩和曲面重建matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1 包围盒构建 4.2 点云压缩 4.3 曲面重建 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ...........................................…...
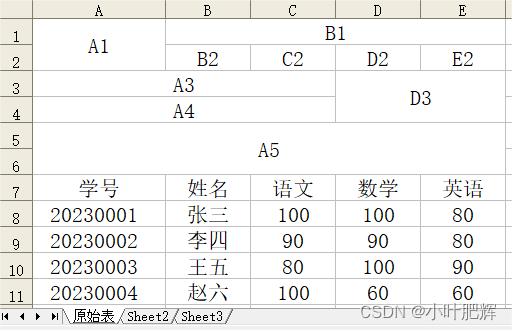
关于Python里xlwings库对Excel表格的操作(十八)
这篇小笔记主要记录如何【设置单元格数据的对齐方式】。前面的小笔记已整理成目录,可点链接去目录寻找所需更方便。 【目录部分内容如下】【点击此处可进入目录】 (1)如何安装导入xlwings库; (2)如何在Wps下…...
VScode远程连接服务器,Pycharm专业版下载及远程连接(深度学习远程篇)
Visual Code、PyCharm专业版,本地和远程交互。 远程连接需要用到SSH协议的技术,常用的代码编辑器vscode 和 pycharm都有此类功能。社区版的pycharm是免费的,但是社区版不支持ssh连接服务器,只有专业版才可以,需要破解…...
------$bus)
Vue2和Vue3组件间通信方式汇总(3)------$bus
组件间通信方式是前端必不可少的知识点,前端开发经常会遇到组件间通信的情况,而且也是前端开发面试常问的知识点之一。接下来开始组件间通信方式第三弹------$bus,并讲讲分别在Vue2、Vue3中的表现。 Vue2Vue3组件间通信方式汇总(1)…...
PyTorch加载数据以及Tensorboard的使用
一、PyTorch加载数据初认识 Dataset:提供一种方式去获取数据及其label 如何获取每一个数据及其label 总共有多少的数据 Dataloader:为后面的网络提供不同的数据形式 数据集 在编译器中导入Dataset from torch.utils.data import Dataset 可以在jupyter中查看Dataset官方文档&…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
