【数据结构和算法】---二叉树(2)--堆的实现和应用
目录
- 一、堆的概念及结构
- 二、堆结构的实现
- 2.1堆向下调整算法
- 2.2堆向上调整算法
- 2.3删除堆顶元素
- 2.4插入元素
- 2.5其他函数接口
- 三、堆结构的应用
- 3.1堆排序
- 3.2Top-k问题
- 四、堆概念及结构相关题目
一、堆的概念及结构
如果有一个数字集合,并把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,且在逻辑结构(即二叉树)中,如果每个父亲节点都大于它的孩子节点那么此堆可以称为大堆;那么如果每个父亲节点都小于它的孩子节点那么此堆可以称为小堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
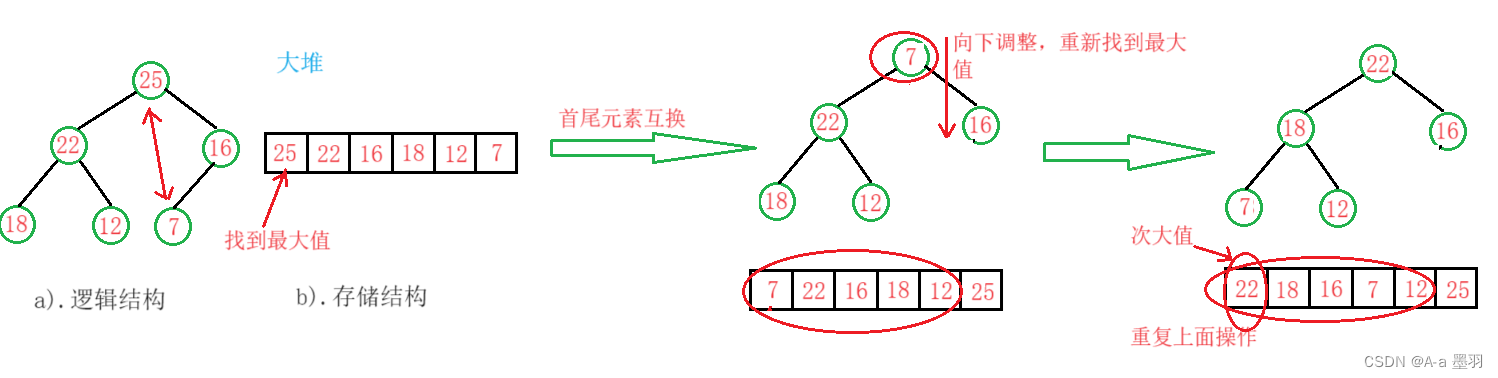
关于大/小堆的逻辑结构和存储结构如下:
由上图我们也可以观察出,虽然在大堆的逻辑结构中,每个父亲节点都要大于它的孩子节点,但在大堆的存储结构中并不是以完全的从大到小的顺序存储的,小堆亦然。
二、堆结构的实现
上面讲述了堆的存储结构结构为数组,那么我们可以像建顺序表那样来建堆,用int capacity来表示堆可存储的数据个数,int size表示当前已存储的数据个数·,HPDataType* a表示存储堆数据的数组。
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int capacity;//数组容量int size;//当前数据个数
}HP;
虽然堆的本质上是一个数组,但我们实现插入和删除操作时,是将其当作一个二叉树来调整的。对于如何标识逻辑结构下的堆的每个节点,因为已知根节点是数组中下标为0的元素,那么用各个节点所对应数组中元素的下标来标识节点(即将完全二叉树结构自第一层次向下依次遍历每一层次节点并计数)。基于此,用parent表示父亲节点,child表示其孩子节点,可以得到如下表达式parent = (child - 1) / 2;、child1(左) = parent * 2 + 1;、child2(右) = parent * 2 + 2。
下面各个函数是以建小堆为目的实现的。
2.1堆向下调整算法
能运用向下调整算法AdjustDown()的前提是,除根节点以外其余都以满足小堆的条件(即父亲节点小于各个孩子节点)。此函数需要三个参数:a表示需要调整的数组(堆),parent表示需要调整的那个节点的下标,size表示数组长度。
首先我们要找到此父亲节点的孩子节点,并假设左孩子小于右孩子(child = parent * 2 + 1)。然后比较左右孩子节点大小,取较小的那个作为新的孩子,还需要注意的是我们要新增判断(child + 1 < size)防止没有右孩子导致越界访问,最后比较父亲和孩子节点的大小,并更新父亲和孩子,直至child超出size范围(即再无孩子节点)。
逻辑大致如下:
//向下调整算法
void AdjustDown(HPDataType* a, int size, int parent)
{//假设判断int child = parent * 2 + 1;//调整if (child + 1 < size && a[child] > a[child + 1]){++child;}//交换while (child < size){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
2.2堆向上调整算法
同理,能运用向上调整算法AdjustUp()的前提是,除要插入节点的位置(即下标为size)以外其余都以满足小堆的条件(即父亲节点小于各个孩子节点)。与向下调整算法不同的是,AdustUp()只需要两个参数,一个为a表示需要调整的数组(堆),另一个为child表示所需调整节点的下标(即数组最后一个元素)。
与向下调整算法不同的是,向上调整不需要比较两个孩子的大小,因为其余节点已满足父亲节点大于孩子节点。于是乎,首先我们要找到父亲节点parent = (child - 1) / 2,然后比较父亲和孩子大小,若a[child] < a[parent]就交换,直到child值小于0或父亲节点大于孩子节点结束。
逻辑大致如下:
//堆向上调整
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//交换while (child > 0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
2.3删除堆顶元素
在堆结构中进行删除操作,一般会选择删除堆顶元素,但首先还要确保堆中有节点(断言assert(php->size > 0);),然后可以将最后一个元素(即下标为size - 1),移动到堆顶,并将size--,再进行向下调整算法。
逻辑大致如下:
//删除堆顶--根节点
void HeapPop(HP* php)
{assert(php);assert(php->size > 0);//首尾互换Swap(&php->a[0], &php->a[php->size - 1]);php->size--;//向下调整AdjustDown(php->a, php->size , 0);
}
2.4插入元素
在堆结构中进行插入操作,一般会选择堆尾。因为堆的底层是用数组实现的,且是需要动态开辟的。那么在每次插入元素之前都要先判断一下数组容量capacity,若size == capacity就需要扩容。最后只需要在完成插入操作后,对最后一个元素进行向上调整即可。
逻辑大致如下:
//插入元素
void HeapPush(HP* php, HPDataType x)
{assert(php);//判断容量if (php->size == php->capacity){size_t newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("HeapPush()::realloc");return;}php->a = tmp;php->capacity = newcapacity;}//插入php->a[php->size] = x;php->size++;//堆向上调整AdjustUp(php->a, php->size - 1);
}
2.5其他函数接口
- 判断堆是否为空:
php->size就代表堆中的有效的元素个数,那么当php->size == 0为真时就代表堆为空。
//为空判断
bool HeapEmpty(HP* php)
{assert(php);return php->size == 0;
}
- 返回堆顶元素:首先就要判断堆中是否有元素(断言即可
assert(php->size != 0)),若有则返回数组中下标为0的元素(即堆顶,根节点)。
//返回堆顶
HPDataType HeapTop(HP* php)
{assert(php);assert(php->size != 0);return php->a[0];
}
三、堆结构的应用
了解了堆结构的实现方法,我们便可以将其运用到以下两个问题中:
3.1堆排序
这里的堆排序是基于数组,运用二叉树的性质(即将待排序的数组当作一棵完全二叉树)来实现的,不会过多的动态开辟空间。 要与重新建堆的堆排序区别开(下面topk问题会用到,所以这里就不介绍了)!
如果我们要将此数组排成一个升序的数组,要如何实现呢?
既然此数组可当作一棵完全二叉树,那么首先我们就要将此树排成大堆,那么要建大堆而不建小堆呢?根据堆的性质,大堆的根节点可以筛选最大值,同理 小堆的根节点可以用来筛选最小值,那么如果我们建了小堆,就要 将最小值(即根节点)保留,然后将除此元素的数组的逻辑结构重新当作一个完全二叉树,那么这个二叉树的 各个节点间的关系就全都乱了,需要重新排成小堆。
由以上逻辑我们也可以看出,如果建小堆,那么此问题将变得十分复杂,且时间复杂度也很高。 既然这样,那么我们就可以建大堆来将数组排为升序:
我们用大堆找到最大值,然后将首尾元素互换,这样大堆的各个节点的关系就不会被打乱(不需要重新排大堆),最后只需要将堆顶的元素向下调整AdjustDown()重新找到次大值,需要注意的是调整时要将size-- 以避免已有最大值对此次调整造成影响,以此类推便得到一个升序数组。
那么我们要如何在一个数组上将其排为大堆呢?介绍以下两种方法:
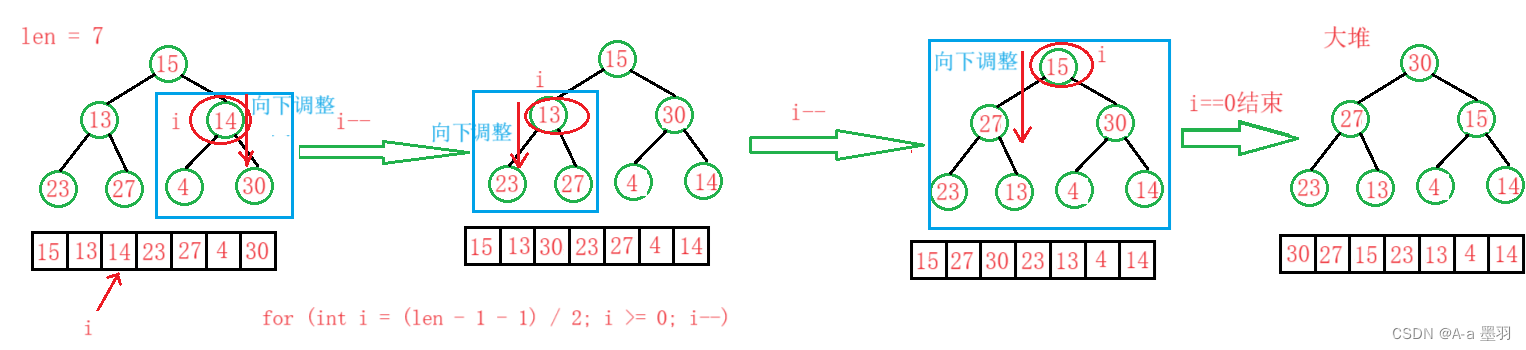
- 方法一:向下调整
给定一个数组,从下标为(len - 1 - 1) / 2的元素开始,直到下标为0,并将此值赋给parent。对下标为parent到len - 1之间的元素排大堆。(从后面元素开始向下调整)逻辑大致如下:
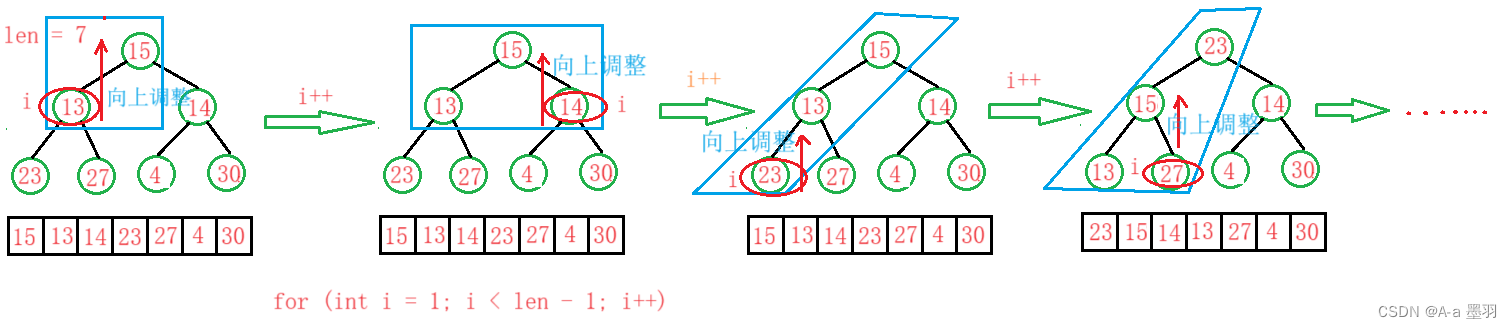
- 方法二:向上调整
与向下调整相似,我们可以从下标为1的元素开始,直到下标为len - 1,并将此值赋给child。对下标为0到child之间的元素排大堆。(从前面元素开始向上调整)逻辑大致如下:
那么两种方法谁更优呢?事实上方法一要优于方法二,这里就不多介绍了,只提供一下思路:方法一中我们所需要调整的节点个数相较于数组长度少一半(即少了二叉树最后一层次的调整),且越靠后的层次(节点数多)所需调整的步数越少;而方法二中我们所需要调整的节点个数与数组长度相近,且越靠后的层次(节点数多)所需要调整的步数越多。
那么虽然两种方法时间复杂度都为O(N*log(N)),但实际上方法一中调整次数要少于方法二。
// 对数组进行堆排序--从小到大
void HeapSort(int* a, int len)
{//方法二:--O(N*logN)/*for (int i = 1; i < len - 1; i++){AdjustUp(a, i);}*///方法一:--O(N*logN)for (int i = (len - 1 - 1) / 2; i >= 0; i--){AdjustDown(a, len - 1, i);}int end = len - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end-1, 0);end--;}
}
3.2Top-k问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
- 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆 - 用剩余的N-K个元素依次与堆顶元素来比较,满足则替换堆顶元素,并向下调整
为了模拟此问题,我们可以先造10000个整型放到文件中,要找最大值时再从文件中一个个读出。为了保证数据的随机性,我们可以使用srand()函数,并设置一个不断变化的时间戳(unsigned int)time(0)。 具体造数据方法如下:
//造数据
void CreatData()
{int n = 10000;srand((unsigned int)time(0));const char* fileName = "data.txt";FILE* file = fopen(fileName, "w");if (file == NULL){printf("fopen()::fail");exit(-1);}for(size_t i = 0; i < n; i++){int x = (rand() + i) % 10000;fprintf(file, "%d\n", x);}
}
既然此问题的目的是找出最大的k个数(k远小于数据个数),那么我们可以建一个只能存放k个数据的小堆。 估计会有以下两个疑问:
- 为什么只建能存放
k个数据的堆?
因为如果将文件中的所以数据都建成堆,那么当数据一多时,动态开辟内存将十分巨大,甚至会造成溢出问题。 且有一个数据插入时,堆都需要重新调整,这样一来时间复杂度将会很高,运行效率也大大降低。 - 为什么建小堆而不建大堆?
反过来想一下,如果建大堆的话,当最大的数已找到,那么它将一直堵在堆顶,其余的所有数都无法进堆。所以我们选择建小堆,堆顶元素最小,每当有新元素时只需要和堆顶进行比较即可,大的替换堆顶并向下调整,小的直接跳过即可。
代码实现如下:
//前k个大的数
void PrintTopK(int k)
{//建有五个数的堆--小堆FILE* file = fopen("data.txt", "r");if (file == NULL){printf("fopen()::fail");exit(-1);}int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc()::fail");exit(-1);}for (int i = 0; i < k; i++){fscanf(file, "%d", &minheap[i]);AdjustUp(minheap, i);}//将数据依次比较,大的下沉--向下调整int x;while (fscanf(file, "%d", &x) != EOF){if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}//打印堆for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}putchar('\n');//销毁堆free(minheap);minheap = NULL;
}
四、堆概念及结构相关题目
- 已知小根堆为
8,15,10,21,34,16,12,删除关键字8之后需重建堆,在此过程中,关键字之间的比较次
数是(C)。
A 1
B 2
C 3
D 4解: 由此结构可以推断出,逻辑结构的二叉树有三层,将
12移动到堆顶,然后向下调整,在调整过程中首先比较两个孩子节点找出较小的那个(第一次),然后比较孩子和父亲节点大小(第两次),因为满足条件所以交换(8来到右子树),因为此时并无右孩子所以省略左右孩子大小的比较,最后只需要比较一次孩子和父亲节点即可(第三次)。
- 最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是(
C)
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]解: 首尾互换,堆顶向下调整
- 下列关于向下调整算法的说法正确的是(
B)
A.构建堆的时候要对每个结点都执行一次
B.删除操作时要执行一次
C.插入操作时要执行一次
D.以上说法都不正确解: A: 建堆时,从每一个非叶子节点开始,倒着一直到根节点,都要执行一次向下调整算法。
B: 删除元素时,首先交换堆顶元素与堆中最后一个元素,对中有效元素个数减1,即删除了堆中最后一个元素,最后将堆顶元素向下调整
C: 插入操作需要执行向上调整算法。
相关文章:
【数据结构和算法】---二叉树(2)--堆的实现和应用
目录 一、堆的概念及结构二、堆结构的实现2.1堆向下调整算法2.2堆向上调整算法2.3删除堆顶元素2.4插入元素2.5其他函数接口 三、堆结构的应用3.1堆排序3.2Top-k问题 四、堆概念及结构相关题目 一、堆的概念及结构 如果有一个数字集合,并把它的所有元素按完全二叉树…...
【大模型实践】基于文心一言的对话模型设计
文心一言(英文名:ERNIE Bot)是百度全新一代知识增强大语言模型,文心大模型家族的新成员,能够与人对话互动、回答问题、协助创作,高效便捷地帮助人们获取信息、知识和灵感。文心一言从数万亿数据和数千亿知识…...

聊聊PowerJob的StoreStrategy
序 本文主要研究一下PowerJob的StoreStrategy StoreStrategy tech/powerjob/worker/common/constants/StoreStrategy.java Getter AllArgsConstructor public enum StoreStrategy {DISK("磁盘"),MEMORY("内存");private final String des; }StoreStra…...

HTML+CSS+JS网页设计期末课程大作业 web课程设计 web前端开发 网页规划与设计
HTMLCSSJS网页设计期末课程大作业 web前端开发技术 web课程设计 网页规划与设计 💥 文章目录一、🚩 网站描述二、🎌 网站介绍三、🏴 网站类型A 个人博客主题B 人物明星主题C 旅游主题D 游戏主题E 动漫主题F 美食主题G 校园主题H 企…...

vscode | python | remote-SSH | Debug 配置 + CLIP4Clip实验记录
安装Extension 本地安装Remote-SSH、python 远程服务器上安装Python 难点:主机和远程服务器上安装Python扩展失败,可能是网络、代理等原因导致解决方法: 主机在官方网站下载Python扩展:https://marketplace.visualstudio.com/it…...

【Linux】实现windows主机与ubuntu虚拟机系统之间文件/字符复制粘贴
环境 硬件:通用PC 系统:Ubuntu 18.04 《 》Windows10 软件 :VMware Workstation 16 Pro 解决 0、现象 使用Ubuntu 虚拟机时,有时需要来回复制文件或者字符串到主机或虚拟机。 1、分析 2、思路 3、解决 //先安装open-vm-to…...

Ubuntu22.04-安装后Terminal无法调出
参考: Ubuntu20.04 终端打开不了的问题排查_ubuntu终端打不开-CSDN博客 https://blog.csdn.net/u010092716/article/details/130968032 Ubuntu修改locale从而修改语言环境_ubuntu locale-CSDN博客 https://blog.csdn.net/aa1209551258/article/details/81745394 问…...
ffmpeg两种windows版本区别说明
版本一 必须拷贝exe和dll文件才能使用,如果缺少dll则exe不正正常执行 如果缺少dll ,执行 exe会报错如下 版本2 直接拷贝exe就能使用,没有依赖的环境...

最新国内AI绘画Midjourney绘画提示词Prompt分享
一、Midjourney绘画工具 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭…...
ChatGPT4.0(中文版)国内无限制免费版(附网址)
ChatGPT,由OpenAI开发的人工智能语言模型。它是你的数字对话伙伴,无论你有何问题或需要什么帮助,它都能提供有用的信息。 经过不断的研发和更新,ChatGPT的性能和功能得到了显著提升。现在,我们将重点介绍ChatGPT的两个…...

模拟电路基础知识笔记,你想知道的都有,建议收藏!
大家总说模电知识总是学不会,IC修真院为大家整理了模拟电子基础知识,看看你掌握了多少,文末可以获取全部哦。 文末可领全部文档 1、PN结是晶体二极管的基本结构,也是一般半导体器件的核心。 2、 射极输出器没有电压放大能力&am…...
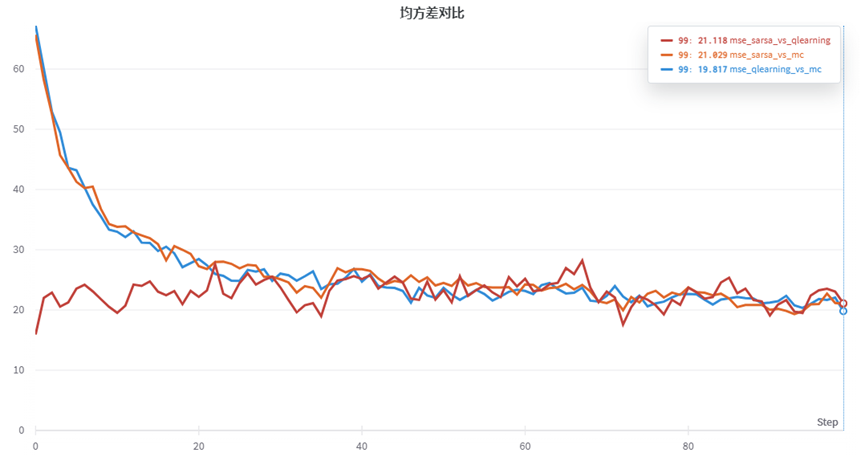
【强化学习】基于蒙特卡洛MC与时序差分TD的简易21点游戏应用
1. 本文将强化学习方法(MC、Sarsa、Q learning)应用于“S21点的简单纸牌游戏”。 类似于Sutton和Barto的21点游戏示例,但请注意,纸牌游戏的规则是不同且非标准的。 2. 为方便描述,过程使用代码截图,文末附链…...

Pandas 高级教程——高级时间序列分析
Python Pandas 高级教程:高级时间序列分析 Pandas 提供了强大的时间序列处理功能,使得对时间序列数据进行高级分析变得更加灵活和方便。在本篇博客中,我们将深入介绍 Pandas 中的高级时间序列分析技术,并通过实例演示如何应用这些…...
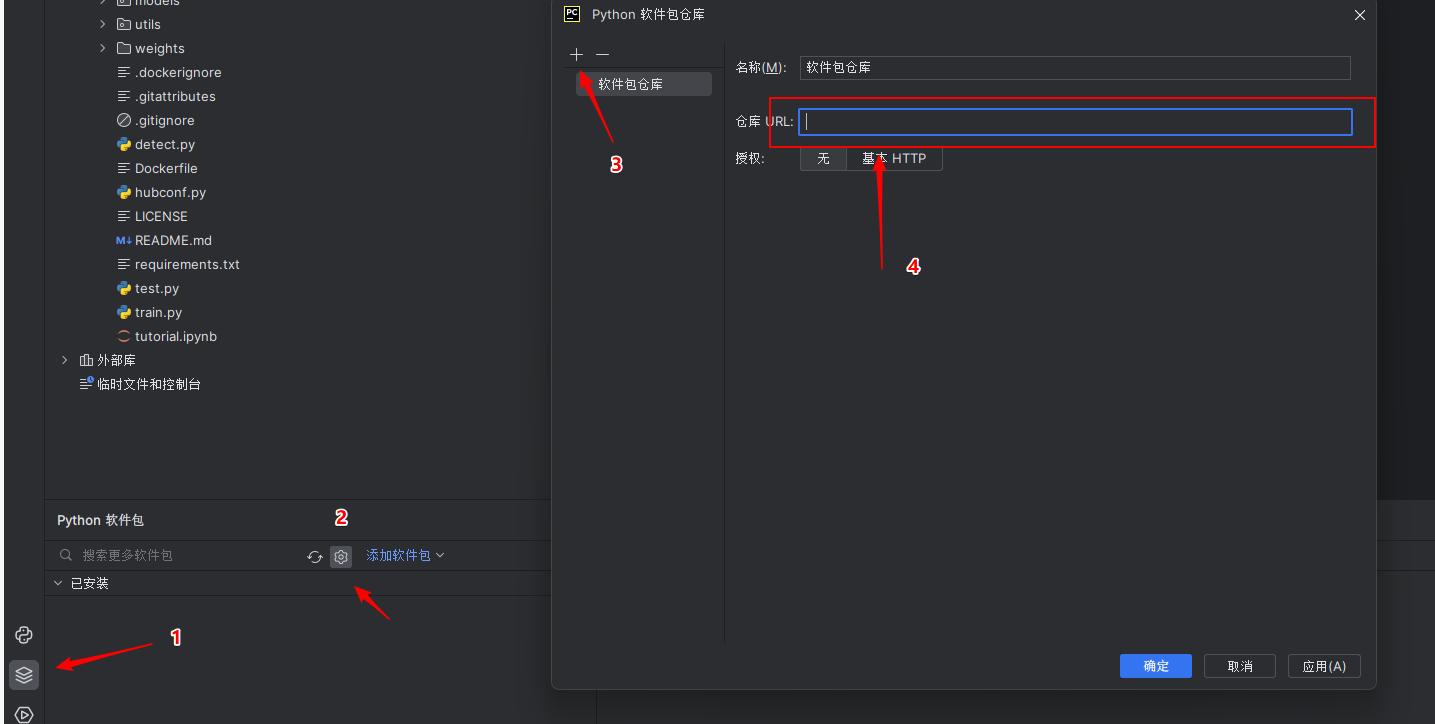
解决Pycharm pip安装模块太慢问题,pycharm2022没有manage repositories配置镜像源
解决方案 方法清华阿里云中国科技大学华中理工大学 或者直接-i 加镜像 方法 URL写下面任意一个 清华 https://pypi.tuna.tsinghua.edu.cn/simple阿里云 http://mirrors.aliyun.com/pypi/simple/中国科技大学 https://pypi.mirrors.ustc.edu.cn/simple/华中理工大学 http:/…...
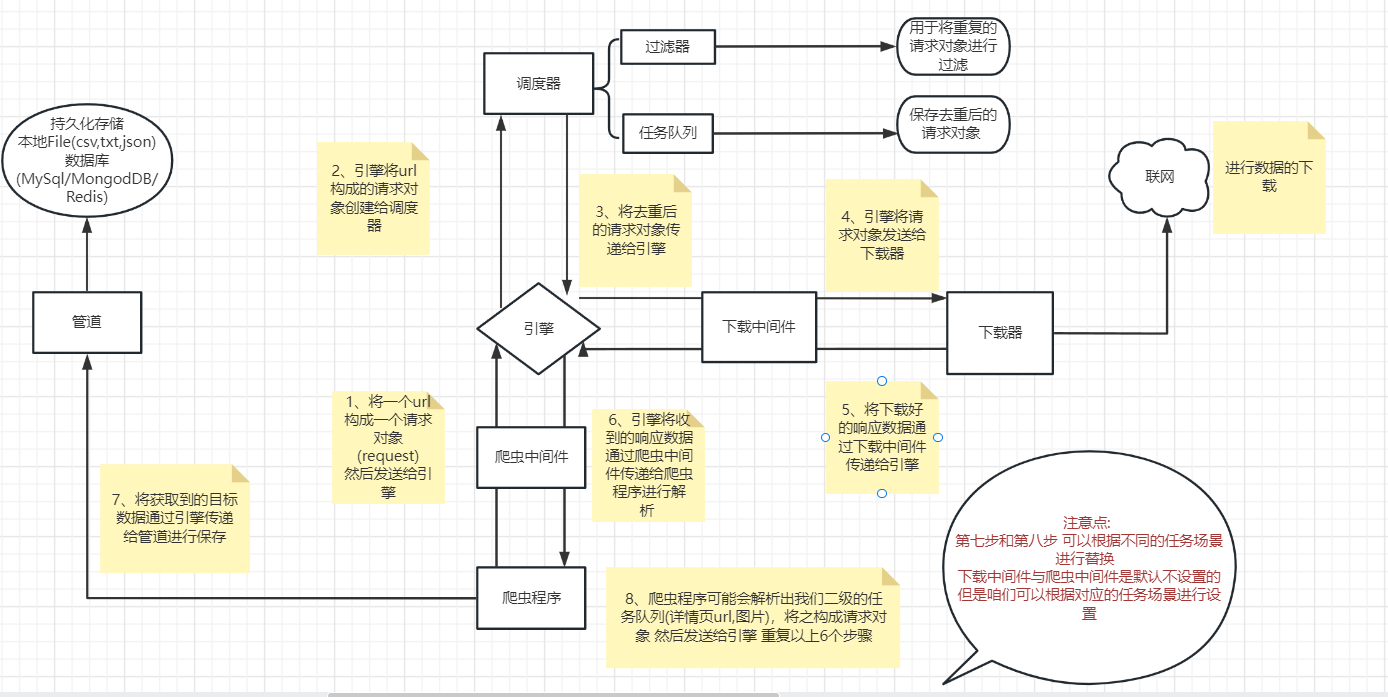
十二:爬虫-Scrapy框架(上)
一:Scrapy介绍 1.Scrapy是什么? Scrapy 是用 Python 实现的一个为了爬取网站数据、提取结构性数据而编写的应用框架(异步爬虫框架) 通常我们可以很简单的通过 Scrapy 框架实现一个爬虫,抓取指定网站的内容或图片 Scrapy使用了Twisted异步网…...
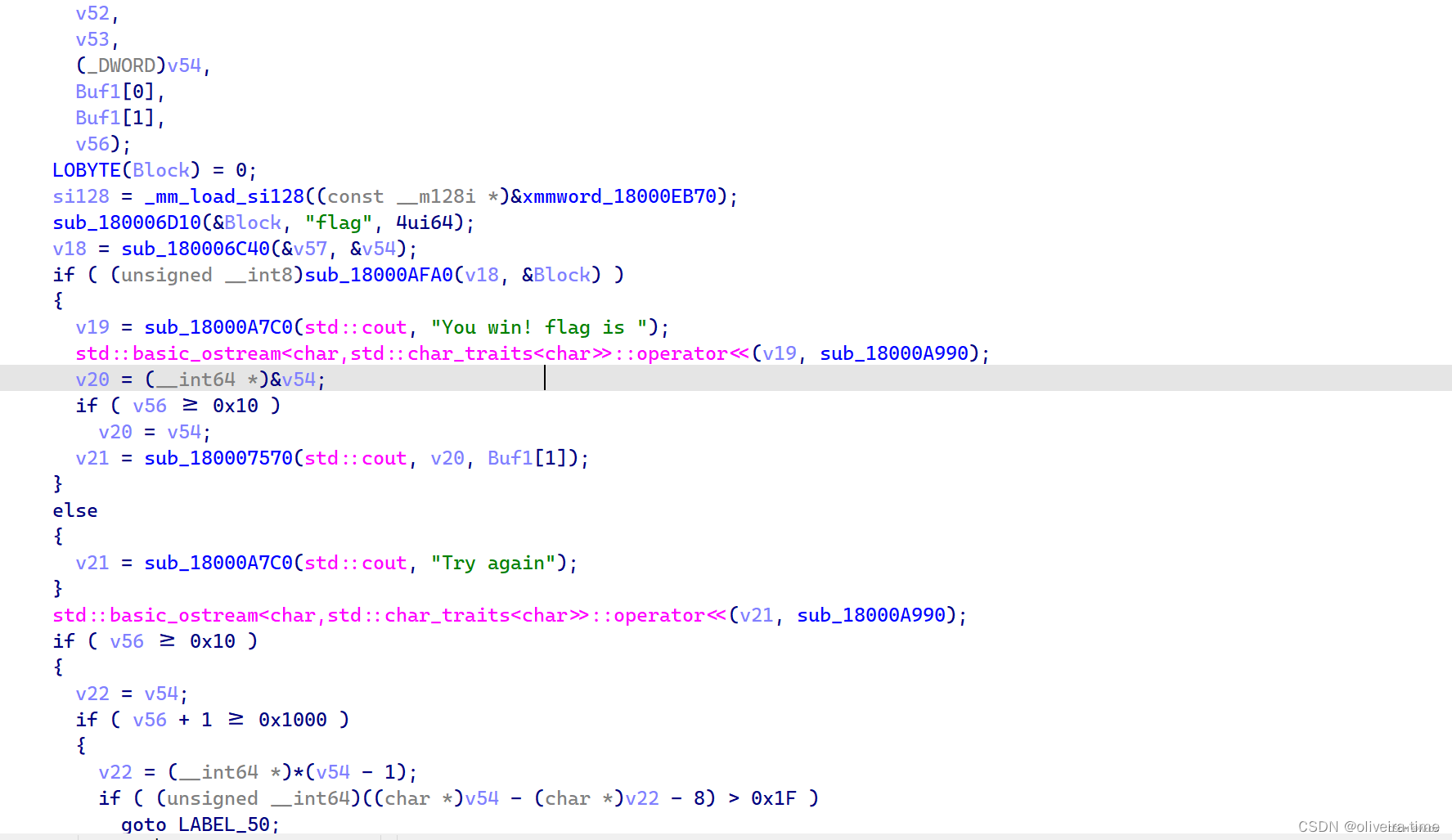
BUUCTF Reverse/[2019红帽杯]Snake
BUUCTF Reverse/[2019红帽杯]Snake 下载解压缩后得到可执行文件,而且有一个unity的应用程序,应该是用unity编写的游戏 打开是一个贪吃蛇游戏 用.NET Reflector打开Assembly-CSharp.dll。(unity在打包后,会将所有的代码打进一个Ass…...

概率论相关题型
文章目录 概率论的基本概念放杯子问题条件概率与重要公式的结合独立的运用 随机变量以及分布离散随机变量的分布函数特点连续随机变量的分布函数在某一点的值为0正态分布标准化随机变量函数的分布 多维随机变量以及分布条件概率max 与 min 函数的相关计算二维随机变量二维随机变…...

C#中的Attribute详解(上)
C#中的Attribute详解(上) 一、Attribute是什么二、Attribute的作用三、Attribute与注释的区别四、系统Attribute范例1、如果不使用Attribute,为了区分这四类静态方法,我们只能通过注释来说明,但这样做会给系统带来很多…...

天津医科大学临床医学院专升本药学专业有机化学考试大纲
天津医科大学临床医学院高职升本科专业课考试大纲药学专业《有机化学》科目考试大纲 一、考试基本要求 本考试大纲主要要求考生对《有机化学》基本概念有较深入的了解,能够系统地掌握各类化合物的命名、结构特点及立体异构、主要性质、反应、来源和合成制备方法等…...
电脑开机自动断电,简单4招,快速解决!
“不知道我的电脑最近是怎么回事,每次一开机就会出现自动断电的情况,有什么方法可以解决吗?” 在使用电脑时,由于电源供应不稳定或过热,以及各种硬件问题,可能会导致电脑开机自动断电。遇到这种情况&#x…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...