雨课堂作业整理
第一次作业
1.下列序列是图序列的是( )
A.1,2,2,3,4,4,5
B.1,1,2,2,4,6,6
C.0,0,2,3,4,4,5
D.2,2,2,2,2,2,2
2.具有3个顶点互不同构的图有( )个
A.4 B.3 C.2 D.1
3.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则 d ( v 1 ) = () d(v_1)=( ) d(v1)=()
A.4 B.3 C.2 D.1
4.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则顶点导出子图 G [ { v 1 , v 2 , v 3 } ] G[\{v_1,v_2,v_3\}] G[{v1,v2,v3}] 中有( )条边
A.5 B.4 C.3 D.2
5.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则边导出子图 G [ { v 1 v 1 , v 2 v 4 } ] G[\{v_1v_1,v_2v_4\}] G[{v1v1,v2v4}] 是图 G G G 的支撑子图。该说法( )。
A.正确 B.错误
6.若图 G G G 存在 ( u , v ) (u,v) (u,v) 闭途径,则图 G G G 中也一定存在 ( u , v ) (u,v) (u,v) 闭迹。该说法( )。
A.正确 B.错误
7.互不同构的 4 4 4 阶连通图有( )个。
A.6 B.5 C.4 D.3
8.在一个化学实验室里,有 n n n 个药箱,其中每两个不同的药箱恰有一种相同的化学品,而且每种化学品恰好在两个药箱中出现,则每个药箱有( )种化学品;这 n n n 个药箱种共有( )种不同的化学品。
9.平面上有 n n n 个点 S = { p 1 , p 2 , . . . , p n } S=\{p_1,p_2,...,p_n\} S={p1,p2,...,pn},其中任何两个点之间的距离至少是 1 1 1,证明这 n n n 个点中距离为 1 1 1 的点对数不超过 3 n 3n 3n。
证明:
第二次作业
1.每对顶点都相邻的图是完全图。该说法( )。
A.正确 B.错误
2.(多选)设聚会有 n n n 人参加,已知聚会中要么有 3 3 3 个人互相都认识,要么有 3 3 3 个人相互都不认识,则参与这次聚会的人数 n n n 可能是( )。
A.7 B.6 C.5 D.4
3.如下图 G G G 是著名的 P e t e r s e n Petersen Petersen 图,关于此图说法正确的是( )。

A.它是二部图 B.它不是二部图
4.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 , v 4 } , A = { ( v 1 , v 2 ) , ( v 3 , v 4 ) , ( v 1 , v 1 ) , ( v 2 , v 4 ) , ( v 3 , v 4 ) } V=\{v_1,v_2,v_3,v_4\},A=\{(v_1,v_2),(v_3,v_4),(v_1,v_1),(v_2,v_4),(v_3,v_4)\} V={v1,v2,v3,v4},A={(v1,v2),(v3,v4),(v1,v1),(v2,v4),(v3,v4)},则 d + ( v 1 ) = d^+(v_1)= d+(v1)=( )
A.4 B.3 C.2 D.1
5.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 , v 4 } , A = { ( v 1 , v 2 ) , ( v 3 , v 4 ) , ( v 1 , v 1 ) , ( v 2 , v 4 ) , ( v 3 , v 4 ) } V=\{v_1,v_2,v_3,v_4\},A=\{(v_1,v_2),(v_3,v_4),(v_1,v_1),(v_2,v_4),(v_3,v_4)\} V={v1,v2,v3,v4},A={(v1,v2),(v3,v4),(v1,v1),(v2,v4),(v3,v4)},则它有( )个强连通分支。
A.4 B.3 C.2 D.1
6.任何长为奇数的闭途径中一定包含长为奇数的圈。该说法( )。
A.正确 B.错误
7.某次聚会很特别,在这次聚会中,每两个互相认识的人,都没有共同的熟人,但,每两个互不认识的人都恰有两个共同的熟人。有人宣称这次聚会的参加者一定有同样数目的熟人他的说法( )
A.正确 B.错误
8.完全二部图 K m , n K_{m,n} Km,n中有( )条边。
9.构造一个 7 7 7 阶 4 4 4 正则简单图。
第三次作业
1.设 A ( G ) = A(G)= A(G)=
( 1 2 0 2 2 1 0 1 3 ) (3) \begin{pmatrix} 1 & 2 & 0 \\ 2 & 2 & 1 \\ 0 & 1 & 3 \end{pmatrix} \tag{3} 120221013 (3),则顶点 v 1 v_1 v1 的度 d ( v 1 ) = d(v_1)= d(v1)=
A.5 B.4 C.3
2.设 A ( G ) = A(G)= A(G)=
( 1 2 0 2 2 1 0 1 3 ) (3) \begin{pmatrix} 1 & 2 & 0 \\ 2 & 2 & 1 \\ 0 & 1 & 3 \end{pmatrix} \tag{3} 120221013 (3),则顶点 v 2 v_2 v2 到 v 2 v_2 v2 且长为 2 2 2 的不同路径有( )条。
A.9 B.8 C.7 D.6
3.设 A ( G ) = A(G)= A(G)=
( 0 0 1 2 1 1 1 3 0 ) (3) \begin{pmatrix} 0 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 3 & 0 \end{pmatrix} \tag{3} 021013110 (3),则有向图 D D D 中的有向边 ( v 2 , v 3 ) (v_2,v_3) (v2,v3) 有( )条。
A.3 B.2 C.1 D.0
4.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 } , A = { ( v 1 , v 2 ) , ( v 1 , v 3 ) , ( v 2 , v 3 ) , ( v 3 , v 2 ) } V=\{v_1,v_2,v_3\},A=\{(v_1,v_2),(v_1,v_3),(v_2,v_3),(v_3,v_2)\} V={v1,v2,v3},A={(v1,v2),(v1,v3),(v2,v3),(v3,v2)},则关联矩阵 M ( D ) = M(D)= M(D)=( )
A. [ 1 1 0 0 − 1 0 1 − 1 0 − 1 − 1 1 ] \begin{bmatrix} 1 & 1 & 0 & 0 \\ -1 & 0 & 1 & -1 \\ 0 & -1 & -1 & 1 \end{bmatrix} 1−1010−101−10−11
B. [ − 1 − 1 0 0 1 0 − 1 1 0 1 1 − 1 ] \begin{bmatrix} -1 & -1 & 0 & 0 \\ 1 & 0 & -1 & 1 \\ 0 & 1 & 1 & -1 \end{bmatrix} −110−1010−1101−1
C. [ 1 1 0 0 1 0 1 1 0 1 1 1 ] \begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \end{bmatrix} 110101011011
5.设 G G G 如下图所示,则 ε ( G − v ) = \varepsilon(G-v)= ε(G−v)= ( )

A.8 B.6 C.4 D.2
6.设 G 1 , G 2 G_1,G_2 G1,G2 分别如下图所示,则 v ( G 1 ∪ G 2 ) = v(G_1 \cup G_2)= v(G1∪G2)=( )

A.5 B.4 C.3 D.2
7.设 G G G 如下图所示,则 G ⋅ e G·e G⋅e 的基础简单图有( )条边。

A.11 B.10 C.9 D.8
8.求下图 v 1 v_1 v1 到 v 2 v_2 v2 的最短路( )。

9.判断下图能否转化为笛卡尔积的形式,简述理由。

第四次作业
1.互不同构的六阶树有( )个。
A.10 B.8 C.6 D.4
2.已知 G G G 为简单图,且 v ( G ) = ε ( G ) = 2023 v(G)=\varepsilon(G)=2023 v(G)=ε(G)=2023,下列说法正确的是( )。
A. G G G 中一定有圈
B. G G G 一定连通
C. G G G 中不一定有圈
D. G G G 不一定联通
3.(多选)下列选项中有可能是树图的度序列的有 ()
A.(1,2,2,2,2,3)
B.(0,1,1,2,3,3)
C.(1,1,1,2,2,3)
D.(1,1,1,1,2,4)
4.(多选)设 G G G 是连通图, e ∈ E ( G ) e \in E(G) e∈E(G),则 w ( G − e ) w(G -e) w(G−e) 可能是( )
A.1 B.2 C.3 D.4
5.设图 G G G 有 v v v 个顶点、 ε \varepsilon ε 条边和 ω \omega ω 个连通分支, G G G 中不同圈的个数为 n n n,则下列关于 n n n 的说法最恰当的是( )。
A. n ≥ ε − v n \geq \varepsilon-v n≥ε−v
B. n ≥ ε − v + ω n \geq \varepsilon-v+\omega n≥ε−v+ω
C. n ≤ ε − v − ω n \leq \varepsilon-v-\omega n≤ε−v−ω
D. n ≤ v − ω n \leq v-\omega n≤v−ω
6.设 G G G 如下图所示,则 τ ( G ) = \tau(G)= τ(G)=( )。

A.8 B.6 C.5 D.4
7. τ ( K 5 ) = \tau(K_5)= τ(K5)=( )。
A. 5 10 5^{10} 510 B. 5 8 5^8 58 C. 5 5 5^5 55 D. 5 3 5^3 53
8.设 G G G 如下图所示,则 G G G 中含有边 e e e 的支撑树有( )。

9.设 T T T 是一棵树,其平均度为 α \alpha α,求 v ( T ) v(T) v(T)。
相关文章:

雨课堂作业整理
第一次作业 1.下列序列是图序列的是( ) A.1,2,2,3,4,4,5 B.1,1,2,2,4,6,6 C.0,0,2&am…...

C#/WPF 只允许一个实例程序运行并将已运行程序置顶
使用用互斥量(System.Threading.Mutex): 同步基元,它只向一个线程授予对共享资源的独占访问权。在程序启动时候,请求一个互斥体,如果能获取对指定互斥的访问权,就职运行一个实例。 实例代码: /// <…...
【基础】【Python网络爬虫】【1.认识爬虫】什么是爬虫,爬虫分类,爬虫可以做什么
Python网络爬虫基础 认识爬虫1.什么是爬虫2.爬虫可以做什么3.为什么用 Ptyhon 爬虫4.爬虫的分类通用爬虫聚焦爬虫功能爬虫增量式爬虫分布式爬虫 5.爬虫的矛与盾(重点)6.盗亦有道的君子协议robots7.爬虫合法性探究 认识爬虫 1.什么是爬虫 网络爬虫&…...
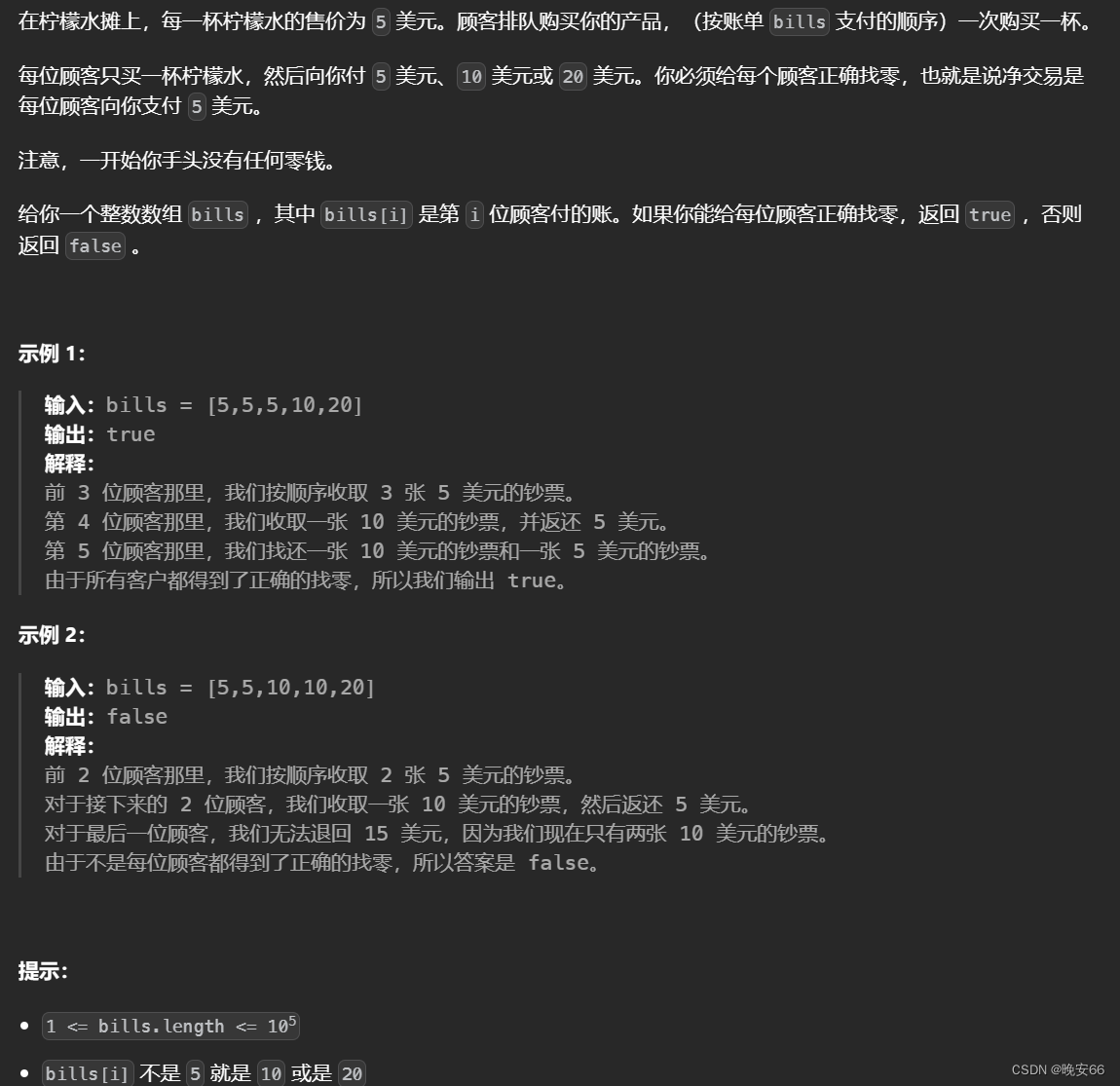
【算法与数据结构】860、LeetCode柠檬水找零
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题的思路比较简单,首先要保存收到的零钱,其次计算找零,最后分解找…...

「Verilog学习笔记」乘法与位运算
专栏前言 本专栏的内容主要是记录本人学习Verilog过程中的一些知识点,刷题网站用的是牛客网 观察乘数的特点: 1111_1011 1_0000_0000 - 1 - 100 timescale 1ns/1nsmodule dajiang13(input [7:0] A,output [15:0] B);//*************code*********…...

CSS与JavaScript的简单认识
CSS:是一门语言,用于控制网页表现,让页面更好看的。 CSS(Cascading Style Sheet):层叠样式表 CSS与html结合的三种方式: 1、内部样式:用style标签,在标签内部定义CSS样式…...
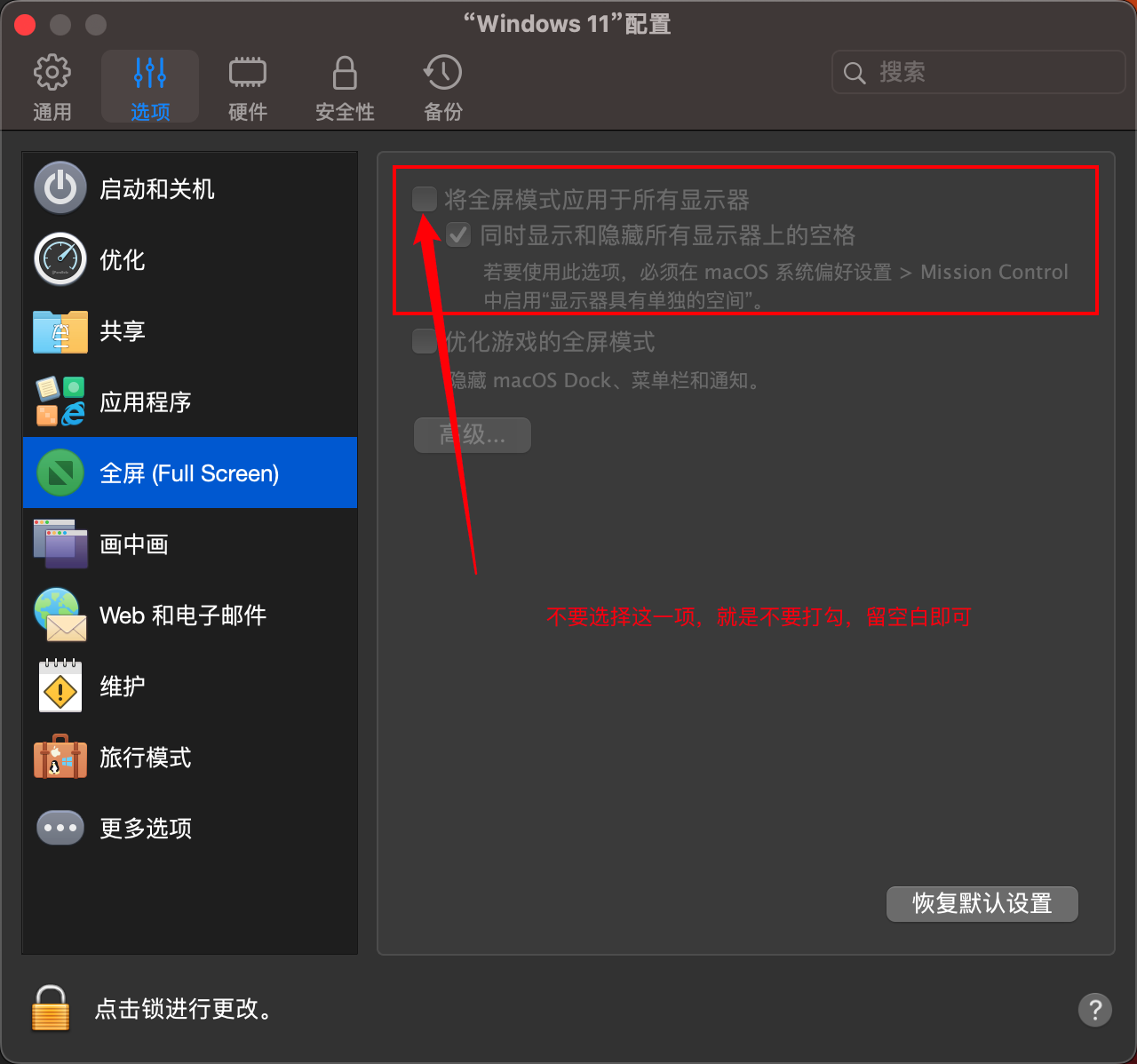
MAC 中多显示器的设置(Parallels Desktop)
目录 一、硬件列表: 二、线路连接: 三、软件设置: 1. 设置显示器排列位置及显示参数 2. 分别设置外接显示器为:扩展显示器,内建显示器为主显示器 3. 设置Parallels Desktop屏幕参数 四、结果 一、硬件列表&a…...

迁移到云原生:如何使用微服务迁移应用程序
企业遇到大规模部署和监督生产中的应用程序的任务。幸运的是,我们可以使用大量技术和工具。然而,从传统的,整体的结构转变为云态一个人提出了自己的障碍。在这里,您会发现将应用程序从整体设置转移到基于微服务的体系结构时要进行…...
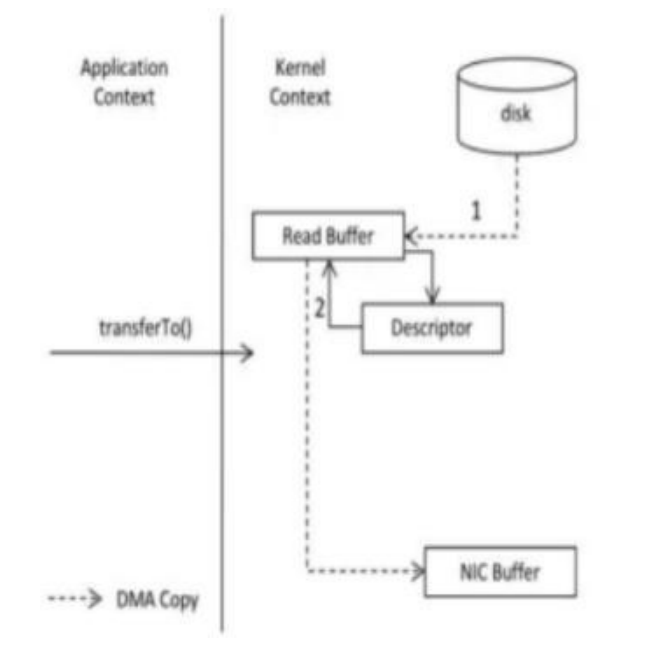
kafka 的零拷贝原理
文章目录 kafka 的零拷贝原理 今天来跟大家聊聊kafka的零拷贝原理是什么? kafka 的零拷贝原理 零拷贝是一种减少数据拷贝的机制,能够有效提升数据的效率; 在实际应用中,如果我们需要把磁盘中的某个文件内容发送到远程服务器上…...
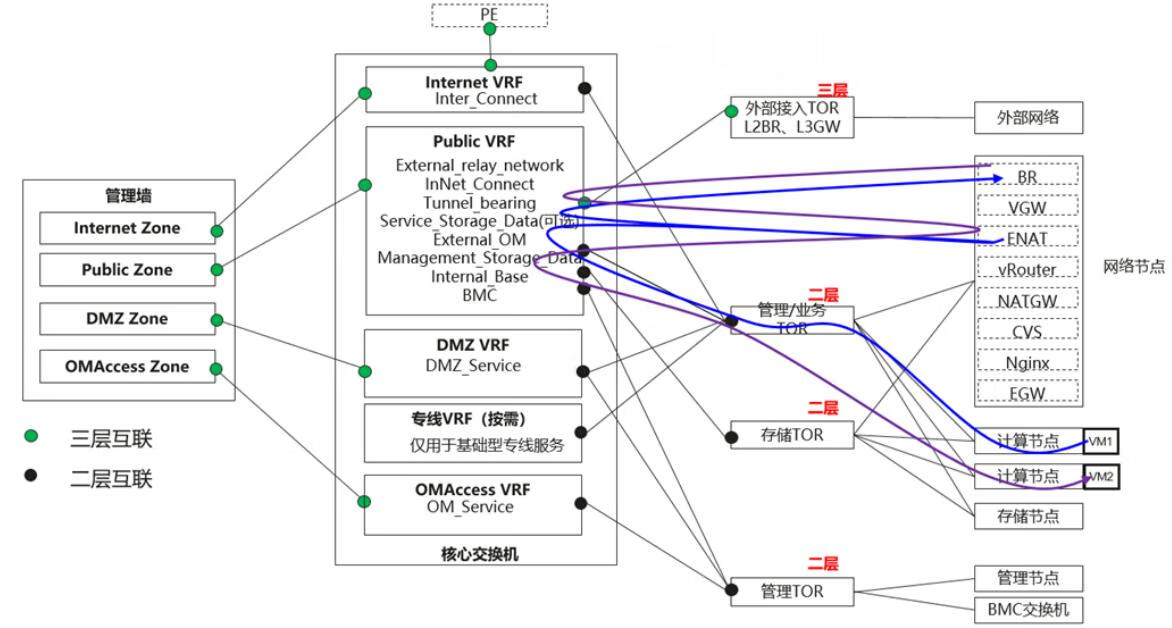
华为云Stack 8.X流量模型分析(五)
六、EIP流量模型分析 弹性公网IP(Elastic IP,简称EIP)提供独立的公网IP资源,包括公网IP地址与公网出口带宽服务。如果资源只配置了私网IP,则无法直接访问Internet,为资源配置弹性公网IP后,可…...

学习动态规划解决不同路径、最小路径和、打家劫舍、打家劫舍iii
学习动态规划|不同路径、最小路径和、打家劫舍、打家劫舍iii 62 不同路径 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量dp[i][j] dp[i-1][j] dp[i][j-1] import java.util.Arrays;/*** 路径数量* 动态规划,dp[i][j]表示从左上角到(i,j)的路径数量…...

nodejs微信小程序+python+PHP特困救助供养信息管理系统-计算机毕业设计推荐
目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性:…...

Vue(二):计算属性与 watch 监听器
03. Vue 指令拓展 3.1 指令修饰符 可以通过 . 来指明一些指令的后缀,不同的后缀中封装了不同的操作,可以帮助我们简化代码,比如之前使用过的监听 enter 键的弹起,我们需要操作事件对象,来检测用户使用了哪个键&#…...

25、WEB攻防——通用漏洞SQL读写注入MYSQLMSSQLPostgreSQL
文章目录 Mysql-root高权限读写注入PostgreSQL——dba高权限读写注入Mssql-sa高权限读写注入 Access无高权限注入点——只能猜解,而且是暴力猜解; MYSQL,PostgreSQL,MSSQL(SQL server)高权限注入点——可升级读写(文件…...

【第5期】前端Vue使用Proxy+Vuex(store、mutations、actions)跨域调通本地后端接口
本期简介 本期要点 本地开发前后端如何跨域调用全局请求、响应处理拦截器处理封装HTTP请求模块编写API请求映射到后端API数据的状态管理 一、 本地开发前后端如何跨域调用 众所周知,只要前端和后端的域名或端口不一样,就存在跨域访问,例如&…...
编译器中,Release和Debug区别)
在Visual Studio(VS)编译器中,Release和Debug区别
一、 优化级别 1、Debug(调试) 在Debug模式下,编译器不会对代码进行优化,而是专注于生成易于调试的代码。这使得开发者可以在调试过程中更直观地跟踪变量的值和程序的执行流程。 2、Release(发布) 在Relea…...
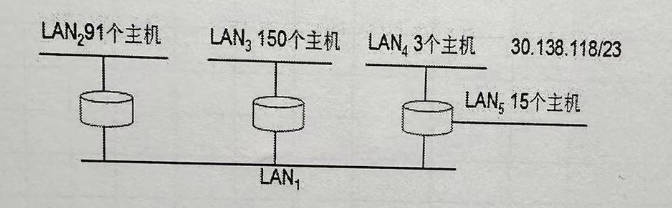
子网划分问题(实战超详解)_主机分配地址
文章目录: 子网划分的核心思想 第一步,考虑借几位作为子网号 第二步,确定子网的网络地址 第三步,明确网络地址,广播地址,可用IP地址范围 一些可能出现的疑问 实战 题目一 子网划分的核心思想 网络号不变,借用主机号来产生新的网络 划分前的网络:网络号主机号 划分后的网络:原网…...

【QT】单例模式,Q_GLOBAL_STATIC 宏的使用和使用静态成员函数,eg:{简单的日志记录器}
简单的日志记录器为例 。 创建一个Logger类,该类负责记录应用程序的日志消息 使用 Q_GLOBAL_STATIC 宏 解析:Q_GLOBAL_STATIC 是一个 Qt 宏,用于创建全局静态实例。它确保在需要时只创建一次实例,而不管该实例是在哪个线程中创建…...

利用小红书笔记详情API:构建高效的内容创作与运营体系
随着社交媒体的兴起,小红书作为国内知名的内容分享平台,吸引了大量用户和内容创作者。为了更好地获取小红书上的优质内容,许多企业和开发者选择使用小红书笔记详情API。本文将探讨如何利用该API构建高效的内容创作与运营体系。 一、小红书笔记…...
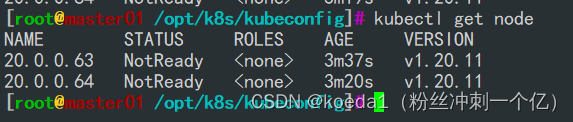
【K8S 二进制部署】部署单Master Kurbernetes集群
目录 一、基本架构和系统初始化 1、集群架构: 2、操作系统初始化配置: 2.1、关闭防火墙和安全机制: 2.2、关闭swap 2.3、根据规划设置主机名 2.4、三台主机全部互相映射 2.5、调整内核参数 3、时间同步(所有节点时间必须同…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
