当前位置： 首页 > news >正文

小秋SLAM入门实战opencv所有文章汇总

news 文章来源：https://blog.csdn.net/qq_21950671/article/details/135297368 2024/10/30 21:31:42

opencv_core和 opencv_imgcodecs是 OpenCV（开源计算机视觉库）的两个主要模块
【如何使用cv::erode()函数对图像进行腐蚀操作】
头文件用途
用OpenCV创建一张类型为CV_8UC1的单通道随机灰度图像
用OpenCV创建一张灰度黑色图像并设置某一列为白色
OpenCV创建一张类型为CV_8UC3的3通道彩色图像
OpenCV创建一张类型为CV_8UC4的4通道图像
OpenCV读取一张8位无符号单通道图像并显示
OpenCV读取一张8位无符号三通道图像并显示
OpenCV读取一张8位无符号四通道图像并显示
OpenCV读取一张深度图像并显示
OpenCV读取两张图像将下半部分（从中间行开始）的所有像素值设置为0黑色
OpenCV通过ptr＜uchar＞(y)获取第y行的首地址，通过data[x]获取第x列的像素值遍历单通道像素
OpenCV通过ptr＜uchar＞(y)获取第y行的首地址，通过data[x]获取第x列的像素值遍历三通道像素
OpenCV库中图像的基本处理方法和一些重要的概念
OpenCV实现一张图片的特定区域上添加另一张图片
OpenCV在一张图片上以不同的透明度添加另一张图片
OpenCV图像的仿射变换、旋转和缩放
OpenCV在一个图像上画一个空心绿色的圆和一个实心红色的圆
OpenCV使用ellipse()函数来绘制一个椭圆
OpenCV红色图像上用绿色画了两条线
OpenCV使用clone()函数来进行深度拷贝，拷贝后的image_clone修改不会影响原始图像image
OpenCV绘制矩形
OpenCV的remap实现图像垂直翻转
OpenCV 的 remap 函数改变图像中像素的位置
图像文件重命名
OpenCV对图片进行缩放处理
OpenCV使用pyrUp对图片进行放大处理
OpenCV图像金字塔pyrDown下采样
OpenCV库实现了一个简单的图像放缩工具
OpenCV库进行图像旋转、仿射变换和透视变换
OpenCV使用putText将文字绘制到图像上
使用OpenCV的viz模块创建和控制一个3D可视化窗口
使用OpenCV检测两张图片的关键点并计算关键点的描述子
使用OpenCV显示图像的RGB颜色直方图
使用OpenCV在图像上绘制质心
如何安装 OpenCV 和 OpenCV_contrib
#include＜opencv2/core/core.hpp＞头文件的用途
image_transport
如何计算一张图像占据多少内存
【OpenGL】
feature_tracker、goodFeaturesToTrack、calcOpticalFlowPyrLK、findFundamentalMat、findEssentialMat
「Ubuntu&ROS」Ubuntu系统OpenCV多版本共存和使用教程
【OpenCV】图像的形态学操作｜腐蚀｜膨胀｜Canny边缘检测
【OpenCV】图像旋转 平移 仿射变换 透视变换
【OpenCV】图像多通道混合、缩放
【OpenCV】图像上画线、文字、椭圆、矩形框
【OpenCV】图像批量重命名
【OpenCV】图像的像素直方图 图像特征点 cv::FAST cv::ORB ORB_SLAM2::ORB
【OpenCV】模拟图像 数字图像 光心 基线
【OpenCV】创建图像 像素遍历 像素显示 Vec4b Vec3b ptr at uchar
【OpenCV】图像添加噪声 GaussianBlur medianBlur bilateralFilter
【OpenCV】图像去畸变

相关文章：

小秋SLAM入门实战opencv所有文章汇总

opencv_core和 opencv_imgcodecs是 OpenCV（开源计算机视觉库）的两个主要模块 【如何使用cv::erode()函数对图像进行腐蚀操作】 头文件用途 用OpenCV创建一张类型为CV_8UC1的单通道随机灰度图像 用OpenCV创建一张灰度黑色图像并设置某一列为白色 OpenCV创…...

编程日记 2024/1/5 20:13:01

2023年终总结（脚踏实地，仰望星空）

回忆录 2023年，经历非常多的大事情，找工作、实习、研究生毕业、堂哥结婚、大姐买车、申博、读博、参加马拉松，有幸这一年全家人平平安安，在稳步前进。算是折腾的一年，杭州、赣州、武汉、澳门、珠海、遵义来回跑。完成…...

编程日记 2024/1/5 20:10:59

Transforer逐模块讲解

本文将按照transformer的结构图依次对各个模块进行讲解： 可以看一下模型的大致结构：主要有encode和decode两大部分组成，数据经过词embedding以及位置embedding得到encode的时输入数据 输入部分 embedding就是从原始数据中提取出单词或位置&…...

编程日记 2024/1/5 20:07:57

macOS进程间通信的常用技术汇总

macOS进程间通信的常用技术汇总 命令行传参。yyds管道(pipe), 匿名管道， c的技术，可以跨平台使用 只能在父子进程间通信，由于是单向的管道，只能单方面传输数据。 如果需要双向传输，需要建立双向的两条管道才行 匿名管…...

编程日记 2024/1/5 20:06:56

高德地图信息窗体设置

1. 添加默认信息窗体 //构建信息窗体中显示的内容var info [];info.push(<div style"height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置&#xff1a;北京</div>);info.push(<div style"height: 36px; line-heig…...

编程日记 2024/1/5 20:05:55

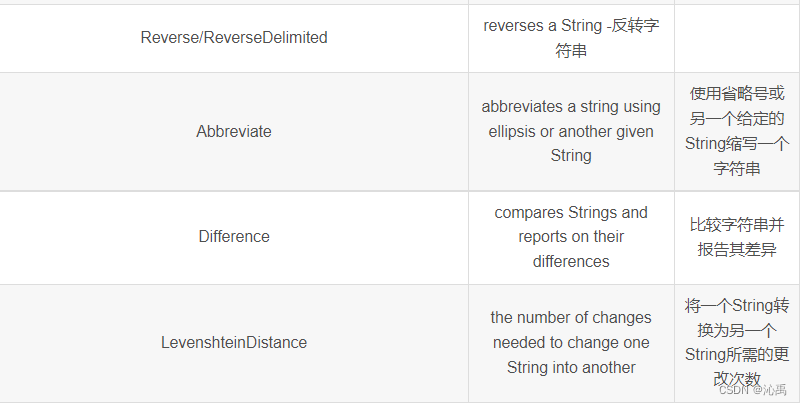
isEmpty 和 isBlank 的用法区别，居然一半的人答不上来.....

isEmpty 和 isBlank 的用法区别 isEmpty系列isBank系列 hi&#xff01;我是沁禹&#xff5e; 也许你两个都不知道,也许你除了isEmpty/isNotEmpty/isNotBlank/isBlank外,并不知道还有isAnyEmpty/isNoneEmpty/isAnyBlank/isNoneBlank的存在, come on ,让我们一起来探索org.apache…...

编程日记 2024/1/5 20:04:54

数据分析求职-简历准备

简历在整个求职过程中的重要性不言而喻&#xff0c;今天咱们来聊求职过程中简历准备的那些事儿~ 1. 简历究竟有啥用 求职的流程简单说就是&#xff1a;网申->笔试->面试->offer 其中网申环节&#xff0c;简历100%决定了你的通过与否&#xff0c;这个点大家都知道。…...

编程日记 2024/1/5 20:03:53

亚马逊店铺遇到账号申诉模版分享

1.表达诚意&#xff0c;先认错再说&#xff1a;我知道&#xff0c;最近我们在Amazon.com上作为卖家的表现已经低于亚马逊和我们自己的质量标准。 2.清楚分明的格式&#xff1a;我们库存管理的混乱导致了延迟发货&#xff0c;更糟糕的是&#xff0c;物品无法使用。当延迟发货和…...

编程日记 2024/1/5 20:02:52

2023年广东省网络安全A模块（笔记详解）

模块A 基础设施设置与安全加固 一、项目和任务描述&#xff1a; 假定你是某企业的网络安全工程师&#xff0c;对于企业的服务器系统&#xff0c;根据任务要求确保各服务正常运行&#xff0c;并通过综合运用登录和密码策略、流量完整性保护策略、事件监控策略、防火墙策略等多…...

编程日记 2024/1/5 20:00:51

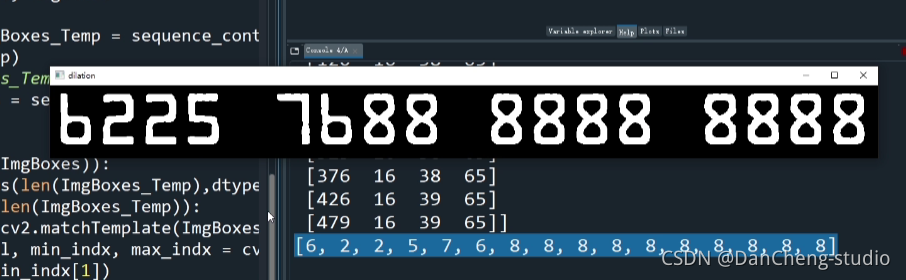
竞赛保研 基于机器视觉的银行卡识别系统 - opencv python

1 前言 &#x1f525; 优质竞赛项目系列&#xff0c;今天要分享的是 基于深度学习的银行卡识别算法设计 该项目较为新颖&#xff0c;适合作为竞赛课题方向&#xff0c;学长非常推荐&#xff01; &#x1f9ff; 更多资料, 项目分享&#xff1a; https://gitee.com/dancheng…...

编程日记 2024/1/5 19:58:49

书摘：C 嵌入式系统设计模式 04

本书的原著为&#xff1a;《Design Patterns for Embedded Systems in C ——An Embedded Software Engineering Toolkit 》&#xff0c;讲解的是嵌入式系统设计模式&#xff0c;是一本不可多得的好书。 本系列描述我对书中内容的理解。 实现类的最简单方法是使用文件作为封装…...

编程日记 2024/1/5 19:57:48

C 练习实例16 - 最大公约数和最小公倍数

题目&#xff1a;输入两个正整数a和b&#xff0c;求其最大公约数和最小公倍数 数学&#xff1a;最大公约数*最小公倍数a*b 例如&#xff1a;a16&#xff0c;b20。最小公倍数80&#xff0c;最大公约数4。80*416*20。 算法&#xff1a;辗转相除法&#xff0c;又称欧几里德算法…...

编程日记 2024/1/5 19:56:47

GAN-概念和应用场景

概念和应用 生成对抗网络 &#xff08;GAN&#xff09; 的 18 个令人印象深刻的应用 by 杰森布朗利 on July 12&#xff0c; 2019 in 生成对抗网络110 鸣叫 共享 生成对抗网络 &#xff08;GAN&#xff09; 是一种用于生成建模的神经网络架构。 生成式建模涉及使用模型生成可…...

编程日记 2024/1/5 19:54:45

LeetCode(36)有效的数独 ⭐⭐

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 &#xff0c;验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。&#xff08;请参考示例图&#xff09; 注…...

编程日记 2024/1/5 19:53:44

用LCD显示字符‘A‘

#include<reg51.h> //包含单片机寄存器的头文件 #include<intrins.h> //包含_nop_()函数定义的头文件 sbit RSP2^0; //寄存器选择位&#xff0c;将RS位定义为P2.0引脚 sbit RWP2^1; //读写选择位&#xff0c;将RW位定义为P2.1引脚 sbit EP2^2; //使能…...

编程日记 2024/1/5 19:51:43

Zookeeper相关问题及答案(2024)

1、ZooKeeper是什么&#xff1f;它的主要用途是什么&#xff1f; ZooKeeper 是一个由 Apache 预先开发和维护的开源服务器&#xff0c;用于协调分布式应用程序。它是一个集中式服务&#xff0c;为分布式应用提供一致性保障&#xff0c;配置管理&#xff0c;命名&#xff0c;同…...

编程日记 2024/1/5 19:46:39

1.大数据概述

目录 概述hadoophadoop 模块hadoop 发行版apache社区版本CDP(CDHHDP)其它云产商框架选择 hadoop 安装 结束 概述 先了解几个常用的网站 apache 官网hadoop 官网hadoop githubhttps://github.com/apache/xxx [https://github.com/apache/spark (example)] hadoop hadoop 模块…...

编程日记 2024/1/5 19:44:37

NGUI基础-Widget

目录 Widget是什么 Widget组件包含的属性 Pivot Depth Size snap Aspect Free Based on Width Based on Height Widget是什么 在Unity UI系统中&#xff0c;"Widget"是指UI元素的基类&#xff0c;它为UI元素提供了位置、大小和锚点等基本属性。通过使用&qu…...

编程日记 2024/1/5 19:43:36

SpringBoot集成沙箱支付

前言 支付宝沙箱支付&#xff08;Alipay Sandbox Payment&#xff09;是支付宝提供的一个模拟支付环境&#xff0c;用于开发和测试支付宝支付功能的开发者工具。在真实的支付宝环境中进行支付开发和测试可能涉及真实资金和真实用户账户&#xff0c;而沙箱环境则提供了一个安全…...

编程日记 2024/1/5 19:42:35

BUUCTF--gyctf_2020_borrowstack1

这是一题栈迁移的题目&#xff0c;先看看保护&#xff1a; 黑盒测试&#xff1a; 用户可输入两次内容&#xff0c;接着看看IDA中具体程序流程&#xff1a; 我们看到溢出内容只有0x10的空间给我们布局&#xff0c;这显然是不足以我们布置rop的。因此肯定就是栈迁移了。迁到什么地…...

编程日记 2024/1/5 19:40:33

图像分割-Grabcut法(C#)

版权声明&#xff1a;本文为博主原创文章&#xff0c;转载请在显著位置标明本文出处以及作者网名&#xff0c;未经作者允许不得用于商业目的。 本文的VB版本请访问&#xff1a;图像分割-Grabcut法-CSDN博客 GrabCut是一种基于图像分割的技术&#xff0c;它可以用于将图像中的…...

编程日记 2024/1/5 19:36:30

C# WPF上位机开发（Web API联调）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 很多时候&#xff0c;客户需要开发的不仅仅是一个上位机系统&#xff0c;它还有其他很多配套的系统或设备&#xff0c;比如物流小车、立库、数字孪…...

编程日记 2024/1/5 19:35:30

c语言：用结构体求平均分｜练习题

一、题目 用c语言的结构体&#xff0c;求4位学生成绩的平均分 如图&#xff1a; 二、代码截图【带注释】 三、源代码【带注释】 #include <stdio.h> float aver();//声明平均分函数 void printScore();//声明打印函数 //设置结构体&#xff0c; struct student { …...

编程日记 2024/1/5 19:32:27

echarts 仪表盘进度条 相关配置

option {series: [{type: gauge,min: 0,//最大值max: 100, //最小值startAngle: 200,//仪表盘起始角度。圆心 正右手侧为0度&#xff0c;正上方为90度&#xff0c;正左手侧为180度。endAngle: -20,//仪表盘结束角度splitNumber: 100, //仪表盘刻度的分割段数itemStyle: {color…...

编程日记 2024/1/5 19:31:25

Simpy：Python之离散时间序列仿真

Simpy&#xff1a;Python之离散时间序列仿真 文章目录 Simpy&#xff1a;Python之离散时间序列仿真简介基本使用语法简单案例在数据中心中的应用案例 简介 下载地址网站&#xff1a; https://pypi.org/project/simpy/ 有关教程网站&#xff1a; https://simpy.readthedocs.…...

编程日记 2024/1/5 19:30:24

连接GaussDB(DWS)报错：Invalid or unsupported by client SCRAM mechanisms

用postgres方式连接GaussDB(DWS)报错&#xff1a;Invalid or unsupported by client SCRAM mechanisms 报错内容 [2023-12-27 21:43:35] Invalid or unsupported by client SCRAM mechanisms org.postgresql.util.PSQLException: Invalid or unsupported by client SCRAM mec…...

编程日记 2024/1/5 19:29:24

汽车标定技术(十四)--标定数据固化方法简介

目录 1.标定数据固化方法 1.1 基于XCP固化 1.2 基于UDS固化 2. 具体实现形式 2.1 CAN...

编程日记 2024/1/5 19:28:23

2024年关键技术发展战略趋势前瞻

技术趋势在不断变化&#xff0c;但总的趋势是技术日益深入人类生活的方方面面&#xff0c;这些趋势可能会对未来的科技发展和人类生活产生深远影响&#xff0c;以下是预计今年将塑造未来的一些关键技术趋势。 更多的人将采用人工智能和机器学习 人工智能(AI)和机器学习(ML)不…...

编程日记 2024/1/5 19:27:21

Java程序设计——GUI设计

一、目的 通过用户图形界面设计&#xff0c;掌握JavaSwing开发的基本方法。 二、实验内容与设计思想 实验内容&#xff1a; 课本验证实验&#xff1a; Example10_6 图 1 Example10_7 图 2 图 3 Example10_15 图 4 设计思想&#xff1a; ①学生信息管理系统&#xff1a…...

编程日记 2024/1/5 19:22:16

three.js Raycaster(鼠标点击选中模型)

效果&#xff1a; 代码&#xff1a; <template><div><el-container><el-main><div class"box-card-left"><div id"threejs" style"border: 1px solid red"></div><div class"box-right"…...

编程日记 2024/1/5 19:20:14

网站建设销售怎么样/淘宝推广费用一般多少

作为一个程序员来说&#xff0c;简历可谓是面试的时候一个加分砝码&#xff0c;往往有的面试者只在意自己的技术&#xff0c;其实这是非常不对的。简历对于一个面试者来说非常重要&#xff0c;他是第一个入口&#xff0c;也是面试官认识你的第一个途径。不管是对于刚毕业或者即…...

编程日记 2024/10/30 20:39:22

购物网站app开发多少钱/seo建站优化推广

一.在屏幕上显示"Hello World!" /*显示“Hello World&#xff01;”。*/ #include<stdio.h> int main(void) {printf("Hello World!"); return 0; }/*注释文本*/ :是程序的注释&#xff0c;用来说明程序的功能&#xff0c;注释文本必须包含在/*和*/…...

编程日记 2024/10/30 19:16:24

广州旅游网站建设设计公司/西安seo排名优化推广价格

一、机制 对象关系映射&#xff08;Object Relational Mapping&#xff0c;ORM&#xff09;&#xff0c;将对数据库的操作&#xff0c;映射为对类的操作&#xff0c;一个表对应一个类。sqlalchemy无法独立对数据库进行操作&#xff0c;需要借助其他第三方插件&#xff0c…...

编程日记 2024/10/30 17:32:35

福建省建设职业管理中心网站/最新长尾关键词挖掘

本文实例为大家分享了java递归输出树形菜单的具体代码&#xff0c;供大家参考&#xff0c;具体内容如下首先我们要建立树节点的类&#xff1a;package com.tree;public class Node {private Integer id;private Integer parentId;private String name;private String link;publ…...

编程日记 2024/10/30 16:37:05

商务网站规划设计要点/品牌策划方案模板

转载自http://cnlearn.linksprite.com/?p5248#.VwZrzvl95hE 数字 I/O &#xff08;1&#xff09;pinMode(pin, mode) 数字IO 口输入输出模式定义函数&#xff0c;pin 表示为0&#xff5e;13&#xff0c; mode 表示为INPUT 或OUTPUT 。&#xff08;2&#xff09; digitalWrite(…...

编程日记 2024/10/30 16:25:00

国外平面设计/优化网站做什么的

BCD码一般在时钟芯片中会采用&#xff0c;比如2019-03-29 15:42:54会表示为 0x20 0x19 0x03 0x29 0x15 0x42 0x54&#xff0c;具体十进制跟BCD码的关系可以百度&#xff1b;BCD转为十进制 int BCDToInt(unsigned char value) {int temp 0;temp (value>>4)*10;temp va…...

编程日记 2024/10/30 15:02:08