箭头函数 - JavaScript的新宠儿
📢 鸿蒙专栏:想学鸿蒙的,冲
📢 C语言专栏:想学C语言的,冲
📢 VUE专栏:想学VUE的,冲这里
📢 CSS专栏:想学CSS的,冲这里
📢 Krpano专栏:想学VUE的,冲这里
📢 JavaScript专栏:想学JavaScript的,冲这里
🔔 上述专栏,都在不定期持续更新中!!!!!!!

目录
✨ 前言
箭头函数的基本语法:
this绑定
调用限制
其他特点
✨ 结语
✨ 前言
自ECMAScript 6起,JavaScript中引入了箭头函数,这是ES6最让人兴奋的特性之一。它极大地简化了函数的定义方式,让代码更加简洁。你是否也想立即掌握这个强大的新功能,但又不知道该如何使用?本文将全面解析箭头函数的用法、优缺点和场景运用,带你完全领会箭头函数的强大魅力。准备好你的JavaScript大脑,我们开始吧!

箭头函数的基本语法:
const func = (arg1, arg2) => expression;这样简洁的语法适用于只有一个表达式的函数:
const add = (a, b) => a + b;如果函数体有多条语句,需要用花括号 {} 括起来:
const sum = (a, b) => {let result = a + b;return result;
}这里有几个关键点:
- 使用
=>定义函数,左侧为参数,右侧为函数体 - 当只有一个参数,可以省略括号
- 函数体如果只有一个表达式,可以省略大括号{},表达式结果会默认返回
举个例子:
// 两个参数
const add = (a, b) => a + b; // 无参数
const showMsg = () => console.log('Hello');// 多行函数体需要加{}
const sum = (a, b) => {let result = a + b;return result;
}这就定义了三个箭头函数。语法简洁许多。
this绑定
箭头函数不绑定this,this的值继承自外围作用域。例如:
const obj = {name: 'Jack',print: () => {console.log(this.name); // this为全局对象 }
}print()里的this不是绑定到obj对象,而是继承自全局作用域。
调用限制
箭头函数不能用作构造函数,不能使用new命令,也就不能绑定prototype。
同样也不能用call、apply、bind来改变this的绑定对象。
其他特点
箭头函数不能作为Generator函数,不能使用yield关键字。
也不支持arguments变量。
箭头函数还有一些特别的地方需要注意:
- 函数体只有一条语句,
return可以省略- 没有自己的
this,this的值继承自外围作用域- 无法通过
new关键字调用,所以也就没有了prototype- 不可以改变
this的绑定,所以不适用于定义对象方法- 不能作为 Generator 函数,不能使用
yield关键字
尽管有一些限制,但箭头函数作为一种更简洁的函数表达式语法,适用于许多常见的函数场景,可以让我们的代码更加简洁。它很好地满足了函数式编程的需求。
所以,在适当的场景下使用箭头函数,可以让我们的代码更加简介易读。它是JavaScript中一个非常棒的新特性,快去尝试使用箭头函数吧!
✨ 结语
通过今天的学习,我们已经全面了解了JavaScript ES6中的箭头函数,包括语法定义、this绑定、省略return、调用限制等特性。合理使用箭头函数可以让我们的代码更加简洁优雅。但也要注意它的限制,不可滥用。总之,箭头函数是一个非常nice的ES6新特性,它将极大地推动函数式编程在JavaScript中的发展。如果你喜欢这篇博客,欢迎分享给你的编程伙伴一起get新知!
我们改日再会

相关文章:

箭头函数 - JavaScript的新宠儿
📢 鸿蒙专栏:想学鸿蒙的,冲 📢 C语言专栏:想学C语言的,冲 📢 VUE专栏:想学VUE的,冲这里 📢 CSS专栏:想学CSS的,冲这里 Ǵ…...
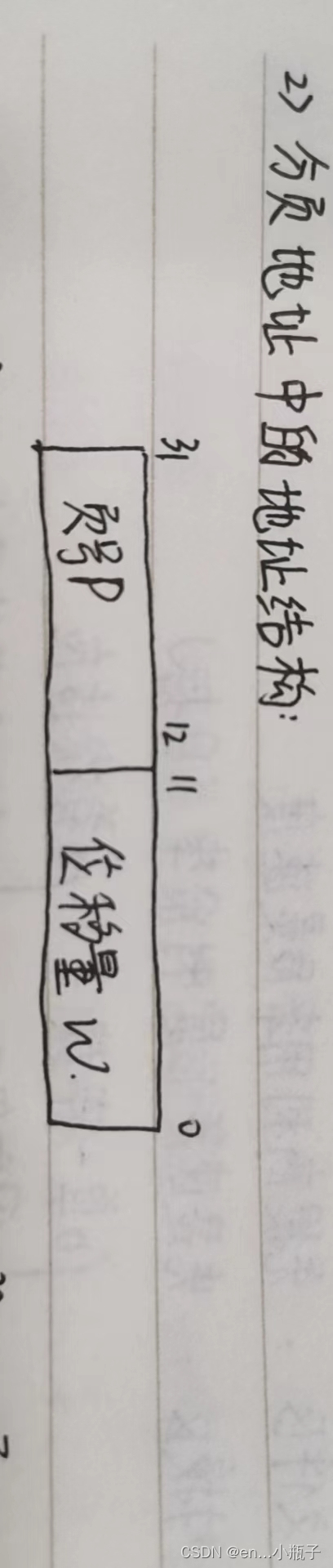
操作系统期末复习知识点
目录 一.概论 1.操作系统的介绍 2.特性 3.主要功能 4.作用 二.进程的描述与控制 1.进程的定义 2.特性 3.进程的创建步骤 4.基本状态转化 5.PCB的作用 6.进程与线程的比较 三.进程同步 1.同步的概念(挺重要的) 2.临界区 3.管程和进程的区…...

[英语学习][23][Word Power Made Easy]的精读与翻译优化
[序言] 译者的这次翻译, 完全直译, 生硬无比. [英文学习的目标] 提升自身的英语水平, 对日后编程技能的提升有很大帮助. 希望大家这次能学到东西, 同时加入我的社区讨论与交流英语相关的内容. [原著英文与翻译版对照][第22页] Knowledge is chiefly in the form of words…...

吉林大学19、21级计算机学院《计算机网络》期末真题试题
一、21级(考后回忆) 一、不定项选择(一共10个选择题,一个两分,选全得满分) 不定项:可以选择1~4个 考点有: ①协议、服务 ②码分多路复用通过接受码片序列,求哪个站点发送…...

python练习3【题解///考点列出///错题改正】
一、单选题 1.【单选题】 ——可迭代对象 下列哪个选项是可迭代对象( D)? A.(1,2,3,4,5) B.[2,3,4,5,6] C.{a:3,b:5} D.以上全部 知识点补充——【可迭代对象】 可迭代对象(iterable)是指可以通过迭代ÿ…...

LINUX服务器防火墙nf_conntrack问题一例
一、故障现象 业务反馈服务异常,无法响应请求,从系统日志 dmesg 或 /var/log/messages 看到大量以下记录:kernel: nf_conntrack: table full, dropping packet. 二、问题分析 业务高峰期服务器访问量大,内核 netfilter 模块 conntrack 相关参…...
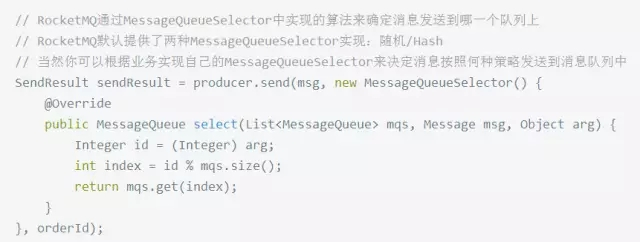
经典八股文之RocketMQ
核心概念 NameServer nameserver是整个rocketmq的大脑,是rocketmq的注册中心。broker在启动时向所有nameserver注册。生产者在发送消息之前先从 NameServer 获取 Broker 服务器地址列表(消费者一 样),然后根据负载均衡算法从列表中选择一台服务器进行消…...

Pandas之从sql库中导入数据的几种方法分析
1.使用mysql-connector-python库将SQL文件导入到Python中,并查询数据库中的表 确保已经安装mysql-connector-python库 #导入模块 import mysql.connector# 建立与MySQL数据库的连接 conn mysql.connector.connect(host"localhost",user"username&…...

18. Mysql 存储过程,实现动态数据透视
文章目录 概述常见操作创建存储过程存储过程局部变量定义和赋值查看存储过程删除存储过程调用存储过程 示例-动态数据透视详细讲解总结参考资料 概述 Mysql 存储过程是一组预先编译的 sql 语句集合,它们被存储在数据库中,并可以被多次调用执行。存储过程…...

VuePress部署到GitHub Pages
一、git push自动部署 1、创建用于工作流的文件 在项目根目录下创建一个用于 GitHub Actions 的工作流 .yml 文件 name: docson:# 每当 push 到 main 分支时触发部署push:branches: [main]# 手动触发部署workflow_dispatch:jobs:docs:runs-on: ubuntu-lateststeps:- uses: a…...
git 本地仓库
本地仓库 start.bat 启动...
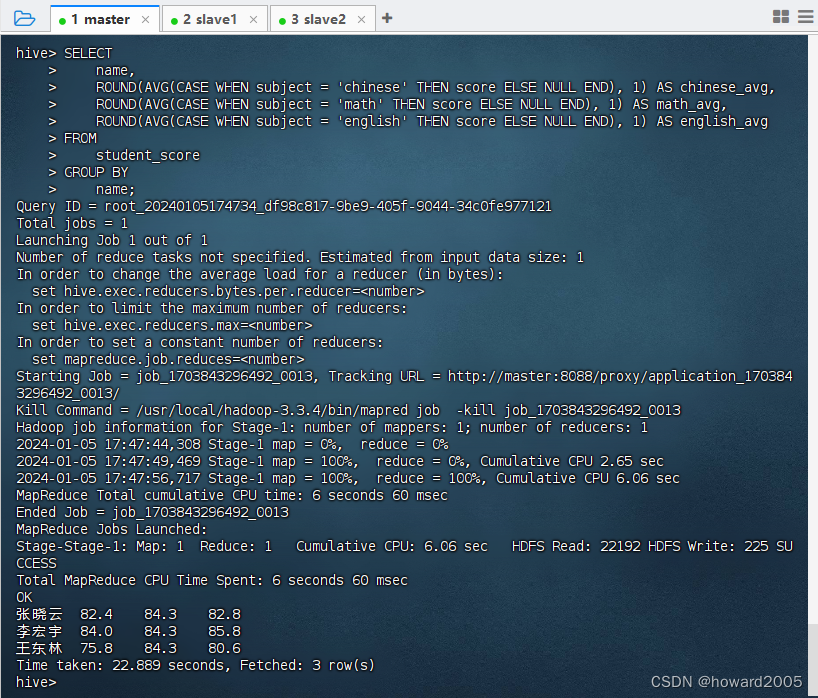
Hive实战:分科汇总求月考平均分
文章目录 一、实战概述二、提出任务三、完成任务(一)准备数据1、在虚拟机上创建文本文件2、上传文件到HDFS指定目录 (二)实现步骤1、启动Hive Metastore服务2、启动Hive客户端3、创建分区的学生成绩表4、按分区加载数据5、查看分区…...

快速搭建知识付费小程序,3分钟即可开启知识变现之旅
明理信息科技知识付费saas租户平台 在当今数字化时代,知识付费已经成为一种趋势,越来越多的人愿意为有价值的知识付费。然而,公共知识付费平台虽然内容丰富,但难以满足个人或企业个性化的需求和品牌打造。同时,开发和…...

【计算机图形学划重点】第一讲-Pipeline and Introduction
基础知识 Vertex(顶点) define the location of primitives in space, and consists of vertex stream. 顶点用于定义空间中基本图形(primitives)的位置。它包含了一个顶点流(vertex stream),…...
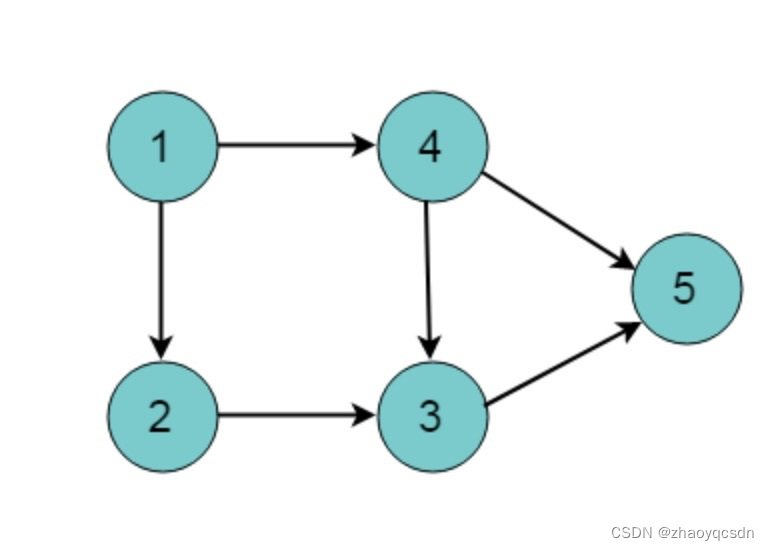
面试题-DAG 有向无环图
有向无环图用于解决前后依赖问题,在Apollo中用于各个组件的依赖管理。 在算法面试中,有很多相关题目 比如排课问题,有先修课比如启动问题,需要先启动1,才能启动2 概念 顶点: 图中的一个点,比…...
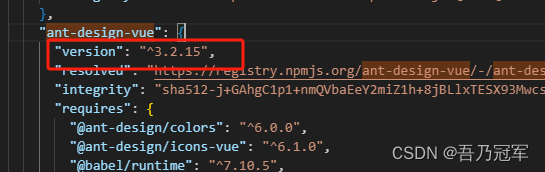
vite + vue3引入ant design vue 报错
npm install ant-design-vue --save下载插件并在main.ts 全局引入 报错 解决办法一: main.ts注释掉全局引入 模块按需引入 解决办法二 将package.json中的ant-design-vue的版本^4.0.0-rc.4改为 ^3.2.15版本 同时将将package-lock.json中的ant-design-vue的版本…...

使用EasyPoi导入数据并返回失败xls
添加依赖 <!-- https://mvnrepository.com/artifact/cn.afterturn/easypoi-base --> <dependency><groupId>cn.afterturn</groupId><artifactId>easypoi-base</artifactId><version>4.4.0</version> </dependency> 工…...
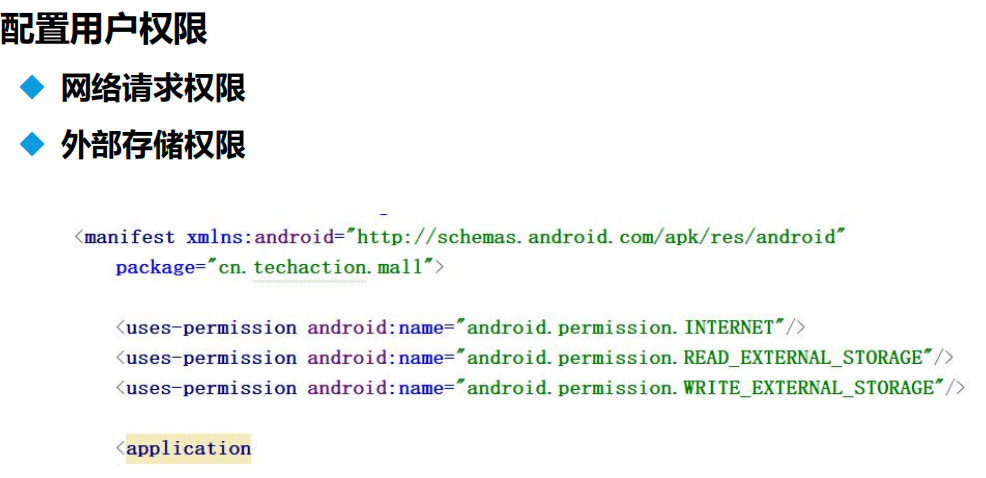
机械配件移动商城课程概述
项目介绍 开发准备 任务 开源库介绍 框架搭建 工具类...

prometheus-docker 快速安装
镜像加速 sudo mkdir -p /etc/docker sudo tee /ect/docker/daemon.json << "EOF" {"register-mirros": ["http://hub-mirror.c.163.com"] } EOF安装docker export DOWNLOAD_URL"http://mirrors.163.com/docker-ce" curl -fsSl…...

RabbitMQ 核心概念(交换机、队列、路由键),队列类型等介绍
RabbitMQ 核心概念(交换机、队列、路由键),队列类型等介绍 RabbitMQ 是一个消息队列系统,它的核心概念包括交换机(Exchange)、队列(Queue)和路由键(Routing Key),它们一起…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 )
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
