最优化理论分析复习--最优性条件(一)
文章目录
- 上一篇
- 无约束问题的极值条件
- 约束极值问题的最优性条件
- 基本概念
- 只有不等式约束时
- 下一篇
上一篇
最优化理论复习–对偶单纯形方法及灵敏度分析
无约束问题的极值条件
由于是拓展到向量空间 R n R^n Rn, 所以可由高数中的极值条件进行类比
-
一阶必要条件
设函数 f ( x ) f(x) f(x) 在点 x ˉ \bar{x} xˉ 处可微, 若 x ˉ \bar{x} xˉ 是局部极小点,则 ▽ f ( x ˉ ) = 0 \bigtriangledown f(\bar{x}) = 0 ▽f(xˉ)=0
类比于若 x ˉ \bar{x} xˉ 是极小值点则 f ′ ( x ˉ ) = 0 f'(\bar{x}) = 0 f′(xˉ)=0 -
二阶必要条件
设 f ( x ) f(x) f(x) 在 x ˉ \bar{x} xˉ 处二阶可微,若 x ˉ \bar{x} xˉ 是局部极小点, 则 ▽ f ( x ˉ ) = 0 \bigtriangledown f(\bar{x}) = 0 ▽f(xˉ)=0, 且 H e s s i a n Hessian Hessian 矩阵 ▽ 2 f ( x ˉ ) \bigtriangledown^2f(\bar{x}) ▽2f(xˉ) 是半正定的。
类比于 若 x ˉ \bar{x} xˉ是极小值点则 f ′ ( x ˉ ) = 0 , 且 f ′ ′ ( x ˉ ) ≥ 0 f'(\bar{x}) = 0, 且 f''(\bar{x}) \geq 0 f′(xˉ)=0,且f′′(xˉ)≥0 -
二阶充分条件
设函数 f ( x ) f(x) f(x) 在点 x ˉ \bar{x} xˉ 处二次可微,若梯度 ▽ f ( x ˉ ) = 0 \bigtriangledown f(\bar{x}) = 0 ▽f(xˉ)=0, 且 H e s s i a n Hessian Hessian 矩阵 ▽ 2 f ( x ˉ ) 正 定 \bigtriangledown^2f(\bar{x})正定 ▽2f(xˉ)正定, 则 x ˉ \bar{x} xˉ是严格局部极小点。
类比于 f ′ ( x ˉ ) = 0 , f ′ ′ ( x ˉ ) > 0 f'(\bar{x}) = 0, f''(\bar{x}) > 0 f′(xˉ)=0,f′′(xˉ)>0则 x ˉ \bar{x} xˉ 是极小值点 -
充要条件
设 f ( x ) f(x) f(x) 是定义在 R n R^n Rn 上的可微凸函数, x ˉ ∈ R n \bar{x} \in R^n xˉ∈Rn, 则 x ˉ \bar{x} xˉ 为整体极小点的充要条件是 ▽ f ( x ˉ ) = 0 \bigtriangledown f(\bar{x}) = 0 ▽f(xˉ)=0
注:如果 f ( x ) f(x) f(x) 是严格凸的,则全局极小点是唯一的。



约束极值问题的最优性条件
基本概念
定义: 对 m i n f ( x ) min f(x) minf(x), 设 x ˉ ∈ R n \bar{x} \in R^n xˉ∈Rn 是任给一点, d ≠ 0 d \not = 0 d=0, 若存在 δ > 0 \delta > 0 δ>0, 使得对任意的 λ ∈ ( 0 , δ ) \lambda \in (0, \delta) λ∈(0,δ), 有 f ( x ˉ + λ d ) < f ( x ˉ ) f (\bar{x} + \lambda d) < f(\bar{x}) f(xˉ+λd)<f(xˉ), 则称 d d d 为 f ( x ) f(x) f(x) 在点 x ˉ \bar{x} xˉ 处的下降方向。
-
引理: 设函数 f ( x ) f(x) f(x) 在点 x ˉ \bar{x} xˉ 可微, 若存在 d ≠ 0 d \not = 0 d=0, 使得 ▽ f ( x ˉ ) T d < 0 \bigtriangledown f(\bar{x})^T d < 0 ▽f(xˉ)Td<0, 则存在 δ > 0 \delta > 0 δ>0, 是使得对 ∀ λ ∈ ( 0 , δ ) \forall \lambda \in (0, \delta) ∀λ∈(0,δ), 有 f ( x ˉ + λ d ) < f ( x ˉ ) f(\bar{x} + \lambda d)<f(\bar{x}) f(xˉ+λd)<f(xˉ)。
即与梯度方向成钝角的方向是下降方向
表示为
F 0 = { d ∣ ▽ f ( x ˉ ) T d < 0 } F_0 = \{ d | \bigtriangledown f(\bar{x})^T d < 0\} F0={d∣▽f(xˉ)Td<0} -
定义: 设集合 S ⊂ R n , x ˉ ∈ c l S . S \subset R^n, \bar{x} \in clS. S⊂Rn,xˉ∈clS., d d d 为非零向量, 若存在数 δ > 0 \delta > 0 δ>0, 使得对任意 λ ∈ ( 0 , δ ) , \lambda \in (0, \delta), λ∈(0,δ), 都有 x ˉ + λ d ∈ S \bar{x} + \lambda d \in S xˉ+λd∈S 则称 d d d 为集合 S S S 在 x ˉ \bar{x} xˉ 的可行方向。
就是移动方向在可行域内
表示为 D = { d ∣ d ≠ 0 , x ˉ ∈ c l S , ∃ δ > 0 , ∀ λ ∈ ( 0 , δ ) , 有 x ˉ + λ d ∈ S } D = \{ d | d \not = 0, \bar{x} \in clS, \exists \delta > 0, \forall \lambda \in (0, \delta), 有 \bar{x} + \lambda d \in S \} D={d∣d=0,xˉ∈clS,∃δ>0,∀λ∈(0,δ),有xˉ+λd∈S}
x ˉ 处 的 可 行 方 向 锥 \bar{x} 处的可行方向锥 xˉ处的可行方向锥 -
定义: 若问题的可行点 x ˉ \bar{x} xˉ 是某个不等式约束 g i ( x ) ≥ 0 g_i(x) \geq 0 gi(x)≥0 变成等式, 则该不等式约束称为关于可行点 x ˉ \bar{x} xˉ 的起作用约束; 否则称为不起作用约束。
表示为
I = { i ∣ g i ( x ˉ = 0 , x ˉ ∈ S ) } I = \{ i| g_i(\bar{x} = 0, \bar{x} \in S) \} I={i∣gi(xˉ=0,xˉ∈S)} -
定义:在起作用约束作对应切线,获得对应梯度,与这两个梯度同时呈锐角的方向为积极约束的可行方向。
表示为 G 0 = { d ∣ ▽ g i ( x ˉ ) T d > 0 , i ∈ I ( x ) } G_0 = \{d | \bigtriangledown g_i(\bar{x})^T d > 0, i \in I(x) \} G0={d∣▽gi(xˉ)Td>0,i∈I(x)}
即由约束条件求出的可行方向
有 G 0 ⊂ D G_0 \subset D G0⊂D
问题标准形式:
m i n f ( x ) \ \ \ \ \ \ \ \ min f(x) minf(x)
s . t . { g i ( x ) ≥ 0 , 不 等 式 约 束 h j ( x ) = 0 , 等 式 约 束 x ∈ R n s.t.\left \{\begin{matrix} g_i (x) \geq 0,不等式约束 \\ \\h_j(x) = 0,等式约束 \\ \\ x \in R^n \end {matrix} \right. s.t.⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧gi(x)≥0,不等式约束hj(x)=0,等式约束x∈Rn
几何最优性条件:设 S S S 是 R n R^n Rn 的非空集合, x ˉ ∈ S , f ( x ) \bar{x} \in S, f(x) xˉ∈S,f(x)在 x ˉ \bar{x} xˉ 处可微, 若 x ˉ \bar{x} xˉ 是局部最优解, 则 F 0 ∩ D = ∅ F_0 \cap D = \emptyset F0∩D=∅
即所有的可行方向都是上升方向
只有不等式约束时
由于 G 0 ⊂ D G_0 \subset D G0⊂D 所以也有 F 0 ∩ G 0 = ∅ F_0 \cap G_0 = \emptyset F0∩G0=∅,可行域之内不能有空洞
- (F-J条件) 设 x ˉ ∈ S , I = { i ∣ g i ( x ˉ ) = 0 } , f ( x ) , g i ( x ) ( i ∈ I ) \bar{x} \in S, I = \{ i | g_i(\bar{x}) = 0\}, f(x), g_i(x) (i \in I) xˉ∈S,I={i∣gi(xˉ)=0},f(x),gi(x)(i∈I) 在 x ˉ \bar{x} xˉ 处可微, g i ( x ) ( i ∉ I ) g_i(x) (i \notin I) gi(x)(i∈/I) 在 x ˉ \bar{x} xˉ 处连续, 若 x ˉ \bar{x} xˉ 是问题的最优解,则存在不全为零的数 w 0 , w i ( i ∈ I ) w_0, w_i (i \in I) w0,wi(i∈I) 使得
w 0 ▽ f ( x ˉ ) − ∑ i ∈ I w i ▽ g i ( x ˉ ) = 0 w_0 \bigtriangledown f(\bar{x}) - \sum\limits_{i \in I} w_i \bigtriangledown g_i(\bar{x}) = 0 w0▽f(xˉ)−i∈I∑wi▽gi(xˉ)=0
称 x ˉ \bar{x} xˉ 为 F − J F-J F−J 点
为必要条件,极小值点一定是 F-J点, 但 F-J点不一定为极小值点


当 w 0 = 0 w_0 = 0 w0=0 是另外另个约束条件的梯度必须能相互抵消,这种情况才有最优解,因此更多的是关注 w 0 ≠ 0 w_0 \not = 0 w0=0的情况
- (KKT条件) 设 x ˉ ∈ S \bar{x} \in S xˉ∈S , f , g i ( i ∈ I ) 在 x ˉ 处 可 微 , g i ( i ∉ I ) 在 x ˉ 连 续 f, g_i(i \in I)在\bar{x} 处可微, g_i(i \notin I) 在\bar{x}连续 f,gi(i∈I)在xˉ处可微,gi(i∈/I)在xˉ连续(保证无空洞), { ▽ g i ( x ˉ ) ∣ i ∈ I } 线 性 无 关 \{ \bigtriangledown g_i(\bar{x}) | i \in I\} 线性无关 {▽gi(xˉ)∣i∈I}线性无关, 若 x ˉ \bar{x} xˉ 是局部最优解, 则存在非负数 w i , i ∈ I , w_i, i \in I, wi,i∈I, 使得
▽ f ( x ˉ ) − ∑ i ∈ I w i ▽ g i ( x ˉ ) = 0 \bigtriangledown f(\bar{x}) - \sum\limits_{i \in I} w_i \bigtriangledown g_i(\bar{x}) = 0 ▽f(xˉ)−i∈I∑wi▽gi(xˉ)=0

凸规划的判别方法:
- 可行域是凸集, 目标函数是凸函数
- 可行域是 ≥ \geq ≥的凹函数, 目标函数是凸函数
求KKT点
- KKT条件的另一种表述
设 x ˉ ∈ S \bar{x} \in S xˉ∈S , f , g i ( i ∈ I ) 在 x ˉ f, g_i(i \in I)在\bar{x} f,gi(i∈I)在xˉ 处可微, { ▽ g i ( x ˉ ) ∣ i ∈ I } 线 性 无 关 \{ \bigtriangledown g_i(\bar{x}) | i \in I\}线性无关 {▽gi(xˉ)∣i∈I}线性无关, 若 x ˉ \bar{x} xˉ 是局部最优解, 则存在非负数 w i , i = 1 , 2... m w_i, i =1,2...m wi,i=1,2...m 使得
{ ▽ f ( x ˉ ) − ∑ i = 1 m w i ▽ g i ( x ˉ ) = 0 ( 没 要 求 对 应 的 g i ( x ) 为 约 束 条 件 ) w i g i ( x ˉ ) = 0 , i = 1 , 2... m ( 互 补 松 弛 条 件 ) w i ≥ 0 i = 1 , 2... m \left \{\begin{matrix} \bigtriangledown f(\bar{x}) - \sum\limits_{i = 1}^{m} w_i \bigtriangledown g_i(\bar{x}) = 0(没要求对应的g_i(x)为约束条件) \\ \\w_ig_i(\bar{x}) = 0, i = 1, 2...m (互补松弛条件) \\ \\ w_i \geq 0 i = 1,2...m \end {matrix} \right. ⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧▽f(xˉ)−i=1∑mwi▽gi(xˉ)=0(没要求对应的gi(x)为约束条件)wigi(xˉ)=0,i=1,2...m(互补松弛条件)wi≥0i=1,2...m
通过这个表述方式,加上原来的约束然后将所有的方程列出来求解


有人会算的话请留言,感谢
下一篇
最优化理论复习–最优性条件(二)
相关文章:

最优化理论分析复习--最优性条件(一)
文章目录 上一篇无约束问题的极值条件约束极值问题的最优性条件基本概念只有不等式约束时 下一篇 上一篇 最优化理论复习–对偶单纯形方法及灵敏度分析 无约束问题的极值条件 由于是拓展到向量空间 R n R^n Rn, 所以可由高数中的极值条件进行类比 一阶必要条件 设函数 f (…...

基于WIFI指纹的室内定位算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 4.1WIFI指纹定位原理 4.2 指纹数据库建立 4.3定位 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 .....................................…...
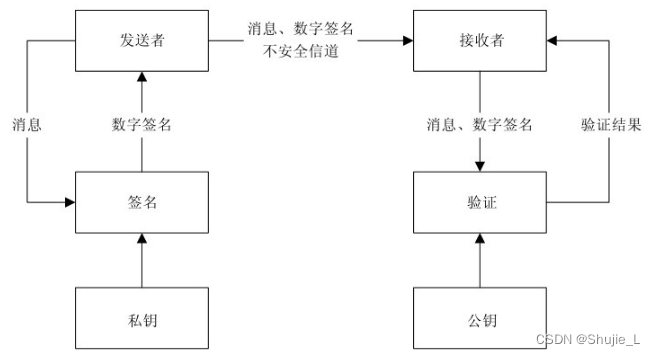
密码学:一文读懂非对称密码体制
文章目录 前言非对称密码体制的保密通信模型私钥加密-公钥解密的保密通信模型公钥加密-私钥解密的保密通信模型 复合式的非对称密码系统散列函数数字签名数字签名满足的三个基本要求先加密还是先签名?数字签名成为公钥基础设施以及许多网络安全机制的基础什么是单向…...
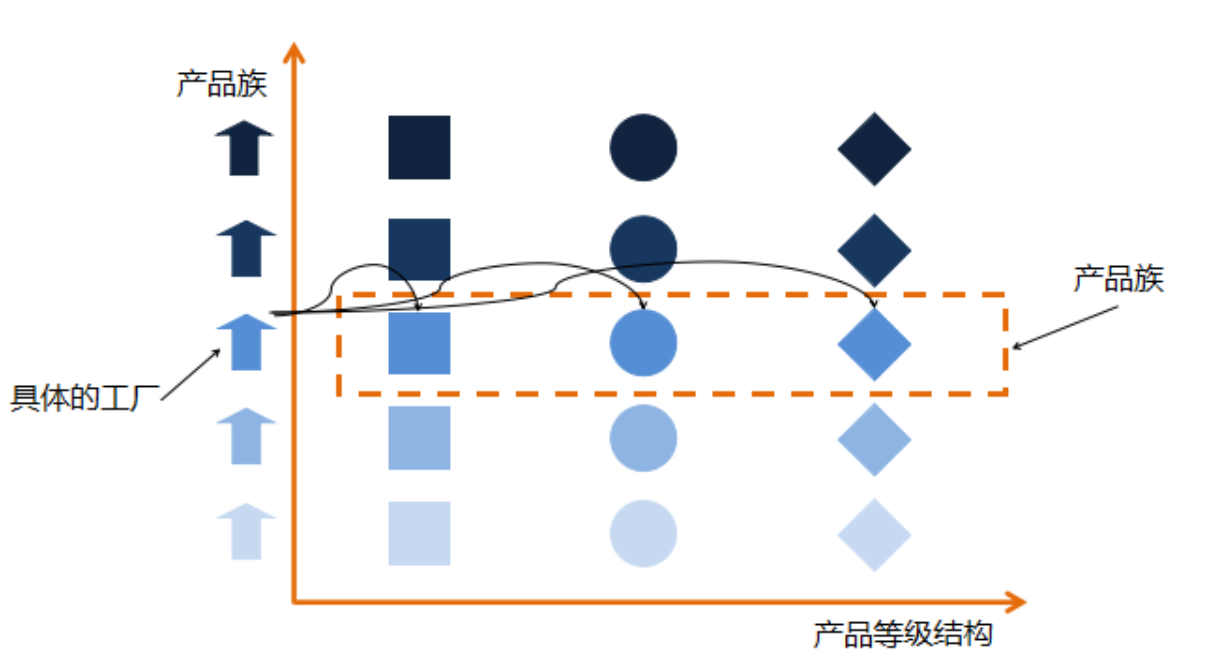
2_工厂设计_工厂方法和抽象工厂
工厂设计模式-工厂方法 1.概念 工厂方法模式(Fatory Method Pattern ) 是指定义一个创建对象的接口,但让实现这个接口的类来决定实例化哪个类,工厂方法让类的实例化推迟到子类中进行。 在工厂方法模式中用户只需要关心所需产品对应的工厂,…...

k8s之pod进阶
1.k8s的pod重启策略 Always :不论正常退出还是非正常退出都重启deployment的yaml文件只能是always pod的yaml三种模式都可以。 OnFailure:只有状态码非0才会重启,正常退出不重启 Never:正常退出和非正常退出都不重启 容器的退…...
)
RTTI(运行时类型识别)
RTTI(运行时类型识别) 实验介绍 RTTI 全称 Run Time Type Identification,中文称为 “运行时类型识别”,在程序中使用 typeid 和 dynamic_cast 实现。RTTI 技术允许程序在运行时识别对象的类型。 知识点 typeiddynamic_castRTTI 技术typeid typeid 是 C++ 关键字,用于…...

19.Linux Shell任务控制
文章目录 Linux Shell任务控制1)信号通过键盘生成信号trap 命令捕获信号 2)在后台运行脚本命令后加 & 符使用nohub命令 3)作业控制4)调度优先级nice命令renice 命令 5)定时运行作业at定期执行命令reference 欢迎访问个人网络日志🌹🌹知行空间&#x…...

域名流量被劫持怎么办?如何避免域名流量劫持?
随着互联网不断发展,流量成为线上世界的巨大财富。然而一种叫做域名流量劫持的网络攻击,将会在不经授权的情况下控制或重定向一个域名的DNS记录,导致用户在访问一个网站时,被引导到另一个不相关的网站,从而劫持走原网站…...

java案例知识点
一.会话技术 概念 技术 二.跨域 三.过滤器 四.拦截器...

Arrays 的使用
Arrays 概述 提供了数组操作的相关方法,连接数组和集合 asList 返回指定数组的列表列表和数组的引用位置相同 Integer[] arrs new Integer[] {1,2,3,4,5,6,7,8,9};List<Integer> list Arrays.asList(arrs);System.out.println(list);arrs[5] 100;Syste…...
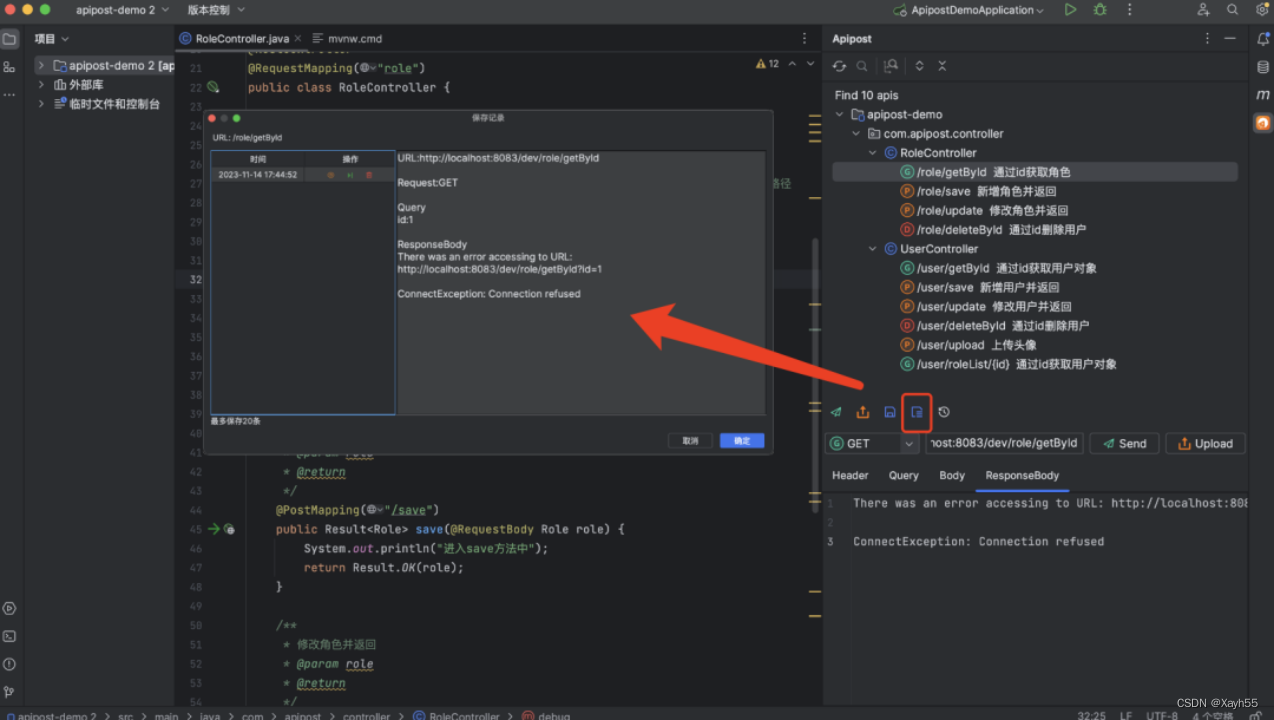
IDEA中怎么用Postman?这款插件你试试
Postman是大家最常用的API调试工具,那么有没有一种方法可以不用手动写入接口到Postman,即可进行接口调试操作?今天给大家推荐一款IDEA插件:Apipost Helper,写完代码就可以调试接口并一键生成接口文档!而且还…...
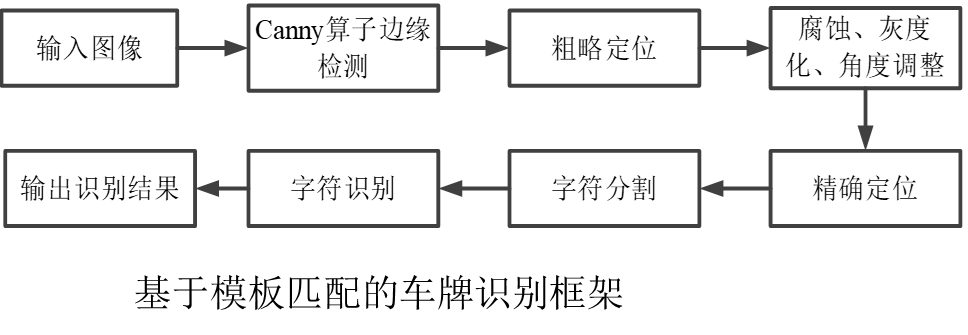
基于机器视觉的车牌检测-边缘检测因子的选择
车牌检测概述 车牌识别在检测报警、汽车出入登记、交通违法违章以及移动电子警察方面应用广泛。车牌识别过程为:首先通过摄像头获取包含车牌的彩色图像;然后进行车牌边缘检测,先粗略定位到车牌位置,再精细定位;最后根…...
学习c语言,变种水仙花
利用函数次方pow...
K8S--持久卷(PersistentVolume)的用法
原文网址:K8S--持久卷(PersistentVolume)的用法-CSDN博客 简介 本文介绍K8S的持久卷(PersistentVolume)的用法。 目标:用持久卷的方式将主机的磁盘与容器磁盘映射,安装nginx并运行。 --------------------------------------------------…...
书生·浦语大模型趣味 Demo笔记及作业
文章目录 笔记作业基础作业:进阶作业: 笔记 书生浦语大模型InternLM-Chat-7B 智能对话 Demo:https://blog.csdn.net/m0_49289284/article/details/135412067书生浦语大模型Lagent 智能体工具调用 Demo:https://blog.csdn.net/m0_…...

2024最新前端源码分享(附效果图及在线演示)
分享10款非常有趣的前端特效源码 其中包含css动画特效、js原生特效、svg特效以及小游戏等 下面我会给出特效样式图或演示效果图 但你也可以点击在线预览查看源码的最终展示效果及下载源码资源 粒子文字动画特效 基于canvas实现的粒子文字动画特效 会来回切换设定的文字特效 图…...

Microsoft 365 for Mac激活版(原Office 365)
Microsoft 365 for Mac原office 365,包含Word、Excel、PowerPoint 和 Outlook应用程序,协作办公的最佳首选。 软件下载:Microsoft 365 for Mac激活版下载 Microsoft 365 的一些主要功能包括: office 应用程序:Microsof…...

快乐学Python,Python基础之组织代码「类与对象」
在上一篇文章中,我们了解了函数。这一篇文章我们来了解一下Python中另外一个重要的概念:类与对象。 1、类与对象 (1)类与对象有什么关系? 你可能会奇怪,为什么要叫类与对象呢?是两个不同的东…...

H5的3D游戏开源框架
在H5的3D游戏框架中,Three.js、Babylon.js和Turbulenz是比较受欢迎的选择。 Three.js是一个广泛应用并且功能强大的JavaScript 3D库,可以创建简单的3D动画到创建交互的3D游戏。 Babylon.js是David Catuhe对3D游戏引擎热爱的结果,是最好的Ja…...

浅谈一些生命周期
vue2生命周期 beforeCreate :实例创建之初 created:组件已经创建完成 beforeMount:组件挂载之前 mounted:组件挂载之后 beforeUpdate:数据发生变化 更新之前 undated:数据发生之后 beforeDestroy :实…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...
