半监督学习 - 半监督聚类(Semi-Supervised Clustering)
什么是机器学习
半监督聚类是一种集成了有标签数据和无标签数据的聚类方法,其目标是在聚类的过程中利用有标签数据的信息来提高聚类性能。在半监督聚类中,一部分数据集有已知的标签,而另一部分没有标签。
以下是半监督聚类的基本思想和一些常见方法:
基本思想:
- 有标签数据: 利用有标签的数据对聚类过程进行监督或指导,以提高聚类的准确性。
- 无标签数据: 利用无标签的数据进行聚类,从中发现潜在的簇结构。
常见的半监督聚类方法:
- Constrained Clustering: 在这种方法中,用户提供一些先验的约束条件,如样本之间属于同一类或不属于同一类,以引导聚类过程。
- Self-training: 利用已有的有标签数据来初始化聚类模型,然后使用无标签数据进行训练,逐渐将无标签数据加入到已有的聚类中。
- Co-Training: 在半监督聚类中,Co-Training方法使用两个或多个视图或特征集,每个特征集对应一个模型。模型在一个视图上训练,然后通过对另一个视图上的数据进行预测来自我训练。
- Spectral Methods: 基于谱聚类的方法也可以用于半监督聚类。通过考虑已标签和未标签数据之间的关系,可以在谱聚类中引入先验信息。
- Generative Models: 一些生成模型,如深度生成对抗网络(GANs)或变分自编码器(VAEs),也可以用于半监督聚类,通过同时考虑有标签和无标签数据进行训练。
优点和注意事项
- 更充分利用数据: 半监督聚类充分利用了有标签和无标签数据,提高了聚类性能。
- 对领域知识的整合: 可以结合领域知识,通过约束或先验信息提高聚类的准确性。
- 依赖标签质量: 结果的质量依赖于有标签数据的质量,不准确的标签可能影响聚类效果。
- 选择合适的方法: 不同的半监督聚类方法适用于不同的场景,需要根据具体问题选择合适的方法。
半监督聚类是一个复杂的问题,有许多不同的方法可供选择,具体选择取决于数据的性质、标签的质量以及任务的要求。
相关文章:
)
半监督学习 - 半监督聚类(Semi-Supervised Clustering)
什么是机器学习 半监督聚类是一种集成了有标签数据和无标签数据的聚类方法,其目标是在聚类的过程中利用有标签数据的信息来提高聚类性能。在半监督聚类中,一部分数据集有已知的标签,而另一部分没有标签。 以下是半监督聚类的基本思想和一些…...
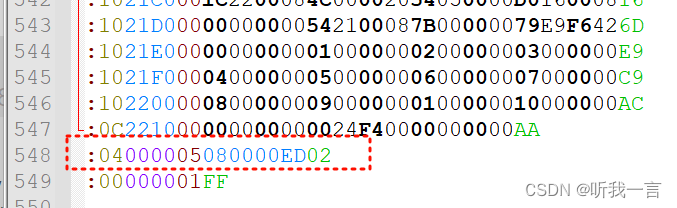
实现STM32烧写程序-(3) Hex文件结构
简介 要对STM32进行更新动作, 就需要对程序文件进行解析, 大部分编译的生成程序文件是Hex或者Bin, 先来看看Hex的结构吧。 资料 Hex文件 简介 Hex文件格式最早由Intel公司于1973年创建。它最初是为了在Intel 8080微处理器上存储和传输二进制数据而设计的。随后,Hex…...
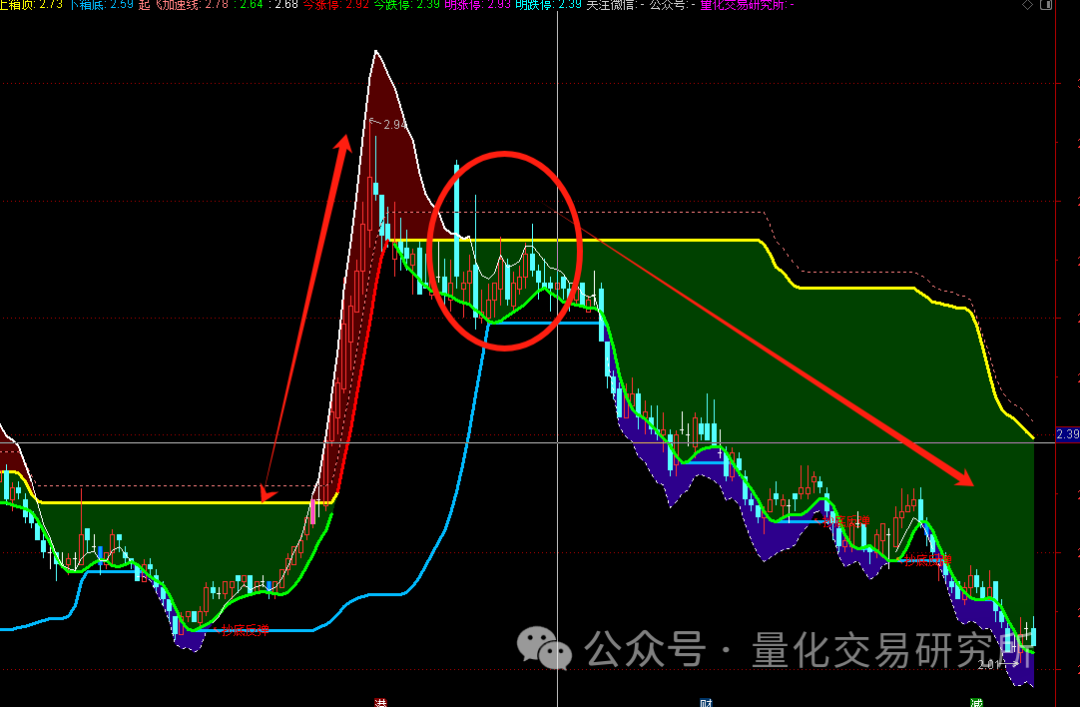
精品量化公式——“区域突破”,应对当下行情较好的主图看盘策略
不多说,直接上效果如图: ► 日线表现 代码评估 技术指标代码评估: VAR1, VAR2, VAR3:这些变量是通过指数移动平均(EMA)计算得出的。EMA是一种常用的技术分析工具,用于平滑价格数据并减少市场“…...

自然语言处理5——发掘隐藏规律 - Python中的关联规则挖掘
目录 写在开头1. 了解关联规则挖掘的概念和实际应用1.1 关联规则挖掘在市场分析和购物篮分析中的应用1.2 关联规则的定义和基本原理1.3 应用场景2. 使用Apriori算法和FP-growth算法进行关联规则挖掘2.1 Apriori算法的工作原理和实现步骤2.2 FP-growth算法的优势和使用方法2.3 A…...

【记录】重装系统后的软件安装
考完研重装了系统,安装软件乱七八糟,用到什么装什么。在这里记录一套标准操作,备用。一个个装还是很麻烦,我为什么不直接写个脚本直接下载安装包呢?奥,原来是我太菜了还不会写脚本啊!先记着吧&a…...
- ACodec(七))
Android 13 - Media框架(31)- ACodec(七)
之前的章节中我们解了 input buffer 是如何传递给 OMX 的,以及Output buffer 是如何分配并且注册给 OMX 的。这一节我们就来看ACodec是如何处理OMX的Callback的。 1、OMXNodeInstance Callback 这一节我们只大致记录Callback是如何传递给ACodec的。在之前的学习中我…...

快速了解VR全景拍摄技术运用在旅游景区的优势
豆腐脑加了糖、烤红薯加了勺,就连索菲亚大教堂前都有了“人造月亮”,在这个冬季,“尔滨”把各地游客宠上了天。面对更多的游客无法实地游玩,哈尔滨冰雪世界再添新玩法,借助VR全景拍摄技术对冬季经典冰雪体验项目进行全…...

分布形态的度量_峰度系数的探讨
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还应掌握数据分布的形态。 描述数据分布形态的度量有偏度系数和峰度系数, 其中偏度系数描述数据的对称性,峰度系数描述与正态分布的偏离程度。 峰度系数反映分布峰的尖峭程度的重要指标. 当…...
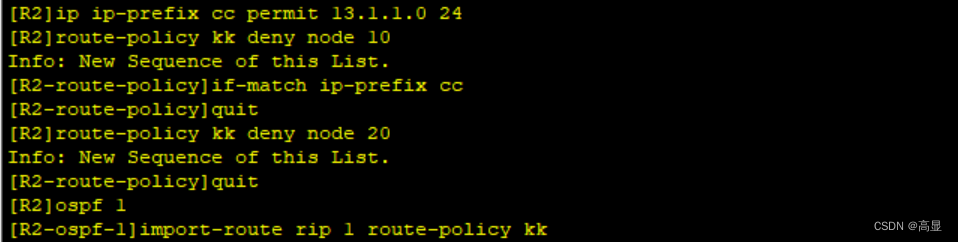
HCIP 重发布
拓扑图&IP划分如下: 第一步,配置接口IP&环回地址 以R1为例,R2~R4同理 interface GigabitEthernet 0/0/0 ip address 12.1.1.1 24 interface GigabitEthernet 0/0/1 ip address 13.1.1.1 24 interface LoopBack 0 ip address 1.1.1.…...

FX图中的节点代表什么操作
在 FX 图中,每个节点代表一个操作。这些操作可以是函数调用、方法调用、模块实例调用,也可以是 torch.nn.Module 实例的调用。每个节点都对应一个调用站点,如运算符、方法和模块。 一.节点操作 下面是一些节点可能代表的操作: 1…...

【Java 设计模式】创建型之单例模式
文章目录 1. 定义2. 应用场景3. 代码实现1)懒汉式2)饿汉式 4. 应用示例结语 在软件开发中,单例模式是一种常见的设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式在需要控制某些资源,如数…...
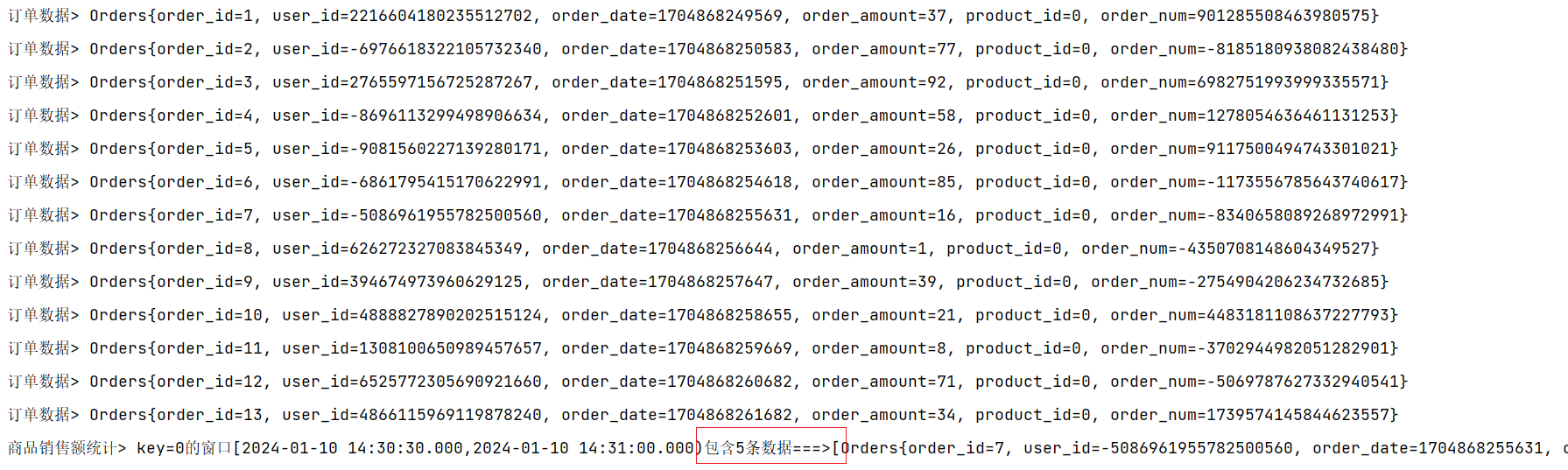
FlinkAPI开发之窗口(Window)
案例用到的测试数据请参考文章: Flink自定义Source模拟数据流 原文链接:https://blog.csdn.net/m0_52606060/article/details/135436048 窗口的概念 Flink是一种流式计算引擎,主要是来处理无界数据流的,数据源源不断、无穷无尽。…...
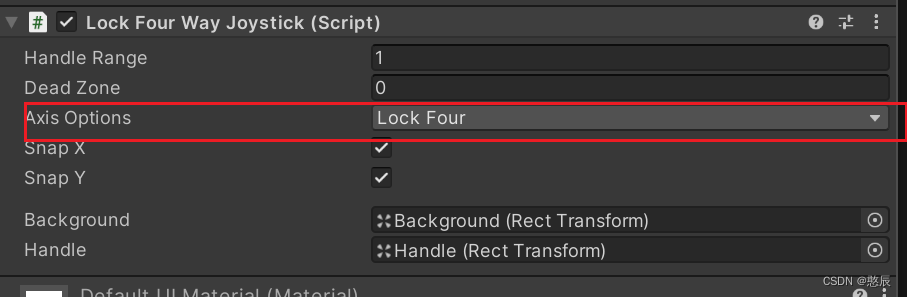
【Unity】Joystick Pack摇杆插件实现锁四向操作
Joystick Pack 简介:一款Unity摇杆插件,非常轻量化 摇杆移动类型:圆形、横向、竖向 摇杆类型: Joystick描述Fixed固定位置Floating浮动操纵杆从用户触碰的地方开始,一直固定到触碰被释放。Dynamic动态操纵…...

29 旋转工具箱
效果演示 实现了一个菜单按钮的动画效果,当鼠标悬停在菜单按钮上时,菜单按钮会旋转315度,菜单按钮旋转的同时,菜单按钮旋转的8个小圆圈也会依次旋转360度,并且每个小圆圈的旋转方向和菜单按钮的旋转方向相反࿰…...
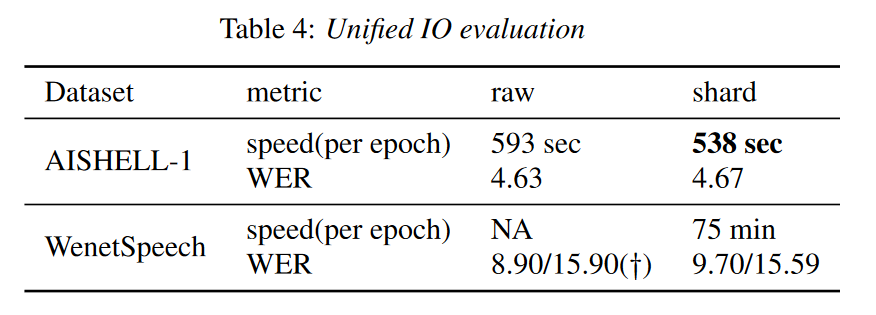
WeNet2.0:提高端到端ASR的生产力
摘要 最近,我们提供了 WeNet [1],这是一个面向生产(工业生产环境需求)的端到端语音识别工具包,在单个模型中,它引入了统一的两次two-pass (U2) 框架和内置运行时(built-in runtime)…...
)
第九部分 使用函数 (四)
目录 一、foreach 函数 二、if 函数 三、call 函数 一、foreach 函数 foreach 函数和别的函数非常的不一样。因为这个函数是用来做循环用的,Makefile 中的 foreach 函数几乎是仿照于 Unix 标准 Shell(/bin/sh)中的 for 语句,或…...
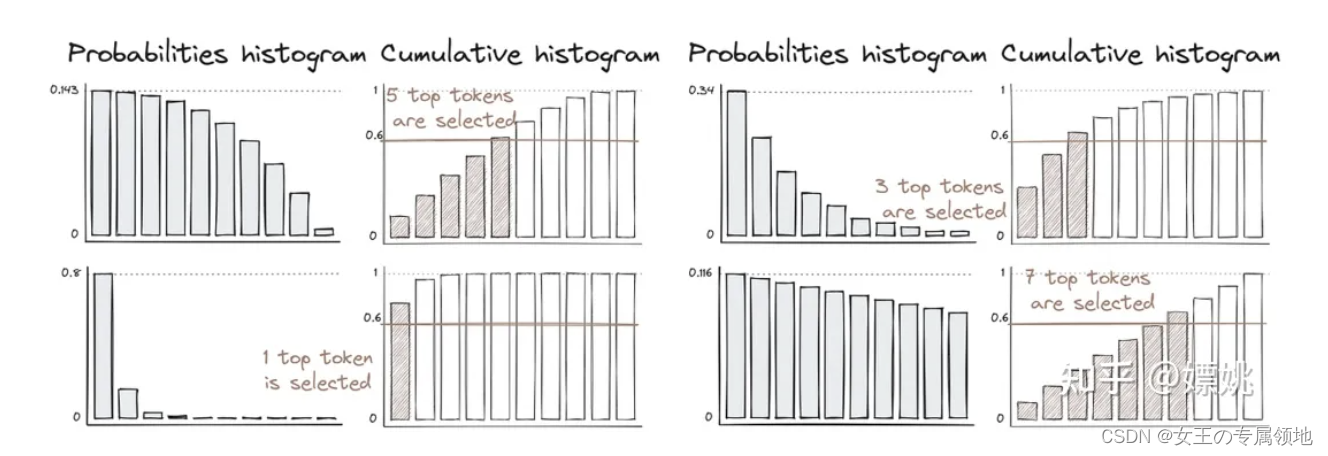
一文读懂「Prompt Engineering」提示词工程
在了解提示过程之前,先了解一下什么是提示prompt,见最后附录部分 一、什么是Prompt Engingering? 提示工程(Prompt Engingering),也被称为上下文提示(In-Context Prompting)&#x…...

微信小程序(一)简单的结构及样式演示
注释很详细,直接上代码 涉及内容: view和text标签的使用类的使用flex布局水平方向上均匀分布子元素垂直居中对齐子元素字体大小文字颜色底部边框的宽和颜色 源码: index.wxml <view class"navs"><text class"active…...

【设计模式】外观模式
前言 1. 单例模式(Singleton Pattern):保证一个类只有一个实例,并提供一个全局的访问点。 2. 工厂模式(Factory Pattern):定义一个创建对象的接口,但由子类决定要实例化的类是哪一…...
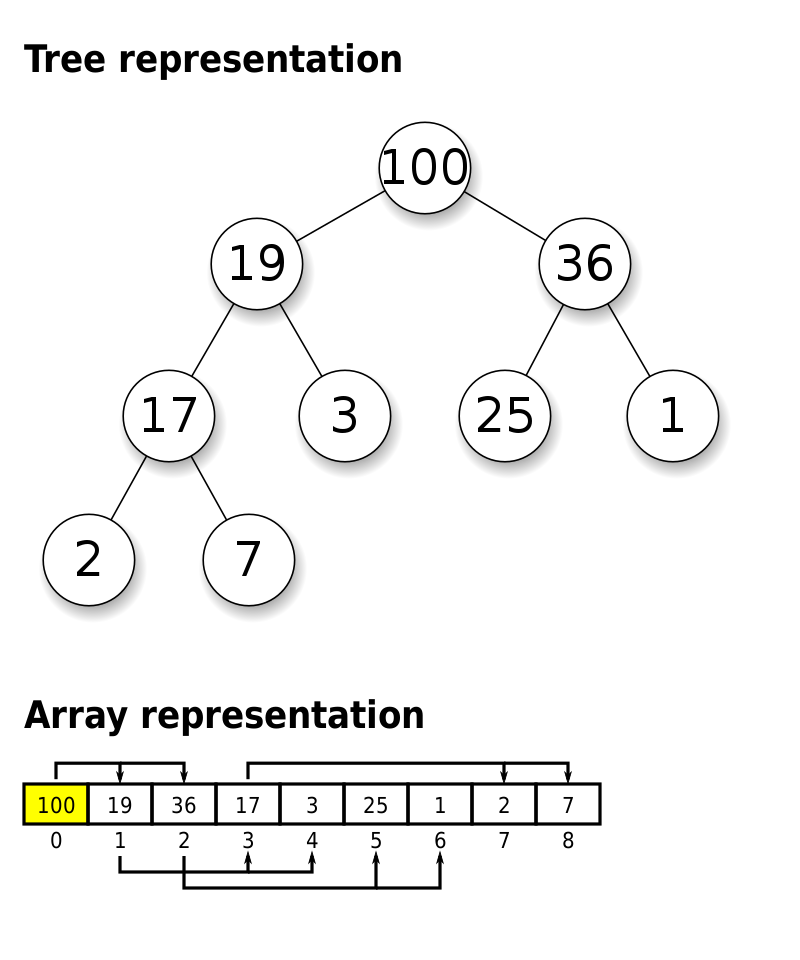
优先级队列(Priority Queue)
文章目录 优先级队列(Priority Queue)实现方式基于数组实现基于堆实现方法实现offer(E value)poll()peek()isEmpty()isFull() 优先级队列的实现细节 优先级队列(Priority Queue) 优先级队列是一种特殊的队列,其中的元素…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
