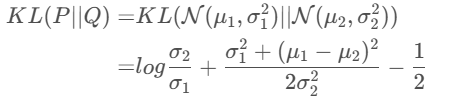VAE--part1
Variational Auto-Encoder, VAE__part1
- 分布变换
- VAE慢谈
- VAE 初现
- 分布标准化
- 重参数技巧
- VAE的本质是什么?
- VAE的本质结构
- 正态分布?
- 变分在哪里
参考博客仅做学习记录,侵删
分布变换
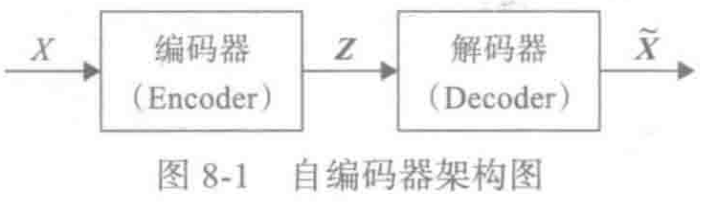
VAE和GAN都是生成式模型,它们俩的目标基本一致:希望构建一个从隐变量Z,来生成目标数据X的模型,但实现上有所不同。
更准确地讲,它们是假设Z服从了某些常见的分布(比如:正态分布或均匀分布),然后希望训练一个模型X=g(Z), g为生成器generator, 这个模型可以将原来的概率分布映射到训练集的概率分布,即,它们的目的都是进行分布之间的变换。
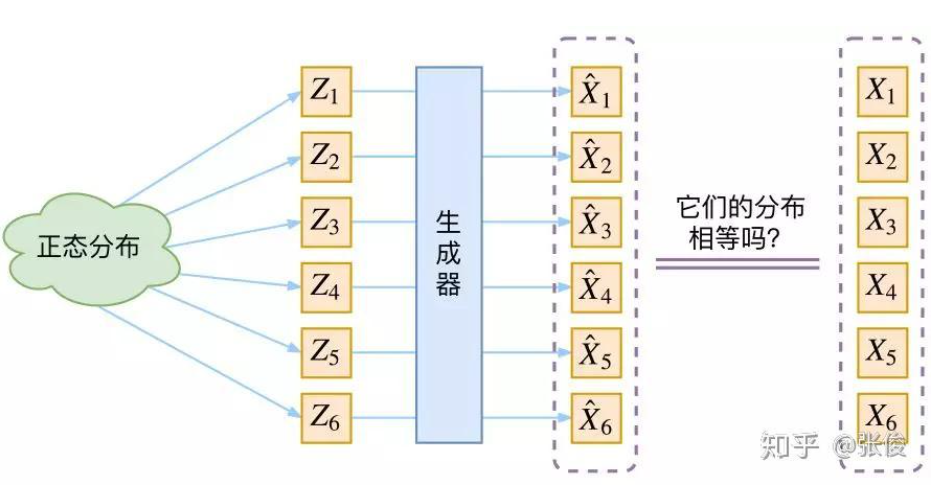
生成模型的难题就是判断生成分布与真实分布的相似度,因为我们只知道两者的采样结果,不知道它们的分布表达式。
那现在假设 Z 服从标准的正态分布,那我们就可以从中采样得到若干个 Z1,Z2,Z3,⋯,ZnZ_{1}, Z_{2}, Z_{3},\cdots, Z_{n}Z1,Z2,Z3,⋯,Zn, 然后输入到生成器中,得到X^1=g(Z1),X^2=g(Z2),⋯X^n=g(Zn)\hat{X}_{1}=g(Z_{1}), \hat{X}_{2}=g(Z_{2}), \cdots\hat{X}_{n}=g(Z_{n})X^1=g(Z1),X^2=g(Z2),⋯X^n=g(Zn), 我们怎么判断这个通过 ggg 构造出来的数据集,它的分布跟我们目标的数据集分布是不是一样的呢?
思考:
Q1:KL散度用来衡量两个分布之间的相似度,用KL散度可以吗?
答:不行,因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的,然而目前我们并不知道它们的概率分布的表达式。
我们只有一批从构造的分布采样而来的数据{X^1,X^2,X^3,⋯,X^n\hat{X}_{1}, \hat{X}_{2}, \hat{X}_{3},\cdots, \hat{X}_{n}X^1,X^2,X^3,⋯,X^n}, 还有一批从真实的分布采样而来的数据{X1,X2,X3,⋯,XnX_{1}, X_{2}, X_{3},\cdots, X_{n}X1,X2,X3,⋯,Xn}, 即训练集,我们只有样本本身,没有分布表达式,当然也就没有办法算 KL 散度。
虽然遇到困难,但还是要想办法解决的。GAN 的思路很直接粗犷:既然没有合适的度量,那我干脆把这个度量也用神经网络训练出来吧。
VAE慢谈
首先我们有一批数据样本{X1,X2,⋯,XnX_{1}, X_{2}, \cdots, X_{n}X1,X2,⋯,Xn},其整体用 X 来描述,我们本想根据{X1,X2,⋯,XnX_{1}, X_{2}, \cdots, X_{n}X1,X2,⋯,Xn}得到 X 的分布 p(X), 如果能得到的话,那我直接根据 p(X) 来采样,这样就可以得到所有的 X 了(包括{X1,X2,⋯,XnX_{1}, X_{2}, \cdots, X_{n}X1,X2,⋯,Xn}之外的 XiX_{i}Xi), 这是一个终极理想的生成模型了。
当然,这个理想很难实现,于是我们将分布改一改:
p(X)=∑Zp(X∣Z)p(Z)①p(X)=\sum_{Z}p(X|Z)p(Z)\quad\quad①p(X)=Z∑p(X∣Z)p(Z)①
这里我们就不区分求和还是求积分了,意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X的模型,而我们假设 Z 服从标准正态分布,也就是 p(Z)=N(0,I)p(Z)=N(0,I)p(Z)=N(0,I)。如果这个理想能实现,那么我们就可以先从标准正态分布中采样一个 Z,然后根据 Z 来算一个 X,也是一个很棒的生成模型。
接下来就是结合自编码器来实现重构,保证有效信息没有丢失,再加上一系列的推导,最后把模型实现。框架的示意图如下:
上图的疑惑所在:
对于上图的话,我们其实完全不清楚:究竟经过重新采样出来的ZkZ_{k}Zk,是不是还对应着原来的 XkX_kXk,所以我们如果直接最小化 D(X^k,Xk)2D(\hat{X}_k, X_k)^2D(X^k,Xk)2(这里 D 代表某种距离函数)是很不科学的,而事实上你看代码也会发现根本不是这样实现的。
VAE 初现
其实,在整个 VAE 模型中,我们并没有去使用 p(Z)(先验分布)是正态分布的假设,我们用的是假设 p(Z|X)(后验分布)是正态分布。
具体来说,给定一个真实样本 XkX_kXk,我们假设存在一个专属于 XkX_kXk 的分布 p(Z∣Xk)p(Z|X_k)p(Z∣Xk)(学名叫后验分布),并进一步假设分布 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 是(独立的、多元的)正态分布。
为什么要强调“专属”呢?因为我们后面要训练一个生成器 X=g(Z),希望能够把从分布 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 采样出来的一个 ZkZ_kZk 还原为 XkX_kXk。
如果假设 p(Z) 是正态分布,然后从 p(Z) 中采样一个 Z,那么我们怎么知道这个 Z 对应于哪个真实的 X 呢?现在 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 专属于 XkX_kXk,我们有理由说从这个分布采样出来的 Z 应该要还原到 XkX_kXk 中去。
事实上,在论文 Auto-Encoding Variational Bayes 的应用部分,也特别强调了这一点:
In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:
logqϕ(z∣xi)=logN(z;μi,σi2I)②\log q_{\phi}(z|x_{i})=\log N(z;\mu_{i}, \sigma^{2}_{i}I)\quad②logqϕ(z∣xi)=logN(z;μi,σi2I)②
论文中的上式是实现整个模型的关键,不知道为什么很多教程在介绍 VAE 时都没有把它凸显出来。尽管论文也提到 p(Z) 是标准正态分布,然而那其实并不是本质重要的。
再次强调,这时候每一个 XkX_kXk 都配上了一个专属的正态分布,才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数:均值 μ\muμ 和方差 σ2\sigma^{2}σ2(如果X为向量的话,则μ\muμ 和σ2\sigma^{2}σ2都是向量)。
那怎么找出专属于 XkX_kXk 的正态分布 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 的均值和方差呢?好像并没有什么直接的思路。
好吧,就用神经网络来拟合出来。这就是神经网络时代的哲学:难算的我们都用神经网络来拟合,在 WGAN 那里我们已经体验过一次了,现在再次体验到了。
于是我们构建了两个神经网络 μk=f1(Xk),logσ2=f2(Xk)\mu_{k}=f_{1}(X_{k}), \log \sigma^{2}= f_{2}(X_{k})μk=f1(Xk),logσ2=f2(Xk)来求 μ\muμ 和 σ\sigmaσ。我们选择拟合 logσ2\log \sigma^{2}logσ2, 而不是直接拟合 σ2\sigma^{2}σ2, 是因为 σ2\sigma^{2}σ2 总是非负的,需要加激活函数处理,而拟合 logσ2\log \sigma^{2}logσ2 不需要加激活函数,因为它可正可负。
具体这个是咋用神经网络去求μ,σ\mu,\sigmaμ,σ呢?可以参看下图
或者可以去看这篇博客:用VAE生成图像会得到更深刻的理解
到这里,我能知道专属于 XkX_kXk 的均值和方差了,也就知道它的正态分布长什么样了,然后从这个专属分布中采样一个 ZkZ_kZk 出来,然后经过一个生成器得到 X^k=g(Zk)X̂_k=g(Z_k)X^k=g(Zk)。
其实就是:
Zk=μ+ϵ∗σ,ϵ∼N(0,1)③Z_{k} = \mu + \epsilon*\sigma,\quad\quad\epsilon\sim N(0,1)\quad\quad③Zk=μ+ϵ∗σ,ϵ∼N(0,1)③
也可以写成:Zk=μ+ϵ∗e12.logσ2,ϵ∼N(0,1)④Z_{k} = \mu + \epsilon*e^{\frac{1}{2}.\log \sigma^2},\quad\quad\epsilon\sim N(0,1)\quad④Zk=μ+ϵ∗e21.logσ2,ϵ∼N(0,1)④,这俩式子本质都是一样的。
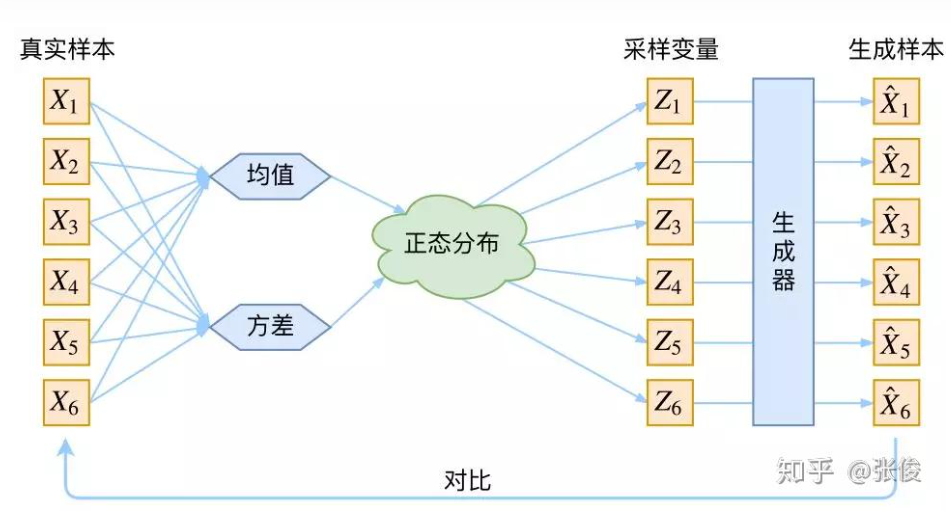
现在我们可以放心地最小化 D(X^k,Xk)2D(X̂_k,X_k)^2D(X^k,Xk)2,因为 ZkZ_kZk 是从专属 XkX_kXk 的分布中采样出来的,这个生成器应该要把开始的 XkX_kXk 还原回来。于是可以画出 VAE 的示意图:
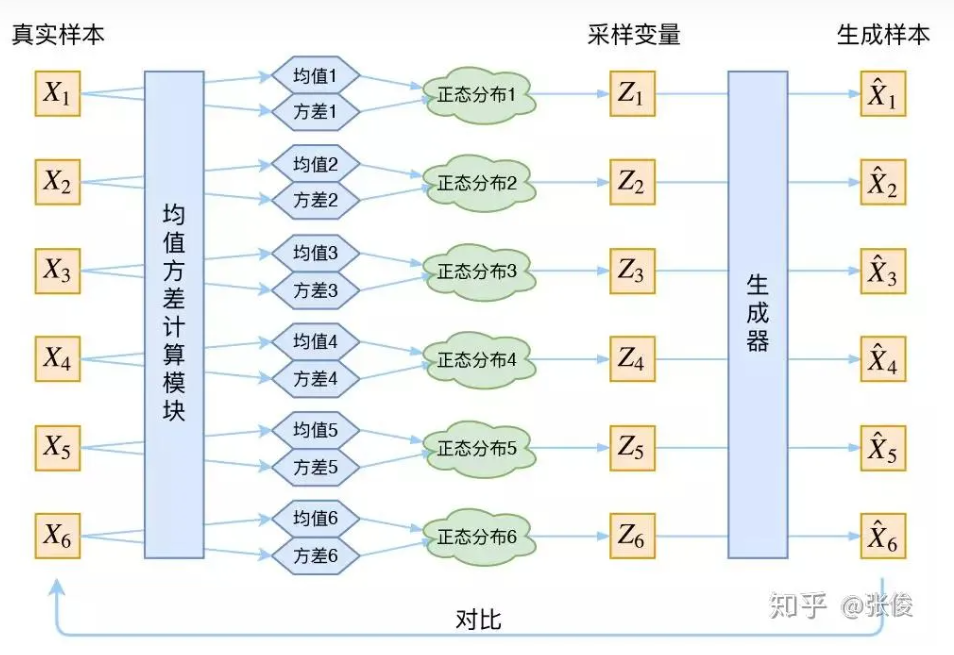
事实上,VAE 是为每个样本构造专属的正态分布,然后采样来重构。
分布标准化
让我们来思考一下,根据上图的训练过程,最终会得到什么结果。
首先,我们希望重构 X,也就是最小化 D(X^k,Xk)2D(X̂_k,X_k)^2D(X^k,Xk)2,但是这个重构过程受到噪声的影响,因为 ZkZ_kZk 是通过重新采样过的,即上面式子③Zk=μ+ϵ∗σ,ϵ∼N(0,1)Z_{k} = \mu + \epsilon*\sigma,\quad\epsilon\sim N(0,1)Zk=μ+ϵ∗σ,ϵ∼N(0,1),不是直接由 encoder 算出来的,直接由encoder算出来的是μ,σ\mu, \sigmaμ,σ(或者logσ2\mathrm{\log \sigma^2}logσ2)。
显然噪声会增加重构的难度,不过好在这个噪声强度(也就是方差σ\sigmaσ)通过一个神经网络算出来的,所以最终模型为了重构得更好,肯定会想尽办法让方差为0。即让这个Z 更接近 X。
但是由Zk=μ+ϵ∗σ,ϵ∼N(0,1)Z_{k} = \mu + \epsilon*\sigma,\quad\epsilon\sim N(0,1)Zk=μ+ϵ∗σ,ϵ∼N(0,1)可知,当σ=0\sigma=0σ=0时,也就没有随机性了,即固定有Z=μZ=\muZ=μ,所以不管怎样采样其实都只是得到确定的结果(也就是均值μ\muμ),只拟合一个当然比拟合多个要容易,而均值是通过另外一个神经网络算出来的。
说白了,模型会慢慢退化为普通的AE(autoEncoder),噪声不再起作用。
但是自编码器AE不能随意产生合理的潜在变量,从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。这样不就白费力气了吗?说好的生成模型呢?
别急别急,其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐,这样就防止了噪声为零,同时保证了模型具有生成能力。即不能都是Z=μZ=\muZ=μ,
那为什么这样就可以保证“生成能力”了呢? 如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I),那么根据定义:
p(Z)=∑Xp(Z∣X)p(X)=∑XN(0,I)p(X)=N(0,I)∑Xp(X)=N(0,I)⑤p(Z)=\sum_{X}p(Z|X)p(X)=\sum_{X}N(0,I)p(X)=N(0,I)\sum_{X}p(X)=N(0,I)\quad⑤p(Z)=X∑p(Z∣X)p(X)=X∑N(0,I)p(X)=N(0,I)X∑p(X)=N(0,I)⑤
这样我们就能达到我们的先验假设:p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。
为什么符合先验假设p(Z)是标准正态分布,就可以放心从N(0,I)中采样生成图像了呢?
答:个人理解是:如下图中的{Z1,Z2⋯,Z6Z_1,Z_2\cdots,Z_6Z1,Z2⋯,Z6}都是从N(0,I)中采样得到的,然后通过生成器可以得到{X1^,X2^,⋯X6^\hat{X_1},\hat{X_2},\cdots\hat{X_6}X1^,X2^,⋯X6^}(假设已经经过训练好了),那就是说训练后我们认为训练的还不错,即Xi^≈Xi\hat{X_i}\approx X_iXi^≈Xi,即生成样本和真实样本很像,即符合真实样本的分布。这个时候拿训练好的模型,然后从标准正态分布N(0,I)中随机采样Z,然后inference得到生成的样本也就可以认为是符合真实样本的分布了。
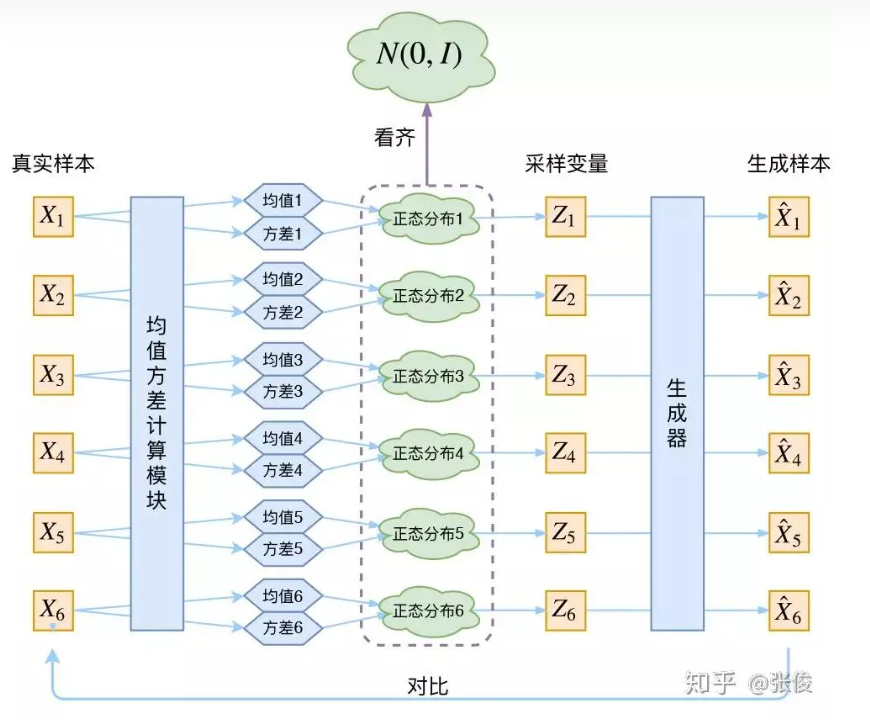
为了使模型具有生成能力,VAE要求每个p(Z|X)都向正态分布看齐。
那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢?如果没有外部知识的话,其实最直接的方法应该是在重构误差的基础上中加入额外的 loss:
Lμ=∥f1(Xk)∥2⑥\mathcal{L}_{\mu}=\left\|f_{1}\left(X_{k}\right)\right\|^{2} \quad ⑥Lμ=∥f1(Xk)∥2⑥
Lσ2=∥f2(Xk)∥2⑦\mathcal{L}_{\sigma^{2}}=\left\|f_{2}\left(X_{k}\right)\right\|^{2}\quad⑦Lσ2=∥f2(Xk)∥2⑦
因为它们分别代表了均值μk\mu_kμk和方差的对数logσ2\log \sigma^2logσ2, 达到N(0,I)就是希望Lμ\mathcal{L}_{\mu}Lμ和Lσ2\mathcal{L}_{\sigma^{2}}Lσ2尽量接近于0。不过,这又会面临着这两个损失的比例要怎么选取的问题,选取得不好,生成的图像会比较模糊。
说明:
1.希望Lμ\mathcal{L_{\mu}}Lμ尽量接近于0
首先要知道f1(Xk)f_{1}(X_{k})f1(Xk)就是指:用神经网络求出来的μ\muμ,那自然是希望μ\muμ越接近0了。
2.为啥希望Lσ2\mathcal{L}_{\sigma^{2}}Lσ2也尽量接近于0呢?
f1(Xk)f_{1}(X_{k})f1(Xk)就是指:用神经网络求出来的logσ2\log \sigma^2logσ2。
因为是希望σ≈1\sigma\approx1σ≈1, 那就是logσ2≈0\log \sigma^2\approx0logσ2≈0。
所以,原论文直接算了一般(各分量独立的)正态分布与标准正态分布的 KL 散度 KL(N(μ,σ2)‖N(0,I))KL(N(μ,σ^2)‖N(0,I))KL(N(μ,σ2)‖N(0,I)) 作为这个额外的 loss,计算结果为:
Lμ,σ2=12∑i=1d(μ(i)2+σ(i)2−logσi2−1)⑧\mathcal{L}_{\mu,\sigma^2}=\frac{1}{2}\sum_{i=1}^{d}(\mu_{(i)}^{2}+\sigma_{(i)}^{2}-\log \sigma_{i}^{2}-1)\quad⑧Lμ,σ2=21i=1∑d(μ(i)2+σ(i)2−logσi2−1)⑧
这里的 d 是隐变量 Z 的维度,而 μ(i)μ_{(i)}μ(i) 和 σ(i)2σ_{(i)}^{2}σ(i)2 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss,就不用考虑均值损失和方差损失的相对比例问题了。
显然,这个loss也可以分为两部分理解:
Lμ,σ2=Lμ+Lσ2⑨\mathcal{L}_{\mu, \sigma^2}=\mathcal{L_{\mu}+L_{\sigma^2}}\quad⑨Lμ,σ2=Lμ+Lσ2⑨
Lμ=12∑i=1dμ(i)2=12∥f1(X)∥2⑩\mathcal{L_{\mu}}=\frac{1}{2}\sum_{i=1}^{d}\mu_{(i)}^{2}=\frac{1}{2}\left\|f_{1}\left(X\right)\right\|^{2}\quad⑩Lμ=21i=1∑dμ(i)2=21∥f1(X)∥2⑩
Lσ2=12∑i=1d(σ(i)2−logσ(i)2−1)\mathcal{L_{\sigma^{2}}}=\frac{1}{2}\sum_{i=1}^{d}(\sigma_{(i)}^2-\log \sigma_{(i)}^2 - 1)Lσ2=21i=1∑d(σ(i)2−logσ(i)2−1)
说明:
式⑧的由来:
具体可以见高斯分布的KL散度了解详细推导过程
重参数技巧
Reparameterization Trick
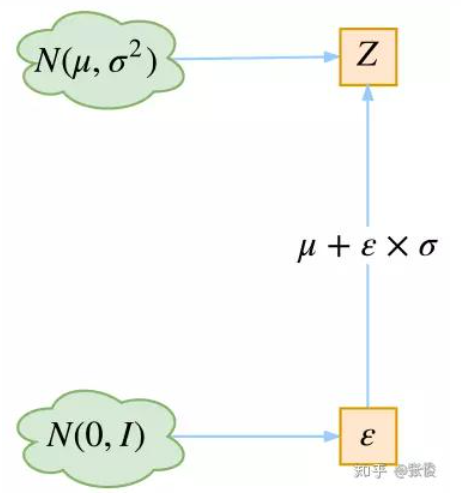
其实很简单,就是我们要从 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 中采样一个 ZkZ_kZk 出来,尽管我们知道了 p(Z∣Xk)p(Z|X_k)p(Z∣Xk) 是正态分布,但是均值方差都是靠模型算出来的,我们要靠这个过程反过来优化均值方差的模型,但是“采样”这个操作是不可导的,而采样的结果是可导的,于是我们利用了一个事实:
从N(μ,σ2)N(\mu, \sigma^2)N(μ,σ2)中采样一个Z, 相当于从N(0,I)N(0,I)N(0,I)中采样一个ϵ\epsilonϵ, 然后让Z=μ+ϵ∗σZ=\mu + \epsilon * \sigmaZ=μ+ϵ∗σ
所以,我们将从 N(μ,σ2)N(μ,σ^2)N(μ,σ2)
采样变成了从 N(0,I)N(0 ,I)N(0,I)
中采样,然后通过参数变换得到从N(μ,σ2)N(μ,σ^2)N(μ,σ2) 中采样的结果。这样一来,“采样”这个操作就不用参与梯度下降了,改为采样的结果参与,使得整个模型可训练了。
具体可以参看这篇博客

VAE的本质是什么?
VAE 的本质是什么?VAE 虽然也称是 AE(AutoEncoder)的一种,但它的做法(或者说它对网络的诠释)是别具一格的。
在 VAE 中,它的 Encoder 有两个,一个用来计算均值,一个用来计算方差,这已经让人意外了:Encoder 不是用来 Encode 的,是用来算均值和方差的,这真是大新闻了,还有均值和方差不都是统计量吗,怎么是用神经网络来算的?
VAE 从让普通人望而生畏的变分和贝叶斯理论出发,最后落地到一个具体的模型中,虽然走了比较长的一段路,但最终的模型其实是很接地气的。
它本质上就是在我们常规的自编码器的基础上,对 encoder 的结果(在VAE中对应着计算均值的网络)加上了“高斯噪声”,使得结果 decoder 能够对噪声有鲁棒性;而那个额外的 KL loss(目的是让均值为 0,方差为 1),事实上就是相当于对 encoder 的一个正则项,希望 encoder 出来的东西均有零均值。
那另外一个 encoder(对应着计算方差σ\sigmaσ的网络)的作用呢?它是用来动态调节噪声的强度的。
直觉上来想,当 decoder 还没有训练好时(重构误差远大于 KL loss),就会适当降低噪声(KL loss 增加),使得拟合起来容易一些(重构误差开始下降)。
反之,如果 decoder 训练得还不错时(重构误差小于 KL loss),这时候噪声就会增加(KL loss 减少),使得拟合更加困难了(重构误差又开始增加),这时候 decoder 就要想办法提高它的生成能力了。
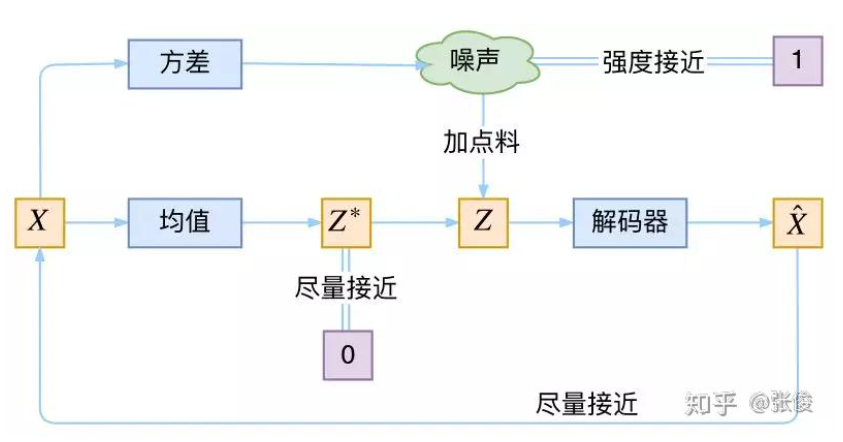
VAE的本质结构
说白了,重构的过程是希望没噪声的,而 KL loss 则希望有高斯噪声的,两者是对立的。所以,VAE 跟 GAN 一样,内部其实是包含了一个对抗的过程,只不过它们两者是混合起来,共同进化的。
说明:
重构:即训练的过程中,从XaX_{a}Xa到Z再到XbX_{b}Xb,自然是希望Z能稳定下来为一个定值,这样恢复出来的XbX_{b}Xb就更具有确定性,更能接近真实样本XaX_{a}Xa。
KL loss: 因为我们训练的目的就是为了让模型有生成能力,即从噪声出发,通过模型来生成符合真是样本分布的新样本。如果我们在训练过程中让Z稳定下来为一个定值,那我们在inference的时候就不能从噪声出发了。
因为我们最终的目的是:拿训练好的模型,然后从标准正态分布N(0,I)中随机采样Z,然后inference得到生成的样本也就可以认为是符合真实样本的分布了,所以我们并不能真的让Z为一个定值固定下来。这样用含有噪声的Z去生成Xi^\hat{X_{i}}Xi^, 然后来衡量生成数据Xi^的分布\hat{X_{i}}的分布Xi^的分布与原始数据XiX_{i}Xi的分布之间的相似度,自然是越相似越好。
可以结合前面这个问题:**为什么符合先验假设p(Z)是标准正态分布,就可以放心从N(0,I)中采样生成图像了呢?**来进行思考。
正态分布?
对于 p(Z|X) 的分布,读者可能会有疑惑:是不是必须选择正态分布?可以选择均匀分布吗?
首先,这个本身是一个实验问题,两种分布都试一下就知道了。但是从直觉上来讲,正态分布要比均匀分布更加合理,因为正态分布有两组独立的参数:均值和方差,而均匀分布只有一组。
前面我们说,在 VAE 中,重构跟噪声是相互对抗的,重构误差跟噪声强度是两个相互对抗的指标,而在改变噪声强度时原则上需要有保持均值不变的能力,不然我们很难确定重构误差增大了,究竟是均值变化了(encoder的锅)还是方差变大了(噪声的锅)。
而均匀分布不能做到保持均值不变的情况下改变方差,所以正态分布应该更加合理。
变分在哪里
还有一个有意思(但不大重要)的问题是:VAE 叫做“变分自编码器”,它跟变分法有什么联系?在VAE 的论文和相关解读中,好像也没看到变分法的存在?
其实如果读者已经承认了 KL 散度的话,那 VAE 好像真的跟变分没多大关系了,因为 KL 散度的定义是:
KL(p(x)∣∣q(x))=∫p(x)lnp(x)q(x)dxKL(p(x)||q(x))=\int p(x)\ln \frac{p(x)}{q(x)}dxKL(p(x)∣∣q(x))=∫p(x)lnq(x)p(x)dx
如果是离散概率分布就要写成求和,我们要证明:已概率分布 p(x)(或固定q(x))的情况下,对于任意的概率分布 q(x)(或 p(x)),都有 KL(p(x)‖q(x))≥0,而且只有当p(x)=q(x)时才等于零。
KL散度的非负性证明
因为 KL(p(x)‖q(x))实际上是一个泛函,要对泛函求极值就要用到变分法,当然,这里的变分法只是普通微积分的平行推广,还没涉及到真正复杂的变分法。而 VAE 的变分下界,是直接基于 KL 散度就得到的。所以直接承认了 KL 散度的话,就没有变分的什么事了。
一句话,VAE 的名字中“变分”,是因为它的推导过程用到了 KL 散度及其性质。
相关文章:

VAE--part1
Variational Auto-Encoder, VAE__part1分布变换VAE慢谈VAE 初现分布标准化重参数技巧VAE的本质是什么?VAE的本质结构正态分布?变分在哪里参考博客仅做学习记录,侵删分布变换 VAE和GAN都是生成式模型,它们俩的目标基本一致&#x…...

备战四级!!!
目录 一、替换词 二、作文常见句型 (1)常见开头 (2)阐述观点 (3)结束语 (4)提出建议 (5)表示论证 (6)给出原因 (…...

sizeof与strlen练习
前言 本篇仅仅是为了更加了解sizeof操作符和strlen函数练习. 对于多条sizeof操作符和strlen函数出现,可能很容易造成头脑不清晰,做题时容易混乱. 目录前言一维数组字符数组情况1:情况2情况3二维数组练习之前请牢记下面这段话.这将是头脑清晰地关键. 提示: sizeof(数组名)&#…...
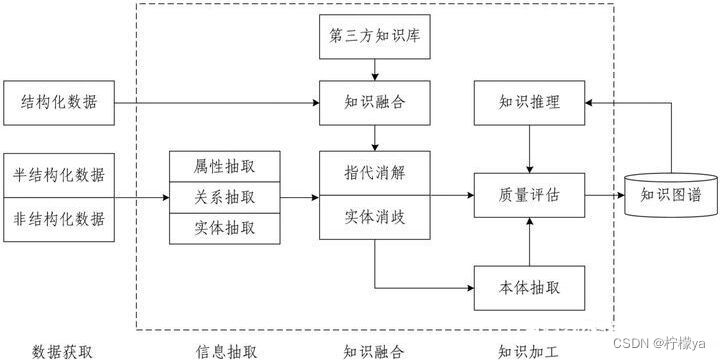
知识图谱的介绍
知识图谱的由来 谷歌在2012年提出了知识图谱的概念,当时目的在于优化搜索引擎的返回结构,为用户提供更精确的结果。 知识图谱的定义 为了理解知识图谱,我们首先要明白信息与知识的概念。首先,信息表示的是外部的客观事实&#…...

【Redis】Redis高级客户端Lettuce详解
文章目录前提Lettuce简介连接Redis定制的连接URI语法基本使用API同步API异步API反应式API发布和订阅事务和批量命令执行Lua脚本执行高可用和分片普通主从模式哨兵模式集群模式动态命令和自定义命令高阶特性配置客户端资源使用连接池几个常见的渐进式删除例子在SpringBoot中使用…...
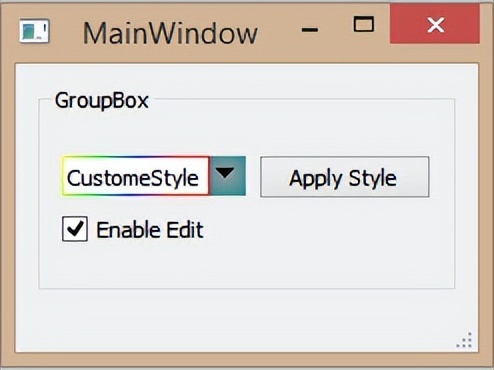
Qt——自定义界面之QStyle
1. Qt控件结构简介 首先我们要来讲讲GUI控件结构,这里以QComboBox为例: 一个完整的控件由一种或多种GUI元素构成: Complex Control Element。Primitive Element。Control Element。 1.1 Complex Control Element Complex control elements …...
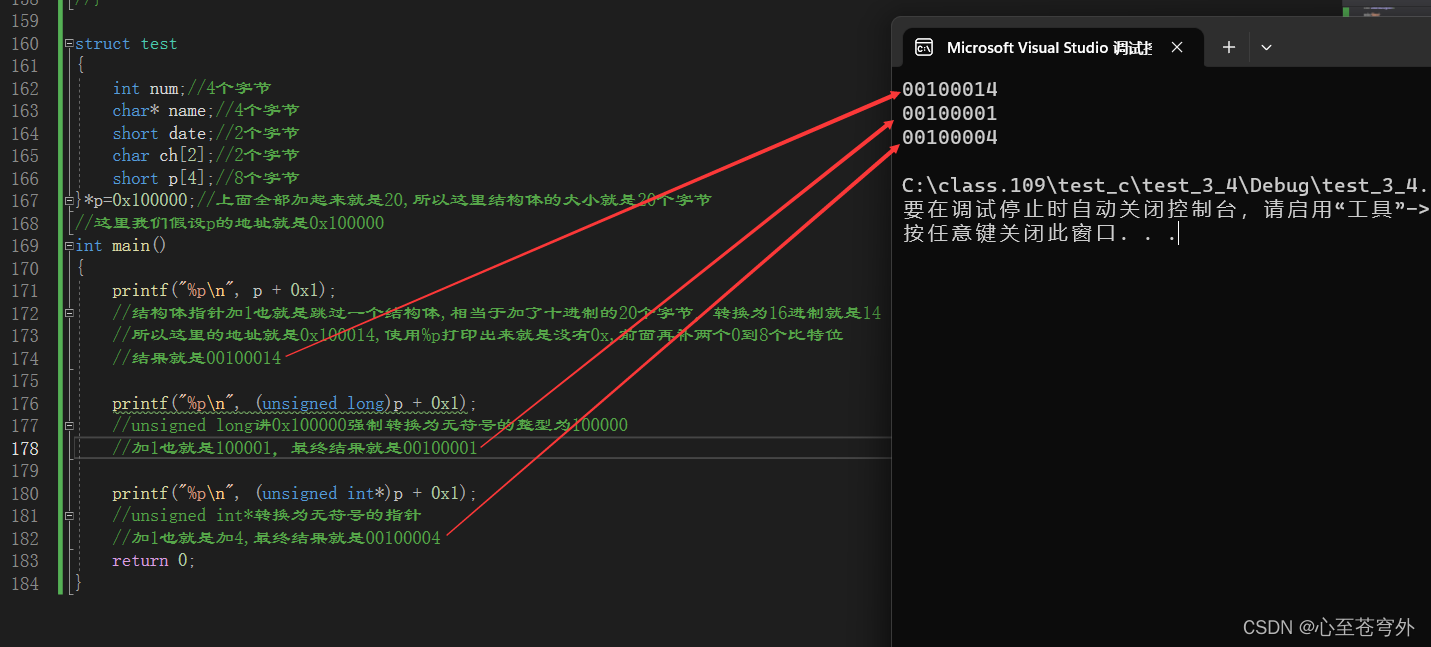
指针和数组面试题(逐题分析,完善你可能遗漏的知识)
人生不是一种享乐,而是一桩十分沉重的工作。 —— 列夫托尔斯泰 前言:之前我们就学习了数组和指针的知识。 数组:数组就是能够存放一组相同类型的元素,数组的大小取决于数组的元素个数和元素类型。 指针:…...

centos7搭建nfs挂载日志目录完整步骤
NFS服务器配置 1.安装NFS服务 首先使用yum安装nfs服务: yum -y install rpcbind nfs-utils 2.创建共享目录 在服务器上创建共享目录,并设置权限。 mkdir /data/share/ chmod 755 -R /data/share/ 3.配置NFS nfs的配置文件是 /etc/exports &…...
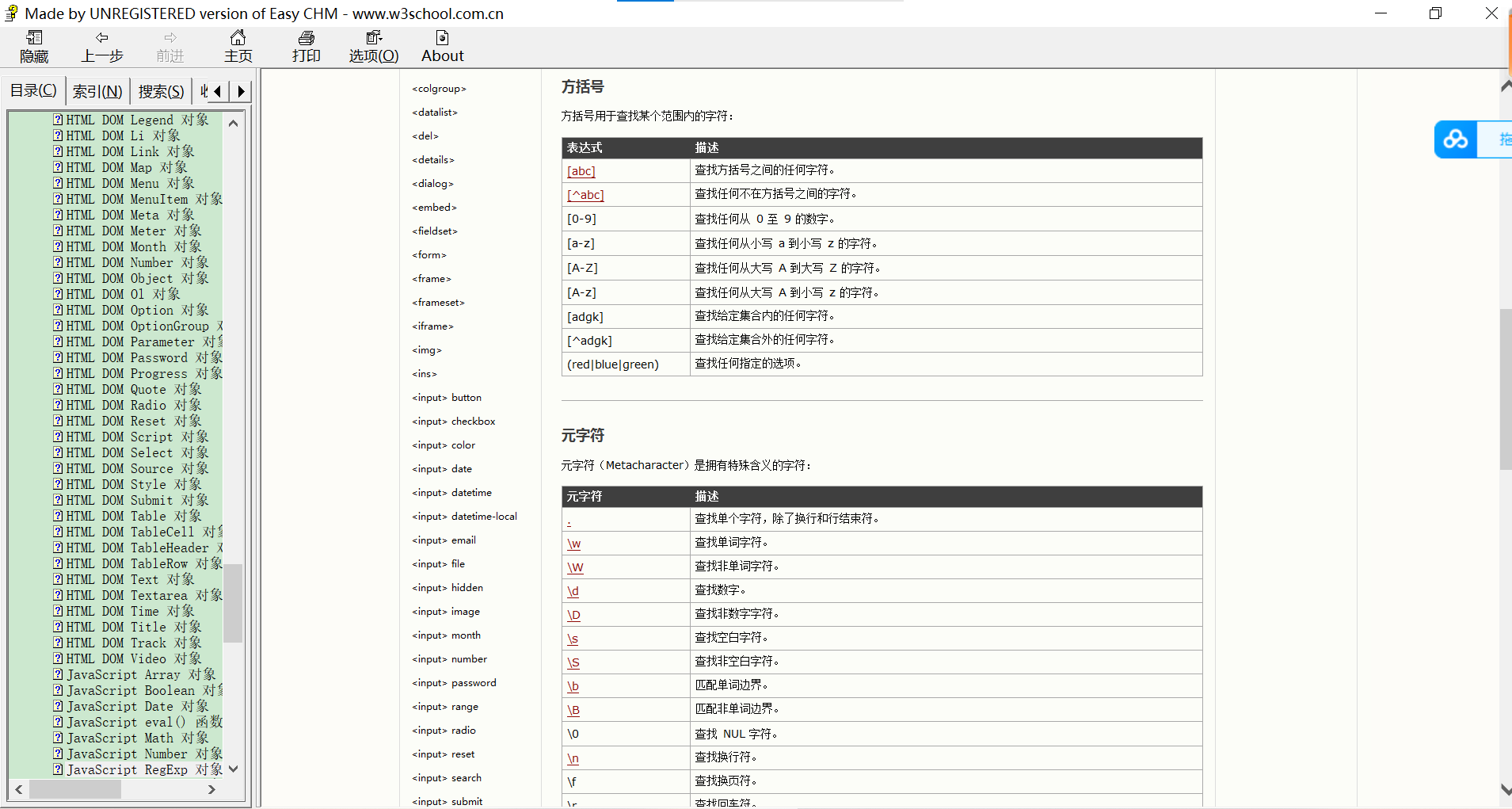
三、JavaScript
目录 一、JavaScript和html代码的结合方式 二、javascript和java的区别 1、变量 2、运算 3、数组(重点) 4、函数 5、重载 6、隐形参数arguments 7、js中的自定义对象 三、js中的事件 四、DOM模型 五、正则表达式 一、JavaScript和html代码的结合方…...

深圳大学计软《面向对象的程序设计》实验11 多继承
A. 在职研究生(多重继承) 题目描述 1、建立如下的类继承结构: 1)定义一个人员类CPeople,其属性(保护类型)有:姓名、性别、年龄; 2)从CPeople类派生出学生类CStudent,…...

并发变成实战-原子变量与非阻塞同步机制
文章目录1.锁的劣势2.硬件对并发的支持2.1 比较并交换2.2 非阻塞的计数器3.原子变量类3.1 原子变量是一种“更好的volatile”3.2 性能比较:锁与原子变量4.非阻塞算法4.1 非阻塞的栈4.2 非阻塞的链表4.3 ABA问题非阻塞算法设计和实现上要复杂的多,但在可伸…...
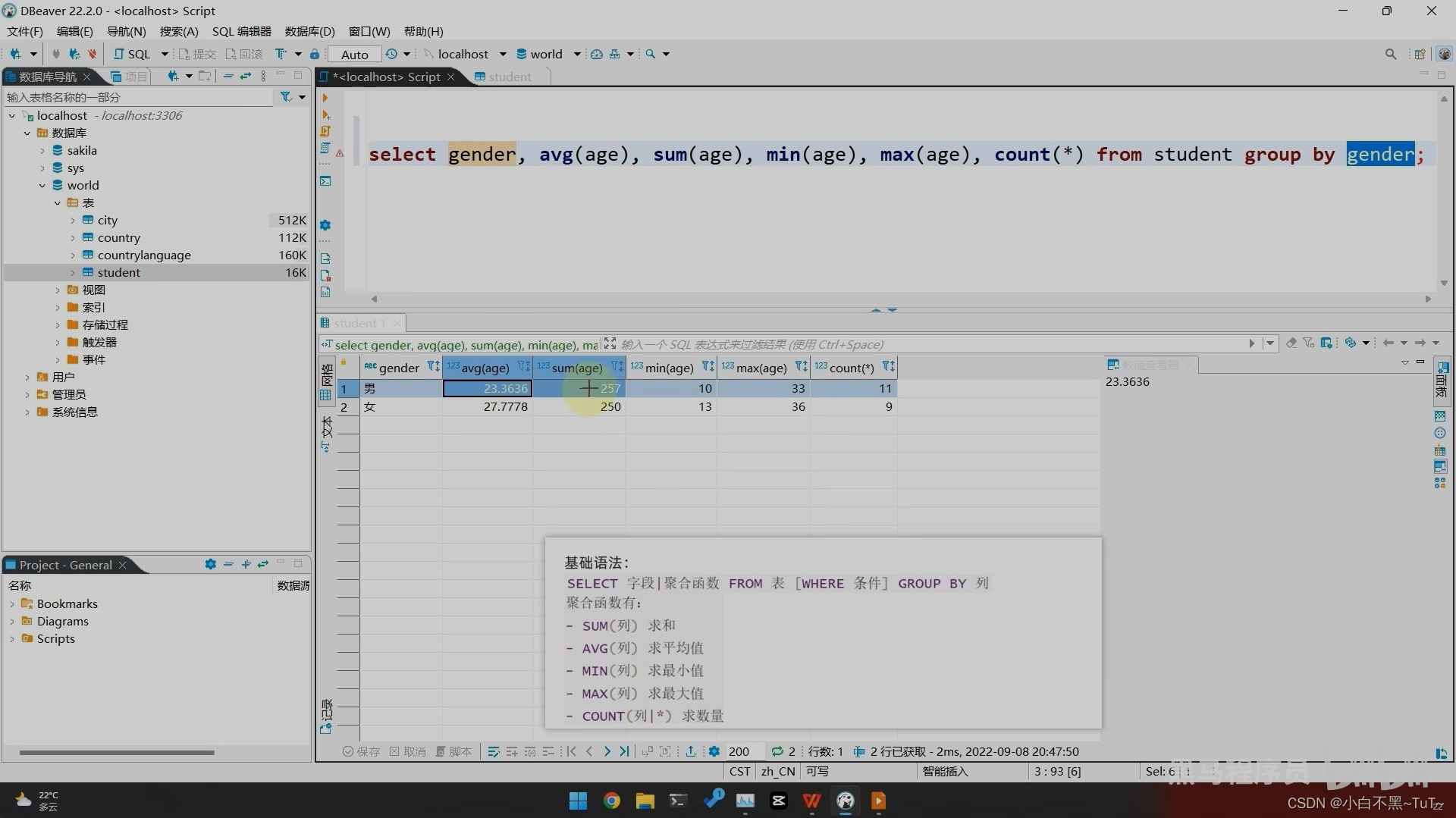
sql数据库常用操作指令
一、操作库-- 创建库create database db1;-- 创建库是否存在,不存在则创建create database if not exists db1;-- 查看所有数据库show databases;-- 查看某个数据库的定义信息 show create database db1; -- 修改数据库字符信息alter database db1 character set ut…...

4-1 定时任务的示例10个
文章目录前言基本命令与格式示例前言 Linux crontab 是用来定期执行程序的命令。当安装完成操作系统之后,默认都已经安装,并启动此任务调度命令。 crond 命令每分钟会定期检查是否有要执行的工作,如果有要执行的工作便会自动执行该工作。 基…...

外贸建站多少钱才能达到预期效果?
外贸建站多少钱才能达到预期效果?这是每个外贸企业都会问的问题。作为一个做外贸建站多年的人,我有一些个人的操盘感想。 首先,我认为外贸建站的投资是非常必要的。 因为在现代社会,网站已经成为外贸企业开展业务的必要工具之一…...

【Java学习笔记】5.Java 基本数据类型
Java 基本数据类型 变量就是申请内存来存储值。也就是说,当创建变量的时候,需要在内存中申请空间。 内存管理系统根据变量的类型为变量分配存储空间,分配的空间只能用来储存该类型数据。 因此,通过定义不同类型的变量…...

InnoDB 死锁和问题排查
文章目录死锁(dead lock)示例 1问题排查查看连接的线程查看相关的表查看最近一次的死锁信息查看服务器的锁信息查看正在使用的表如何尽可能地避免死锁死锁(dead lock) 两个及以上的事务各自持有对方需要的锁,导致双方…...
——六步法——鸢尾花数据集分类)
tensorflow07——使用tf.keras搭建神经网络(Sequential顺序神经网络)——六步法——鸢尾花数据集分类
使用tf.keras搭建顺序神经网络 六步法——鸢尾花数据集分类 01 导入相关包 02 导入数据集,打乱顺序 03 建立Sequential模型 04 编译——确定优化器,损失函数,评测指标(用哪一种准确率) 05 训练模型——把各项参入填入…...

关于Java连接Hive,Spark等服务的Kerberos工具类封装
关于Java连接Hive,Spark等服务的Kerberos工具类封装 idea连接服务器的hive等相关服务的kerberos认证注意事项 idea 本地配置,连接服务器;进行kerberos认证,连接hive、HDFS、Spark等服务注意事项: 本地idea连接Hadoo…...

大数据框架之Hadoop:MapReduce(五)Yarn资源调度器
Apache YARN (Yet Another Resource Negotiator) 是 hadoop 2.0 引入的集群资源管理系统。用户可以将各种服务框架部署在 YARN 上,由 YARN 进行统一地管理和资源分配。 简言之,Yarn是一个资源调度平台,负责为运算程序提供服务器运算资源&…...
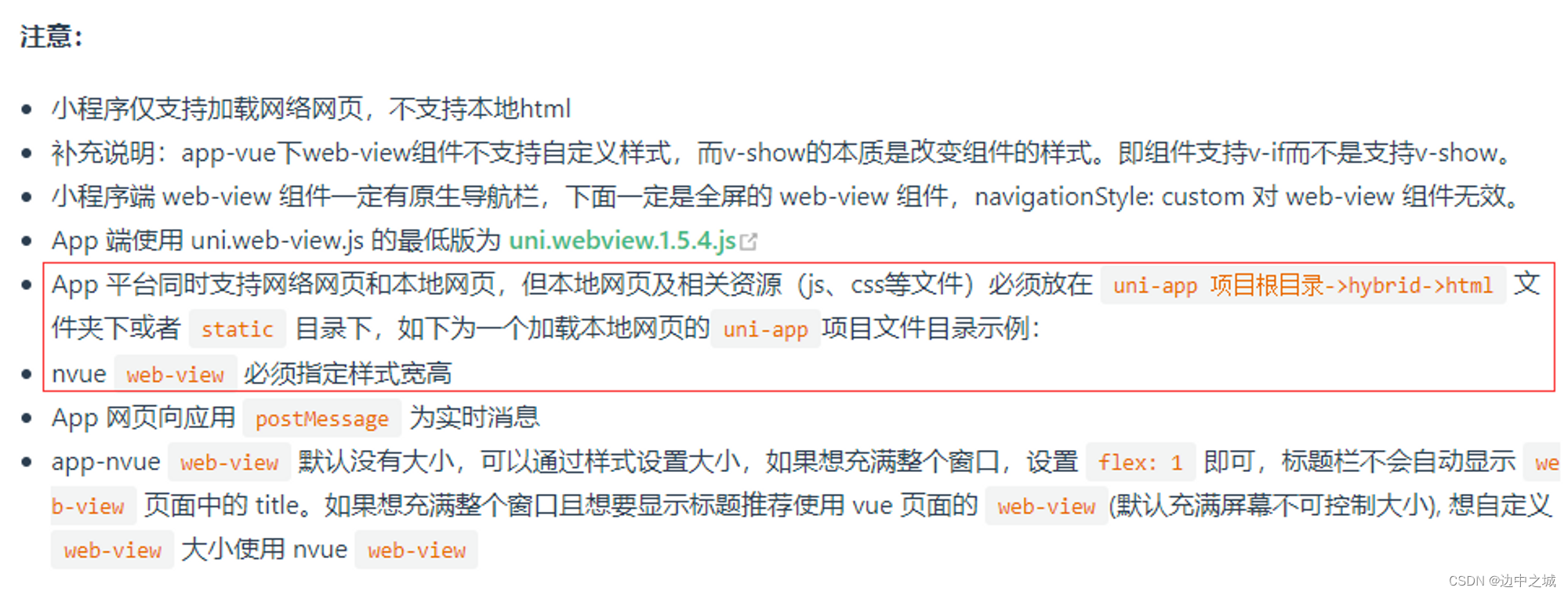
uniapp实现地图点聚合功能
前言 在工作中接到的一个任务,在app端实现如下功能: 地图点聚合地图页面支持tab切换(设备、劳务、人员)支持人员搜索显示分布 但是uniapp原有的map标签不支持点聚合功能(最新的版本支持了点聚合功能)&am…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...