2-SAT问题相关理论和算法
前言
SAT 问题简介
SAT是可满足性、适定性(Satisfiability)问题的简称。一般形式为k-适定性问题或k-可满足性问题,简称 k-SAT。
何为布尔可满足性问题?给定一条真值表达式,包含逻辑变量、逻辑与、逻辑或以及非运算符,如:
( a ∧ ¬ b ∧ ( ¬ ( c ∨ d ∨ ¬ a ) ∨ ( b ∧ ¬ d ) ) ) ∨ ( ¬ ( ¬ ( ¬ b ∨ a ) ∧ c ) ∧ d ) (a\wedge\neg b\wedge(\neg(c\vee d\vee\neg a)\vee(b\wedge\neg d)))\vee(\neg(\neg(\neg b\vee a)\wedge c)\wedge d) (a∧¬b∧(¬(c∨d∨¬a)∨(b∧¬d)))∨(¬(¬(¬b∨a)∧c)∧d)
是否存在一组对这些变量的赋值,使得整条式子最终的运算结果为 t r u e true true?若可以,那么这个性质被称为这条逻辑公式的可满足性(satisfiability),如何快速高效地判断任意指定逻辑公式的可满足性是理论计算机科学中的一个重要的问题,也是第一个被证明为NP-完全(NP-complete,NPC)的问题。
当 k > 2 k>2 k>2时,可满足性问题是NPC问题,因此我们一般只研究 k = 2 k=2 k=2的情况。
2-SAT算法
通常所说的2-SAT问题往往需要我们处理对于 n n n个布尔变量 { x n } ( x i ∈ { 0 , 1 } ) \{x_n\}\left(x_i\in\{0,1\}\right) {xn}(xi∈{0,1})的 m m m个限制。
其每个限制都形如一个 ∨ \vee ∨运算符连接的两个简单限制条件,简单限制条件为 x i = t r u e x_i=true xi=true(记作 x i x_i xi)或 x i = f a l s e x_i=false xi=false(记作 ¬ x i \neg x_i ¬xi),因此限制条件一共有四种:
- s k = x i ∨ x j s_k=x_i\vee x_j sk=xi∨xj
- s k = ¬ x i ∨ x j s_k=\neg x_i\vee x_j sk=¬xi∨xj
- s k = x i ∨ ¬ x j s_k=x_i\vee\neg x_j sk=xi∨¬xj
- s k = ¬ x i ∨ ¬ x j s_k=\neg x_i\vee \neg x_j sk=¬xi∨¬xj
我们需要满足: ⋀ m i = 1 s i = t r u e \underset{i=1}{\overset m{ \bigwedge }}s_i=true i=1⋀msi=true
也就是需要每一个 s k s_k sk都为真。
其处理方法为:
首先建图,对变量 x i x_i xi建立两个点 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1表示选 x i = 0 x_i=0 xi=0或 x i = 1 x_i=1 xi=1,然后在新图上对每个限制按照如下方式连边。
例如对于限制 s k s_k sk,我们讨论这条限制下 a , b ∈ { 0 , 1 } a,b\in\{0,1\} a,b∈{0,1}, x i = a x_i=a xi=a时是否一定有 x j = b x_j=b xj=b,如果一定有,就连有向边 x i , a → x j , b x_{i,a}\rightarrow x_{j,b} xi,a→xj,b。
同理我们讨论 x j = a x_j=a xj=a是否一定有 x i = b x_i=b xi=b,如果一定有,就连有向边 x j , a → x i , b x_{j,a}\rightarrow x_{i,b} xj,a→xi,b
感性理解这张图,如果 x i , a x_{i,a} xi,a可达 x j , b x_{j,b} xj,b,则说明 x i = a x_i=a xi=a可以推出 x j = b x_j=b xj=b,或者说 x i = a x_i=a xi=a蕴含了 x j = b x_j=b xj=b。
因此我们知道这个可满足性问题无解的充要条件为,存在 i i i使得 x i , 0 x_{i,0} xi,0和 x i , 1 x_{i,1} xi,1处于同一个强连通分量内,这意味着 x i = 0 x_i=0 xi=0推出 x i = 1 x_i=1 xi=1,同时 x i = 1 x_i=1 xi=1推出 x i = 0 x_i=0 xi=0,因此无解。
因此我们可以使用Tarjan算法求强连通分量来判断2-SAT问题是否有解,事实上我们还可以输出一组可行解。
具体方法如下,首先对我们建图的图求强连通分量缩点,得到一张DAG,然后对DAG进行拓扑排序,则 x i x_i xi对应的两个节点中,对应的强连通分量拓扑序较为靠后的节点对应的权值,是 x i x_i xi取得的权值。
其原理是,如果 x i = a x_i=a xi=a会推出 x i = b x_i=b xi=b,那么就不能选 x i = a x_i=a xi=a,此时只能选 x i = b x_i=b xi=b。
这样我们就用Tarjan算法取得了可满足性问题的 O ( n + m ) O(n+m) O(n+m)做法。
具体的连边方式
首先,所有限制都可以转化为 x i = a ⇒ x j = b x_i=a\Rightarrow x_j=b xi=a⇒xj=b的形式进行连边,这里记录一些经典的连边方式,这样就不需要每次做转化了。
- x i = a ⇒ x j = b x_i=a\Rightarrow x_j=b xi=a⇒xj=b
- x i , a → x j , b x_{i,a}\rightarrow x_{j,b} xi,a→xj,b
- x j , ¬ b → x i , ¬ a x_{j,\neg b}\rightarrow x_{i,\neg a} xj,¬b→xi,¬a
- a ∨ b a\vee b a∨b
- a 0 → b 1 a_0\rightarrow b_1 a0→b1
- b 0 → a 1 b_0\rightarrow a_1 b0→a1
- ¬ a ∨ b \neg a\vee b ¬a∨b
- a 1 → b 1 a_1\rightarrow b_1 a1→b1
- b 0 → a 0 b_0\rightarrow a_0 b0→a0
- ¬ a ∨ ¬ b \neg a\vee\neg b ¬a∨¬b
- a 1 → b 0 a_1\rightarrow b_0 a1→b0
- b 1 → a 0 b_1\rightarrow a_0 b1→a0
- a = t r u e a=true a=true
- 转化为 a = 0 ⇒ a = 1 a=0\Rightarrow a=1 a=0⇒a=1
- a 0 → a 1 a_0\rightarrow a_1 a0→a1
- a = f a l s e a=false a=false
- 转化为 a = 1 ⇒ a = 0 a=1\Rightarrow a=0 a=1⇒a=0
- a 1 → a 0 a_1\rightarrow a_0 a1→a0
- a = b a=b a=b
- 转化为 a = 1 ⇒ b = 1 a=1\Rightarrow b=1 a=1⇒b=1,且 a = 0 ⇒ b = 0 a=0\Rightarrow b=0 a=0⇒b=0
- a ≠ b a\not=b a=b( a ⊗ b a\otimes b a⊗b)
- 转化为 a = 0 ⇒ b = 1 a=0\Rightarrow b=1 a=0⇒b=1,且 a = 1 ⇒ b = 0 a=1\Rightarrow b=0 a=1⇒b=0
- x 1 , x 2 , x 3 , . . . x_1,x_2,x_3,... x1,x2,x3,...至多一个为真
- 转化为:
- x 1 = 1 ⇒ x 2 = 0 x_1=1\Rightarrow x_2=0 x1=1⇒x2=0,且 x 1 = 1 ⇒ x 3 = 0 x_1=1\Rightarrow x_3=0 x1=1⇒x3=0,…
- 且 x 2 = 1 ⇒ x 1 = 0 x_2=1\Rightarrow x_1=0 x2=1⇒x1=0,且 x 2 = 1 ⇒ x 3 = 0 x_2=1\Rightarrow x_3=0 x2=1⇒x3=0,…
- 且 x 3 = 1 ⇒ x 1 = 0 x_3=1\Rightarrow x_1=0 x3=1⇒x1=0,且 x 3 = 1 ⇒ x 2 = 0 x_3=1\Rightarrow x_2=0 x3=1⇒x2=0,…
- …
- 注意这样连出来的边数是 O ( m 2 ) O(m^2) O(m2)级别的
- 转化为:
- x 1 , x 2 , x 3 , . . . x_1,x_2,x_3,... x1,x2,x3,...至多 k > 1 k>1 k>1个为真
- 2-sat一般不能做
- x 1 , x 2 , x 3 , . . . x_1,x_2,x_3,... x1,x2,x3,...至少 k ≥ 1 k\geq 1 k≥1个为真
- 2-sat一般不能做
- x 1 , x 2 , x 3 , . . . x_1,x_2,x_3,... x1,x2,x3,...恰好 k ≥ 1 k\geq 1 k≥1个为真
- 2-sat一般不能做
其中一些限制条件也可以在连边的时候判掉。
2-SAT原理
我们现在有 n n n个布尔变量,称为 { x n } ( x i ∈ { 0 , 1 } ) \{x_n\}\left(x_i\in \{0,1\}\right) {xn}(xi∈{0,1}),现在给出 m m m条限制,每一条限制都形如:
当 x i = a x_i=a xi=a时,有 x j = b x_j=b xj=b( a , b ∈ { 0 , 1 } a,b\in\{0,1\} a,b∈{0,1})
即: x i = a ⇒ x j = b x_i=a\Rightarrow x_j=b xi=a⇒xj=b
接下来说一下如何求解这个问题。
图的建立
点的意义
我们使用图论方法对这个问题进行求解,按照经典套路,我们需要在图上定义一个集合,然后把原问题的意义在集合内体现出来。
具体来说,我们有一个集合 S S S,同时在图上有 2 n 2n 2n个点,其中每个比尔变量 x i x_i xi对应两个点,一个叫做 x i , 0 x_{i,0} xi,0,另一个叫做 x i , 1 x_{i,1} xi,1。
我们规定 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1当中只能恰好有一个属于集合 S S S,如果 x i , 0 ∈ S x_{i,0}\in S xi,0∈S,则 x i = 0 x_i=0 xi=0;如果 x i , 1 ∈ S x_{i,1}\in S xi,1∈S,则 x i = 1 x_i=1 xi=1。
我们知道根据限制能够推出一些关系,例如如果 x i , a ∈ S x_{i,a}\in S xi,a∈S,那么一定有 x j , b ∈ S x_{j,b}\in S xj,b∈S,我们希望用边表示这一种关系,因此我们规定对于任意元素 u ∈ S u\in S u∈S, u u u在图上可达的所有点 v v v均属于 S S S。
边的意义
刚才已经定义了图中的点,以及集合 S S S。现在具体说一下图中的边是如何连接的:
对于限制: x i = a ⇒ x j = b x_i=a\Rightarrow x_j=b xi=a⇒xj=b
我们考虑一个一个向着集合 S S S内添加元素的过程,我们必然是找到一个点 u u u加入集合,然后将 u u u的所有后继加入 S S S,然后把这些后继的所有后继加入 S S S…
由于我们知道 x i = a x_i=a xi=a时, x j = b x_j=b xj=b,因此对于这个限制,我们在图上连边 x i , a → x j , b x_{i,a}\rightarrow x_{j,b} xi,a→xj,b,这样就似乎可以表示这个限制了。
(注意连边方式到这里还不完全正确)
此时我们会得到一个暴力算法:
- 枚举一个未被确定的变量 x i x_i xi
- 先选择 x i , 0 x_{i,0} xi,0,然后检查 x i , 0 x_{i,0} xi,0可达的所有点,我们将会选中他们。
- 如果发生冲突(即存在 x j , 0 , x j , 1 ∈ S x_{j,0},x_{j,1}\in S xj,0,xj,1∈S),那么就说明 x i ≠ 0 x_i\not=0 xi=0,回溯。
- 如果 x i , 0 x_{i,0} xi,0不能选,那么就选择 x i , 1 x_{i,1} xi,1,然后检查 x i , 1 x_{i,1} xi,1的可达点,检查是否有冲突,如果没有就选上它们,否则就说明无解。
但是我们会发现这个算法是会错的,举例来说,对于以下两个限制:
- y = 0 ⇒ x = 1 y=0\Rightarrow x=1 y=0⇒x=1
- y = 1 ⇒ x = 1 y=1\Rightarrow x=1 y=1⇒x=1
我们会连出这张图:
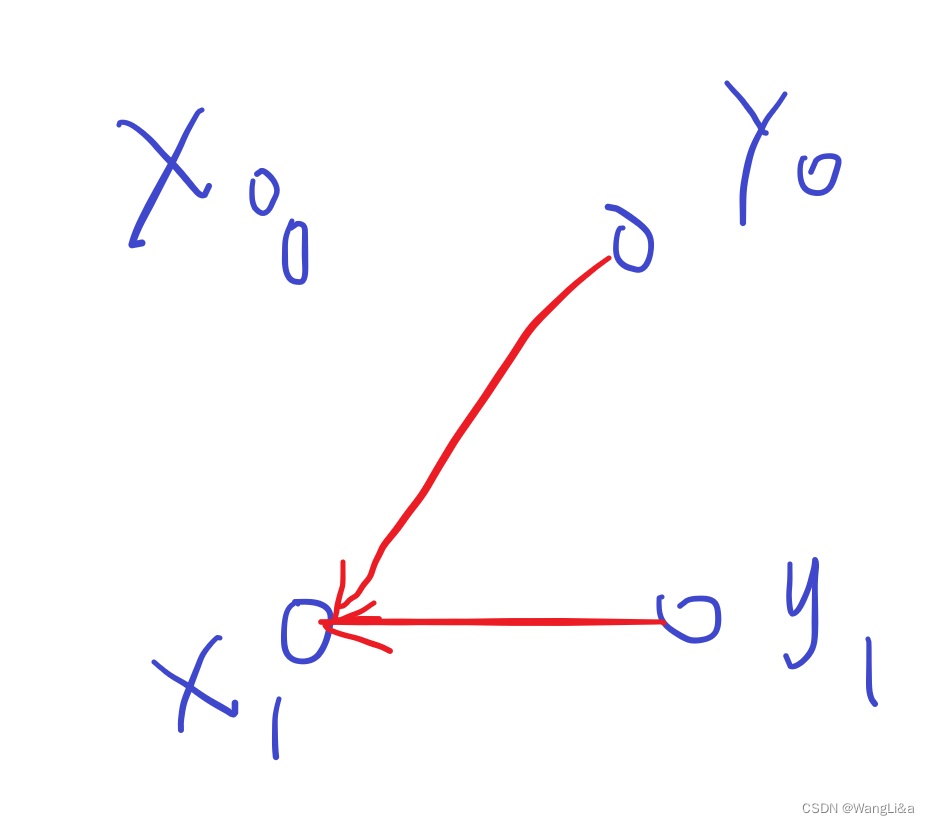
但是如果我们一开始选择 x 0 x_0 x0,后来就会发现无论选择 y 0 y_0 y0还是 y 1 y_1 y1都会有矛盾,此时就输出无解,显然是不对的。
这样会出错是因为,对于这样的一条限制 y = 0 ⇒ x = 1 y=0\Rightarrow x=1 y=0⇒x=1来说,选择 x x x的值是会对 y y y的值产生影响的,具体来说,如果 x = 0 x=0 x=0,这就说明 y ≠ 0 y\not=0 y=0,即 y = 1 y=1 y=1。
换句话说,命题 y = 0 ⇒ x = 1 y=0\Rightarrow x=1 y=0⇒x=1的逆否命题 x ≠ 1 ⇒ y ≠ 0 x\not=1\Rightarrow y\not =0 x=1⇒y=0,即 x = 0 ⇒ y = 1 x=0\Rightarrow y=1 x=0⇒y=1,具有和原命题一致的真假性,因此选择 x x x的值可能会对 y y y造成影响,因此我们需要进一步讨论 x = a ⇒ y = b x=a\Rightarrow y=b x=a⇒y=b说明了 x , y x,y x,y之间的那些关系:
- 当我们选择了 x a x_a xa时,必然有 y b y_b yb
- 当我们选择了 x ¬ a x_{\neg a} x¬a时,这条限制不提供任何约束,即有可能选择 y b y_b yb或 y ¬ b y_{\neg b} y¬b
- 当我们选择了 y b y_b yb时,这条限制不提供任何约束,即有可能选择 x a x_a xa或 x ¬ a x_{\neg a} x¬a
- 当我们选择了 y ¬ b y_{\neg b} y¬b时,必然有 x ¬ a x_{\neg a} x¬a
因此事实上对于限制 x i = a ⇒ x j = b x_i=a\Rightarrow x_{j}=b xi=a⇒xj=b来说,我们应该连接两条边:
- x i , a → x j , b x_{i,a}\rightarrow x_{j,b} xi,a→xj,b
- x j , ¬ b → x i , ¬ a x_{j,\neg b}\rightarrow x_{i,\neg a} xj,¬b→xi,¬a
此时我们再进行刚才的暴力算法,我们就获得了时间复杂度为 O ( n ⋅ m ) O(n\cdot m) O(n⋅m)的2-sat问题的dfs做法。值得一提的是,这种做法还能同时让我们获得2-sat问题字典序最小的解。
接下来简要对暴力做法的正确性进行说明:
首先我们证明解的充分性,即我们求出的解确实是原问题的一组解:
首先我们知道,对于一个限制 x i = a ⇒ x j = b x_{i}=a\Rightarrow x_{j}=b xi=a⇒xj=b,这个限制被违反当且仅当 x i , a , x j , ¬ b ∈ S x_{i,a},x_{j,\neg b}\in S xi,a,xj,¬b∈S。
如果说在算法过程中 x i , a x_{i,a} xi,a比 x j , ¬ b x_{j,\neg b} xj,¬b先选的话,发生这种情况一定不可能,因为我们选择 x i , a x_{i,a} xi,a时根据连边,一定选择了 x j , b x_{j,b} xj,b,因此后来无法选择 x j , ¬ b x_{j,\neg b} xj,¬b了,矛盾。
如果 x i , a x_{i,a} xi,a比 x j , ¬ b x_{j,\neg b} xj,¬b后选的话,这种情况还是不可能,因为根据连边的方式,如果我们选择了 x j , ¬ b x_{j,\neg b} xj,¬b,我们一定选择了 x i , ¬ a x_{i,\neg a} xi,¬a,不可能再选择 x i , a x_{i,a} xi,a,因此仍然矛盾。
因此我们就证明,我们构造出的一组解满足所有限制条件,因此是一组合法解。
接下来我们证明解的必要性,即有解的时候,我们一定能够构造出一组解。
只需证明逆否命题,即如果我们构造不出一组解,此时这个问题无解。
我们考虑求解过程在决定变量 x i x_i xi的取值时报告了无解。
此时必然是因为发生了矛盾,首先讨论选取 x i , 0 x_{i,0} xi,0时候的情况,矛盾即存在元素 x j , 0 , x j , 1 ∈ S x_{j,0},x_{j,1}\in S xj,0,xj,1∈S。
此时有两种情况,第一种情况是 x j , 0 , x j , 1 x_{j,0},x_{j,1} xj,0,xj,1都是在 x i , 0 x_{i,0} xi,0加入集合 S S S后加入集合的,此时显然选择 x i , 0 x_{i,0} xi,0会同时推出 x j = 0 x_j=0 xj=0和 x j = 1 x_j=1 xj=1,因此 x i ≠ 0 x_i\not=0 xi=0。
第二种情况是, x j , a x_{j,a} xj,a是在 x i , 0 x_{i,0} xi,0加入集合 S S S前加入集合的,而 x j , ¬ a x_{j,\neg a} xj,¬a是因为加入 x i , 0 x_{i,0} xi,0而加入集合 S S S的(换句话说存在路径使得 x i , 0 ⇝ x j , ¬ a x_{i,0}\rightsquigarrow x_{j,\neg a} xi,0⇝xj,¬a),这种情况不存在,这是因为,如果存在路径使得 x i , 0 ⇝ x j , ¬ a x_{i,0}\rightsquigarrow x_{j,\neg a} xi,0⇝xj,¬a,由于接下来说到的性质2,我们必然知道存在一条路径使得 x j , a ⇝ x i , 1 x_{j,a}\rightsquigarrow x_{i,1} xj,a⇝xi,1,因此当 x j , a ∈ S x_{j,a}\in S xj,a∈S后, x i , 1 ∈ S x_{i,1}\in S xi,1∈S,这与 x i x_i xi取值未确定矛盾,因此第二种情况不存在。
不可能存在一种情况使得 x j , 0 , x j , 1 x_{j,0},x_{j,1} xj,0,xj,1在加入 x i , 0 x_{i,0} xi,0前都在集合 S S S内,因为这违反 S S S的定义。
同理我们知道,如果在选择 x i , 1 x_{i,1} xi,1的时候发生矛盾,只可能是因为 x i ≠ 1 x_i\not=1 xi=1。此时我们就得知了 x i ≠ 0 x_i\not=0 xi=0且 x i ≠ 1 x_i\not=1 xi=1,因此得到这个可满足性问题无解。
QED.
线性算法
接下来我们说一下这个问题的线性算法,线性算法是这样的:
- 对建出来的图缩强连通分量
- 这样会得到一张DAG
- 如果存在点 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1在一个强连通分量内,则说明无解。
- 否则有解,对DAG拓扑排序, x i x_i xi的取值是它对应的两个点 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1对应的强连通分量中拓扑序较靠后的那个点的取值。
证明
接下来我们证明一下线性算法的正确性。
性质1
边的对称性:
对于任意一条有向边, ( x i , a , x j , b ) (x_{i,a},x_{j,b}) (xi,a,xj,b),都存在有向边 ( x j , ¬ b , x i , ¬ a ) (x_{j,\neg b},x_{i,\neg a}) (xj,¬b,xi,¬a),我们称为其对称边。
证明:
回忆建图的方式,这条性质是显然成立的。
性质2
路径的对称性:
对于任意一条从 x i , a x_{i,a} xi,a到 x j , b x_{j,b} xj,b的路径,必然存在对应的一条路径从 x j , ¬ b x_{j,\neg b} xj,¬b到 x i , ¬ a x_{i,\neg a} xi,¬a。
证明:
我们找到从 x i , a x_{i,a} xi,a到 x j , b x_{j,b} xj,b的路径上的每一条边的对称边,显然它们拼成一条从 x j ¬ b x_{j\neg b} xj¬b到 x i , ¬ a x_{i,\neg a} xi,¬a的路径。
算法1
我们可以据此提出一个求解2-sat问题的算法:
- 对建出来的图缩强连通分量
- 这样会得到一张DAG
- 如果存在点 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1在一个强连通分量内,则说明无解。
- 否则有解,我们通过如下过程构造解:
- 找到一个没有确定的 x i x_i xi
- 由于 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1不强连通,因此不可能存在二者相互可达。
- 如果有 x i , 0 ⇝ x i , 1 x_{i,0}\rightsquigarrow x_{i,1} xi,0⇝xi,1,那就令 x i , 1 ∈ S x_{i,1}\in S xi,1∈S。否则说明一定有 x i , 1 ⇝ x i , 0 x_{i,1}\rightsquigarrow x_{i,0} xi,1⇝xi,0,或者 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1互相不可达,此时令 x i , 0 ∈ S x_{i,0}\in S xi,0∈S。
- 如果此时我们有 x i , a ∈ S x_{i,a}\in S xi,a∈S,那就说明有 x i , ¬ a ∉ S x_{i,\neg a}\notin S xi,¬a∈/S。同时说明 x i , a x_{i,a} xi,a的所有后继都属于 S S S,把它们加入 S S S。
- 同时说明 x i , ¬ a x_{i,\neg a} xi,¬a的所有前驱都不属于 S S S。
- 直到所有的变量取值都确定,此时我们得到了一组可行解。
定理1
缩点后得到的DAG,满足没有任何一个 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1强连通,是原问题有解的必要条件。
证明其逆否命题:
如果存在 x i , 0 , x i , 1 x_{i,0},x_{i,1} xi,0,xi,1强连通,那么我们沿着 x i , 0 ⇝ x i , 1 ⇝ x i , 0 x_{i,0}\rightsquigarrow x_{i,1}\rightsquigarrow x_{i,0} xi,0⇝xi,1⇝xi,0的回路走,上面的边对应的限制条件就说明,当 x i = 0 x_{i}=0 xi=0时 x i = 1 x_i=1 xi=1,并且当 x i = 1 x_i=1 xi=1时 x i = 0 x_i=0 xi=0,此时显然无解。
QED.
定理2
按照上述算法1流程构造出的解,是原问题的一组解。
证明:
如果这组解不是原问题的一组解,那么一定存在至少一个限制被违背了,设这个限制是 x i = a ⇒ x j = b x_i=a\Rightarrow x_j=b xi=a⇒xj=b,这个限制被违反必须有 x i = a x_i=a xi=a且 x j = ¬ b x_j=\neg b xj=¬b。
假如说 x i , a x_{i,a} xi,a比 x j , ¬ b x_{j,\neg b} xj,¬b后晚加入集合,当我们加入 x j , ¬ b x_{j,\neg b} xj,¬b时,由于这条限制对应连出的边, x i , ¬ a x_{i,\neg a} xi,¬a一定也会被加入集合,因此 x i , a x_{i,a} xi,a不可能加入集合,矛盾。
否则说明 x i , a x_{i,a} xi,a比 x j , ¬ b x_{j,\neg b} xj,¬b先加入集合,但是这也不可能,因为当我们加入 x i , a x_{i,a} xi,a时,由于这条限制对应连出的边, x j , b x_{j,b} xj,b也一定加入集合,因此 x j , b x_{j,b} xj,b不可能加入集合,矛盾。
QED.
定理3
根据定理1,定理2,我们证明了:
算法1能够求出一组解,是原问题有解的充要条件。它求出的解,是原问题的一组解。
定理4
容易发现Tarjan算法+拓扑排序求解2-sat问题的过程事实上在模拟算法1,因此其的正确性也有保证。
后记
于是皆大欢喜。
相关文章:

2-SAT问题相关理论和算法
前言 SAT 问题简介 SAT是可满足性、适定性(Satisfiability)问题的简称。一般形式为k-适定性问题或k-可满足性问题,简称 k-SAT。 何为布尔可满足性问题?给定一条真值表达式,包含逻辑变量、逻辑与、逻辑或以及非运算符,如&#x…...
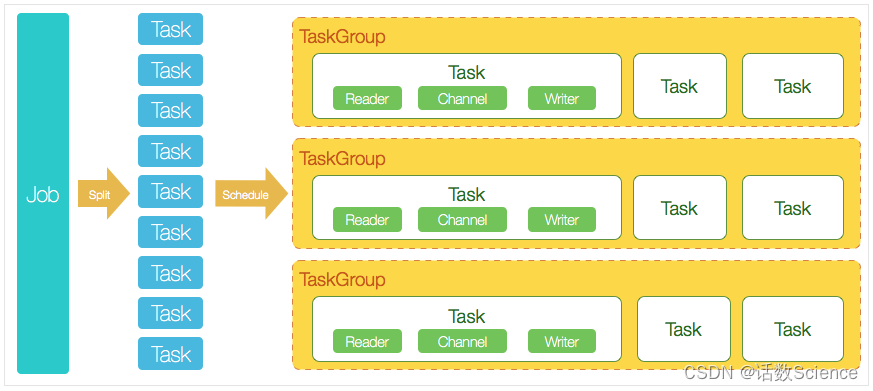
【大数据精讲】全量同步与CDC增量同步方案对比
目录 背景 名词解释 问题与挑战 FlinkCDC DataX 工作原理 调度流程 五、DataX 3.0六大核心优势 性能优化 背景 名词解释 CDC CDC又称变更数据捕获(Change Data Capture),开启cdc的源表在插入INSERT、更新UPDATE和删除DELETE活动时…...

自定义通用返回对象
目的:给返回对象补充一些信息,告诉前端这个请求在业务层面上是成功还是失败,以及具体的描述信息。 我们需要自定义错误码(因为前端的HTTP状态码默认的值比较少)和正常错误返回类。 ErrorCode : package …...

从0开始python学习-51.pytest之接口加密封装
目录 MD5加密 base64加密 rsa加密 MD5加密 1. 封装加密方法 def md5_encode(self,data):data str(data).encode("utf-8")md5_data hashlib.md5(data).hexdigest()return md5_data 2. 写入需要使用加密的接口yaml用例 -request:method: posturl: http://192.168.…...

c++的命名空间
命名空间 一.c的关键字二.命名空间2.1 命名空间定义2.1 命名空间的使用2.1.1加命名空间名称及作用域限定符2.1.2使用using将命名空间中某个成员引入 三.标准命名空间std 一.c的关键字 c中一共有63个关键字 关键字11111asmdoifreturntrycontinueautodoubleinlineshorttypedeff…...
)
阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
【题目描述】 输入一个高精度的正整数n�,去掉其中任意s�个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的n�和s�,寻找一种方案使得剩下的数字组成的新数最小。 输出新的正整数。࿰…...

大数据平台红蓝对抗 - 磨利刃,淬精兵!
背景 目前大促备战常见备战工作:专项压测(全链路压测、内部压测)、灾备演练、降级演练、限流、巡检(监控、应用健康度)、混沌演练(红蓝对抗),如下图所示。随着平台业务越来越复杂&a…...
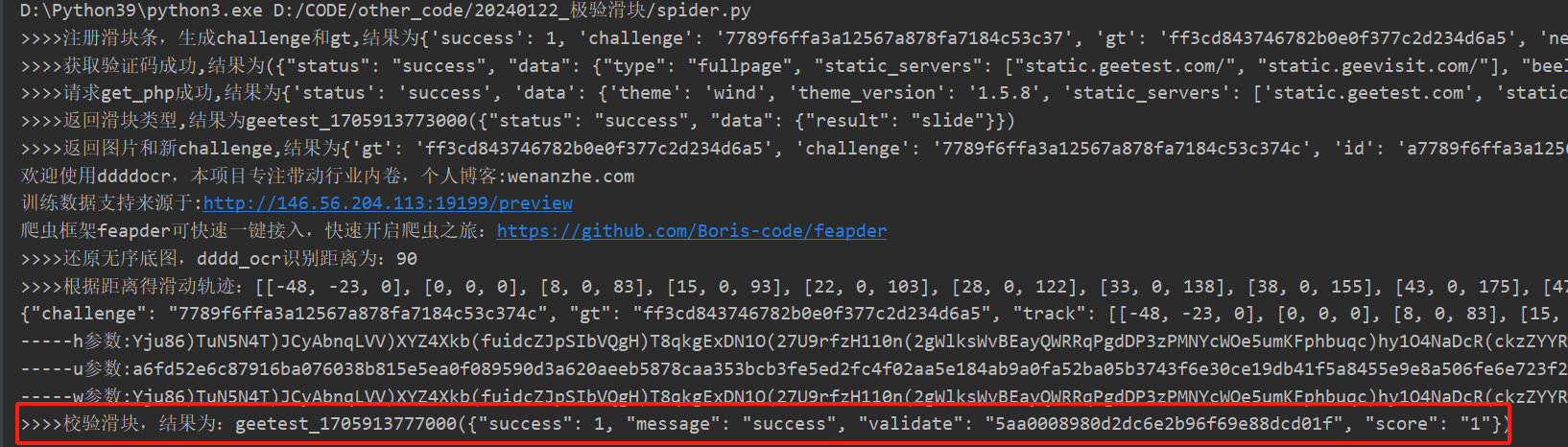
【2024-01-22】某极验3流程分析-滑块验证码
声明:该专栏涉及的所有案例均为学习使用,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!如有侵权,请私信联系本人删帖! 文章目录 一、前言二、抓包流程分析1.刷新页面2.点击按钮进行验证…...

Laya2.13.3接入FGUI
下载与复制文件与Laya1.x类似,可以看我上一篇: Laya1.8.4接入FariyGui,以及其中踩的坑-CSDN博客 不同的是: 两个库文件需要在index.js中引入 新建一个脚本将fgui中搭建好的UI包引入: export default class GameApp…...
短视频账号矩阵系统+无人直播系统源码技术开发
短视频账号矩阵系统无人直播系统源码技术开发涉及到多个领域,包括但不限于前端开发、后端开发、数据库设计、网络通信等。 以下是一些基本技术的步骤和注意事项: 1.技术需求分析设计:首先,需要明确开发短视频账号矩阵系统和无人直…...
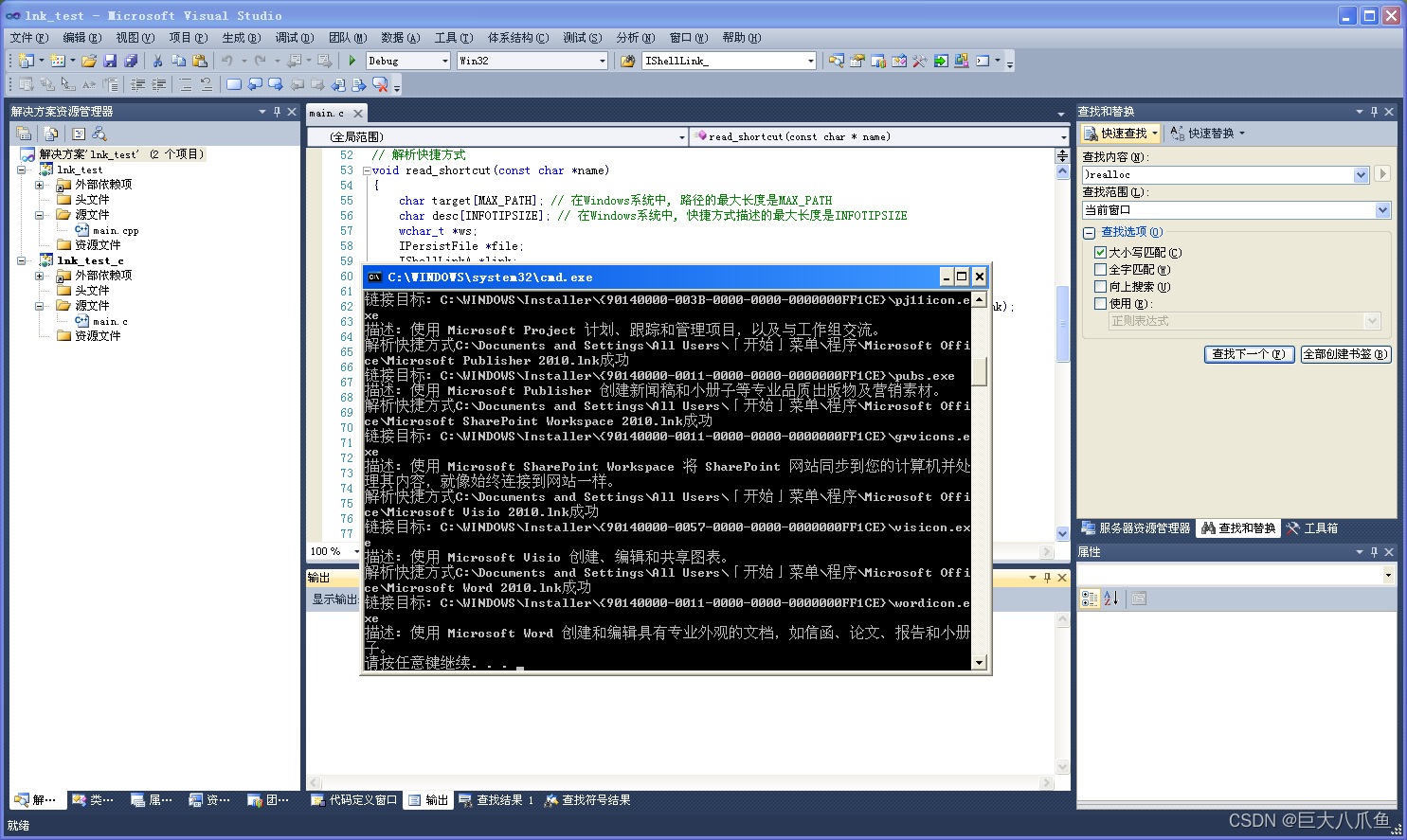
C语言或C++通过IShellLinkA创建或解析lnk快捷方式(使用char字符数组)
本例程用到的COM接口有IShellLinkA和IPersistFile。 请注意因为函数参数的类型不为BSTR,所以这两个接口可直接传char *或wchar_t *字符串,不需要提前转化为BSTR类型。 C语言的写法: /* 这个程序只能在C编译器下编译成功, 请确保源文件的扩展…...

Spring源码学习-Spring流程概述(一)
Spring启动的流程 public class Test {public static void main(String[] args) {ClassPathXmlApplicationContext context new ClassPathXmlApplicationContext("applicationContext.xml");Student bean context.getBean(Student.class);context.close();} }调用…...
Figma怎么设置中文,Figma有中文版吗?
不是很多人不想用 Figma,真是因为纯英文界面而头疼。这就是为什么有人会到处搜索 Figma 如何设置中文这样的问题。 然后我们直接快刀斩乱麻,Figma 没有中文版,但是我们还有其他的方法:例如, Figma 添加一个插件来解决…...
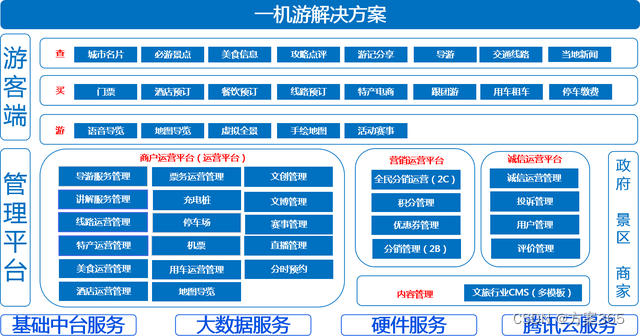
智慧文旅一机游:科技与文化的完美结合,引领智慧文旅新潮流,智慧旅游未来已来
一、科技与文化的完美结合:智慧文旅一机游的核心理念 智慧文旅一机游,是科技与文化相融合的产物,它不仅代表着旅游行业的创新与发展,更是一种文化与科技完美结合的生活方式。一机游的核心理念在于通过先进的科技手段,提…...

多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测
多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测 目录 多维时序 | Matlab实现CNN-LSTM-Mutilhead-Attention卷积长短期记忆神经网络融合多头注意力机制多变量时间序列预测效果一览基本介绍程序设计参考资料 效果…...
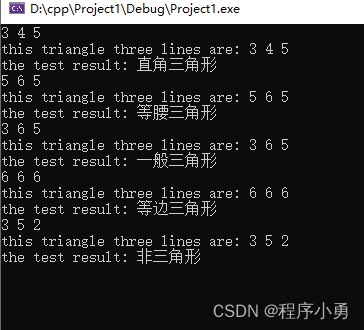
软件工程实验报告(完整)
博主介绍:✌全网粉丝喜爱、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦! 🍅附上相关C语言版源码讲解🍅 ὄ…...

Java零基础学习20:集合的练习
编写博客目的:本系列博客均根据B站黑马程序员系列视频学习和编写目的在于记录自己的学习点滴,方便后续回忆和查找相关知识点,不足之处恳请各位有缘的朋友指正。 一、查找id对应的集合索引 package www.itheima;import java.util.ArrayList;…...
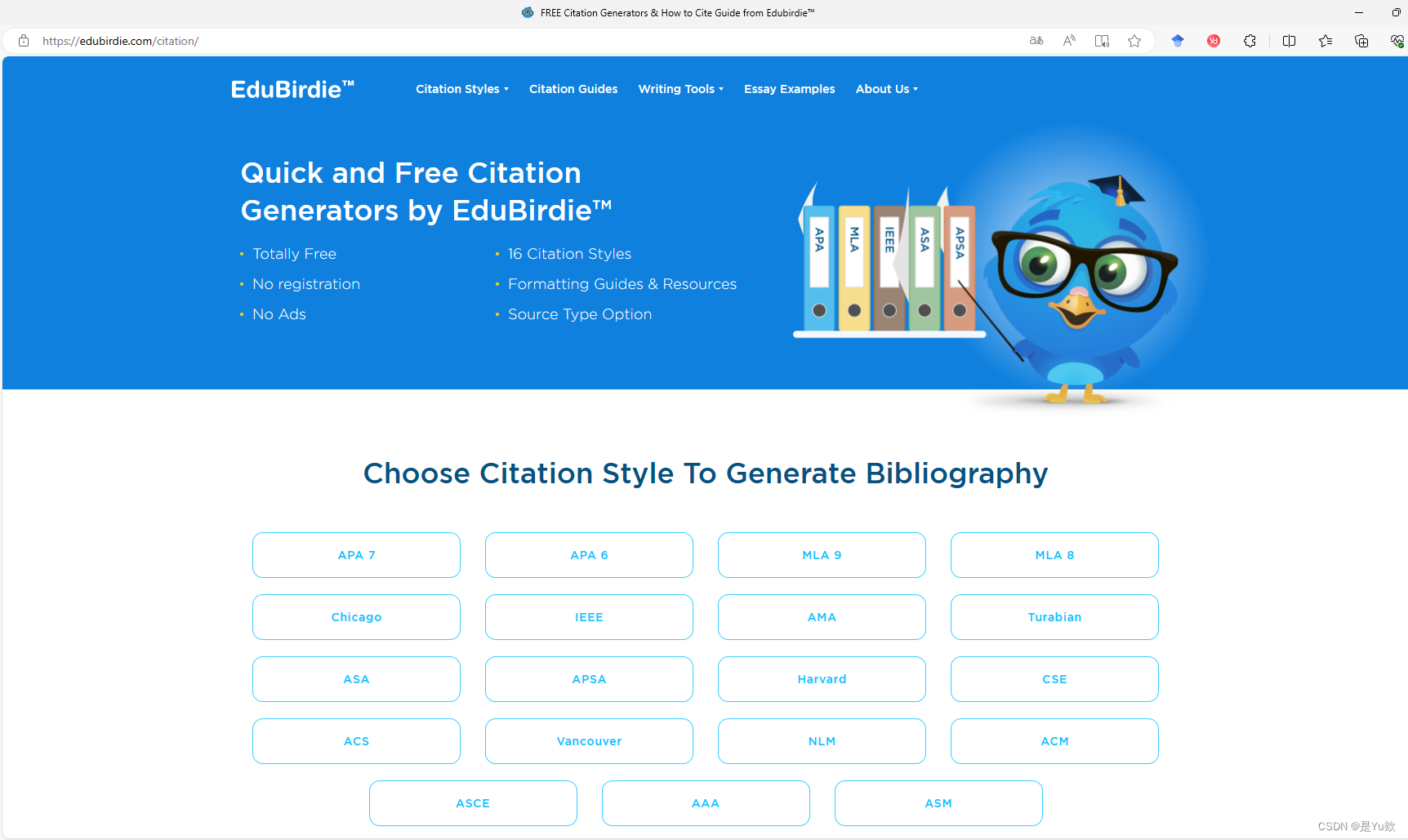
【latex】在Overleaf的IEEE会议模板中,快速插入参考文献
【LaTeX】在Overleaf的IEEE会议模板中,快速插入参考文献 写在最前面第一步:在文献检索网站导出引用文献的bib文件第二步:编辑overleaf模版方法二:EduBirdie生成参考文献(补充)使用LaTeX在Overleaf的IEEE会议…...
)
java反射之Field用法(获取对象的字段名和属性值)
一、概述 Field是一个类,位于java.lang.reflect包下。在Java反射中Field类描述的是类的属性信息,功能包括: 获取当前对象的成员变量的类型 对成员变量重新设值 二、如何获取Field类对象 getField(String name): 获取类特定的方法,…...

Java Web(三)--CSS
介绍 为什么需要: 在没有 CSS 之前,想要修改 HTML 元素的样式需要为每个 HTML 元素单独定义样式属性,费心费力;CSS 可以让 html 元素(内容) 样式(CSS)分离,提高web 开发的工作效率(针对前端开发),从而…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...
