上海计算机学会12月月赛 丙组题解
上海计算机学会 12 月月赛 丙组题解
涉及知识点:数学、字符串、模拟、裴蜀定理、宽度优先搜索、动态规划
比赛链接:https://iai.sh.cn/contest/58
第一题:T1数砖数
标签:数学
题意:给定一种 2 2 2x 2 2 2的瓷砖,样式为
##
.#
用瓷砖,从平面左上角出发,将整个平面铺满。形如:
################
.#.#.#.#.#.#.#.#
################
.#.#.#.#.#.#.#.#
################
.#.#.#.#.#.#.#.#
################
.#.#.#.#.#.#.#.#
给定 n n n行 m m m列的区域,求这块区域中 # \# #的数目。( 1 < = n , m < = 10000 1<=n,m<=10000 1<=n,m<=10000)
题解:考虑从整块区域中删掉 . . .的数目。观察发现偶数行、奇数列才有 . . .,自己手玩几组数据能够得到 . . .的数目是 ( n / 2 ) ∗ ( ( m + 1 ) / 2 ) (n/2)*((m+1)/2) (n/2)∗((m+1)/2)。
代码:
#include <bits/stdc++.h>
using namespace std;int main() {int n, m;cin >> n >> m;cout << n * m - (n / 2) * ((m + 1) / 2);return 0;
}
第二题:T2移动复位
标签:字符串、模拟
题意:给定一个二维平面上的顶点,然后进行一系列指令操作,指令操作以字符串的形式给出:
R R R 表示该点沿 X X X 轴坐标正方向移动了一个单位
L L L 表示该点沿 X X X 轴坐标负方向移动了一个单位
U U U 表示该点沿 Y Y Y 轴坐标正方向移动了一个单位
D D D 表示该点沿 Y Y Y 轴坐标负方向移动了一个单位
求这些指令执行完之后,至少再增加多少条指令能让这个点返回起点(原来的位置)。
题解:每次都是上下左右移动一个位置坐标,假设原来起点在原点( 0 , 0 0,0 0,0),最少指令数,即求当前坐标( x , y x,y x,y)与原点的曼哈顿距离: ∣ x ∣ + ∣ y ∣ |x|+|y| ∣x∣+∣y∣。
我这边用了 m a p map map去统计了各个移动方向指令的数量,然后东西和南北方向分别做抵消,求绝对值。
曼哈顿距离:两点在南北⽅向上的距离加上在东西⽅向上的距离。
代码:
#include <bits/stdc++.h>
using namespace std;map<char, int> m;int main() {string s;cin >> s;for (int i = 0; i < s.size(); i++) {m[s[i]]++;}cout << abs(m['L'] - m['R']) + abs(m['U'] - m['D']) << endl;return 0;
}
第三题:T3数轴旅行
标签:裴蜀定理
题意:初始位置在 x = 0 x=0 x=0,要去 x = d x=d x=d的位置,给定 n n n个整数 a 1 , a 2 , a 3 . . . , a n a_1,a_2,a_3...,a_n a1,a2,a3...,an,表示每次可以往左移动 a i a_i ai个单位或者往右移动 a i a_i ai个单位,求最后能不到达 x = d x=d x=d的位置。
( 1 < = n < = 1 0 5 , 1 < = a i < = 1 0 9 , − 1 0 9 < = d < = 1 0 9 1<=n<=10^5,1<=a_i<=10^9,-10^9<=d<=10^9 1<=n<=105,1<=ai<=109,−109<=d<=109)
题解:经典裴蜀定理题,有兴趣的可以去看看证明,我这边直接说定理和结论。
裴蜀定理:对于 x x x, y y y的二元一次不定方程 a x + b y = c ax+by=c ax+by=c,其有解的充要条件为 g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c。
( g c d ( a , b ) ∣ c gcd(a,b)|c gcd(a,b)∣c这个数学表示为 c c c能被 g c d ( a , b ) gcd(a,b) gcd(a,b)整除)
由基础定理我们可以得到一个推论:
对于不定方程 x 1 y 1 + x 2 y 2 + . . . + x n y n = k x_1y_1+x_2y_2+...+x_ny_n=k x1y1+x2y2+...+xnyn=k, ∀ y i ∈ Z \forall y_i \in \Z ∀yi∈Z,其有解的充要条件为 gcd { x i } ∣ k \gcd\{x_i\}\mid k gcd{xi}∣k。
回到本题我们可以写出这个式子, y i y_i yi可以是 − 1 -1 −1和 1 1 1:
a 1 y 1 + a 2 y 2 + . . . + a n y n = d a_1y1+a_2y_2+...+a_ny_n=d a1y1+a2y2+...+anyn=d
那么问题就转变成了 d d d能否被 [ 所有 a i a_i ai的最大公约数 ] 整除,能整除就有解,反之无解。
代码:
#include <bits/stdc++.h>
using namespace std;typedef long long ll;ll gcd(ll a, ll b) {if (b == 0) return a;return gcd(b, a % b);
}int main() {ll n, a, d, g = 0;cin >> n >> d;for (int i = 1; i <= n; i++) {cin >> a;g = gcd(g, a);}if (d % g == 0) cout << "Yes";else cout << "No";return 0;
}
第四题:T4迷宫
标签:宽度优先搜索
题意:给定 n n nx m m m由 # \# #(墙)、 . . .(空地)组成的地图,求从左上角到右下角的最少步数,每次只允许上下左右移动一格,不允许走出地图和走到 # \# #(墙)上。
题解:BFS 模板题,判断下一个能否走的点,经典三要素:
- 下个点是否是障碍物(宽泛来说是题目中的限制条件)
- 下个点是否走过(避免死循环)
- 下个点是否在地图内
代码:
#include <bits/stdc++.h>
using namespace std;int n, m;
int dx[4] = {0, 0, -1, 1};
int dy[4] = {-1, 1, 0, 0};char a[1005][1005];
bool vis[1005][1005];
struct node {int x, y, step;
};void bfs() {queue <node> q;vis[1][1] = 1;q.push({1, 1, 0});while (!q.empty()) {node u = q.front();q.pop();if (u.x == n && u.y == m) {cout << u.step << endl;return ;}for (int i = 0; i < 4; i++) {int nx = u.x + dx[i];int ny = u.y + dy[i];if (nx < 1 || nx > n || ny < 1 || ny > m) continue;if (vis[nx][ny] || a[nx][ny] == '#') continue;vis[nx][ny] = 1;q.push({nx, ny, u.step + 1});}}cout << "No solution" << endl;
}int main() {cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];bfs();return 0;
}
第五题:T5特定的串
标签:动态规划
题意:给定 01 01 01串,可以修改其中任意一个字符,把 0 0 0变成 1 1 1,把 1 1 1变成 0 0 0,不能删除或者增加 01 01 01字符,求最少修改个数,使得给定序列中不含特定子串 110 110 110。
题解:
贪心 90 90 90 分解法:比较容易想到的一个思路是把 11 11 11变成 10 10 10,或者把所有 0 0 0变成 1 1 1。
这个思路有以下几个反例:
101111101 101111101 101111101(这个只需要把后面的那个 0 0 0改成 1 1 1)
1100111101 1100111101 1100111101(这个可以把第 2 2 2个 1 1 1改成 0 0 0,最后那个 0 0 0改成 1 1 1)
像第二个反例,我们需要思考把两种贪心策略进行结合。
#include <bits/stdc++.h>
using namespace std;int main() {int n, num = 0; // num: 连续1的个数// c1: 11110变成10100// c2: 11011变成11111int c1 = 0, c2 = 0;string s;cin >> n >> s;for (int i = 0; i < n; i++) {if (s[i] == '0') {c2++;c1 += num / 2;num = 0;} else {num++;}}cout << min(c1, c2) << endl;return 0;
}
// 9
// 101111101// 10
// 1100111101
动态规划解法:
d p [ i ] [ 0 / 1 ] [ 0 / 1 ] dp[i][0/1][0/1] dp[i][0/1][0/1]:以第 i i i位为结尾,使得前 i i i个字符中不包含 110 110 110,且第 i i i位是 0 0 0或 1 1 1,第 i − 1 i-1 i−1位是 0 0 0或 1 1 1的最少修改个数。
考虑状态转移:
一、如果 s [ i ] s[i] s[i]修改成 0 0 0
- d p [ i ] [ 0 ] [ 0 ] dp[i][0][0] dp[i][0][0]( s [ i ] = 0 , s [ i − 1 ] = 0 s[i]=0,s[i-1]=0 s[i]=0,s[i−1]=0)可以从 s [ i − 2 ] = 0 / 1 s[i-2]=0/1 s[i−2]=0/1转移过来,即 d p [ i ] [ 0 ] [ 0 ] = m i n ( d p [ i − 1 ] [ 0 ] [ 0 ] , d p [ i − 1 ] [ 0 ] [ 1 ] ) dp[i][0][0] = min(dp[i-1][0][0], dp[i-1][0][1]) dp[i][0][0]=min(dp[i−1][0][0],dp[i−1][0][1])
- d p [ i ] [ 0 ] [ 1 ] dp[i][0][1] dp[i][0][1]( s [ i ] = 0 , s [ i − 1 ] = 1 s[i]=0,s[i-1]=1 s[i]=0,s[i−1]=1)只能从 s [ i − 2 ] = 0 s[i-2]=0 s[i−2]=0转移过来,即 d p [ i ] [ 0 ] [ 0 ] = d p [ i − 1 ] [ 1 ] [ 0 ] dp[i][0][0] = dp[i-1][1][0] dp[i][0][0]=dp[i−1][1][0]
二、如果 s [ i ] s[i] s[i]修改成 1 1 1
那不管是 001 001 001、 101 101 101、 111 111 111 011 011 011都是可以的。所以
d p [ i ] [ 1 ] [ 0 ] = m i n ( d p [ i − 1 ] [ 0 ] [ 0 ] , d p [ i − 1 ] [ 0 ] [ 1 ] ) dp[i][1][0] = min(dp[i-1][0][0], dp[i-1][0][1]) dp[i][1][0]=min(dp[i−1][0][0],dp[i−1][0][1])
d p [ i ] [ 1 ] [ 1 ] = m i n ( d p [ i − 1 ] [ 1 ] [ 0 ] , d p [ i − 1 ] [ 1 ] [ 1 ] ) dp[i][1][1] = min(dp[i-1][1][0], dp[i-1][1][1]) dp[i][1][1]=min(dp[i−1][1][0],dp[i−1][1][1])
然后再上面转移的过程中要考虑 s [ i ] s[i] s[i]是否修改,所以要把这个修改的代价都带上。
最后从 d p [ n − 1 ] dp[n-1] dp[n−1]的四种情况里面取最小值就可以了。
代码:
#include <bits/stdc++.h>
using namespace std;const int N = 5e5 +10;
char s[N];
int dp[N][2][2];
// 以第i位为结尾,使得前i个字符中不包含110,
// 且第i位是0或1,第i-1位是0或1的最少修改个数int main() {int n;cin >> n >> s;int s0 = s[0] - '0', s1 = s[1] - '0';dp[1][s1][s0] = 0;dp[1][s1^1][s0] = dp[1][s1][s0^1] = 1;dp[1][s1^1][s0^1] = 2;for (int i = 2; i < n; i++) {int d = 0;// s[i]修改成0if (s[i] != '0') d = 1;dp[i][0][0] = min(dp[i-1][0][0], dp[i-1][0][1]) + d;dp[i][0][1] = dp[i-1][1][0] + d;// s[i]修改成1d = 0;if (s[i] != '1') d = 1;dp[i][1][0] = min(dp[i-1][0][0], dp[i-1][0][1]) + d;dp[i][1][1] = min(dp[i-1][1][0], dp[i-1][1][1]) + d;}cout << min(min(dp[n-1][0][0], dp[n-1][0][1]), min(dp[n-1][1][0], dp[n-1][1][1]));return 0;
}
相关文章:

上海计算机学会12月月赛 丙组题解
上海计算机学会 12 月月赛 丙组题解涉及知识点:数学、字符串、模拟、裴蜀定理、宽度优先搜索、动态规划 比赛链接:https://iai.sh.cn/contest/58 第一题:T1数砖数 标签:数学题意:给定一种 2 2 2x 2 2 2的瓷砖&#…...
nextjs中beforePopState使用
在某些情况下,希望监听popstate并在路由器对其进行操作之前执行某些操作。可以使用beforePopState。 在Next.js中,beforePopState是一个可选的生命周期函数,用于在浏览器的历史记录发生更改之前执行一些操作。具体来说,beforePopS…...
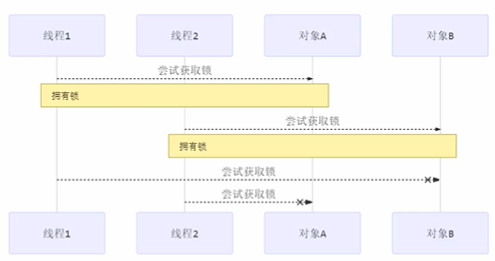
【并发编程】活锁
📝个人主页:五敷有你 🔥系列专栏:并发编程 ⛺️稳重求进,晒太阳 活锁 定义:活锁出现在两个线程互相改变对象的结束条件,最后谁也无法结束 代码示例 public class TestLiveLock {stati…...

CSMM和CMMI之间有什么区别?
CSMM(软件能力成熟度评估)和CMMI(能力成熟度模型集成)都是软件行业中用于评估和提高企业软件开发过程成熟度的模型。它们之间的主要区别在于起源、定位、适应范围和具体内容。 1. 起源与定位: - CMMI是由美国卡耐基…...

企业面临的典型网络安全风险及其防范策略
网络安全威胁是一种技术风险,会削弱企业网络的防御能力,危及专有数据、关键应用程序和整个IT基础设施。由于企业面临着广泛的威胁,因此通过监控和缓解最关键的威胁和漏洞。网络安全问题有七大类,包括多种威胁,以及团队…...
JavaScript进阶:WebAPIs重点知识整理1
目录 1 DOM修改元素内容 2 DOM修改元素常见属性 3 修改元素样式属性 3.1 通过style修改元素样式 3.2 通过类名className修改元素样式 3.3 通过classList修改元素样式 4 操作表单元素属性 5 自定义属性 6 定时器 7 事件监听 7.1 点击事件 click 7.2 鼠mouseenter和移…...

【Nginx】使用自生成证书配置nginx代理https
使用Nginx代理HTTPS请求并使用自签名证书,可以按照以下步骤进行配置: 生成自签名证书: 打开终端或命令提示符,并导航到Nginx配置文件所在的目录。运行以下命令生成自签名证书和私钥: openssl req -x509 -nodes -days 3…...
【Linux】文件周边001之系统文件IO
👀樊梓慕:个人主页 🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》《LeetCode刷题笔记》《实训项目》《C》《Linux》《算法》 🌝每一个不曾起舞的日子,都是对生命的辜负 目录 前言 1.C语言文件IO 1.1…...
防火墙接口配置实验
1、搭建拓扑 2、给云端添加网络,来实现真机与虚拟机的连接 3、 给防火墙g0/0/0口配置IP,由于我云端绑定的是192.168.100.10,所以这里IP配置为192.168.100.1/24,使用命令开启防火墙远程连接的服务,之后便可通过web远程登陆防火墙 …...

《WebKit 技术内幕》学习之五(4): HTML解释器和DOM 模型
4 影子(Shadow)DOM 影子 DOM 是一个新东西,主要解决了一个文档中可能需要大量交互的多个 DOM 树建立和维护各自的功能边界的问题。 4.1 什么是影子 DOM 当开发这样一个用户界面的控件——这个控件可能由一些 HTML 的标签元素…...
SpringBoot+Vue充电桩管理系统 附带详细运行指导视频
文章目录 一、项目演示二、项目介绍三、运行截图四、主要代码1. 分页获取预约数据代码2.保存预约信息代码3.修改订单状态代码 一、项目演示 项目演示地址: 视频地址 二、项目介绍 项目描述:这是一个基于SpringBootVue框架开发的充电桩管理系统。首先&…...
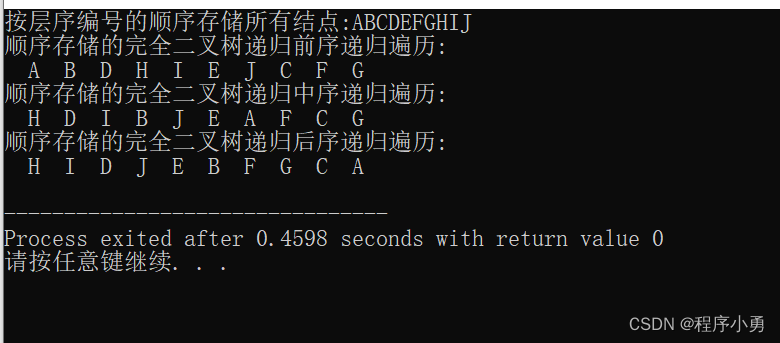
【数据结构】二叉树算法讲解(定义+算法原理+源码)
博主介绍:✌全网粉丝喜爱、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦! 🍅附上相关C语言版源码讲解🍅 ὄ…...
是什么?根组件模板又是什么?)
Vue3基础:挂载事例方法.mount()是什么?根组件模板又是什么?
.mount() <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Vue 3 演示</title> </head>…...
Unity渲染与Shader篇 【全面总结 | 持续更新】)
Unity 面试篇|(七)Unity渲染与Shader篇 【全面总结 | 持续更新】
目录 1.问一个Terrain,分别贴3张,4张,5张地表贴图,渲染速度有什么区别?为什么?2.什么是LightMap?3.MipMap是什么,作用?4.请问alpha test在何时使用?能达到什么…...

记录一些多维数组的方法
文章目录 前言一、获取多维数组的数据二、多维数组自带的方法总结 前言 验证过程中,我们经常会用到多维数组存储数据,本文主要记录一下,如何去获取我们需要的数据,以及多维数组自带的一些方法。 一、获取多维数组的数据 获取多维…...

Linux:gcc的相关知识
目录 gcc的翻译(编译)过程: 预处理: 条件编译: 编译: 汇编&链接: 什么是链接? 安装静态库: 静态库的使用: 动态静态的对比: 优缺对比…...

Linux的奇妙冒险———vim的用法和本地配置
vim的用法和本地配置 一.vim的组成和功能。1.什么是vim2.vim的多种模式 二.文本编辑(普通模式)的快捷使用1.快速复制,粘贴,剪切。2.撤销,返回上一步操作3.光标的控制4.文本快捷变换5.批量化操作和注释 三.底行模式四.v…...
微信小程序底部按钮适配iPhoneX以上,显示遮挡问题
只需要在给底部按钮加个样式 /* 底部导航栏容器 */ .button-box {/* 使用 safe-area-inset-bottom 属性适配 iPhone X 及以上型号设备 */padding-bottom: constant(safe-area-inset-bottom);padding-bottom: env(safe-area-inset-bottom);/* 其他样式属性 */ }iPhone6/7/8效果 …...
)
Qt容器QMap(映射)
插入数据 QMap<QString,QString> infoMap; //第一个是key 第二个是valueinfoMap.insert("王祖蓝","163cm");infoMap.insert("Anglebaby","168cm");infoMap["易烊千玺"] "173cm(成长中)";infoMap["姚…...

AI时代的创新工具:如何利用AI生成独具个性的XMind思维导图?
哈喽,大家好,我是木头左,物联网搬砖工一名,致力于为大家淘出更多好用的AI工具! 背景 随着互联网的发展,越来越多的人开始使用Markdown来编写文档。Markdown是一种轻量级的标记语言,它允许人们使…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
