【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
文章目录
- 1.4 主应力空间、八面体应力
- 1.5 应变分析
- 1.6 特殊应力、应变定义
1.4 主应力空间、八面体应力
一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描述问题将不失一般性,该坐标系如下图4,我们称之为主应力空间。我们考察等倾面组成的八面体,图中O’P点为等倾面ABC上面的应力向量 ( p 1 , p 2 , p 3 ) (p_1,p_2,p_3) (p1,p2,p3),八面体为等倾面八面体,即面ABC的法线方向余弦为 ( 1 3 , 1 3 , 1 3 ) (\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (31,31,31)。将O’P分解
O ’ P ‾ = O ’ Q ‾ + O ’ N ‾ (25) \overline {O’P}=\overline {O’Q}+\overline{O’N}\tag{25} O’P=O’Q+O’N(25)
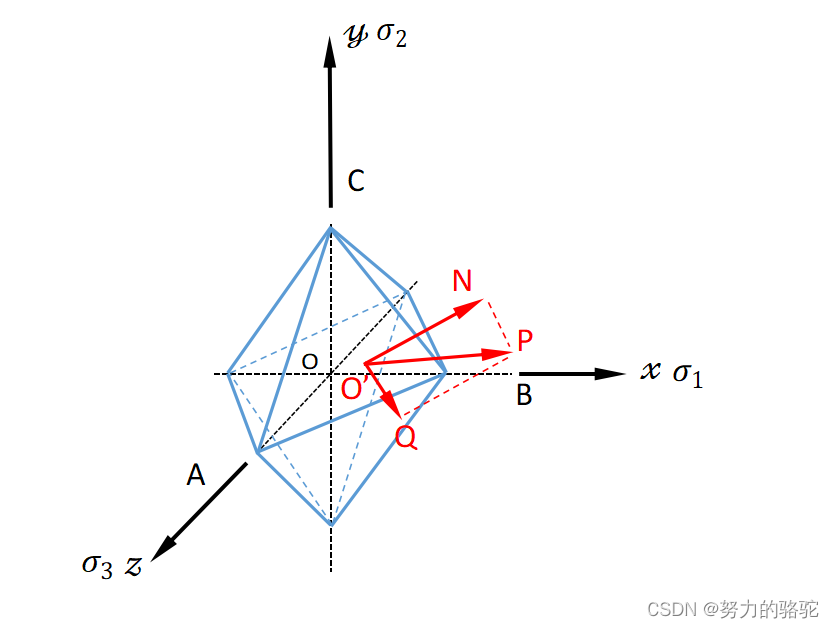
图 4 八面体 图4八面体 图4八面体
取等倾面和三个轴的坐标面组成的四面体为研究对象,如下图5所示。
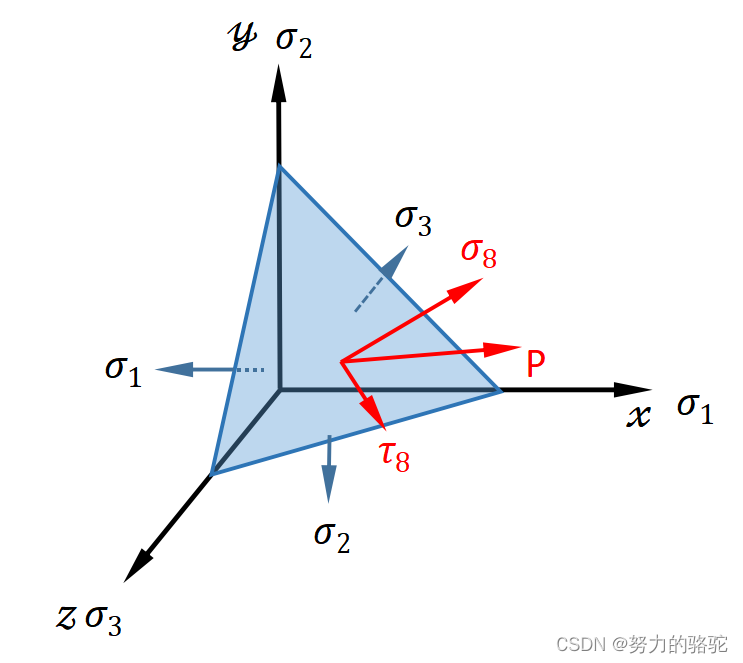
图 5 等倾面四面体 图5等倾面四面体 图5等倾面四面体
根据斜面应力公式 p j = σ i j n i p_j=\sigma_{ij}n_i pj=σijni,不难得到以下关系式(矩阵形式)
[ p 1 p 2 p 3 ] = [ σ 1 0 0 0 σ 2 0 0 0 σ 2 ] [ n 1 n 2 n 3 ] (26) \begin{bmatrix} p_1 \\ p_2\\p_3 \end{bmatrix}=\begin{bmatrix} \sigma_1 & 0 & 0\\ 0 & \sigma_2 & 0 \\0 & 0 & \sigma_2 \end{bmatrix}\begin{bmatrix} n_1 \\ n_2\\n_3 \end{bmatrix}\tag{26} p1p2p3 = σ1000σ2000σ2 n1n2n3 (26)
其中 ( n 1 , n 2 , n 3 ) = ( 1 3 , 1 3 , 1 3 ) (n_1 ,n_2,n_3)=(\frac{1}{\sqrt 3},\frac{1}{\sqrt 3},\frac{1}{\sqrt 3}) (n1,n2,n3)=(31,31,31)为等倾面的法线方向余弦。
那么,有
σ 8 = [ n 1 n 2 n 3 ] [ p 1 p 2 p 3 ] = σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 = 1 3 ( σ 1 + σ 2 + σ 3 ) = 1 3 I 1 (27) \sigma_8 = \begin{bmatrix} n_1 & n_2 & n_3 \end{bmatrix}\begin{bmatrix} p_1 \\ p_2\\p_3 \end{bmatrix}=\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2=\frac{1}{3}(\sigma_1+\sigma_2+\sigma_3)=\frac{1}{3}I_1 \tag{27} σ8=[n1n2n3] p1p2p3 =σ1n12+σ2n22+σ3n32=31(σ1+σ2+σ3)=31I1(27)
八面体相应的剪应力为
τ 8 = p 2 − σ 8 2 = p 1 2 + p 2 2 + p 3 2 − ( σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 ) 2 = σ 1 2 n 1 2 + σ 2 2 n 2 2 + σ 3 2 n 3 2 − ( σ 1 n 1 2 + σ 2 n 2 2 + σ 3 n 3 2 ) 2 = 1 3 ( σ 1 2 + σ 2 2 + σ 3 2 ) − 1 9 ( σ 1 + σ 2 + σ 3 ) 2 = 1 3 3 ( σ 1 2 + σ 2 2 + σ 3 2 ) − ( σ 1 2 + σ 2 2 + σ 3 2 + 2 σ 1 σ 2 + 2 σ 1 σ 3 + 2 σ 2 σ 3 ) = 1 3 ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 = 2 3 J 2 = 1 3 s i j s i j (28) \tau_8 = \sqrt{p^2-\sigma_8^2}=\sqrt{p_1^2+p_2^2+p_3^2-(\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2)^2}\\ =\sqrt{\sigma_1^2n_1^2+\sigma_2^2n_2^2+\sigma_3^2n_3^2-(\sigma_1n_1^2+\sigma_2n_2^2+\sigma_3n_3^2)^2}\\ =\sqrt{\frac{1}{3}(\sigma_1^2+\sigma_2^2+\sigma_3^2)-\frac{1}{9}(\sigma_1+\sigma_2+\sigma_3)^2}\\ =\frac{1}{3}\sqrt{3(\sigma_1^2+\sigma_2^2+\sigma_3^2)-(\sigma_1^2+\sigma_2^2+\sigma_3^2+2\sigma_1\sigma_2+2\sigma_1\sigma_3+2\sigma_2\sigma_3)}\\ =\frac{1}{3}\sqrt{(\sigma_1-\sigma_2)^2+(\sigma_1-\sigma_3)^2+(\sigma_2-\sigma_3)^2}=\sqrt{\frac{2}{3}J_2}=\sqrt{\frac{1}{3}s_{ij}s_{ij}} \tag{28} τ8=p2−σ82=p12+p22+p32−(σ1n12+σ2n22+σ3n32)2=σ12n12+σ22n22+σ32n32−(σ1n12+σ2n22+σ3n32)2=31(σ12+σ22+σ32)−91(σ1+σ2+σ3)2=313(σ12+σ22+σ32)−(σ12+σ22+σ32+2σ1σ2+2σ1σ3+2σ2σ3)=31(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2=32J2=31sijsij(28)
1.5 应变分析
应变分析的内容同应力分析内容,只是注意一点,应变张量和工程应变在剪应变分量是不同的,定义如下。
[ ε x x ε y x ε z x ε x y ε y y ε z y ε x z ε y z ε z z ] = [ ε x x 1 2 γ y x 1 2 γ z x 1 2 γ x y ε y y 1 2 γ z y 1 2 γ x z 1 2 γ y z ε z z ] (29) \begin{bmatrix} \varepsilon_{xx} & \varepsilon_{yx} & \varepsilon_{zx}\\ \varepsilon_{xy} & \varepsilon_{yy} & \varepsilon_{zy}\\ \varepsilon_{xz} & \varepsilon_{yz} & \varepsilon_{zz} \end{bmatrix}= \begin{bmatrix} \varepsilon_{xx} & \frac{1}{2}\gamma_{yx} & \frac{1}{2}\gamma_{zx}\\ \frac{1}{2}\gamma_{xy} & \varepsilon_{yy} & \frac{1}{2}\gamma_{zy}\\ \frac{1}{2}\gamma_{xz} & \frac{1}{2}\gamma_{yz} & \varepsilon_{zz} \end{bmatrix}\tag{29} εxxεxyεxzεyxεyyεyzεzxεzyεzz = εxx21γxy21γxz21γyxεyy21γyz21γzx21γzyεzz (29)
同样定义应变偏张量,有如下形式
[ e x x e y x e z x e x y e y y e z y e x z e y z e z z ] = [ ε x x ε y x ε z x ε x y ε y y ε z y ε x z ε y z ε z z ] − [ ε m 0 0 0 ε m 0 0 0 ε m ] (30) \begin{bmatrix} e_{xx} & e_{yx} & e_{zx}\\ e_{xy} & e_{yy} & e_{zy}\\ e_{xz} & e_{yz} & e_{zz} \end{bmatrix}= \begin{bmatrix} \varepsilon_{xx} & \varepsilon_{yx} & \varepsilon_{zx}\\ \varepsilon_{xy} & \varepsilon_{yy} & \varepsilon_{zy}\\ \varepsilon_{xz} & \varepsilon_{yz} & \varepsilon_{zz} \end{bmatrix}-\begin{bmatrix} \varepsilon_{m} & 0 & 0\\ 0 & \varepsilon_{m} & 0\\ 0 & 0 & \varepsilon_{m} \end{bmatrix}\tag{30} exxexyexzeyxeyyeyzezxezyezz = εxxεxyεxzεyxεyyεyzεzxεzyεzz − εm000εm000εm (30)
其中 ε m = 1 3 ( ε x x + ε y y + ε z z ) \varepsilon_{m}=\frac{1}{3}(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}) εm=31(εxx+εyy+εzz)
1.6 特殊应力、应变定义
定义应力强度或等效应力 σ ‾ \overline\sigma σ为
σ ‾ = 3 J 2 = 3 2 s i j s i j = 1 2 [ ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 ] = 1 2 [ ( σ x x − σ y y ) 2 + ( σ x x − σ z z ) 2 + ( σ y y − σ z z ) 2 + 6 ( τ x z 2 + τ x y 2 + τ y z 2 ) ] (31) \overline\sigma=\sqrt{3J_2}=\sqrt{\frac{3}{2}s_{ij}s_{ij}}\\ =\sqrt{\frac{1}{2}[(\sigma_{1}-\sigma_{2})^2+(\sigma_{1}-\sigma_{3})^2+(\sigma_{2}-\sigma_{3})^2]}\\ =\sqrt{\frac{1}{2}[(\sigma_{xx}-\sigma_{yy})^2+(\sigma_{xx}-\sigma_{zz})^2+(\sigma_{yy}-\sigma_{zz})^2+6(\tau_{xz}^2+\tau_{xy}^2+\tau_{yz}^2)]} \tag{31} σ=3J2=23sijsij=21[(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2]=21[(σxx−σyy)2+(σxx−σzz)2+(σyy−σzz)2+6(τxz2+τxy2+τyz2)](31)
定义应变强度或等效应变 ε ‾ \overline \varepsilon ε为
ε ‾ = 2 3 e i j e i j (32) \overline \varepsilon=\sqrt{\frac{2}{3}e_{ij}e_{ij}} \tag{32} ε=32eijeij(32)
定义剪切等效应力 T ‾ \overline T T为
T ‾ = 1 2 s i j s i j (33) \overline T=\sqrt{\frac{1}{2}s_{ij}s_{ij}} \tag{33} T=21sijsij(33)
定义剪切等效应变 Γ ‾ \overline\Gamma Γ为
Γ ‾ = 2 e i j e i j (34) \overline\Gamma=\sqrt{2e_{ij}e_{ij}} \tag{34} Γ=2eijeij(34)
加上上面定义的八面体剪应力、八面体剪应变
τ 8 = 1 3 s i j s i j γ 8 = 4 3 e i j e i j (35) \tau_8=\sqrt{\frac{1}{3}s_{ij}s_{ij}}\\ \gamma_8=\sqrt{\frac{4}{3}e_{ij}e_{ij}}\tag{35} τ8=31sijsijγ8=34eijeij(35)
至于为什么定义这些应力应变,我们在后面再介绍。
相关文章:

【小呆的力学笔记】弹塑性力学的初步认知二:应力应变分析(2)
文章目录 1.4 主应力空间、八面体应力1.5 应变分析1.6 特殊应力、应变定义 1.4 主应力空间、八面体应力 一点的应力状态不论如何变化,其主应力和主方向一致的话,该点的应力状态就是唯一确定的。因此,我们用主应力方向建立一个三维坐标系来描…...
【学网攻】 第(6)节 -- 三层交换机实现VLAN间路由
文章目录 【学网攻】 第(1)节 -- 认识网络【学网攻】 第(2)节 -- 交换机认识及使用【学网攻】 第(3)节 -- 交换机配置聚合端口【学网攻】 第(4)节 -- 交换机划分Vlan【学网攻】 第(5)节 -- Cisco VTP的使用 前言 网络已经成为了我们生活中不可或缺的一部分,它连接了…...

C++之内联函数
函数调用在执行时,首先要在栈中为形参和局部变量分配存储空间,然后还要将实参的值复制给形参,接下来还要将函数的返回地址(该地址指明了函数执行结束后,程序应该回到哪里继续执行)放入栈中,最后…...

【Bugku-web】alert
1.打开场景 2.按"CtrlU"查看源代码 3.翻到页面最末尾会有一个HTML实体编码,用在线工具在线Html实体编码解码后,得到flag值。...
QQ数据包解密
Windows版qq数据包格式: android版qq数据包格式: 密钥:16个0 算法:tea_crypt算法 pc版qq 0825数据包解密源码: #include "qq.h" #include "qqcrypt.h" #include <WinSock2.h> #include…...

腾讯云上linux系统使用nginx,flask构建个人网站SSL证书过期换证书的操作步骤
ssl证书过期的时候,一般腾讯云提前一段时间给通知,让更换ssl证书,现在一般都可以免费更换,一般是一年期的,审核通过之后,需要下载nginx版本的证书,我的是4个文件,替换到nginx/cert文…...

git-clone的single-branch操作回退
(Owed by: 春夜喜雨 http://blog.csdn.net/chunyexiyu) 最近使用git越来越多,一些git的功能使用也更熟悉了一些。 之前使用了single-branch下载分支,后来想取消掉,但怎么做呢,查了一些资料之后,了解到了怎么做&#x…...
03 SpringBoot实战 -微头条之首页门户模块(跳转某页面自动展示所有信息+根据hid查询文章全文并用乐观锁修改阅读量)
1.1 自动展示所有信息 需求描述: 进入新闻首页portal/findAllType, 自动返回所有栏目名称和id 接口描述 url地址:portal/findAllTypes 请求方式:get 请求参数:无 响应数据: 成功 {"code":"200","mes…...

YOCTO基础 - 创建meta层与bb文件
背景 在当前的嵌入式系统开发项目中,我们面临着构建定制化 Linux 发行版以满足项目需求的挑战。我们需要在目标硬件上运行一个轻量级、高度定制化的 Linux 映像,并确保它包含我们项目中所需的特定软件包和功能。为了实现这一目标,我们选择了…...

网络电视盒子哪个好?博主分享超高性价比网络电视盒子推荐
电视盒子是我们使用最多的数码产品,年货节很多朋友在纠结网络电视盒子哪个好,我这次的测评产品就是电视盒子,按照18款电视盒子的深度测评结果整理了网络电视盒子推荐,想知道网络电视盒子哪个好可以看看下面这五款电视盒子。 一&am…...

leetcode 刷题2
二分查找的绝妙运用: 看到有序数列,算法复杂度 0033. 搜索旋转排序数组 class Solution { public:int search(vector<int>& nums, int target) {int left 0;int right nums.size() - 1;while (left < right) {int mid left (right - …...
2-SAT问题相关理论和算法
前言 SAT 问题简介 SAT是可满足性、适定性(Satisfiability)问题的简称。一般形式为k-适定性问题或k-可满足性问题,简称 k-SAT。 何为布尔可满足性问题?给定一条真值表达式,包含逻辑变量、逻辑与、逻辑或以及非运算符,如&#x…...
【大数据精讲】全量同步与CDC增量同步方案对比
目录 背景 名词解释 问题与挑战 FlinkCDC DataX 工作原理 调度流程 五、DataX 3.0六大核心优势 性能优化 背景 名词解释 CDC CDC又称变更数据捕获(Change Data Capture),开启cdc的源表在插入INSERT、更新UPDATE和删除DELETE活动时…...

自定义通用返回对象
目的:给返回对象补充一些信息,告诉前端这个请求在业务层面上是成功还是失败,以及具体的描述信息。 我们需要自定义错误码(因为前端的HTTP状态码默认的值比较少)和正常错误返回类。 ErrorCode : package …...

从0开始python学习-51.pytest之接口加密封装
目录 MD5加密 base64加密 rsa加密 MD5加密 1. 封装加密方法 def md5_encode(self,data):data str(data).encode("utf-8")md5_data hashlib.md5(data).hexdigest()return md5_data 2. 写入需要使用加密的接口yaml用例 -request:method: posturl: http://192.168.…...

c++的命名空间
命名空间 一.c的关键字二.命名空间2.1 命名空间定义2.1 命名空间的使用2.1.1加命名空间名称及作用域限定符2.1.2使用using将命名空间中某个成员引入 三.标准命名空间std 一.c的关键字 c中一共有63个关键字 关键字11111asmdoifreturntrycontinueautodoubleinlineshorttypedeff…...
)
阿富汗塔利班兴起时的比赛代码3475:练85.3 删数问题(Noip1994)
【题目描述】 输入一个高精度的正整数n�,去掉其中任意s�个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的n�和s�,寻找一种方案使得剩下的数字组成的新数最小。 输出新的正整数。࿰…...

大数据平台红蓝对抗 - 磨利刃,淬精兵!
背景 目前大促备战常见备战工作:专项压测(全链路压测、内部压测)、灾备演练、降级演练、限流、巡检(监控、应用健康度)、混沌演练(红蓝对抗),如下图所示。随着平台业务越来越复杂&a…...
【2024-01-22】某极验3流程分析-滑块验证码
声明:该专栏涉及的所有案例均为学习使用,严禁用于商业用途和非法用途,否则由此产生的一切后果均与作者无关!如有侵权,请私信联系本人删帖! 文章目录 一、前言二、抓包流程分析1.刷新页面2.点击按钮进行验证…...

Laya2.13.3接入FGUI
下载与复制文件与Laya1.x类似,可以看我上一篇: Laya1.8.4接入FariyGui,以及其中踩的坑-CSDN博客 不同的是: 两个库文件需要在index.js中引入 新建一个脚本将fgui中搭建好的UI包引入: export default class GameApp…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
