【算法小记】——机器学习中的概率论和线性代数,附线性回归matlab例程
内容包含笔者个人理解,如果错误欢迎评论私信告诉我
线性回归matlab部分参考了up主DR_CAN博士的课程
机器学习与概率论
在回归拟合数据时,根据拟合对象,可以把分类问题视为一种简答的逻辑回归。在逻辑回归中算法不去拟合一段数据而是判断输入的数据是哪一个种类。有很多算法既可以实现线性回归也可以实现逻辑回归。
| 线性回归 | 逻辑回归 | |
|---|---|---|
| 目的 | 预测 | 分类 |
| y ( i ) y^{(i)} y(i) | 未知 | (0,1) |
| 函数 | 拟合函数 | 预测函数 |
| 参数计算方式 | 最小二乘法 | 极大似然估计 |
如何实现概率上的分布?
在概率论中当拥有一组足够大样本数据时,那么这组数据的期望和方差会收敛于这个数据分布的期望和方差。
对基本的切比雪夫不等式, E ( I ∣ X − μ ∣ > α ) = P ( ∣ X − μ ∣ ≥ α ) ≤ D X α 2 E(I_{\left|X-\mu \right|}>\alpha )=P(\left|X-\mu \right|\ge\alpha)\le\frac{DX}{\alpha^2} E(I∣X−μ∣>α)=P(∣X−μ∣≥α)≤α2DX
由此出发可以推导出切比雪夫大数定律、伯努利大数定律,中心极限定理等概率论的基石公式。
那么假如现在我们有一组样本数据,样布数据来自某个未知分布。是否可以找到一个含参函数,可以百分百拟合样本服从的分布?
∃ f ( X ∣ θ ) ? ⇒ lim ε → 0 + P ( ∣ f ( X ) − x ∣ < ε ) = 1 \exists f(X|\theta )?\Rightarrow \lim_{\varepsilon \to 0^+} P(|f(X)-x|<\varepsilon )=1 ∃f(X∣θ)?⇒ε→0+limP(∣f(X)−x∣<ε)=1
从这个问题出发,在统计学上我们已经认识了矩估计、极大似然估计两种方法来计算这个函数中的具体参数。
对计算机来说是否有其他方法?
- 多层判断:如果样本分布在有限空间内,总可以找到一个符合分布的树状判断结构,一层一层递推判断并构建新分支,最后得到完整的符合分布的判断结构。
- 迭代学习:通过循环输入样本参数,计算函数的输出是否符合要求,再根据差距大小,调整函数构成和参数值,最后得到函数结果。
树状判断很好理解,那迭代学习如何实现:
首先是需要知道函数计算得到的分布和实际的分布之间的差距。继续上面的公式我们可以再加入一个函数,用来计算当前函数结果是否准确
l o s s ( f ( x ∣ θ ) − F ( X ) ) loss (f(x|\theta )-F(X)) loss(f(x∣θ)−F(X))
我们把这样的函数称之为代价函数,在深度学习中也可称之为损失函数。当有样本和真确分布的答案时(有监督学习)可以直接计算函数输出到实际的距离。对于没有正确答案的回归时,此时变为求解函数到所有样本点之间的距离:
L ( x , θ ) = 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) L(x, \theta) = \frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)}) L(x,θ)=m1i=1∑m(f(x(i))−y(i))
当存在参数使得函数到所有样本距离最小的时候:
∃ θ ⇒ min L ( x , θ ) = min 1 m ∑ i = 1 m ( f ( x ( i ) ∣ θ ) − y ( i ) ) \exists\theta\Rightarrow\min L(x,\theta)=\min\frac{1}{m}\sum_{i=1}^m(f(x^{(i)}|\theta)-y^{(i)}) ∃θ⇒minL(x,θ)=minm1i=1∑m(f(x(i)∣θ)−y(i))
此时可以称之为找到了一个函数可以再概率上最大程度的拟合样本的分布情况。
机器学习中很多方法的目的就是,找到科学的方法,让计算机根据样本数据找到合适的函数 f 和合适的参数,并最终能够应用到新的场景对新样本做出预测或判断。
现在假设机器学习样本数据时直接使用上述的差值平均值作为代价,那如何求解参数来使差值最小?答案已经呼之欲出————梯度。 ∂ L ∂ θ = L ˙ ( x , θ ) = 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) ′ \frac{\partial L}{\partial \theta}=\dot{L} (x, \theta) = {\frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)})}' ∂θ∂L=L˙(x,θ)=m1i=1∑m(f(x(i))−y(i))′ 1 m ∑ i = 1 m ( f ( x ( i ) ) − y ( i ) ) θ ′ ⇒ 1 m ∑ i = 1 m ( f θ ′ ( x ( i ) ) − y ( i ) ) {\frac{1}{m}\sum_{i=1}^m(f(x^{(i)})-y^{(i)})}'_\theta \Rightarrow {\frac{1}{m}\sum_{i=1}^m(f'_\theta (x^{(i)})-y^{(i)})} m1i=1∑m(f(x(i))−y(i))θ′⇒m1i=1∑m(fθ′(x(i))−y(i))
计算梯度时,输入的样本是已知数据,需要变化的是函数的参数,通过计算代价函数对变量的梯度,就可以知道在输入样本的前提下,函数朝着什么方向变化参数能使输出的差值变小,此时计算机只需根据梯度更新参数。通过不断的循环这个步骤就达到了学习参数的目的。
通过上面的介绍,简单知道了学习的过程。实际上在机器学习中远没有这样简单,从函数结构,代价函数,到参数更新,输入输出等等,每一个环节都有着详细的内容和不同的方法来适应不同的数据场景。
机器学习与线性代数
矩阵的导数运算
在标量方程中偏导数的计算形式为: f ′ ( x ) = ∂ f ∂ x f'(x) = \frac{\partial f}{\partial x} f′(x)=∂x∂f 当二维的标量方程求偏导数时有: f ′ ( x 1 , x 2 ) = { d f ( x 1 , x 2 ) d x 1 d f ( x 1 , x 2 ) d x 2 f'(x_1, x_2)=\left\{\begin{matrix}\frac{\mathrm{d} f(x_1, x_2)}{\mathrm{d} x_1} \\\frac{\mathrm{d} f(x_1, x_2)}{\mathrm{d} x_2} \end{matrix}\right. f′(x1,x2)={dx1df(x1,x2)dx2df(x1,x2) 不妨可以将这样的偏导数写为向量形式,令 x ⃗ n = { x 1 , x 2 . . . . . . x n } \vec{x}_n = \left \{ x_1 , x_2 ......x_n \right\} xn={x1,x2......xn} 可以有n维方程的偏导数矩阵为: ∂ f ( x ⃗ ) ∂ x ⃗ = [ ∂ f ( x ⃗ ) ∂ x 1 ∂ f ( x ⃗ ) ∂ x 2 . . . ∂ f ( x ⃗ ) ∂ x n ] \frac{\partial f(\vec{x})}{\partial \vec{x}} =\begin{bmatrix}\frac{\partial f(\vec{x})}{\partial x_1} \\\frac{\partial f(\vec{x})}{\partial x_2} \\... \\\frac{\partial f(\vec{x})}{\partial x_n} \end{bmatrix} ∂x∂f(x)=⎣⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)...∂xn∂f(x)⎦⎥⎥⎥⎤ 当偏导数矩阵的行数与原方程的维度相同时称之为分母布局,列数和原方程的维度相同时称之为分子布局。
很多时候在执行反向传播计算参数更新时就是由于布局模式的不同会导致求得的矩阵维度不同,而不同维度的矩阵往往都不能直接进行计算,导致程序出错。当然除了上面说的n*1维方程,也可以是向量方程组的形式: ∂ f ( x ⃗ ) ∂ x ⃗ = [ f 1 ( x ⃗ ) f 2 ( x ⃗ ) . . . f m ( x ⃗ ) ] x ⃗ = [ x 1 x 2 . . . x n ] \frac{\partial f(\vec{x})}{\partial \vec{x}} =\begin{bmatrix} f_1(\vec{x} ) \\f_2(\vec{x} ) \\... \\f_m(\vec{x} ) \end{bmatrix} \quad \vec{x} = \begin{bmatrix} x_1 \\x_2 \\... \\x_n \end{bmatrix} ∂x∂f(x)=⎣⎢⎢⎡f1(x)f2(x)...fm(x)⎦⎥⎥⎤x=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤ 当使用分母布局时这样的向量方向方程组可以得到偏导数矩阵: ∂ f ( x ⃗ ) m ∂ x ⃗ n = [ ∂ f ( x ⃗ ) ∂ x 1 ∂ f ( x ⃗ ) ∂ x 2 . . . ∂ f ( x ⃗ ) ∂ x n ] = [ ∂ f 1 ( x ⃗ ) ∂ x 1 ∂ f 2 ( x ⃗ ) ∂ x 1 . . . ∂ f m ( x ⃗ ) ∂ x 1 . . . . . . . . . . . . ∂ f 1 ( x ⃗ ) ∂ x n . . . . . . ∂ f m ( x ⃗ ) ∂ x n ] n × m \frac{\partial f(\vec{x})_m}{\partial \vec{x}_n} =\begin{bmatrix} \frac{\partial f(\vec{x})}{\partial x_1} \\\frac{\partial f(\vec{x})}{\partial x_2} \\... \\\frac{\partial f(\vec{x})}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \frac{\partial f_1(\vec{x})}{\partial x_1} &\frac{\partial f_2(\vec{x})}{\partial x_1} &... &\frac{\partial f_m(\vec{x})}{\partial x_1} \\ ... &... &... &... \\ \frac{\partial f_1(\vec{x})}{\partial x_n} &... &... &\frac{\partial f_m(\vec{x})}{\partial x_n} \end{bmatrix}_{n\times m} ∂xn∂f(x)m=⎣⎢⎢⎢⎡∂x1∂f(x)∂x2∂f(x)...∂xn∂f(x)⎦⎥⎥⎥⎤=⎣⎢⎡∂x1∂f1(x)...∂xn∂f1(x)∂x1∂f2(x)...............∂x1∂fm(x)...∂xn∂fm(x)⎦⎥⎤n×m 但一般来说会用更加简洁的方式表达矩阵导数: x ⃗ = [ x 1 . . . x m ] , A m × n ⇒ ∂ A x ⃗ ∂ x ⃗ = A T \vec{x}=\begin{bmatrix}x_1 \\... \\x_m \end{bmatrix} \quad ,A_{m\times n} \quad \Rightarrow \frac{\partial A\vec{x} }{\partial \vec{x}} =A^T x=⎣⎡x1...xm⎦⎤,Am×n⇒∂x∂Ax=AT
当原函数存在平方形式时转换为二次型计算: ∂ x ⃗ T A x ⃗ ∂ x ⃗ = A x ⃗ + A T x ⃗ \frac{\partial \vec{x}^TA\vec{x} }{\partial \vec{x}} =A\vec{x}+A^T\vec{x} ∂x∂xTAx=Ax+ATx 值得注意,在分析系统建模的过程中A可能会得到一个对角型矩阵,此时转置等于本身。
例:线性回归中的矩阵计算
在线性回归中使用的公式主要有: ∂ A x ⃗ ∂ x ⃗ = A T \frac{\partial A\vec{x} }{\partial \vec{x}} =A^T ∂x∂Ax=AT ∂ x ⃗ T A x ⃗ ∂ x ⃗ = A x ⃗ + A T x ⃗ \frac{\partial \vec{x}^TA\vec{x} }{\partial \vec{x}} =A\vec{x}+A^T\vec{x} ∂x∂xTAx=Ax+ATx
假设有一组二维数据,x与y不相互独立,可以尝试计算得到这组数据的线性回归解。
| x | 75 | 71 | 83 | 74 | 73 | 67 | 79 | 73 | 88 | 79 | 73 | 88 | 81 | 78 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | 183 | 175 | 187 | 185 | 176 | 176 | 185 | 191 | 195 | 185 | 190 | 185 | 75 | 71 |
x是体重,y是身高。可以找到一个估计的函数来表示x-y之间的关系 y ^ = a x + b \hat{y} = ax+b y^=ax+b 基于上面概率论的部分,此时我们可以先计算所有样本数据到待估计的函数之间的距离,同时为了保证差值恒为正数便于计算,可以得到: [ y 1 − ( a x 1 + b ) ] 2 [ y 2 − ( a x 2 + b ) ] 2 . . . [ y n − ( a x n + b n ) ] 2 \begin{matrix}\left [ y_1-(ax_1+b) \right ]^2 \\\left [ y_2-(ax_2+b) \right ]^2 \\... \\\left [ y_n-(ax_n+b_n) \right ]^2 \end{matrix} [y1−(ax1+b)]2[y2−(ax2+b)]2...[yn−(axn+bn)]2 把这个差值写成一个函数的形式有: J = ∑ i = 1 n [ y i − ( a x i + b ) ] 2 J=\sum_{i=1}^{n} \left [ y_i-(ax_i+b) \right ]^2 J=i=1∑n[yi−(axi+b)]2这里的J函数就称之为代价函数,平方项的计算就是最小二乘法。通过计算J函数对a和对b的偏导数可以求出J在理论上最小的点,此时得到的a和b就是线性回归的数学最优解。
但是上面的计算过程对于计算机来所不容易编程和求解,所以可以使用线性代数的工具将其转化为矩阵计算: y ⃗ = [ y 1 , y 2 , . . . , y n ] T x ⃗ = [ x 1 x 2 . . . x n 1 1 1 1 ] T \vec{y}= [y_1, y_2, ...,y_n]^T \quad \vec{x}=\begin{bmatrix} x_1 &x_2 &... &x_n \\ 1 & 1 &1 &1 \end{bmatrix} ^T y=[y1,y2,...,yn]Tx=[x11x21...1xn1]T 此时有: y ⃗ ^ = x ⃗ × [ a b ] ⇒ J = [ y ⃗ − y ⃗ ^ ] T × [ y ⃗ − y ⃗ ^ ] \hat{\vec{y}} = \vec{x}\times \begin{bmatrix} a \\b \end{bmatrix} \Rightarrow J=[\vec{y}-\hat{\vec{y}}]^T\times [\vec{y}-\hat{\vec{y}}] y^=x×[ab]⇒J=[y−y^]T×[y−y^] ⇒ = y ⃗ T y ⃗ − 2 y ⃗ T x ⃗ θ ⃗ + θ ⃗ x ⃗ T x ⃗ θ ⃗ θ ⃗ = [ a , b ] T \Rightarrow =\vec{y}^T\vec{y}-2\vec{y}^T\vec{x}\vec{\theta}+\vec{\theta}\vec{x}^T\vec{x}\vec{\theta} \quad \vec{\theta}=[a, b]^T ⇒=yTy−2yTxθ+θxTxθθ=[a,b]T ⇒ ∂ J ∂ θ ⃗ = 0 − 2 ( y ⃗ T x ⃗ ) + 2 x ⃗ T x ⃗ θ ⃗ = 0 \Rightarrow \frac{\partial J}{\partial \vec{\theta }} =0-2(\vec{y}^T\vec{x})+2\vec{x}^T\vec{x}\vec{\theta }=0 ⇒∂θ∂J=0−2(yTx)+2xTxθ=0 ⇒ θ ⃗ = ( x ⃗ T x ⃗ ) − 1 x ⃗ T y ⃗ ⇒ θ ⃗ = [ 127.6 , 0.71 ] T \Rightarrow \vec{\theta } =(\vec{x}^T\vec{x})^{-1}\vec{x}^T\vec{y} \Rightarrow \vec{\theta }=[127.6, 0.71]^T ⇒θ=(xTx)−1xTy⇒θ=[127.6,0.71]T 至此求得了这组数据通过最小二乘法得到的解析解。那么计算如何通过迭代来模拟上面的计算过程呢?这里就十分简单了,先给定一个参数的初始值,然后计算代价函数对参数的梯度,这里上面已经推导过向量函数的导数计算,所以可以直接有梯度为: ∇ x = x ′ ⃗ × ( − y + x ⃗ × θ 0 ⃗ ) θ 0 为 初 值 , x ′ ⃗ = [ x 1 x 2 . . . x n 1 1 1 1 ] T \nabla x = \vec{x'}\times (-y+\vec{x}\times \vec{\theta_0 })\quad \theta_0为初值,\vec{x'}=\begin{bmatrix} x_1 &x_2 &... &x_n \\ 1 & 1 &1 &1 \end{bmatrix} ^T ∇x=x′×(−y+x×θ0)θ0为初值,x′=[x11x21...1xn1]T
使用matlab计算解析解
%% 使用最小二乘法计算数据的线性回归最优解clear all;
clc;x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';X =[ones(15, 1), x]; %生成x的转置扩充数据X_T = transpose(X); %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟,得到线性估计的参数a和b,这里是解析解x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r"); % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;
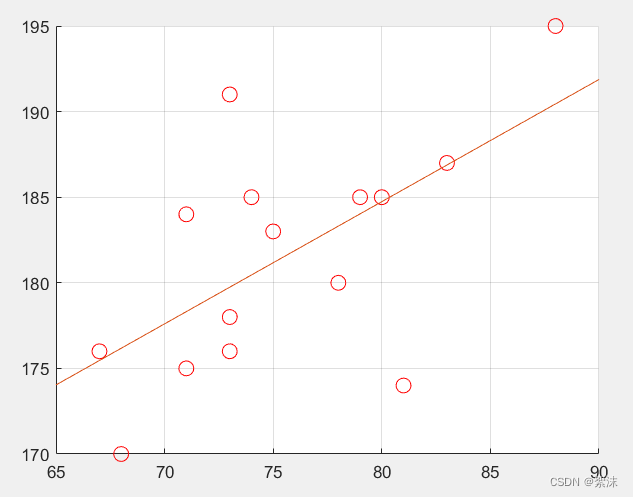
上图是最小二乘法的最优计算结果。
使用matlab通过梯度下降迭代计算解
%% 使用ML的梯度下降法迭代计算参数
clear all;
clc;x = [75, 71, 83, 74, 73, 67, 79, 73, 88, 80, 81, 78, 73, 68, 71]';
y = [183, 175, 187, 185, 176, 176, 185, 191, 195 ,185, 174, 180, 178, 170, 184]';%% 解析解
X =[ones(15, 1), x]; %生成x的转置扩充数据X_T = transpose(X); %转置
a_start = inv(X_T * X)*X_T*y; % inv计算矩阵的拟,得到线性估计的参数a和b,这里是解析解x_draw = 65:0.1:90;
scatter(X(:, 2), y, 80, "r"); % 原始数据的散点图
hold on;
plot(x_draw, a_start(2)*x_draw+a_start(1)); % 解析解的线性回归结果
grid on;%% 梯度下降回归解
% 1、定义参数,初始化矩阵% 2、while 循环 y = y - lr * x'ab_start = [100 ; 2]; % 设置一个初始值% 学习率learning_reate = 0.00002; %learning_reate = [0.001 0; 0 0.00001]; % 使用二阶学习率适应原始数据的倍率% 迭代for i = 1:100000ab_start = ab_start - learning_reate * X_T *( -y +X* ab_start); % 计算代价函数对参数矩阵的梯度,用原参数减学习率乘梯度end

此时可以看出ab_start 作为迭代计算得到的结果已经拟合于解析解算的结果了。
相关文章:

【算法小记】——机器学习中的概率论和线性代数,附线性回归matlab例程
内容包含笔者个人理解,如果错误欢迎评论私信告诉我 线性回归matlab部分参考了up主DR_CAN博士的课程 机器学习与概率论 在回归拟合数据时,根据拟合对象,可以把分类问题视为一种简答的逻辑回归。在逻辑回归中算法不去拟合一段数据而是判断输入…...
MySQL数据库的锁机制
目录 一、引言 二、锁的类型及作用 2.1 行级锁 2.2 间隙锁与临键锁 2.3 共享锁与排他锁 2.4 意向锁 2.5 表级锁 2.6 元数据锁 三、锁的管理与优化 3.1 合理设置事务隔离级别 3.2 避免长事务 3.3 索引优化 3.4 明确锁定范围 3.5 避免不必要的全表扫描 四、实战分…...
解决 conda新建虚拟环境只有一个conda-meta文件&conda新建虚拟环境不干净
像以前一样通过conda 新建虚拟环境时发现环境一团糟,首先新建虚拟环境 conda create -n newenv这时候activate newenv,通过pip list,会发现有很多很多的包,都是我在其他环境用到的。但诡异的是,来到anaconda下env的目…...

React16源码: React中的completeWork对HostText处理含更新的源码实现
HostText 1 )概述 在 completeWork 中 对 HostText的处理在第一次挂载和后续更新的不同条件下进行操作 第一次挂载主要是创建实例后续更新其实也是重新创建实例 2 )源码 定位到 packages/react-reconciler/src/ReactFiberCompleteWork.js#L663 到 c…...
网络协议与攻击模拟_07UDP协议
一、简单概念 1、UDP协议简介 UDP(用户数据报)协议,是传输层的协议。不需要建立连接,直接发送数据,不会重新排序,不需要确认。 2、UDP报文字段 源端口目的端口UDP长度UDP校验和 3、常见的UDP端口号 5…...
生命在于折腾——WeChat机器人的研究和探索
一、前言 2022年,我玩过原神,当时看到了云崽的QQ机器人,很是感兴趣,支持各种插件,查询游戏内角色相关信息,当时我也自己写了几个插件,也看到很多大佬编写的好玩的插件,后来因为QQ不…...

融资项目——EasyExcel将Excel文件保存至数据库
上一篇博客已经基本介绍了EasyExcel的配置与基本使用方法。现在准备使用EasyExcel将Excel文件保存至数据库。 1.由于我们想每读取Excel中的N条记录后将这些记录全部写入数据库中。所以首先我们在Mybatis文件内先要写一个批量保存Excel文件中的记录的sql语句。 <insert id&q…...
细粒度审计)
【Oracle】设置FGA(Fine-Grained Audit)细粒度审计
文章目录 【Oracle】设置FGA(Fine-Grained Audit)细粒度审计参考 【声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和数据库技术(ID:SQLplusDB) 收集Oracle数据库内存相关的信息 【Oracle】ORA-32017和ORA-00384错误处理 【Oracle】设…...

js vue调用activex ocx
js vue调用activex ocx 与IE调用方式不同处 CLSID和TYPE <OBJECT id"MultiplyDemo" refocx1 CLSID"{8EEF7302-1FC8-4BA0-8EA5-EC29FDBCA45B}" TYPE"application/x-itst-activex" width15% height15%></OBJECT>//调用方式1 //或是 …...
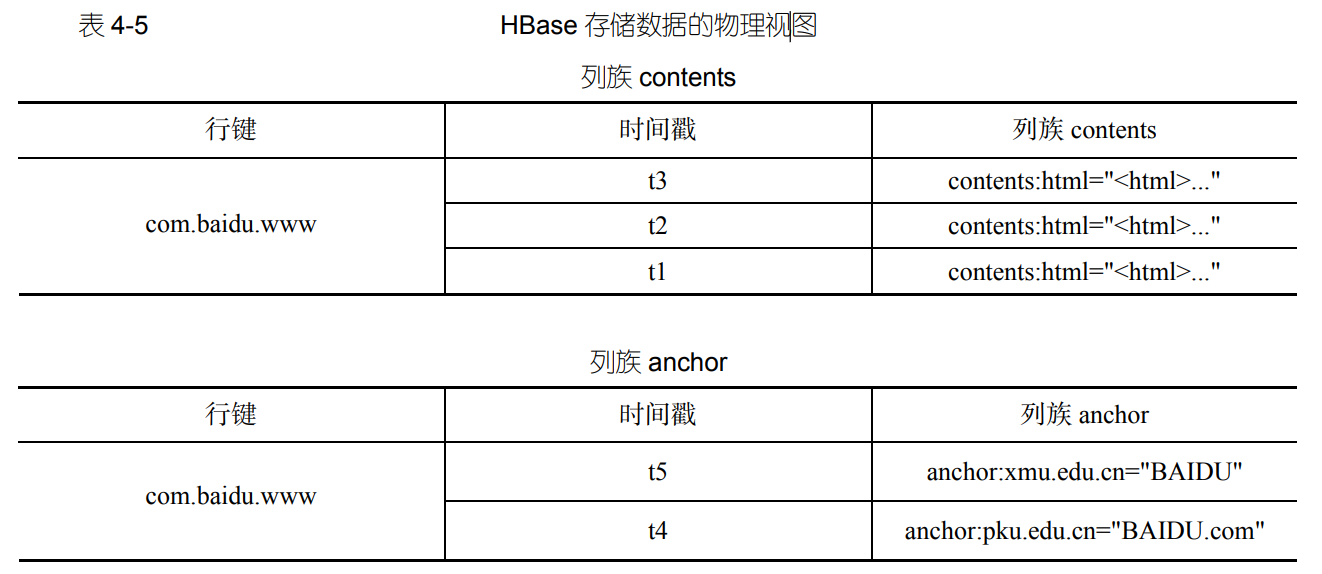
Hbas简介:数据模型和概念、物理视图
文章目录 说明零 BigTable一 Hbase简介二 HBase 访问接口简介三 行式&列式存储四 HBase 数据模型4.1 HBase 列族数据模型4.2 数据模型的相关概念4.3 数据坐标 五 概念&物理视图 说明 本文参考自林子雨老师的大数据技术原理与应用(第三版)教材内容,仅供学习…...

uniapp css样式穿透
目录 前言css样式穿透方法不加css样式穿透的代码加css样式穿透的代码不加css样式穿透的代码 与 加css样式穿透的代码 的差别参考 前言 略 css样式穿透方法 使用 /deep/ 进行css样式穿透 不加css样式穿透的代码 <style>div {background-color: #ddd;} </style>…...

【立创EDA-PCB设计基础完结】7.DRC设计规则检查+优化与丝印调整+打样与PCB生产进度跟踪
前言:本文为PCB设计基础的最后一讲,在本专栏中【立创EDA-PCB设计基础】前面已经将所有网络布线铺铜好了,接下来进行DRC设计规则检查优化与丝印调整打样与PCB生产进度跟踪 目录 1.DRC设计规则检查 2.优化与丝印调整 1.过孔连接优化 2.泪滴…...

android 线程池的管理工具类
封装了各种类型的线程池,方便直接使用 看下有哪些类型: 默认线程池,搜索模块专用线程池,网络请求专用线程池,U盘更新,同步SDK读写操作线程池,日志打印使用线程池 DEFALUT,SEARCH&…...
GNU软件编码风格(3))
编码风格之(5)GNU软件编码风格(3)
GNU软件编码标准风格(3) Author:Onceday Date: 2024年1月21日 漫漫长路,才刚刚开始… 本文主要翻译自《GNU编码标准》(GNU Coding Standards)一文。 参考文档: Linux kernel coding style — The Linux Kernel documentationGNU Coding Standard…...
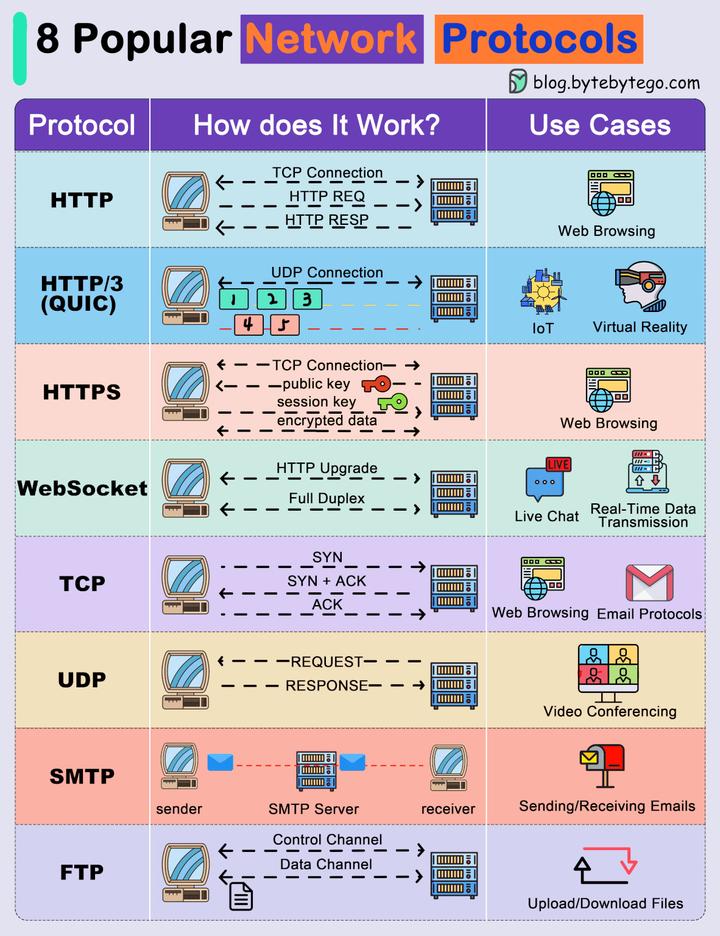
8 种网络协议
什么是网络协议? 网络协议就是计算机之间沟通的语言,为了有效地交流,计算机之间需要一种共同的规则或协议,就像我们和老外沟通之前,要先商量好用哪种语言,要么大家都说中文,要么大家都说英语&a…...
Flash读取数据库中的数据
Flash读取数据库中的数据 要读取数据库的记录,首先需要建立一个数据库,并输入一些数据。数据库建立完毕后,由Flash向ASP提交请求,ASP根据请求对数据库进行操作后将结果返回给Flash,Flash以某种方式把结果显示出来。 …...

如何写出规范优雅的代码
编码规范是成为一个优质程序员的重要一课,它是编程的样式的模板。这篇文章将介绍12中编程规范及技巧,相信学习之后你的代码一定会提升一个档次。 首先我们要明确,为什么要遵循编码规范?遵循这样的约定有什么好处? 遵循…...
【数据结构】链表(单链表与双链表实现+原理+源码)
博主介绍:✌全网粉丝喜爱、前后端领域优质创作者、本质互联网精神、坚持优质作品共享、掘金/腾讯云/阿里云等平台优质作者、擅长前后端项目开发和毕业项目实战✌有需要可以联系作者我哦! 🍅附上相关C语言版源码讲解🍅 ὄ…...
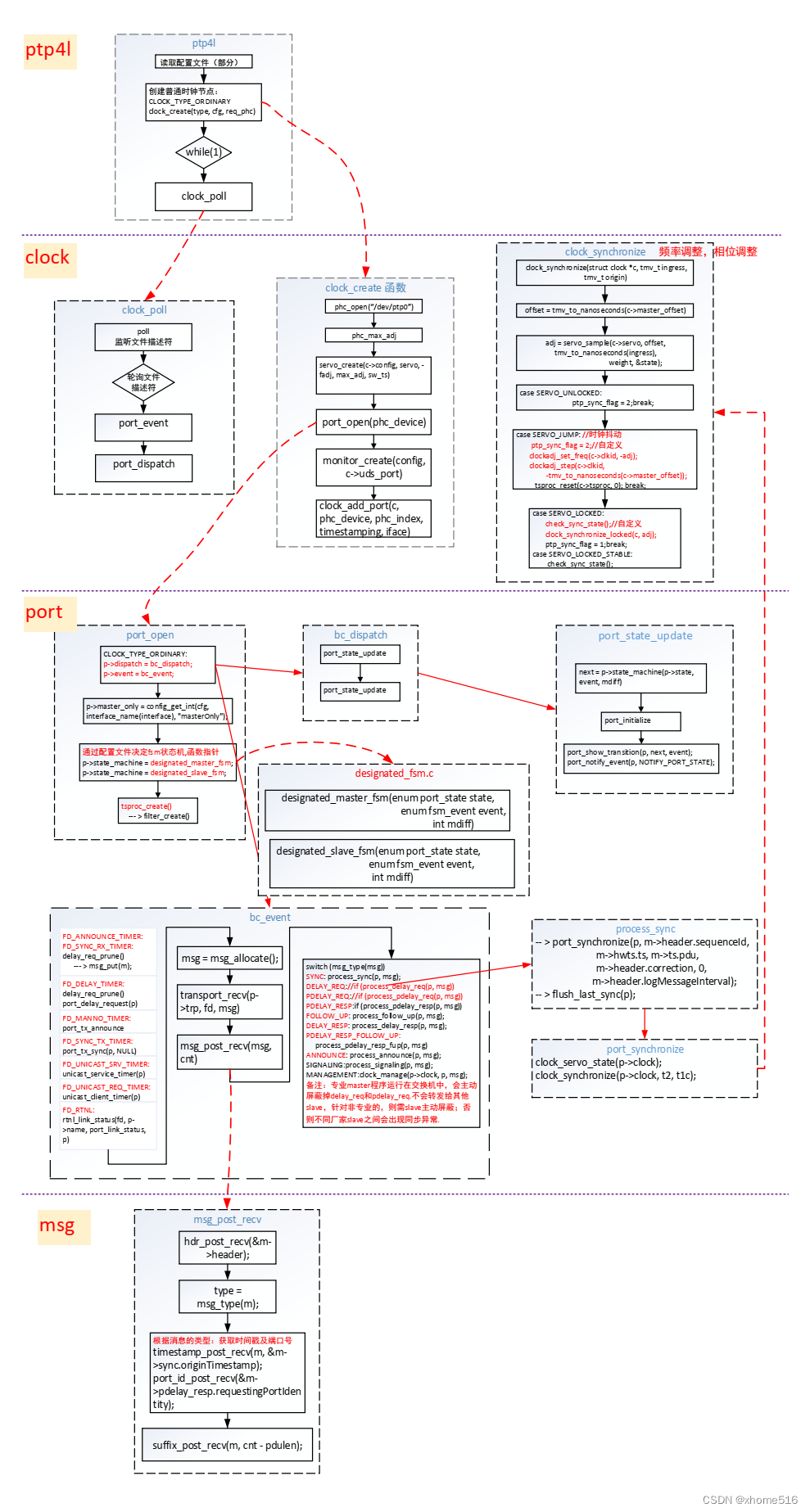
14027.ptp 控制流
文章目录 1 ptp 控制流1.1 控制流分层 1 ptp 控制流 1.1 控制流分层 大体分为4层:1 ptp4l层: 获取配置文件、创建时钟、poll监控文件描述符。2 clock时钟层:提供提供clock_poll、clock_create、clock_sync 等3 port 端口层:port…...

【昕宝爸爸小模块】深入浅出之为什么POI的SXSSFWorkbook占用内存更小
➡️博客首页 https://blog.csdn.net/Java_Yangxiaoyuan 欢迎优秀的你👍点赞、🗂️收藏、加❤️关注哦。 本文章CSDN首发,欢迎转载,要注明出处哦! 先感谢优秀的你能认真的看完本文&…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
