逆向工程:揭开科技神秘面纱的艺术

在当今这个科技飞速发展的时代,我们每天都在与各种电子产品、软件应用打交道。然而,你是否想过,这些看似复杂的高科技产品是如何被创造出来的?今天,我们就来探讨一下逆向工程这一神秘而又令人着迷的领域。
一、什么是逆向工程?
逆向工程(Reverse Engineering),顾名思义,是指通过对现有产品或系统进行拆解、分析、测量和建模等手段,以获取其设计、制造、工作原理等方面的信息,并在此基础上进行改进、优化或创新的过程。简单来说,逆向工程就是对已知事物进行深入研究,以发现其内在规律和原理,进而实现创新或改进。
二、逆向工程的应用领域
- 工业生产:在制造业中,逆向工程常被用于对已有产品进行改进和优化,提高生产效率和质量。通过对产品进行拆解、测量和分析,工程师们可以了解产品的结构、材料和工艺,从而设计出更先进、更高效的生产方案。
- 软件开发:在软件开发领域,逆向工程同样具有广泛的应用。通过对已有软件的反编译、调试和分析,开发人员可以了解软件的结构、功能和实现原理,从而进行漏洞修复、性能优化或功能扩展。
- 医学领域:在医学领域,逆向工程可以帮助医生了解疾病的发病机理和治疗方法。通过对病变组织的切片、观察和分析,医生可以深入了解疾病的病理过程,从而制定出更有效的治疗方案。
三、逆向工程的技术手段
- 三维扫描技术:通过激光、结构光或摄影等手段,对物体表面进行扫描,获取其三维形状和尺寸信息。这一技术为逆向工程提供了高效、精确的数据获取手段。
- 图像处理技术:通过对图像进行预处理、特征提取和识别等操作,实现对物体表面纹理、颜色等信息的获取。这些信息对于重建物体的三维模型具有重要意义。
- 有限元分析:通过对物体进行数学建模和计算,分析其在不同条件下的应力、应变等物理量分布,为产品优化和设计提供有力支持。
四、逆向工程的挑战与前景
尽管逆向工程在许多领域都取得了显著的成果,但我们也必须面对一些挑战。例如,知识产权保护问题、技术难度和成本等方面的限制都可能影响逆向工程的发展。然而,随着科技的进步和人们对创新需求的不断提高,逆向工程仍然具有广阔的发展前景。
未来,随着人工智能、大数据等技术的不断发展,逆向工程将更加智能化、高效化和精细化。我们可以预见,逆向工程将在更多领域发挥重要作用,推动科技进步和社会发展。
总之,逆向工程是一门充满挑战和机遇的艺术。它让我们有机会深入了解事物的内在规律和原理,为实现创新和改进提供了有力支持。在未来,我们期待看到更多关于逆向工程的精彩成果,为人类社会的发展贡献智慧和力量。
相关文章:

逆向工程:揭开科技神秘面纱的艺术
在当今这个科技飞速发展的时代,我们每天都在与各种电子产品、软件应用打交道。然而,你是否想过,这些看似复杂的高科技产品是如何被创造出来的?今天,我们就来探讨一下逆向工程这一神秘而又令人着迷的领域。 一、什么是…...
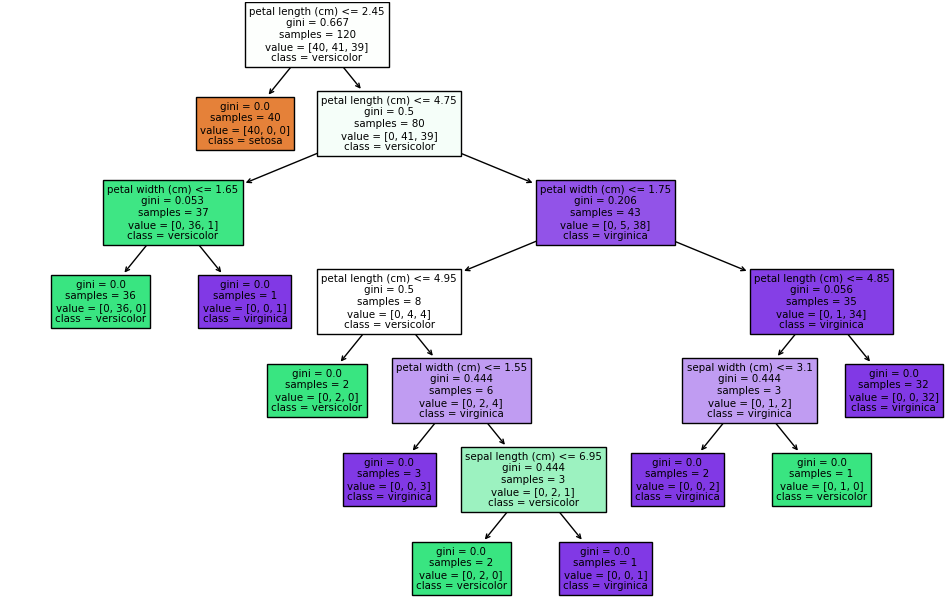
决策树的相关知识点
📕参考:ysu老师课件西瓜书 1.决策树的基本概念 【决策树】:决策树是一种描述对样本数据进行分类的树形结构模型,由节点和有向边组成。其中每个内部节点表示一个属性上的判断,每个分支代表一个判断结果的输出ÿ…...
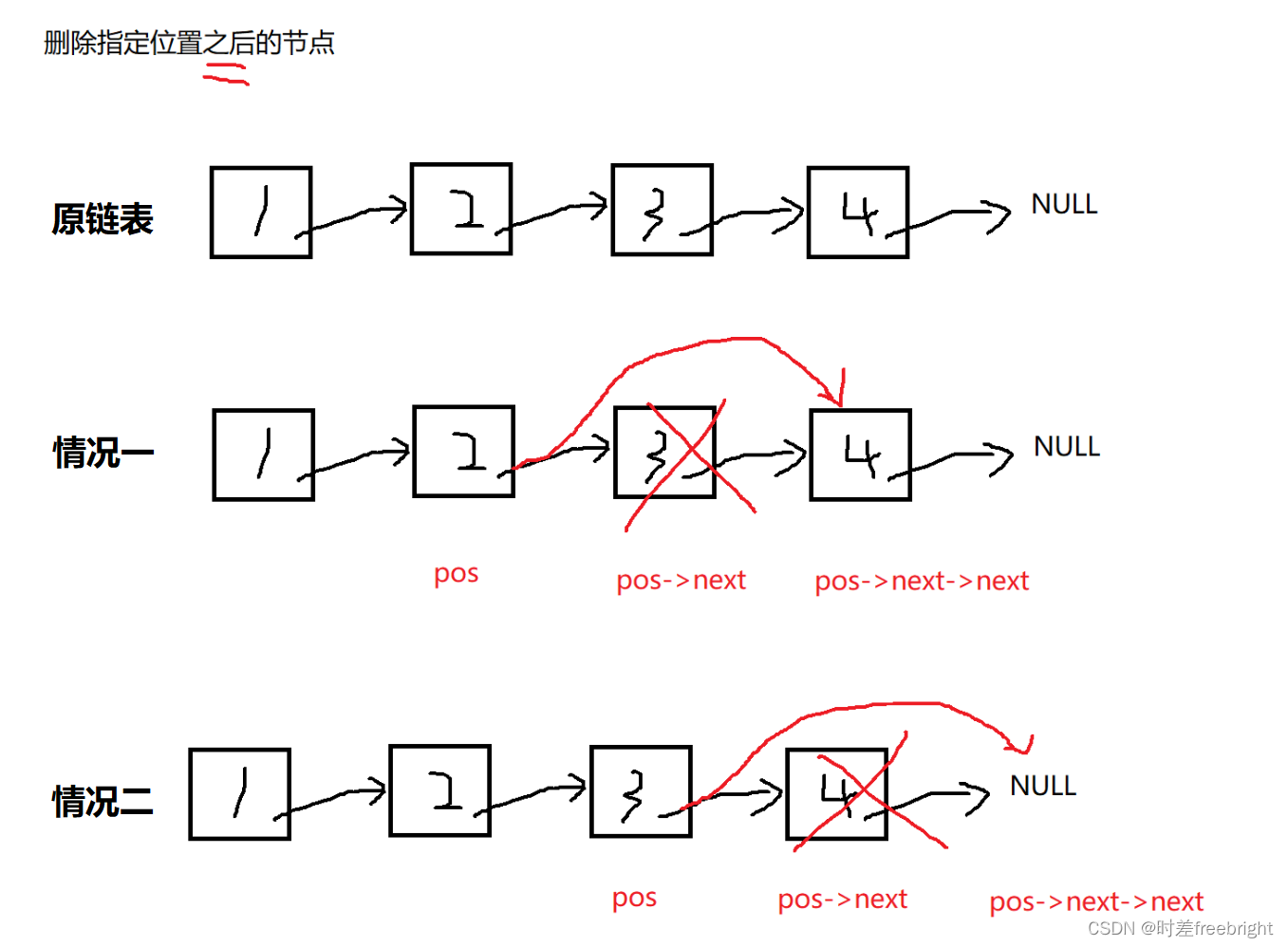
【数据结构】单向链表实现 超详细
目录 一. 单链表的实现 1.准备工作及其注意事项 1.1 先创建三个文件 1.2 注意事项:帮助高效记忆和理解 2.链表的基本功能接口 2.0 创建一个 链表 2.1 链表的打印 3.链表的创建新节点接口 4.链表的节点插入功能接口 4.1 尾插接口 4.2 头插接口 4.3 指定位…...

Opencc4j 开源中文繁简体使用介绍
Opencc4j Opencc4j 支持中文繁简体转换,考虑到词组级别。 Features 特点 严格区分「一简对多繁」和「一简对多异」。 完全兼容异体字,可以实现动态替换。 严格审校一简对多繁词条,原则为「能分则不合」。 词库和函数库完全分离,…...

vue 下载二进制文件
文章目录 概要技术细节 概要 vue 下载后端返回的二进制文件流 技术细节 import axios from "axios"; const baseUrl process.env.VUE_APP_BASE_API; //downLoadPdf("/pdf/download?pdfName" res .pdf, res); export function downLoadPdf(str, fil…...

数据结构之堆排序
对于几个元素的关键字序列{K1,K2,…,Kn},当且仅当满足下列关系时称其为堆,其中 2i 和2i1应不大于n。 { K i ≤ K 2 i 1 K i ≤ K 2 i 或 { K i ≥ K 2 i 1 K i ≥ K 2 i {\huge \{}^{K_i≤K_{2i}} _{K_i≤K_{2i1}} …...

鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之ScrollBar组件
鸿蒙(HarmonyOS)项目方舟框架(ArkUI)之ScrollBar组件 一、操作环境 操作系统: Windows 10 专业版、IDE:DevEco Studio 3.1、SDK:HarmonyOS 3.1 二、ScrollBar组件 鸿蒙(HarmonyOS)滚动条组件ScrollBar&…...
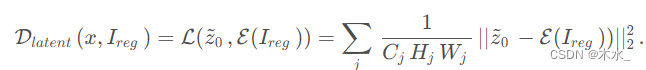
读论文:DiffBIR: Towards Blind Image Restoration with Generative Diffusion Prior
DiffBIR 发表于2023年的ICCV,是一种基于生成扩散先验的盲图像恢复模型。它通过两个阶段的处理来去除图像的退化,并细化图像的细节。DiffBIR 的优势在于提供高质量的图像恢复结果,并且具有灵活的参数设置,可以在保真度和质量之间进…...
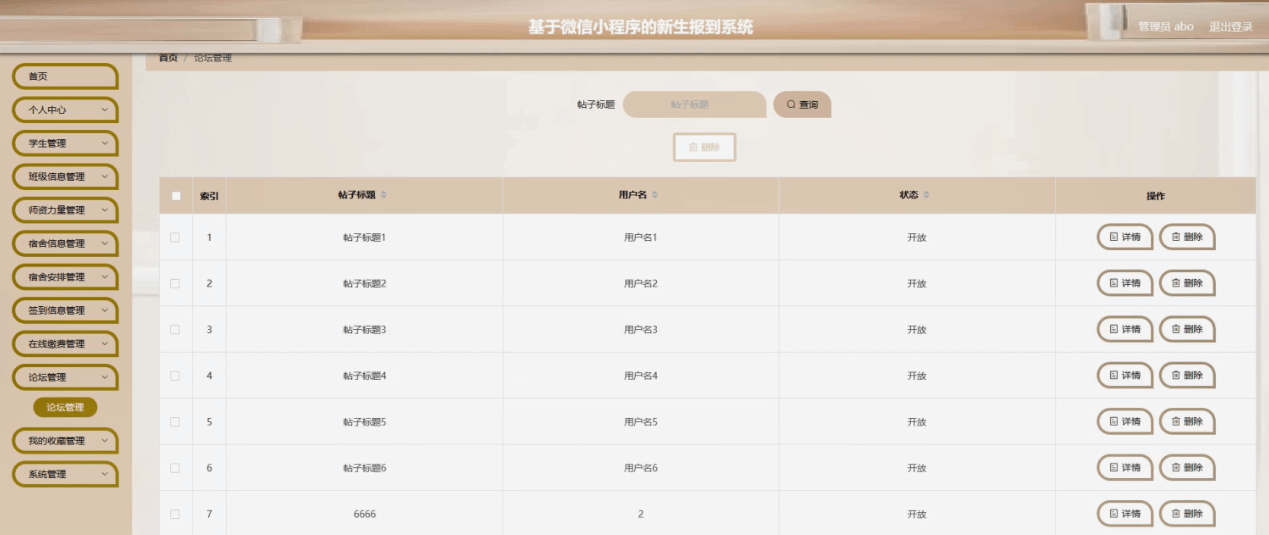
基于微信小程序的新生报到系统的研究与实现,附源码
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝12w、csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇…...
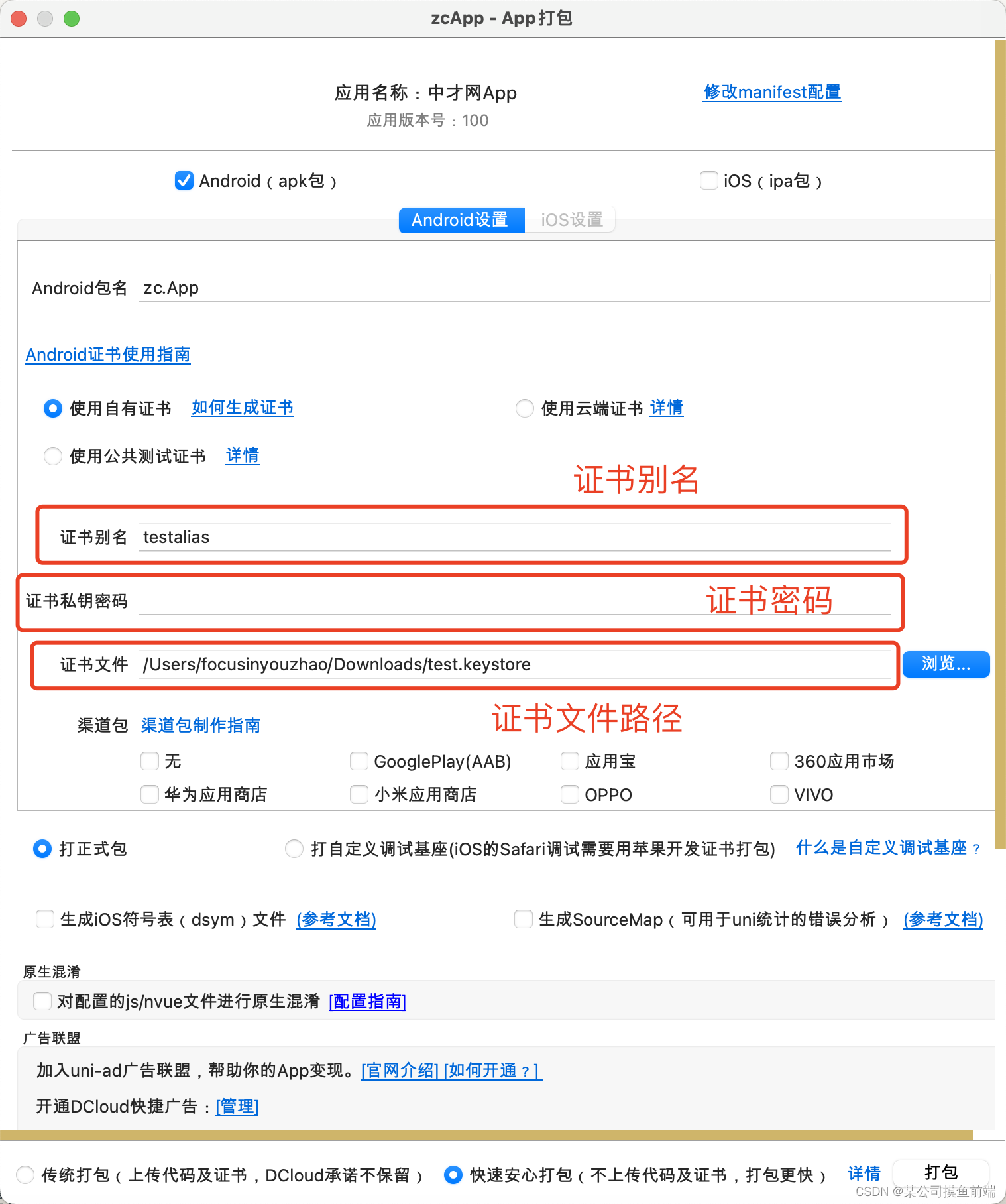
分享一下 uniapp 打包安卓apk
首先需要安装 Java 环境,这里就不做解释了 第二步:打开 mac 终端 / cmd 命令行工具 使用keytool -genkey命令生成证书 keytool -genkey -alias testalias -keyalg RSA -keysize 2048 -validity 36500 -keystore test.keystore *testalias 是证书别名&am…...
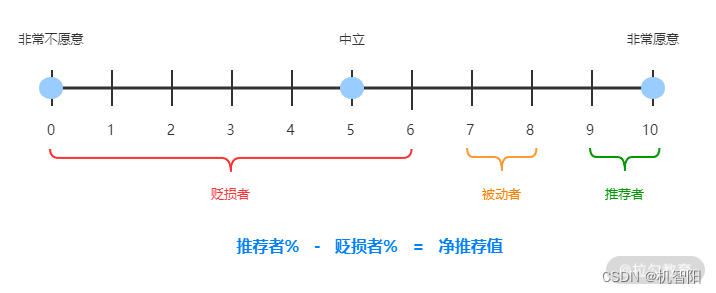
DevOps落地笔记-21|业务价值:软件发布的最终目的
上一课时介绍如何度量软件的内部质量和外部质量。在外部质量中,我们提到用户满意度是衡量软件外部质量的关键因素。“敏捷宣言”的第一条原则规定:“我们最重要的目标,是通过持续不断的及早交付有价值的软件使用户满意”。从这一点也可以看出…...

【动态规划】【前缀和】【数学】2338. 统计理想数组的数目
作者推荐 【动态规划】【前缀和】【C算法】LCP 57. 打地鼠 本文涉及知识点 动态规划汇总 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例 包括课程视频 LeetCode:2338. 统计理想数组的数目 给你两个整数 n 和 maxValue ,用于描述一个 理想…...

【已解决】onnx转换为rknn置信度大于1,图像出现乱框问题解决
前言 环境介绍: 1.编译环境 Ubuntu 18.04.5 LTS 2.RKNN版本 py3.8-rknn2-1.4.0 3.单板 迅为itop-3568开发板 一、现象 采用yolov5训练并将pt转换为onnx,再将onnx采用py3.8-rknn2-1.4.0推理转换为rknn出现置信度大于1,并且图像乱框问题…...
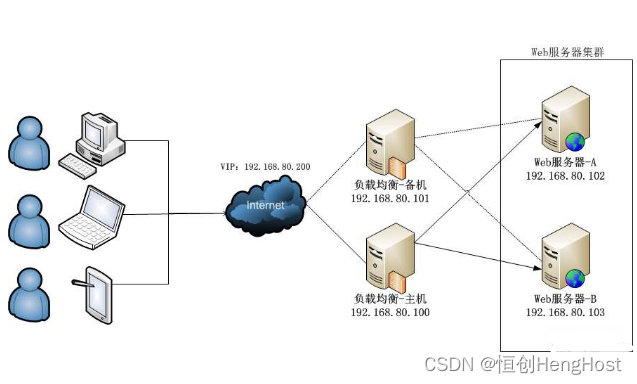
多路服务器技术如何处理大量并发请求?
在当今的互联网时代,随着用户数量的爆炸性增长和业务规模的扩大,多路服务器技术已成为处理大量并发请求的关键手段。多路服务器技术是一种并行处理技术,它可以通过多个服务器同时处理来自不同用户的请求,从而显著提高系统的整体性…...

SpringBoot - 不加 @EnableCaching 标签也一样可以在 Redis 中存储缓存?
网上文章都是说需要在 Application 上加 EnableCaching 注解才能让缓存使用 Redis,但是测试发现不用 EnableCaching 也可以使用 Redis,是网上文章有问题吗? 现在 Application 上用了 EnableAsync,SpringBootApplication࿰…...
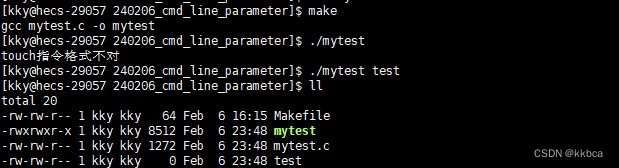
Linux------命令行参数
目录 前言 一、main函数的参数 二、命令行控制实现计算器 三、实现touch指令 前言 当我们在命令行输入 ls -al ,可以查看当前文件夹下所有文件的信息,还有其他的如rm,touch等指令,都可以帮我们完成相应的操作。 其实运行这些…...
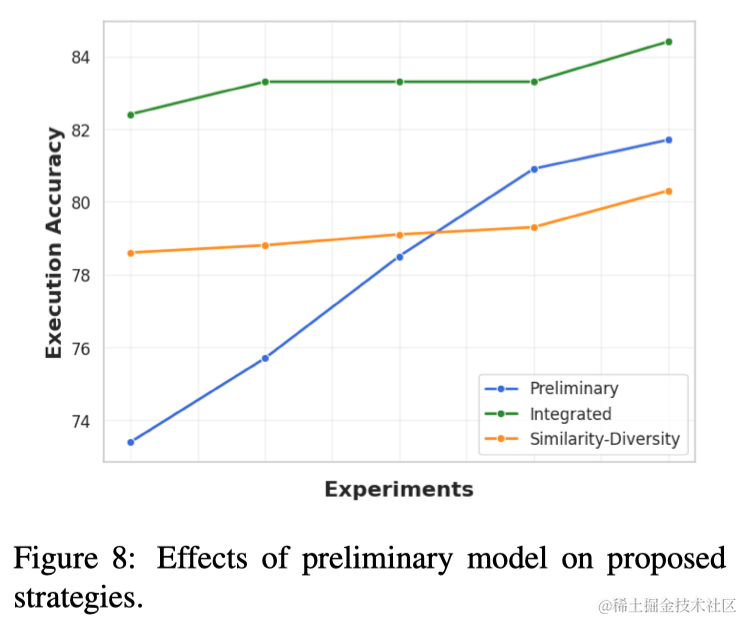
LLM少样本示例的上下文学习在Text-to-SQL任务中的探索
导语 本文探索了如何通过各种提示设计策略,来增强大型语言模型(LLMs)在Few-shot In-context Learning中的文本到SQL转换能力。通过使用示例SQL查询的句法结构来检索演示示例,并选择同时追求多样性和相似性的示例可以提高性能&…...
双非本科准备秋招(19.2)—— 设计模式之保护式暂停
一、wait & notify wait能让线程进入waiting状态,这时候就需要比较一下和sleep的区别了。 sleep vs wait 1) sleep 是 Thread 方法,而 wait 是 Object 的方法 2) sleep 不需要强制和 synchronized 配合使用,但 wait 强制和 s…...

使用SpringMVC实现功能
目录 一、计算器 1、前端页面 2、服务器处理请求 3、效果 二、用户登陆系统 1、前端页面 (1)登陆页面 (2)欢迎页面 2、前端页面发送请求--服务器处理请求 3、效果 三、留言板 1、前端页面 2、前端页面发送请求 &…...

spring aop实现接口超时处理组件
文章目录 实现思路实现代码starter组件 实现思路 这里使用FutureTask,它通过get方法以阻塞的方式获取执行结果,并设定超时时间: public V get() throws InterruptedException, ExecutionException ;public V get(long timeout, TimeUnit un…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...
