数据结构之:跳表
跳表(Skip List)是一种概率性数据结构,它通过在普通有序链表的基础上增加多级索引层来实现快速的查找、插入和删除操作。跳表的效率可以与平衡树相媲美,其操作的时间复杂度也是O(log n),但跳表的结构更简单,更易于实现。
跳表的核心特征
- 多层结构:跳表包含多个层级。最底层(第0层)包含所有的元素。每一层都是下一层的“快速通道”,每个元素出现在上层的概率通常是1/2。
- 头节点:跳表有一个头节点(head),它在所有层级中都存在。头节点的值通常不存储实际的数据,它的目的是为了搜索、插入和删除操作提供一个统一的起点。
- 随机层级:每个新插入的节点的层数是通过随机过程决定的,以确保跳表的平衡性。这意味着高层索引不会过于密集或稀疏。
数据结构组件
- 节点(SkipListNode):每个节点包含的信息有:
- 值(value):存储的数据值。
- 前进指针(forward):一个指针数组,指向同一层级的下一个节点以及上层对应的节点。
- 头节点(Head):是一个特殊的节点,它的
forward指针数组的长度等于跳表的最大层数。它在所有层级上都指向该层的第一个实际节点(如果存在)。 - 层数(Level):跳表当前的最大层数。这个值是动态的,随着新节点的插入可以增加。
操作原理
- 搜索(Search):从头节点开始,在最高层级搜索,如果当前节点的下一个节点的值小于目标值,则向前移动;如果大于目标值,则下降到下一层级继续搜索,直至找到目标值或搜索失败。
- 插入(Insert):首先通过随机过程确定新节点的层数。然后从最高层开始寻找插入位置,逐层向下直到达到新节点应存在的最低层级。在每一层,将新节点插入到适当的位置,并更新相关节点的指针。
- 删除(Delete):与搜索类似,首先定位要删除的节点。然后从其所在的最高层开始,逐层向下删除节点,并更新指针。
优点与应用
- 简单性:跳表的数据结构和算法相对简单,特别是与平衡树和B树等结构相比。
- 动态性:跳表可以很容易地支持动态数据集合的操作,如实时插入和删除。
- 效率:对于大多数操作,跳表可以提供对数时间复杂度的性能,适用于需要快速搜索操作的场景,如数据库索引和内存数据库。
跳表通过简单的随机化过程来避免复杂的重平衡操作,使得它成为一种既高效又易于实现的数据结构选项。
简单的跳表实现示例
import java.util.Random;class SkipListNode {int value;SkipListNode[] forward; // 指向不同层的指针数组public SkipListNode(int value, int level) {this.value = value;this.forward = new SkipListNode[level + 1];}
}public class SkipList {private static final float P = 0.5f;private static final int MAX_LEVEL = 16;private SkipListNode head;private int level;private Random random;public SkipList() {level = 0;head = new SkipListNode(0, MAX_LEVEL);random = new Random();}// 随机生成节点的层数private int randomLevel() {int lvl = 1;while (random.nextFloat() < P && lvl < MAX_LEVEL) {lvl++;}return lvl;}// 插入节点public void insert(int value) {int lvl = randomLevel();SkipListNode newNode = new SkipListNode(value, lvl);SkipListNode current = head;SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];for (int i = level; i >= 0; i--) {while (current.forward[i] != null && current.forward[i].value < value) {current = current.forward[i];}update[i] = current;}for (int i = 0; i <= lvl; i++) {newNode.forward[i] = update[i].forward[i];update[i].forward[i] = newNode;}if (lvl > level) {level = lvl;}}// 查找节点public boolean search(int value) {SkipListNode current = head;for (int i = level; i >= 0; i--) {while (current.forward[i] != null && current.forward[i].value < value) {current = current.forward[i];}}current = current.forward[0];return current != null && current.value == value;}// 删除节点public void delete(int value) {SkipListNode[] update = new SkipListNode[MAX_LEVEL + 1];SkipListNode current = head;for (int i = level; i >= 0; i--) {while (current.forward[i] != null && current.forward[i].value < value) {current = current.forward[i];}update[i] = current;}current = current.forward[0];if (current.value == value) {for (int i = 0; i <= level; i++) {if (update[i].forward[i] != current) break;update[i].forward[i] = current.forward[i];}while (level > 0 && head.forward[level] == null) {level--;}}}// 打印跳表的内容public void display() {System.out.println("SkipList: ");for (int i = 0; i <= level; i++) {SkipListNode node = head.forward[i];System.out.print("Level " + i + ": ");while (node != null) {System.out.print(node.value + " ");node = node.forward[i];}System.out.println();}}
}// 使用示例
public class Main {public static void main(String[] args) {SkipList list = new SkipList();list.insert(3);list.insert(6);list.insert(7);list.insert(9);list.insert(12);list.insert(19);list.insert(17);list.display();System.out.println("Searching 6: " + list.search(6));System.out.println("Searching 15: " + list.search(15));list.delete(6);System.out.println("After deleting 6: ");list.display();}
}
这段代码首先定义了SkipListNode类,它是跳表节点的结构,包括节点值和一个数组forward,数组中每个元素是对应层级的下一个节点的引用。SkipList类实现了跳表,包括初始化、插入、查找、删除和打印跳表的方法。
insert方法用于插入新的节点。search方法用于查找一个值,如果找到,则返回true。delete方法用于删除一个值。display方法用于打印跳表的所有层级和节点。
通过一个具体的例子来说明跳表的插入过程
假设我们有一个跳表,它当前的状态如下,其中每一行代表一个层级(层级0是最底层,包含所有元素):
层级3:1 --------------------------------> 9
层级2:1 ------------> 5 ------------> 9
层级1:1 ----> 3 ----> 5 ----> 7 ----> 9
层级0:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 9
现在,我们想要插入一个新的节点,值为8,并假设通过随机过程,决定新节点8将出现在层级0、1和2上(不出现在层级3上)。下面是插入过程的步骤:
步骤1:寻找每一层的插入位置
从跳表的最高层(在这个例子中是层级3)开始寻找,直到找到比插入值小的最大节点。因为8不会被插入到层级3,我们直接从层级2开始:
- 层级2:从
1开始,遍历到5,因为9大于8,所以5是层级2的插入位置。 - 层级1:同样从
1开始,遍历到5,然后到7,因为9大于8,所以7是层级1的插入位置。 - 层级0:从
1开始,按顺序遍历,直到7,因为9大于8,所以7是层级0的插入位置。
步骤2:插入节点并更新指针
- 层级2:在
5和9之间插入8,更新5的下一个指针为8,8的下一个指针为9。 - 层级1:在
7和9之间插入8,更新7的下一个指针为8,8的下一个指针为9。 - 层级0:在
7和9之间插入8,更新7的下一个指针为8,8的下一个指针为9。
插入8后,跳表变为:
层级3:1 --------------------------------> 9
层级2:1 ------------> 5 -------> 8 ----> 9
层级1:1 ----> 3 ----> 5 ----> 7 -> 8 -> 9
层级0:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9
步骤3:调整跳表的总层数(如果需要)
在这个例子中,新插入的节点8并没有增加跳表的总层数,因此不需要调整。
通过这个例子,你可以看到插入过程如何在每一层找到正确的插入位置,并更新指针来维护跳表的结构。这个过程确保了跳表的搜索效率,使得搜索、插入和删除操作的时间复杂度都为O(log n)。
相关文章:

数据结构之:跳表
跳表(Skip List)是一种概率性数据结构,它通过在普通有序链表的基础上增加多级索引层来实现快速的查找、插入和删除操作。跳表的效率可以与平衡树相媲美,其操作的时间复杂度也是O(log n),但跳表的结构更简单,…...

matlab 线性四分之一车体模型
1、内容简介 略 57-可以交流、咨询、答疑 路面采用公式积分来获得,计算了车体位移、非悬架位移、动载荷等参数 2、内容说明 略 3、仿真分析 略 线性四分之一车体模型_哔哩哔哩_bilibili 4、参考论文 略...

LeetCode第二题: 两数相加
文章目录 题目描述示例 解题思路 - 迭代法Go语言实现 - 迭代法算法分析 解题思路 - 模拟法Go语言实现 - 模拟法算法分析 解题思路 - 优化模拟法主要方法其他方法的考虑 题目描述 给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照逆序的方…...

web组态插件
插件演示地址:http://www.byzt.net 关于组态软件,首先要从组态的概念开始说起。 什么是组态 组态(Configure)的概念来自于20世纪70年代中期出现的第一代集散控制系统(Distributed Control System)…...
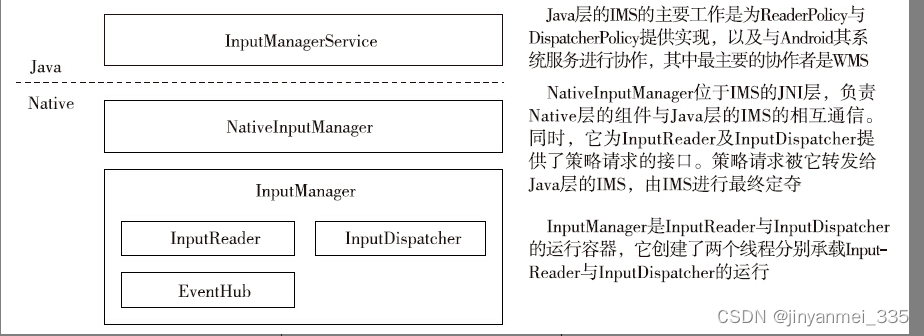
Android14 InputManager-InputManagerService环境的构造
IMS分为Java层与Native层两个部分,其启动过程是从Java部分的初始化开始,进而完成Native部分的初始化。 □创建新的IMS对象。 □调用IMS对象的start()函数完成启动 同其他系统服务一样,IMS在SystemServer中的ServerT…...

搜维尔科技:【周刊】适用于虚拟现实VR中的OptiTrack
适用于 VR 的 OptiTrack 我们通过优化对虚拟现实跟踪最重要的性能指标,打造世界上最准确、最易于使用的广域 VR 跟踪器。其结果是为任何头戴式显示器 (HMD) 或洞穴自动沉浸式环境提供超低延迟、极其流畅的跟踪。 OptiTrack 主动式 OptiTrack 世界领先的跟踪精度和…...
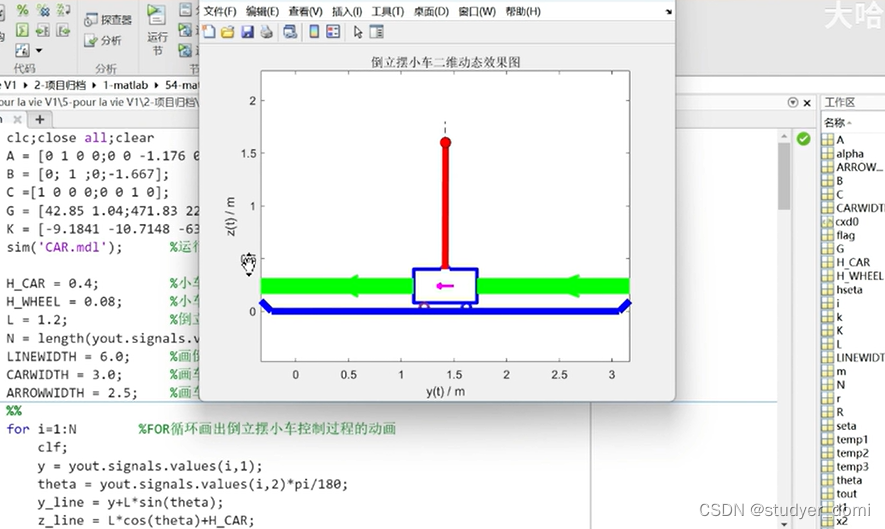
matlab倒立摆小车LQR控制动画
1、内容简介 略 54-可以交流、咨询、答疑 2、内容说明 略 摆杆长度为 L,质量为 m 的单级倒立摆(摆杆的质心在杆的中心处),小车的质量为 M。在水平方向施加控制力 u,相对参考系产生位移为 y。为了简化问题并且保其实质不变,忽…...
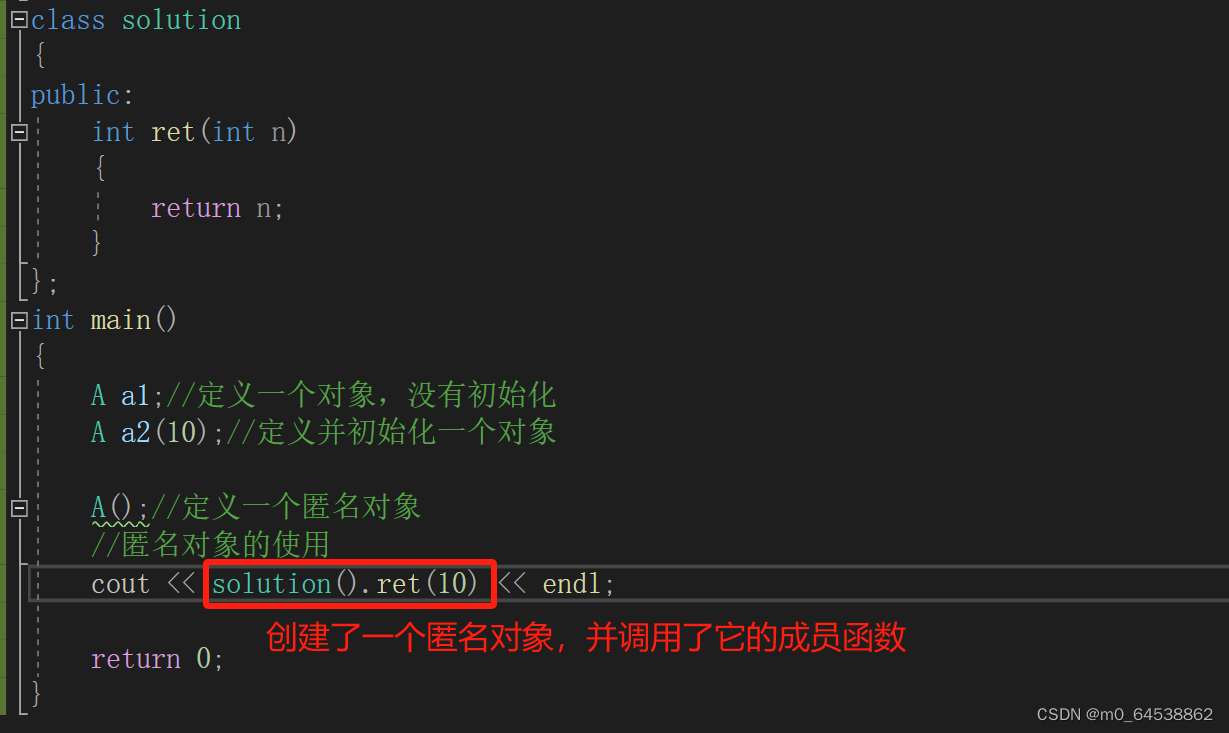
【C++】类和对象(2)
目录 1. 初始化列表 2.explicit关键字 3. Static成员 3. 友元 3.1友元函数 3.2友元类 4. 内部类 5.匿名对象 1. 初始化列表 在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值,但是这个过程并不能称为对对…...
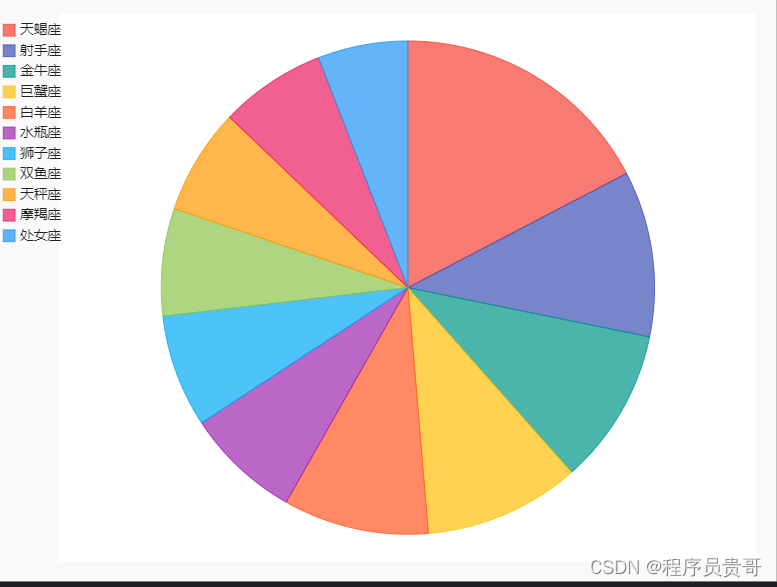
用Python实现创建十二星座数据分析图表
下面小编提供的代码中,您已经将pie.render()注释掉,并使用了pie.render_to_file(十二星座.svg)来将饼状图渲染到一个名为十二星座.svg的文件中。这是一个正确的做法,如果您想在文件中保存图表而不是在浏览器中显示它。 成功创建图表…...
备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗? 一、反转链表Ⅱ 题目描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反…...

rabbitmq知识梳理
一.WorkQueues模型 Work queues,任务模型。简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息。 当消息处理比较耗时的时候,可能生产消息的速度会远远大于消息的消费速度。长此以往,消息就会堆积越来越多,…...

【数据结构与算法】动态规划法解题20240227
动态规划法 一、什么是动态规划二、动态规划的解题步骤三、509. 斐波那契数1、动规五部曲: 四、70. 爬楼梯1、动规五部曲: 五、746. 使用最小花费爬楼梯1、动规五部曲: 一、什么是动态规划 动态规划,英文:Dynamic Pro…...
备战蓝桥杯—— 双指针技巧巧答链表2
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

半监督节点分类-graph learning
半监督节点分类相当于在一个图当中,用一部分节点的类别上已知的,有另外一部分节点的类别是未知的,目标是使用有标签的节点来推断没有标签的节点 注意 半监督节点分类属于直推式学习,直推式学习相当于出现新节点后,需要…...
软件文档-运维-开发-管理-资质-评审-招投标-验收
开发文档:这类文档主要用于记录软件的开发过程和细节,包括: 《功能要求》:描述了软件应具备的功能,是软件开发的基础。《投标方案》:向潜在的客户或招标方展示公司的技术和项目实施能力。《需求分析》&…...

猫头虎分享已解决Bug || Vue中的TypeError: Cannot read property ‘name‘ of undefined 错误
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

技术应用:使用Spring Boot、MyBatis Plus和Dynamic DataSource实现多数据源
引言 在现代的软件开发中,许多应用程序需要同时访问多个数据库。例如,一个电子商务平台可能需要访问多个数据库来存储用户信息、产品信息和订单信息等。在这种情况下,使用多数据源是一种常见的解决方案,它允许我们在一个应用程序…...
C# Onnx 使用onnxruntime部署实时视频帧插值
目录 介绍 效果 模型信息 项目 代码 下载 C# Onnx 使用onnxruntime部署实时视频帧插值 介绍 github地址:https://github.com/google-research/frame-interpolation FILM: Frame Interpolation for Large Motion, In ECCV 2022. The official Tensorflow 2…...

编程笔记 Golang基础 016 数据类型:数字类型
编程笔记 Golang基础 016 数据类型:数字类型 1. 整数类型(Integer Types)a) 固定长度整数:b) 变长整数: 2. 浮点数类型(Floating-Point Types)3. 复数类型(Complex Number Types&…...
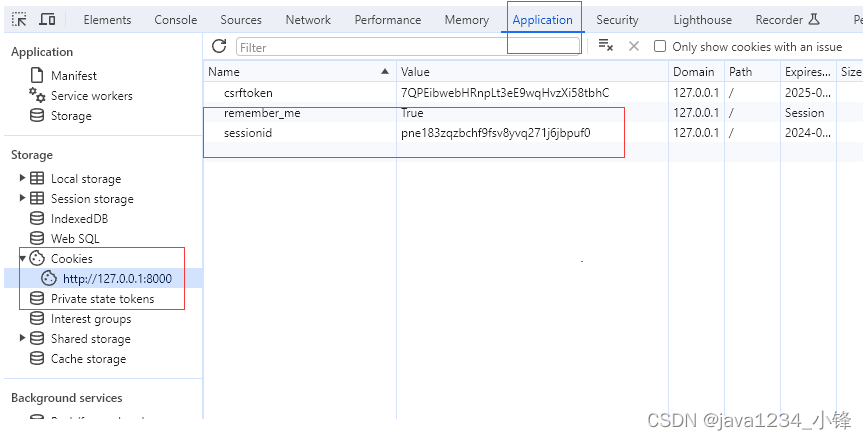
一周学会Django5 Python Web开发-会话管理(CookiesSession)
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计26条视频,包括:2024版 Django5 Python we…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...
