数学建模【相关性模型】
一、相关性模型简介
相关性模型并不是指一个具体的模型,而是一类模型,这一类模型用来判断变量之间是否具有相关性。一般来说,分析两个变量之间是否具有相关性,我们根据数据服从的分布和数据所具有的特点选择使用pearson(皮尔逊)相关系数和spearman(斯皮尔曼)等级相关系数;分析两组变量,每组变量都有多个指标的时候,无论是pearson相关系数还是spearman等级相关系数都无能为力,所以又要介绍一个新的典型相关分析来解决这个问题。
二、适用赛题
显而易见,这些相关性模型适用于探究变量之间的关系,帮助了解它们是否存在相关性,以及相关性的强度和方向。
三、模型流程
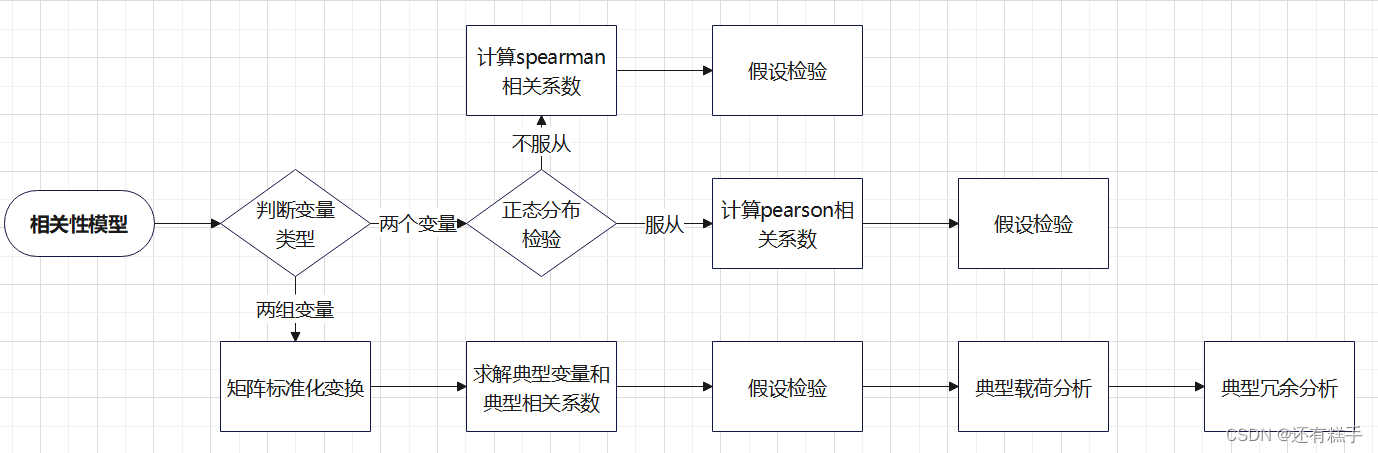
四、流程分析
因为整个流程包含三个模型,所以会以pearson相关系数,spearman等级相关系数,典型相关分析的顺序来讲解。
注:本篇存在大量的概率论与数理统计的知识,这里并不对其中出现的知识、定理等作概念说明和详细证明
1.pearson相关系数
可以从流程图看到,应用pearson相关系数条件还是比较苛刻的。首先得是两个变量之间,其次这两个变量的数据还要服从正态分布。其实应用pearson相关系数的条件还不止,后面会全部介绍。
①正态分布检验
为什么要正态分布检验?
- 第一,实验数据通常假设是成对的来自于正态分布的总体。因为我们在求pearson相关系数以后,通常还会用t检验之类的方法来进行皮尔逊相关系数检验,而t检验是基于数据呈正态分布的假设的
- 第二,实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大
- 第三,每组样本之间是独立抽样的。构造t统计量时需要用到
Ⅰ正态分布JB检验(大样本 n > 30)
雅克-贝拉检验(Jarque-Bera test)

这是原理,但是在MATLAB中,代码很简单
注:有些地方正态分布峰度为0,MATLAB中是3
skewness(x) % 偏度
kurtosis(x) % 峰度可以用这两句查询数据的偏度和峰度
MATLAB中进行JB检验的语法:
[h, p] = jbtest(x, alpha);当输出h等于1时,表示拒绝原假设;h等于0则代表不能拒绝原假设。alpha就是显著性水平,一般取0.05, 此时置信水平为1 - 0.05 = 0.95。x就是我们要检验的随机变量,注意这里的x只能是向量。
ⅡShapiro-wilk检验(小样本 3 ≤ n ≤ 50)
Shapiro-wilk 夏皮洛-威尔克检验

此操作一般在SPSS软件上进行。
②计算相关系数
pearson相关系数的原理在概率论课本上有,无论是总体还是样本。这里给出MATLAB中如何求
R = corrcoef(A) % 返回A的相关系数的矩阵,其中A的列表示随机变量(指标),行表示观测值(样本)
R = corrcoef(A, B) % 返回两个随机变量A和B (两个向量) 之间的系数关于pearson相关系数的总结
- 如果两个变量本身就是线性的关系,那么pearson相关系数绝对值大的就是相关性强,小的就是相关性弱
- 在不确定两个变量是什么关系的情况下,即使算出pearson相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说它们相关,我们一定要画出散点图来看才行
③假设检验
事实上,比起相关系数的大小,我们往往更关注的是显著性(假设检验)
原理这里不再给出,证明过于复杂。
这里用更好的方法:p值判断法
一行代码得到p值
[R, P] = corrcoef(test);R返回的是相关系数表,P返回的是对应于每个相关系数的p值

注:拒绝原假设意味着pearson相关系数显著的异于0
2.spearman等级相关系数
pearson相关系数不能用,就使用spearman等级相关系数。鉴于pearson相关系数中已经介绍过正态分布检验,这里不在重复。
①计算相关系数

注:如果有的数值相同,则将它们所在的位置取算术平均。
举个例子:
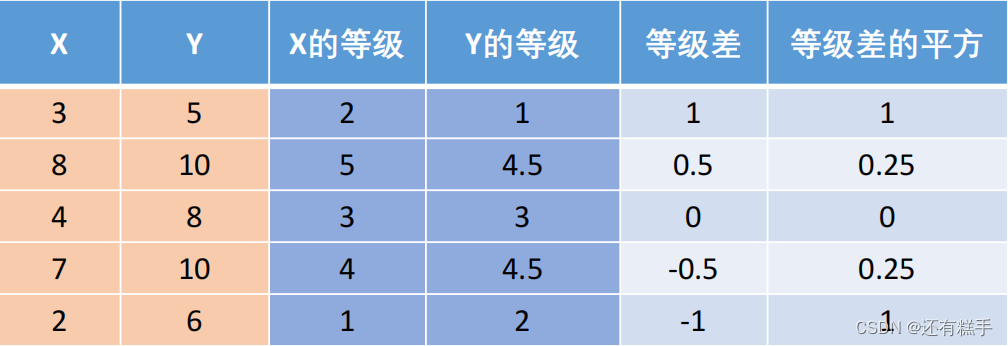
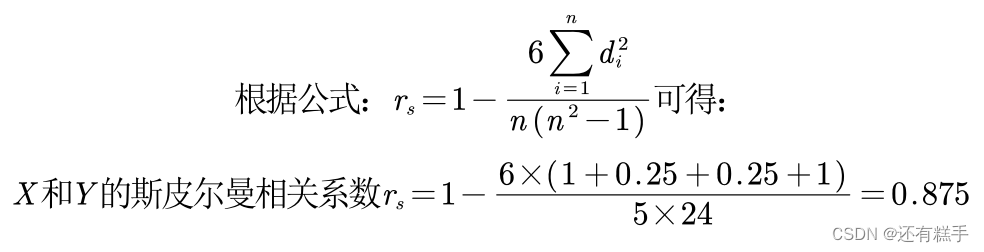
在MATLAB中,代码也是很简单
coeff = corr(X, Y, 'type', 'Spearman'); % 这里的X和Y必须是列向量
coeff = corr(x, 'type', 'Spearman'); % 这时计算X矩阵各列之间的spearman相关系数②假设检验
Ⅰ小样本情况(n ≤ 30)
直接查临界值表即可
|
| 单尾检验的显著水平 | |||
| .05 | .025 | .01 | .005 | |
| 双尾检验的显著水平 | ||||
| .10 | .05 | .02 | .01 | |
| 4 | 1.000 | |||
| 5 | 0.900 | 1.000 | 1.000 | |
| 6 | 0.829 | 0.886 | 0.943 | 1.000 |
| 7 | 0.714 | 0.786 | 0.893 | 0.929 |
| 8 | 0.643 | 0.738 | 0.833 | 0.881 |
| 9 | 0.600 | 0.700 | 0.783 | 0.833 |
| 10 | 0.564 | 0.648 | 0.745 | 0.794 |
| 11 | 0.536 | 0.618 | 0.709 | 0.755 |
| 12 | 0.503 | 0.587 | 0.671 | 0.727 |
| 13 | 0.484 | 0.560 | 0.648 | 0.703 |
| 14 | 0.464 | 0.538 | 0.622 | 0.675 |
| 15 | 0.443 | 0.521 | 0.604 | 0.654 |
| 16 | 0.429 | 0.503 | 0.582 | 0.635 |
| 17 | 0.414 | 0.485 | 0.566 | 0.615 |
| 18 | 0.401 | 0.472 | 0.550 | 0.600 |
| 19 | 0.391 | 0.460 | 0.535 | 0.584 |
| 20 | 0.380 | 0.447 | 0.520 | 0.570 |
| 21 | 0.370 | 0.435 | 0.508 | 0.556 |
| 22 | 0.361 | 0.425 | 0.496 | 0.544 |
| 23 | 0.353 | 0.415 | 0.486 | 0.532 |
| 24 | 0.344 | 0.406 | 0.476 | 0.521 |
| 25 | 0.337 | 0.398 | 0.466 | 0.511 |
| 26 | 0.331 | 0.390 | 0.457 | 0.501 |
| 27 | 0.324 | 0.382 | 0.448 | 0.491 |
| 28 | 0.317 | 0.375 | 0.440 | 0.483 |
| 29 | 0.312 | 0.368 | 0.433 | 0.475 |
| 30 | 0.306 | 0.362 | 0.425 | 0.467 |
| 35 | 0.283 | 0.335 | 0.394 | 0.433 |
| 40 | 0.264 | 0.313 | 0.368 | 0.405 |
| 45 | 0.248 | 0.294 | 0.347 | 0.382 |
| 50 | 0.235 | 0.279 | 0.329 | 0.363 |
| 60 | 0.214 | 0.255 | 0.300 | 0.331 |
| 70 | 0.190 | 0.235 | 0.278 | 0.307 |
| 80 | 0.185 | 0.220 | 0.260 | 0.287 |
| 90 | 0.174 | 0.207 | 0.245 | 0.271 |
| 100 | 0.165 | 0.197 | 0.233 | 0.257 |
注:样本相关系数r必须大于等于表中的临界值,才能得出显著的结论。
Ⅱ大样本情况
依旧是选择更好用的p值检验法
[R, P] = corr(test, 'type', 'Spearman'); % 直接给出相关系数和p值这里和p值和pearson相关系数假设检验那里的p值解释相同。
3.pearson相关系数和spearman等级相关系数选择
- 连续数据,正态分布,线性关系,用pearson相关系数是最恰当,当然用spearman等级相关系数也可以,就是效率没有pearson相关系数高
- 上述任一条件不满足,就用spearman等级相关系数,不能用pearson相关系数
- 两个定序数据之间也用spearman等级相关系数,不能用pearson相关系数
定序数据是指仅仅反映观测对象等级、顺序关系的数据,是由定序尺度计量形成的,表现为类别,可以进行排序,属于品质数据。
例如:优、良、差;我们可以用1表示差、2表示良、3表示优,但请注意,用2除以1得出的2并不代表任何含义。定序数据最重要的意义代表了- -组数据中的某种逻辑顺序。
注:斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广,只要数据满足单调关系(例如线性函数、指数函数、对数函数等)就能够使用。
4.典型相关分析
声明:对于典型相关分析,其中原理、证明过于复杂,本篇不作涉及,只介绍得出结果的流程。
基本思想
典型相关分析由Hotelling提出,其基本思想和主成分分析非常相似。首先在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。然后选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此继续下去,直到两组变量之间的相关性被提取完毕为此。被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。
①矩阵标准化变换
矩阵的标准化变换属于线性代数的知识,这里介绍为什么要对矩阵进行标准化变化的操作
- 典型相关分析涉及多个变量,不同的变量往往具有不同的量纲及不同的数量级别。在进行典型相关分析时,由于典型变量是原始变量的线性组合,具有不同量纲变量的线性组合显然失去了实际意义
- 其次,不同的数量级别会导致“以大吃小”,即数量级别小的变量的影响会被忽略,从而影响了分析结果的合理性
- 因此,为了消除量纲和数量级别的影响,必须对数据先做标准化变换处理,然后再做典型相关分析
②求解
再看过第一步之后肯定是一头雾水,矩阵是哪里来的?这里对典型相关分析中的变量做一些介绍

规定有
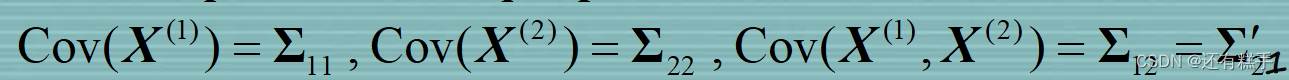
第一步的矩阵标准化就是对这四个矩阵进行操作
这里以一组数据为例子
康复俱乐部对20名中年人测量了三个生理指标:体重(x1),腰围(x2),脉搏(x3);三个训练指标:引体向上次数(y1),起坐次数(y2),跳跃次数(y3)。分析生理指标与训练指标的相关性。
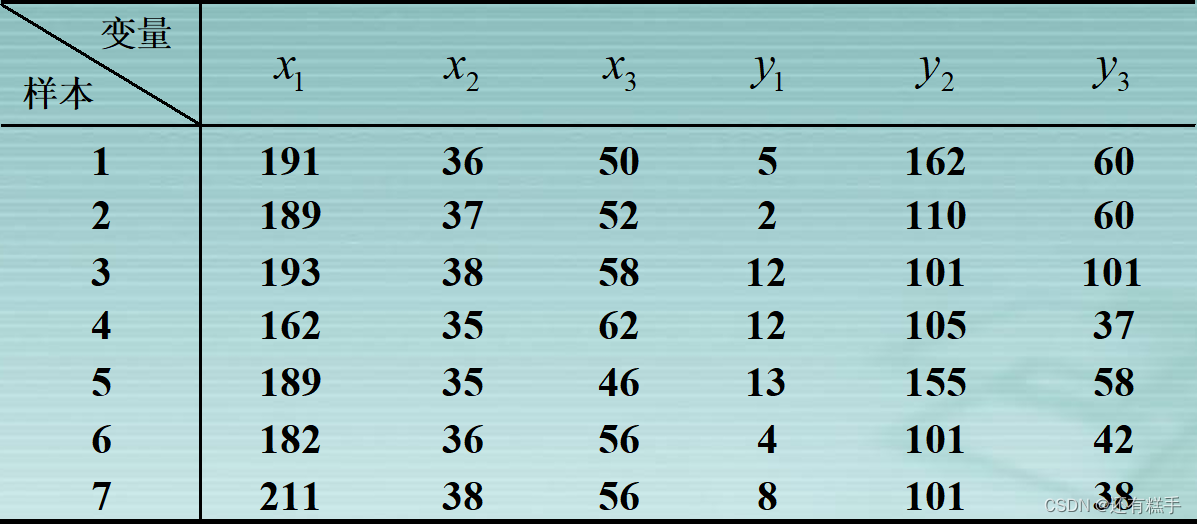
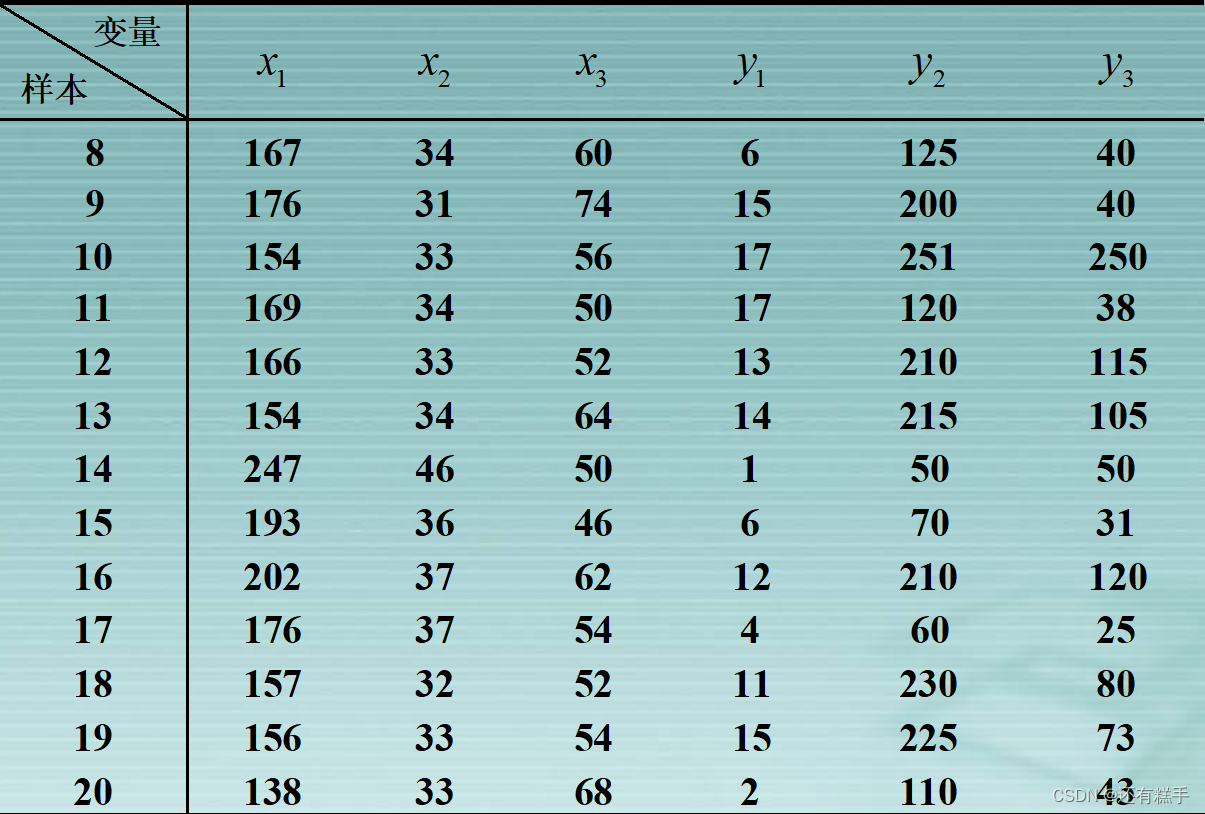
根据数据可得
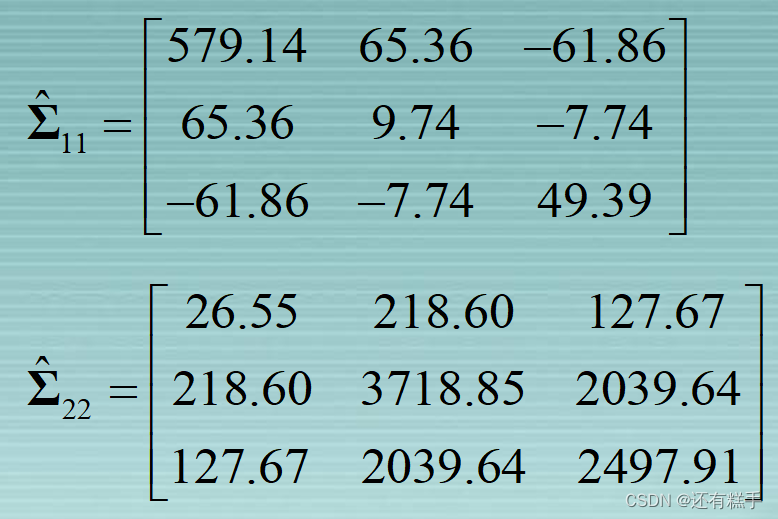
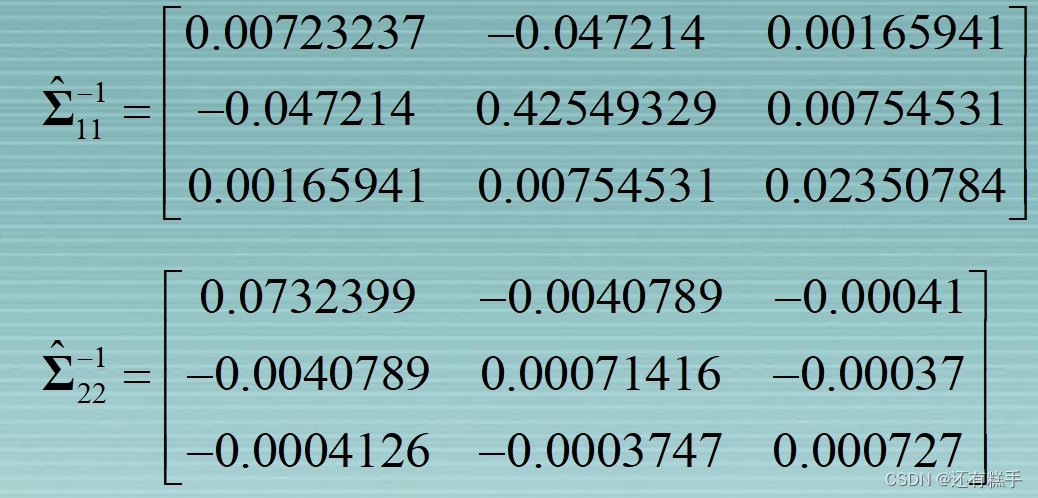
在标准化之后,矩阵用R表示

设置A和B
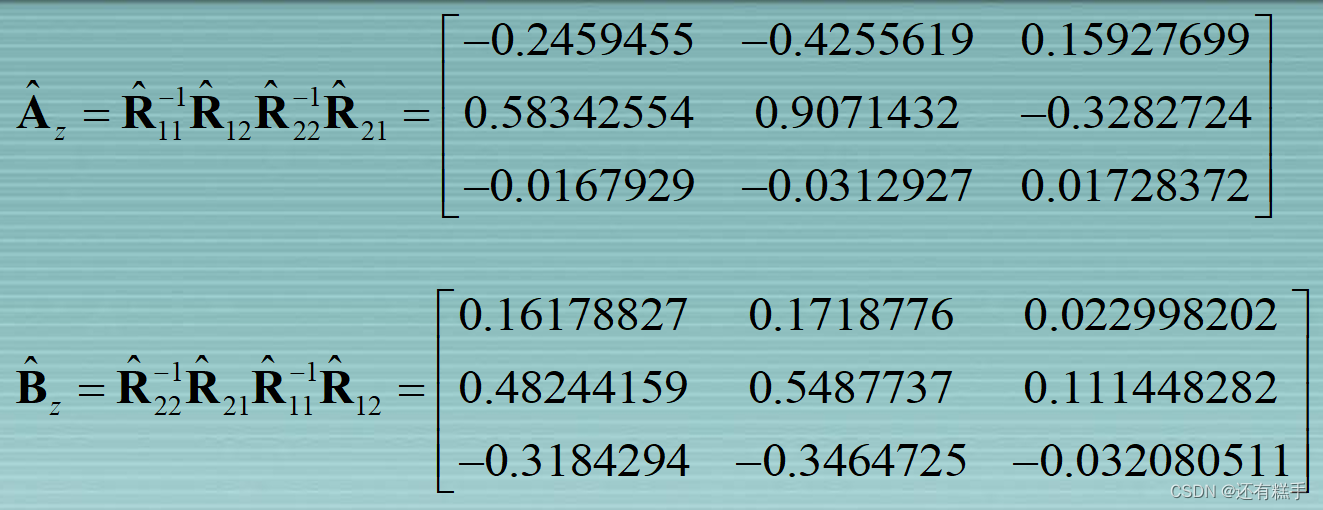
这里A和B的特征值是相同的

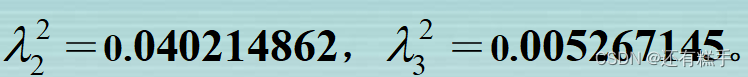
则可得

每一个a和b都是对应的特征向量,在这里也就是典型相关系数

第二对和第三对也是如此。
③假设检验
对于每一对典型变量进行计算




④典型载荷分析
进行典型载荷分析有助于更好解释分析已提取的p对典型变量。所谓的典型载荷分析是指原始变量与典型变量之间相关性分析。

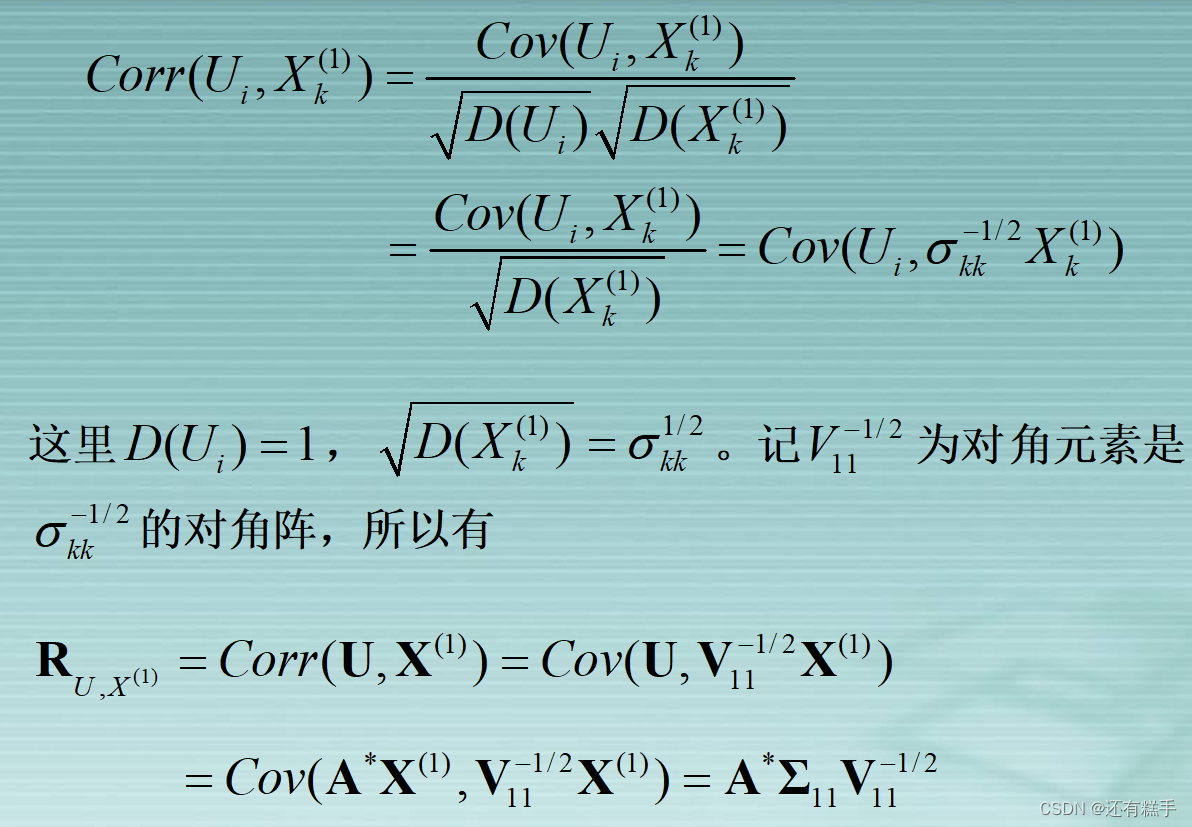

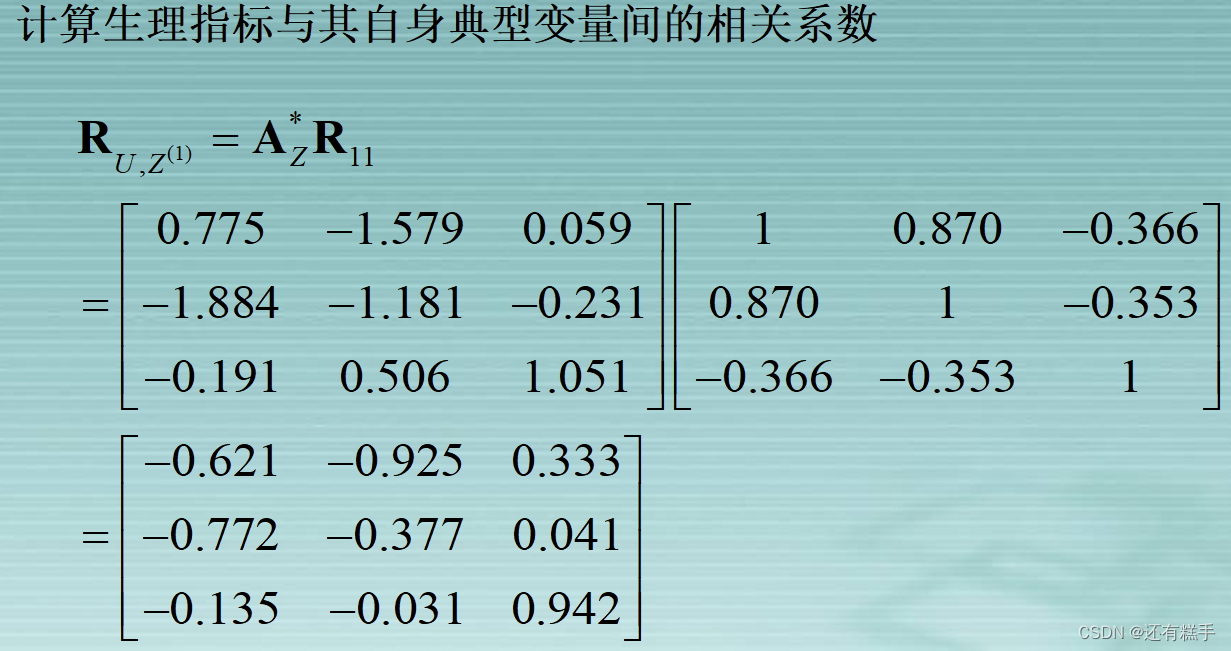

⑤典型冗余分析




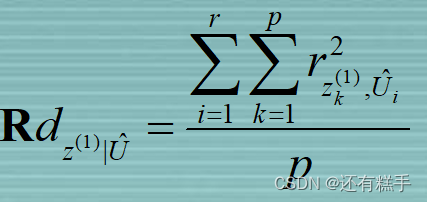


5.补充
可以看见,典型相关分析过于复杂,不过可以利用SPSS软件完成对数据相关性的分析,包括pearson相关系数和spearman等级相关系数。
相关文章:

数学建模【相关性模型】
一、相关性模型简介 相关性模型并不是指一个具体的模型,而是一类模型,这一类模型用来判断变量之间是否具有相关性。一般来说,分析两个变量之间是否具有相关性,我们根据数据服从的分布和数据所具有的特点选择使用pearsonÿ…...

「优选算法刷题」:字母异位词分组
一、题目 给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。 字母异位词 是由重新排列源单词的所有字母得到的一个新单词。 示例 1: 输入: strs ["eat", "tea", "tan", "ate", "na…...

【教程】 iOS混淆加固原理篇
目录 摘要 引言 正文 1. 加固的缘由 2. 编译过程 3. 加固类型 1) 字符串混淆 2) 类名、方法名混淆 3) 程序结构混淆加密 4) 反调试、反注入等一些主动保护策略 4. 逆向工具 5. OLLVM 6. IPA guard 7. 代码虚拟化 总结 摘要 本文介绍了iOS应用程序混淆加固的缘由…...

《银幕上的编码传奇:计算机科学与科技精神的光影盛宴》
目录 1.在电影的世界里,计算机科学不仅是一门严谨的学科,更是一种富有戏剧张力和人文思考的艺术载体。 2.电影作为现代文化的重要载体,常常以其丰富的想象力和视觉表现力来探讨计算机科学和技术的各种前沿主题。 3.电影中的程序员角色往往…...
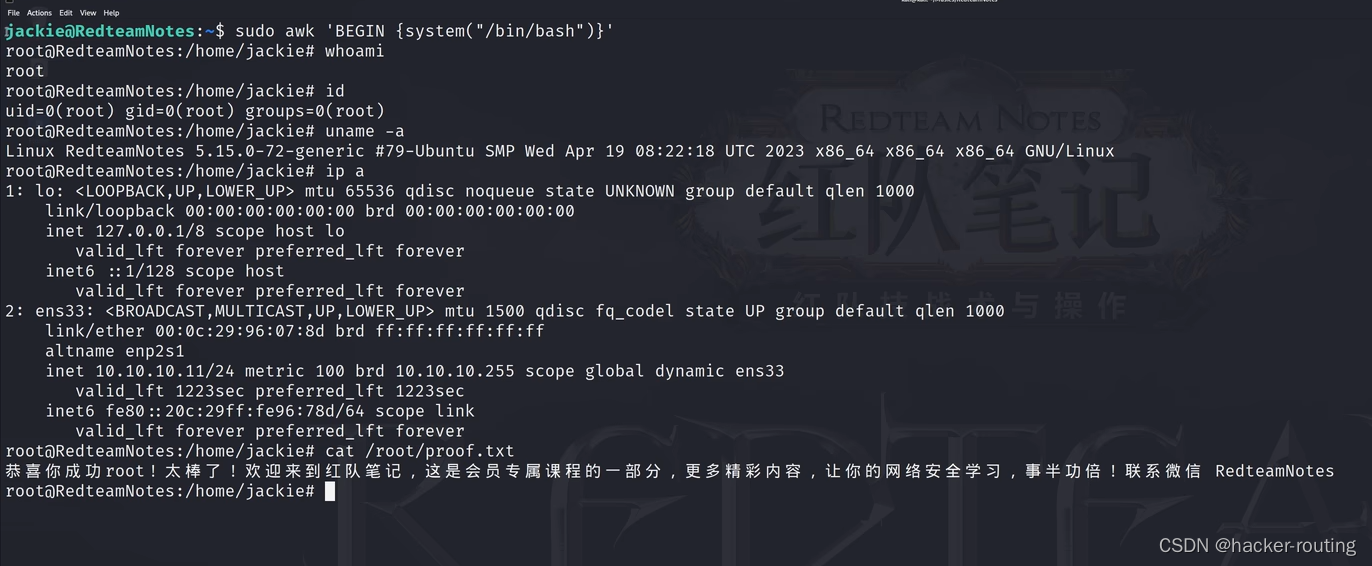
linux提权之sudo风暴
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【Java】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏 …...

数据结构之:跳表
跳表(Skip List)是一种概率性数据结构,它通过在普通有序链表的基础上增加多级索引层来实现快速的查找、插入和删除操作。跳表的效率可以与平衡树相媲美,其操作的时间复杂度也是O(log n),但跳表的结构更简单,…...

matlab 线性四分之一车体模型
1、内容简介 略 57-可以交流、咨询、答疑 路面采用公式积分来获得,计算了车体位移、非悬架位移、动载荷等参数 2、内容说明 略 3、仿真分析 略 线性四分之一车体模型_哔哩哔哩_bilibili 4、参考论文 略...

LeetCode第二题: 两数相加
文章目录 题目描述示例 解题思路 - 迭代法Go语言实现 - 迭代法算法分析 解题思路 - 模拟法Go语言实现 - 模拟法算法分析 解题思路 - 优化模拟法主要方法其他方法的考虑 题目描述 给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照逆序的方…...

web组态插件
插件演示地址:http://www.byzt.net 关于组态软件,首先要从组态的概念开始说起。 什么是组态 组态(Configure)的概念来自于20世纪70年代中期出现的第一代集散控制系统(Distributed Control System)…...
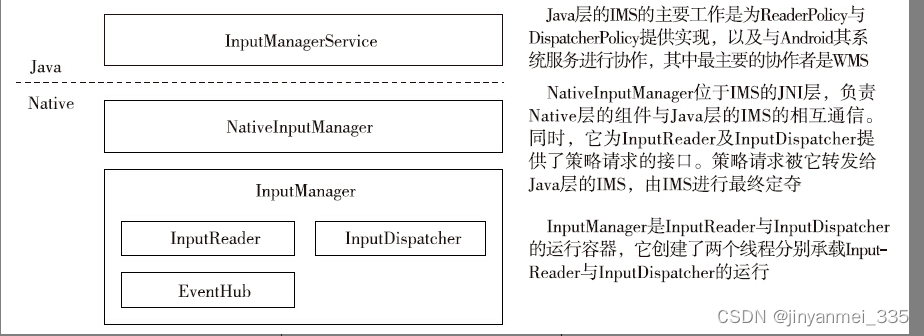
Android14 InputManager-InputManagerService环境的构造
IMS分为Java层与Native层两个部分,其启动过程是从Java部分的初始化开始,进而完成Native部分的初始化。 □创建新的IMS对象。 □调用IMS对象的start()函数完成启动 同其他系统服务一样,IMS在SystemServer中的ServerT…...

搜维尔科技:【周刊】适用于虚拟现实VR中的OptiTrack
适用于 VR 的 OptiTrack 我们通过优化对虚拟现实跟踪最重要的性能指标,打造世界上最准确、最易于使用的广域 VR 跟踪器。其结果是为任何头戴式显示器 (HMD) 或洞穴自动沉浸式环境提供超低延迟、极其流畅的跟踪。 OptiTrack 主动式 OptiTrack 世界领先的跟踪精度和…...
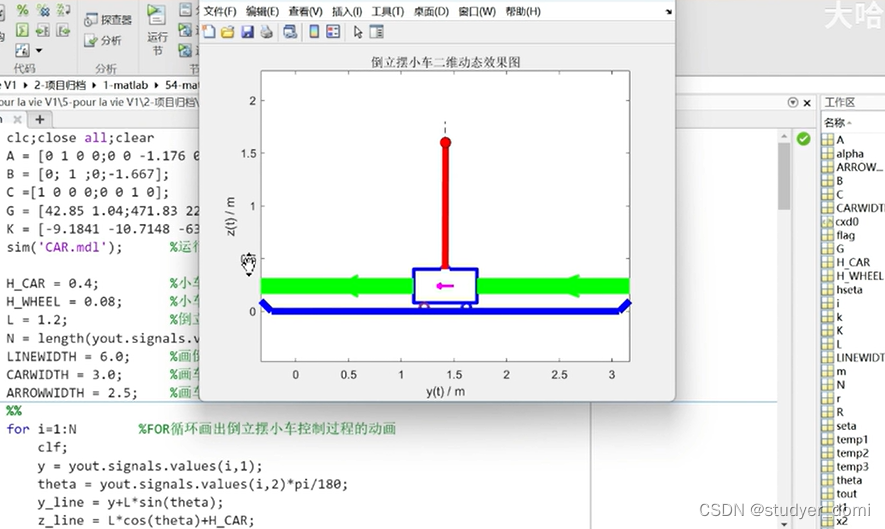
matlab倒立摆小车LQR控制动画
1、内容简介 略 54-可以交流、咨询、答疑 2、内容说明 略 摆杆长度为 L,质量为 m 的单级倒立摆(摆杆的质心在杆的中心处),小车的质量为 M。在水平方向施加控制力 u,相对参考系产生位移为 y。为了简化问题并且保其实质不变,忽…...
【C++】类和对象(2)
目录 1. 初始化列表 2.explicit关键字 3. Static成员 3. 友元 3.1友元函数 3.2友元类 4. 内部类 5.匿名对象 1. 初始化列表 在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值,但是这个过程并不能称为对对…...
用Python实现创建十二星座数据分析图表
下面小编提供的代码中,您已经将pie.render()注释掉,并使用了pie.render_to_file(十二星座.svg)来将饼状图渲染到一个名为十二星座.svg的文件中。这是一个正确的做法,如果您想在文件中保存图表而不是在浏览器中显示它。 成功创建图表…...
备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗? 一、反转链表Ⅱ 题目描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反…...

rabbitmq知识梳理
一.WorkQueues模型 Work queues,任务模型。简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息。 当消息处理比较耗时的时候,可能生产消息的速度会远远大于消息的消费速度。长此以往,消息就会堆积越来越多,…...

【数据结构与算法】动态规划法解题20240227
动态规划法 一、什么是动态规划二、动态规划的解题步骤三、509. 斐波那契数1、动规五部曲: 四、70. 爬楼梯1、动规五部曲: 五、746. 使用最小花费爬楼梯1、动规五部曲: 一、什么是动态规划 动态规划,英文:Dynamic Pro…...
备战蓝桥杯—— 双指针技巧巧答链表2
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

半监督节点分类-graph learning
半监督节点分类相当于在一个图当中,用一部分节点的类别上已知的,有另外一部分节点的类别是未知的,目标是使用有标签的节点来推断没有标签的节点 注意 半监督节点分类属于直推式学习,直推式学习相当于出现新节点后,需要…...
软件文档-运维-开发-管理-资质-评审-招投标-验收
开发文档:这类文档主要用于记录软件的开发过程和细节,包括: 《功能要求》:描述了软件应具备的功能,是软件开发的基础。《投标方案》:向潜在的客户或招标方展示公司的技术和项目实施能力。《需求分析》&…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
