数字图像学笔记 —— 17. 图像退化与复原(自适应滤波之「最小二乘方滤波」)
文章目录
- 维纳滤波的缺点
- 约束最小二乘方滤波
- 给一个实际例子吧
维纳滤波的缺点
维纳滤波(Wiener Filter),虽然是一种非常强大的退化图像还原算法,但是从实验过程我们也发现它存在着致命的缺陷,那就是要求输入退化系统的 F(u,v)F(u, v)F(u,v) 是已知的。分析维纳滤波的理论,我们发现它是通过给未知的退化系统 H(u,v)H(u, v)H(u,v) 输入原始数据 F(u,v)F(u, v)F(u,v) 后得到退化后的数据 G(u,v)G(u, v)G(u,v),然后通过梯度下降算法与约束条件 MSE=(F^−F)2MSE = (\hat F - F)^2MSE=(F^−F)2 找出最接近 H(u,v)H(u, v)H(u,v) 的近似解 H^(u,v)\hat H(u, v)H^(u,v)。
所以,在求解 H^(u,v)\hat H(u, v)H^(u,v) 的过程中,它要求我们必须要预先知道输入退化系统 H(u,v)H(u, v)H(u,v) 前的图像 F(u,v)F(u, v)F(u,v) 的信息。但是我们在实际生活中,不一定都能拥有这样的条件,可以让我们顺利的找出 H^(u,v)\hat H(u, v)H^(u,v),比方说对老照片的恢复。

拍摄时间未详的居里夫人照,图片来自网络。
对于上述图片来说,存在很明显的退化,而且我们也没有办法回到过去拍一张高清的照片,所以要想让照片得到修复,获得较好的视觉感受,维纳滤波在这里就无法使用了。
所以后续的研究者提出了一种仅依赖均值与方差便可以估算出最好复原效果的 「约束最小二乘方滤波(Constrained Least Squares Filtering)」。接下来我们来看看它是如何展现「化腐朽为神奇」的力量。
约束最小二乘方滤波
先从退化模型的一般形式(频率空间)出发,我们有如下公式:
G(u,v)=H(u,v)F(u,v)+N(u,v)G(u, v) = H(u, v) F(u, v) + N(u, v) G(u,v)=H(u,v)F(u,v)+N(u,v)
这是因为噪声函数 D(u,v)D(u, v)D(u,v) 通常被认为与输入图像 F(u,v)F(u, v)F(u,v) 相互独立,即 N(u,v)N(u, v)N(u,v) 是与 F(u,v)F(u, v)F(u,v) 不相关的噪声函数。因此,这个模型可以被看作是信号 F(u,v)F(u, v)F(u,v) 通过退化系统 H(u,v)H(u, v)H(u,v) 得到观测结果 G(u,v)G(u, v)G(u,v) 后再加上噪声 N(u,v)N(u, v)N(u,v)。
接下来,我们可以使用最小二乘法来估计未知的退化函数 H(u,v)H(u, v)H(u,v)。最小二乘法是一种优化方法,可以通过最小化误差平方和来得到最优解。具体来说,对于给定的观测结果 G(u,v)G(u, v)G(u,v) 和输入图像 F(u,v)F(u, v)F(u,v),我们可以计算出它们之间的误差平方和:
E=∑u=0M−1∑v=0N−1∣G(u,v)2−H(u,v)F(u,v)∣2E = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | G(u, v)^2 - H(u,v)F(u,v)|^2 E=u=0∑M−1v=0∑N−1∣G(u,v)2−H(u,v)F(u,v)∣2
我们的目标是找到一个 H(u,v)H(u,v)H(u,v),使得误差平方和 EEE 最小化。因此,我们可以通过求解下面的优化问题来得到最优的 H(u,v)H(u,v)H(u,v)
minH(u,v)E=∑u=0M−1∑v=0N−1∣G(u,v)2−H(u,v)F(u,v)∣2\min_{H(u,v)}E = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | G(u, v)^2 - H(u,v)F(u,v)|^2 H(u,v)minE=u=0∑M−1v=0∑N−1∣G(u,v)2−H(u,v)F(u,v)∣2
然而,我们需要加上一些约束条件,以防止退化函数 H(u,v)H(u,v)H(u,v) 变得过于复杂,从而导致过度拟合(overfitting)。一个常见的约束条件是 H(u,v)H(u,v)H(u,v) 的均值为 111,方差为 σH2\sigma^2_HσH2,即:
1MN∑u=0M−1∑v=0N−1H(u,v)=1\frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} H(u, v) = 1 MN1u=0∑M−1v=0∑N−1H(u,v)=1
1MN∑u=0M−1∑v=0N−1∣H(u,v)−1MN∑i=0M−1∑j=0N−1H(i,j)∣2=σH2\frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | H(u,v) - \frac{1}{MN} \sum_{i=0}^{M-1}\sum_{j=0}^{N-1}H(i, j) |^2 = \sigma^2_{H} MN1u=0∑M−1v=0∑N−1∣H(u,v)−MN1i=0∑M−1j=0∑N−1H(i,j)∣2=σH2
这个约束条件的意义是,我们期望退化函数 H(u,v)H(u,v)H(u,v) 的均值为 111,这是因为退化函数的总能量应该保持不变。同时,方差 σH2\sigma^2_HσH2 用于限制 H(u,v)H(u,v)H(u,v) 的复杂度,从而避免过度拟合。
根据上述约束条件,我们可以得到一个带有约束的最小二乘优化问题:
minH(u,v)E=∑u=0M−1∑v=0N−1∣G(u,v)−H(u,v)F(u,v)∣2\min_{H(u,v)} E = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | G(u,v) - H(u, v)F(u, v) |^2 H(u,v)minE=u=0∑M−1v=0∑N−1∣G(u,v)−H(u,v)F(u,v)∣2
s.t.1MN∑u=0M−1∑v=0N−1H(u,v)=1s.t. \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} H(u, v) = 1 s.t.MN1u=0∑M−1v=0∑N−1H(u,v)=1
1MN∑u=0M−1∑v=0N−1∣H(u,v)−1MN∑i=0M−1∑j=0N−1H(i,j)∣2=σH2\frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | H(u, v) - \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} H(i, j) |^2 = \sigma_{H}^{2} MN1u=0∑M−1v=0∑N−1∣H(u,v)−MN1i=0∑M−1j=0∑N−1H(i,j)∣2=σH2
上面这个优化问题可以通过拉格朗日乘子法来求解。我们首先构造一个拉格朗日函数:
L(H,λ1,λ2)=∑u=0M−1∑v=0N−1∣G(u,v)−H(u,v)F(u,v)∣2+λ1(1MN∑u=0M−1∑v=0N−1H(u,v)−1)+λ2(1MN∑u0M−1∑v=0N−1∣H(u,v)−1MN∑i=0M−1∑j=0N−1H(i,j)∣2−σH2)L(H, \lambda_1, \lambda_2) = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | G(u, v) - H(u, v)F(u, v)|^2 + \lambda_1 (\frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} H(u, v) - 1) + \lambda_2 (\frac{1}{MN} \sum_{u_0}^{M-1} \sum_{v=0}^{N-1} | H(u, v) - \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} H(i, j)|^2 - \sigma_H^2) L(H,λ1,λ2)=u=0∑M−1v=0∑N−1∣G(u,v)−H(u,v)F(u,v)∣2+λ1(MN1u=0∑M−1v=0∑N−1H(u,v)−1)+λ2(MN1u0∑M−1v=0∑N−1∣H(u,v)−MN1i=0∑M−1j=0∑N−1H(i,j)∣2−σH2)
其中 λ1\lambda_1λ1 和 λ2\lambda_2λ2 是拉格朗日乘子。接下来,我们对 L(H,λ1,λ2)L(H, \lambda_1, \lambda_2)L(H,λ1,λ2) 分别对 H(u,v)H(u,v)H(u,v)、λ1\lambda_1λ1 和 λ2\lambda_2λ2 求偏导数,并令它们等于 000,可以得到下面的一组方程:
∂L∂λ1=1MN∑u=0M−1∑v=0N−1H(u,v)−1=0\frac{\partial L}{\partial \lambda_1} = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} H(u, v) - 1 =0 ∂λ1∂L=MN1u=0∑M−1v=0∑N−1H(u,v)−1=0
∂L∂H(u,v)=−2F(u,v)(G(u,v)−H(u,v)F(u,v))+λ1+2λ2(H(u,v)−1MN∑i=0M−1∑j=0N−1H(i,j))=0\frac{\partial L}{\partial H(u, v)} = -2 F(u, v)( G(u, v) - H(u, v)F(u, v) ) + \lambda_1 + 2 \lambda_2 ( H(u, v) - \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} H(i, j)) = 0 ∂H(u,v)∂L=−2F(u,v)(G(u,v)−H(u,v)F(u,v))+λ1+2λ2(H(u,v)−MN1i=0∑M−1j=0∑N−1H(i,j))=0
∂L∂λ2=1MN∑u=0M−1∑v=0N−1∣H(u,v)−1MN∑i=0M−1∑j=0N−1H(i,j)∣2−σH2=0\frac{\partial L}{ \partial \lambda_2} = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | H(u, v) - \frac{1}{MN} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} H(i ,j) |^2 - \sigma_H^2 = 0 ∂λ2∂L=MN1u=0∑M−1v=0∑N−1∣H(u,v)−MN1i=0∑M−1j=0∑N−1H(i,j)∣2−σH2=0
解这个方程组可以得到最优的 H(u,v)H(u,v)H(u,v)。具体地,我们可以先把 λ1\lambda_1λ1 和 λ2\lambda_2λ2 消去,然后将 H(u,v)H(u,v)H(u,v) 写成矩阵形式 H=[h1,h2,...,hL]H = [h_1, h_2, ..., h_L]H=[h1,h2,...,hL],其中 L=MNL=MNL=MN。接着,将偏导数为 000 的方程写成矩阵形式 Ah=bA\textbf{h} = \textbf{b}Ah=b,其中 AAA 和 b\textbf{b}b 可以根据上述方程计算得到,h\textbf{h}h 是一个列向量,它包含了所有的 hih_ihi。最后,我们可以通过求解下面的矩阵方程来得到最优的 h\textbf{h}h:
(ATA+λI)h=ATg(A^{T} A + \lambda I) \mathbf h = A^T \mathbf g (ATA+λI)h=ATg
其中 g\textbf{g}g 是 G(u,v)G(u,v)G(u,v) 的列向量形式,III 是单位矩阵,λ\lambdaλ 是一个正则化参数,用于平衡拟合误差和模型复杂度。
最终,我们可以得到最优的 H(u,v)H(u,v)H(u,v):
H(u,v)=huN+vH(u, v) = h_{uN + v} H(u,v)=huN+v
其中 hih_ihi 是列向量 h\textbf{h}h 中的第 iii 个元素。根据最优的 H(u,v)H(u,v)H(u,v),我们可以得到修复后的图像 Frestored(u,v)F_{restored}(u,v)Frestored(u,v):
Frestored(u,v)=F−1{G(u,v)/H(u,v)}F_{restored} (u, v) = \mathcal{F}^{-1} \{ G(u,v) / H(u,v) \} Frestored(u,v)=F−1{G(u,v)/H(u,v)}
其中 F−1\mathcal{F}^{-1}F−1 是傅里叶逆变换。由于在实际应用中,H(u,v)H(u,v)H(u,v) 可能会变得过于复杂,从而导致过度拟合。为了避免这种情况,我们可以使用正则化技术,例如 Tikhonov 正则化,来控制模型的复杂度。具体来说,我们可以将优化问题改写为:
minH(u,v)E=∑u=0M−1∑v=0N−1∣G(u,v)−H(u,v)F(u,v)∣2+λ∑u=0M−1∑v=0N−1∣H(u,v)∣2\min_{H(u, v)} E = \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} | G(u, v) - H(u, v)F(u, v) |^2 + \lambda \sum_{u = 0}^{M-1} \sum_{v=0}^{N-1} | H(u, v)|^2 H(u,v)minE=u=0∑M−1v=0∑N−1∣G(u,v)−H(u,v)F(u,v)∣2+λu=0∑M−1v=0∑N−1∣H(u,v)∣2
其中 λ\lambdaλ 是一个正则化参数,用于控制 H(u,v)H(u,v)H(u,v) 的平滑度。这样,我们可以得到下面的矩阵方程:
(ATA+λI)h=ATg(A^T A + \lambda I) \textbf h = A^T \textbf g (ATA+λI)h=ATg
解这个方程可以得到带有正则化项的最优 H(u,v)H(u,v)H(u,v),从而得到修复后的图像 Frestored(u,v)F_{restored}(u,v)Frestored(u,v)。
总之,约束最小二乘方滤波是一种非常强大的图像修复技术,它可以通过仅依赖于均值和方差的约束条件来估计未知的退化函数,并从退化的图像中恢复出尽可能接近原始图像的图像。相比于维纳滤波,它更具有实用性和适用性。
给一个实际例子吧
上述内容实在太多,但是OpenCV已经帮我们减少了很多工作量,所以就可以简化为几个关键函数,所以我们就可以这样去调用它们
def ConstrainedLeastSquaresFiltering(image_path):# Load the image as grayscaleimg = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)# Add Gaussian noise to the imagenoisy_img = img + np.random.normal(0, 20, size=img.shape)# Define the degradation matrixdegradation_matrix = np.array([[0.9, 0.1, 0], [0.1, 0.8, 0.1], [0, 0.1, 0.9]])# Define the constraint matrixconstraint_matrix = np.array([[0, 1, 0], [1, -4, 1], [0, 1, 0]])# Define the regularization parameteralpha = 0.1# Compute the inverse of the degradation matrixdegradation_matrix_inv = np.linalg.inv(degradation_matrix)# Compute the constrained least squares estimatecls_estimate = cv2.filter2D(noisy_img, -1, degradation_matrix_inv)cls_estimate = cls_estimate - alpha * cv2.filter2D(cls_estimate, -1, constraint_matrix)# Convert the image to uint8 and clip it to [0, 255]cls_estimate = np.clip(cls_estimate, 0, 255).astype(np.uint8)# Show the original image, the noisy image, and the restored imagecv2.imshow("Original Image", img)cv2.imshow("Noisy Image", noisy_img)cv2.imshow("Restored Image", cls_estimate)cv2.waitKey(0)cv2.destroyAllWindows()
那么自然输出的效果就变成下面这个样子了

怎么样,是不是很厉害的技术呢?
相关文章:

数字图像学笔记 —— 17. 图像退化与复原(自适应滤波之「最小二乘方滤波」)
文章目录维纳滤波的缺点约束最小二乘方滤波给一个实际例子吧维纳滤波的缺点 维纳滤波(Wiener Filter),虽然是一种非常强大的退化图像还原算法,但是从实验过程我们也发现它存在着致命的缺陷,那就是要求输入退化系统的 …...
2023-03-05:ffmpeg推送本地视频至lal流媒体服务器(以RTMP为例),请用go语言编写。
2023-03-05:ffmpeg推送本地视频至lal流媒体服务器(以RTMP为例),请用go语言编写。 答案2023-03-05: 使用 github.com/moonfdd/ffmpeg-go 库。 先启动lal流媒体服务器软件,然后再执行命令: go…...
MathType7最新版免费数学公式编辑器
话说我也算是 MathType准资深(DB)用户了,当然自从感觉用DB不好之后,我基本上已经抛弃它了,只是前不久因为个别原因又捡起来用了用,30天试用期间又比较深入的折腾了下,也算是变成半个MathType砖家,coco玛奇朵简单介绍一下这款软件:在很可能看到这儿的你还没有出生的某个年月&…...

一文带你入门angular(中)
一、angular中的dom操作原生和ViewChild两种方式以及css3动画 1.原生操作 import { Component } from angular/core;Component({selector: app-footer,templateUrl: ./footer.component.html,styleUrls: [./footer.component.scss] }) export class FooterComponent {flag: b…...
设计多线程。)
单例设计模式共享数据问题分析、解决(c++11)设计多线程。
系列文章目录 单例设计模式共享数据问题分析、解决; 文章目录系列文章目录前言一、单例模式1.1 基本概念1.2 单例设计模式共享数据问题分析、解决1.3 std::call_once()介绍二、代码案例1.代码示例总结前言 关键内容:c11、多线程、共享数据、单例类 本章内容参考git…...

Embedding-based Retrieval in Facebook Search
facebook的社交网络检索与传统的搜索检索的差异是,除了考虑文本,还要考虑搜索者的背景。通用搜索主要考虑的是文本匹配,并没有涉及到个性化。像淘宝,youtube这些其实都是涉及到了用户自身行为的,除了搜索还有推荐&…...

xmu 离散数学 卢杨班作业详解【8-12章】
文章目录第八章 树23456810第九章46811第十章24567第十一章14571116第十二章131317第八章 树 2 (2) 设有k片树叶 2∗m2∗43∗3k2*m2*43*3k2∗m2∗43∗3k n23kn23kn23k mn−1mn-1mn−1 联立解得k9 T中有9片树叶 3 有三颗非同构的生成树 4 (1) c --abc e–abed f–dgf…...

Linux入门篇-权限管理
简介 用户管理也是和权限相关的知识点。权限的作用 权限对于普通文件和目录文件作用是不一样的 。[kioskfoundation0 ~]$ ls -l total 264 -rw-rw-r--. 2 kiosk kiosk 31943 May 29 2019 ClassPrep.txt -rw-rw-r--. 2 kiosk kiosk 7605 Jun 14 2019 ClassRHAPrep.txt -rw-rw-r…...
Linux(基于 Centos7) 常用操作
1.Linux 简介Linux 是一种 免费使用、自由传播的类 Unix 操作系统Linux操作系统内核,由林纳斯托瓦兹在1991年10月5日首次发布...Linux 是一套开源操作系统,它有稳定、消耗资源小、安全性高等特点大多数人都是直接使用 Linux 发行版(就是将 Li…...

Math类详解与Random类、三种随机数生成方式(java)
文章目录📖前言:🎀认识Random类🎀三种随机数生成方式🎀Math类的用途🎀Math类的方法📖前言: 本篇博客主要以介绍Math类的常用方法及认识Random类,及三种随机数生成方式 …...

Mac编译QT程序出现Undefined symbols for architecture x86_64
在Mac编写日志服务类, Logging_d.h内容如下 #pragma once #include <QLoggingCategory> Q_DECLARE_LOGGING_CATEGORY(hovering) Q_DECLARE_LOGGING_CATEGORY(creation) Q_DECLARE_LOGGING_CATEGORY(mouseevents) Q_DECLARE_LOGGING_CATEGORY(state) Q_DECLARE_LOGGING_C…...
蓝桥杯-李白打酒加强版
蓝桥杯-李白打酒加强版1、问题描述2、解题思路3、代码实现1、问题描述 话说大诗人李白, 一生好饮。幸好他从不开车。 一天, 他提着酒显, 从家里出来, 酒显中有酒 2 斗。他边走边唱: 无事街上走,提显去打酒。 逢店加一倍, 遇花喝一斗。 这一路上, 他一共遇到店 N 次…...
 记录第一场ABC)
AtCoder Beginner Contest 292 (A - E) 记录第一场ABC
AtCoder Beginner Contest 292 A - E前言Q1 A - CAPS LOCKQ2 Yellow and Red CardQ3 Four VariablesQ4 D - Unicyclic ComponentsQ5 E - Transitivity前言 本来晚上在打Acwing周赛,最后一题Trie想不出来咋写,看群里有人说ABC要开始了,想着没…...
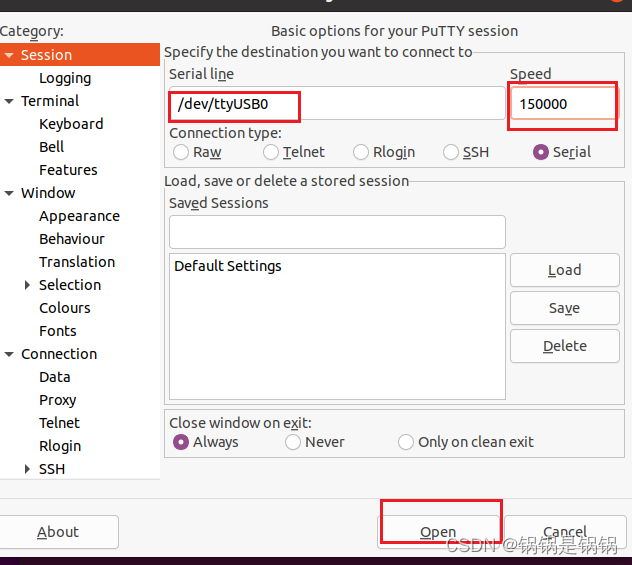
ubuntu安装使用putty
一、安装 安装虚拟机串口 sudo apt-get install putty sudo apt install -y setserial 二、使用 虚拟机连接串口 sudo setserial -g /dev/ttyS* 查看硬件对应串口 找到不是unknown的串口 sudo putty...

【CS144】Lab5与Lab6总结
Lab5与Lab6Lab汇总Lab5概述Lab6概述由于Lab5和Lab6相对比较简单(跟着文档一步一步写就行),于是放在一起做一个简单概述(主要是懒得写了…) Lab汇总 Lab5概述 lab5要求实现一个IP与Ethernet(以太网&#x…...

GDScript 导出变量 (Godot4.0)
概述 导出变量的功能在3.x版本中也是有的,但是4.0版本对其进行了语法上的改进。 导出变量在日常的游戏制作中提供节点的自定义参数化调节功能时非常有用,除此之外还用于自定义资源。 本文是(Bilibili巽星石)在4.0官方文档《GDScr…...
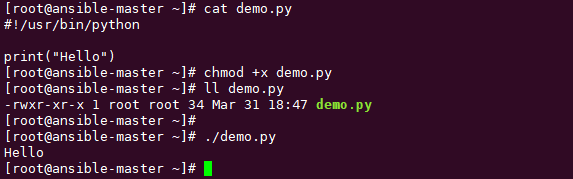
shell:#!/usr/bin/env python作用是什么
我们经常会在别人的脚本文件里看到第一行是下面这样 #!/usr/bin/python或者 #!/usr/bin/env python 那么他们有什么用呢? 要理解它,得把这一行语句拆成两部分。 第一部分是 #! 第二部分是 /usr/bin/python 或者 /usr/bin/env python 关于 #! 这个…...

计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架
报告下载: 计算机行业AIGC算力时代系列报告-ChatGPT芯片算力:研究框架 简介 “AI算力时代已经来临,计算机行业正在经历着一场前所未有的变革!” 这是一个充满活力和兴奋的时代,人工智能(AI)已…...
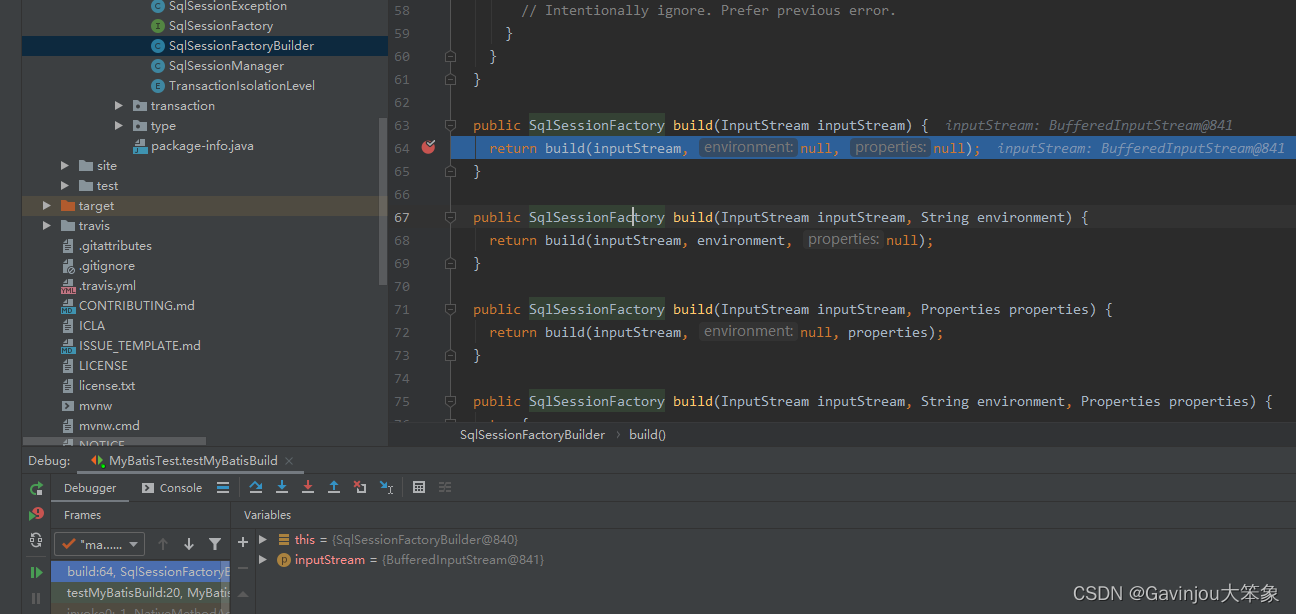
『MyBatis技术内幕』源码调试前提
准备源代码包 下载源代码 3.4.6 版本 https://github.com/mybatis/mybatis-3/releases?page2 通过 idea 导入然后回自动下载所有依赖,根据 3.4.6 版本的 pom.xml 找到依赖的 mybatis-parent 版本 <parent><groupId>org.mybatis</groupId><ar…...

# Linux最新2022年面试题大汇总,附答案
# Linux最新2022年面试题大汇总,附答案 ### [1、cp(copy单词缩写,复制功能)](最新2021年面试题大汇总,附答案.md#1cpcopy单词缩写复制功能) cp /opt/java/java.log /opt/logs/ ;把java.log 复制到/opt/logs/下 cp /…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

图解JavaScript原型:原型链及其分析 | JavaScript图解
忽略该图的细节(如内存地址值没有用二进制) 以下是对该图进一步的理解和总结 1. JS 对象概念的辨析 对象是什么:保存在堆中一块区域,同时在栈中有一块区域保存其在堆中的地址(也就是我们通常说的该变量指向谁&…...
