RL笔记:基于策略迭代求CliffWaking-v0最优解(python实现)
目录
1. 概要
2. 实现
3. 运行结果
1. 概要
CliffWalking-v0是gym库中的一个例子[1],是从Sutton-RLbook-2020的Example6.6改编而来。不过本文不是关于gym中的CliffWalking-v0如何玩的,而是关于基于策略迭代求该问题最优解的实现例。

CliffWalking-v0的游戏环境是一个4*12的网格(如上图【1】所示)。游戏规则如下:
Agent从左下角出发,在每个网格中,可以采取{UP,DOWN,RIGHT,LEFT}中任意一个动作。但是,如果采取动作后会越出边界的话,就退回原地。到达右下角的网格的话,一局游戏结束。
最下面一排网格中除了左下角(出发网格)和右下角(目标网格)以外,是所谓的悬崖网格,如果采取行动后掉入悬崖网格,会得到-100点的奖励(或者说惩罚),并且会被直接扔回出发点。其它情况下,每次行动有-1点的奖励(或者说惩罚)。Agent必需最小化到达目标网格的开销(最大化奖励,或者说最小化惩罚)。
这个游戏非常简单,不用计算,直觉就可以知道,最优策略是:在出发点向上走一格;然后在第3行一路右行;到达最右侧后向下移动一格后即到达目标网格。总的奖励是-13点。
以下给出基于策略迭代算法来求解这个问题的最优策略,看看能不能得出以上直觉上的最优策略。
2. 实现
CliffWalking-v0游戏的环境设定类似于GridWorld,所以这里采用了类似于GridWorld的状态表示方法。环境类对象创建时,用一个二维数组表示网格环境中各cell的类型,“1”表示Terminate cell;“-1”表示Cliff cells;“0”表示其它cells。如下所示:
grid = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]grid[3][11] = 1 # Terminate cellfor k in range(1,11):grid[3][11] = -1 # Cliff cells环境的转移状态函数P(s’,r|s,a)用Environment::transit_func()实现,如下所示:
def transit_func(self, state, action):"""Prob(s',r|s,a) stored in one dict[(s',reward)]."""transition_probs = {}if not self.can_action_at(state):# Already on the terminal cell.return transition_probsopposite_direction = Action(action.value * -1)for a in self.actions:prob = 0if a == action:prob = self.move_probelif a != opposite_direction:prob = (1 - self.move_prob) / 2next_state = self._move(state, a)if next_state.row == (self.row_length - 1) and 0 < next_state.column < (self.column_length - 1):reward = -100next_state = State(self.row_length - 1, 0) # Return to start grid when falls into cliff grid.else:reward = -1if (next_state,reward) not in transition_probs:transition_probs[(next_state,reward)] = probelse:transition_probs[(next_state,reward)] += probreturn transition_probsdef can_action_at(self, state):'''Assuming:grid[i][j] = 1: Terminate gridgrid[i][j] =-1: Cliff gridsgrid[i][j] = 0: Other grids'''if self.grid[state.row][state.column] == 0:return Trueelse:return Falsedef _move(self, state, action):"""Predict the next state upon the combination of {state, action}{state, action} --> next_stateCalled in transit_func()"""if not self.can_action_at(state):raise Exception("Can't move from here!")next_state = state.clone()# Execute an action (move).if action == Action.UP:next_state.row -= 1elif action == Action.DOWN:next_state.row += 1elif action == Action.LEFT:next_state.column -= 1elif action == Action.RIGHT:next_state.column += 1# Check whether a state is out of the grid.if not (0 <= next_state.row < self.row_length):next_state = stateif not (0 <= next_state.column < self.column_length):next_state = state# Entering into cliff grids is related to the correspong penalty and # reset to start grid, hence will be handled upper layer.return next_statePlanner类实现一个规划基类,进一步PolicyIterationPlanner类作为Planner子类实现了基于策略迭代的规划器,其中核心就是PolicyIterationPlanner:: policy_evaluation() 和 PolicyIterationPlanner::plan()。策略迭代算法在上一篇(RL笔记:动态规划(2): 策略迭代)中已经介绍,此处不再赘述。
PolicyIterationPlanner:: policy_evaluation()实现的是策略评估,如下所示:
def policy_evaluation(self, gamma, threshold):V = {}for s in self.env.states:# Initialize each state's expected reward.V[s] = 0while True:delta = 0for s in V:expected_rewards = []for a in self.policy[s]:action_prob = self.policy[s][a]r = 0for prob, next_state, reward in self.transitions_at(s, a):r += action_prob * prob * \(reward + gamma * V[next_state])expected_rewards.append(r)value = sum(expected_rewards)delta = max(delta, abs(value - V[s]))V[s] = valueif delta < threshold:breakreturn VPolicyIterationPlanner::plan()则实现了完整的策略迭代算法(策略评估部分调用了policy_evaluation())代码如下所示:
def plan(self, gamma=0.9, threshold=0.0001):"""Implement the policy iteration algorithmgamma : discount factorthreshold: delta for policy evaluation convergency judge."""self.initialize()states = self.env.statesactions = self.env.actionsdef take_max_action(action_value_dict):return max(action_value_dict, key=action_value_dict.get)while True:update_stable = True# Estimate expected rewards under current policy.V = self.policy_evaluation(gamma, threshold)self.log.append(self.dict_to_grid(V))for s in states:# Get an action following to the current policy.policy_action = take_max_action(self.policy[s])# Compare with other actions.action_rewards = {}for a in actions:r = 0for prob, next_state, reward in self.transitions_at(s, a):r += prob * (reward + gamma * V[next_state])action_rewards[a] = rbest_action = take_max_action(action_rewards)if policy_action != best_action:update_stable = False# Update policy (set best_action prob=1, otherwise=0 (greedy))for a in self.policy[s]:prob = 1 if a == best_action else 0self.policy[s][a] = prob# Turn dictionary to gridself.V_grid = self.dict_to_grid(V)self.iters = self.iters + 1print('PolicyIteration: iters = {0}'.format(self.iters))self.print_value_grid()print('******************************')if update_stable:# If policy isn't updated, stop iterationbreak3. 运行结果
运行结果如下(右下角可以忽视,因为到达右下角后游戏结束了,不会再有进一步的行动了):

由此可见,以上实现的确得出了跟直感相同的最优策略。
完整代码参见:reinforcement-learning/CliffWalking-v0.py
本强化学习之学习笔记系列总目录参见:强化学习笔记总目录
[1] Cliff Walking - Gym Documentation (gymlibrary.dev)
相关文章:

RL笔记:基于策略迭代求CliffWaking-v0最优解(python实现)
目录 1. 概要 2. 实现 3. 运行结果 1. 概要 CliffWalking-v0是gym库中的一个例子[1],是从Sutton-RLbook-2020的Example6.6改编而来。不过本文不是关于gym中的CliffWalking-v0如何玩的,而是关于基于策略迭代求该问题最优解的实现例。 CliffWalking-v0的…...

350. 两个数组的交集 II
两个数组的交集 II 给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结…...
Android仿微信选择图片
效果展示首先先添加用到的权限<uses-permission android:name"android.permission.INTERNET" /><!--获取手机存储卡权限--><uses-permission android:name"android.permission.READ_EXTERNAL_STORAGE"/><uses-permission android:nam…...

python+嵌入式——串口通信篇(收发解包)
目录前言安装pyserialpyserial大致概括整体流程硬件连接例子(简单版)详细使用serial初始化参数发包收包收包检查包并解包python struct模块结语前言 这几年,自己也做了一些嵌入式机器人。在整个开发的过程中,调通信通常会花费一段比较长的时间ÿ…...
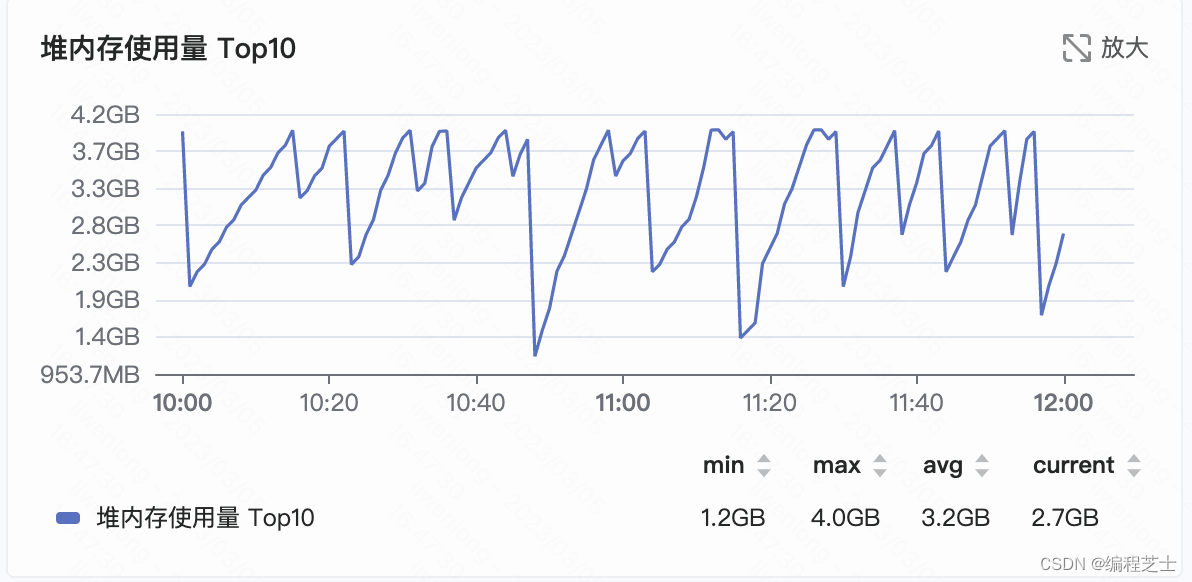
剖析G1 垃圾回收器
简单回顾 在Java当中,程序员在编写代码的时候只需要创建对象,从来不需要考虑将对象进行释放,这是因为Java中对象的垃圾回收全部由JVM替你完成了(所有的岁月静好都不过是有人替你负重前行)。 而JVM的垃圾回收由垃圾回收器来负责,在…...
如何打造一款专属于自己的高逼格电脑桌面
作为一名电脑重度使用者,你是否拥有一款属于你自己的高逼格电脑桌面呢?你是不是也像大多数同学一样,会把所有的内容全部都堆积到电脑桌面,不仅找东西困难,由于桌面内容太多还会导致C盘空间不足,影响电脑的反…...

【C++】string的使用及其模拟实现
文章目录1. STL的介绍1.1 STL的六大组件1.2 STL的版本1.3 STL的缺陷2. string的使用2.1 为什么要学习string类?2.2 常见构造2.3 Iterator迭代器2.4 Capacity2.5 Modifiers2.6 String operations3. string的模拟实现3.1 构造函数3.2 拷贝构造函数3.3 赋值运算符重载和…...

怀念在青鸟的日子
时间过的可真快,一转眼来到了2023年!我初中上完就没有在念,下了学门步入社会,那时的我一片迷茫,不知道该去干什 么,父母说要不去学挖掘机、理发、修车...我思考再三,一个都没有我喜欢的…...

学习记录---Python内置类型
文章目录字符串split()列表常见操作列表相减字典创建普通创建eval(s)添加或更新元素d[t] 1d.update({c: 3}){**d1, **d2} **字典解包装运算符删除元素 d.pop(c)属性d.items()d.keys()d.values()访问元素d[Name]d.get(score)遍历字典for key in dictfor key, values in dict.it…...
Python笔记 -- 列表
文章目录1、列表简介2、修改、添加、删除元素2.1、添加2.2、删除3、排序、倒序4、遍历列表5、创建数值列表6、列表切片7、列表复制8、元组1、列表简介 在Python中用方括号[]表示列表,用逗号隔开表示其元素 通过索引访问列表 names [aa,bb,cc,dd]print(names[0]) …...

谈谈UVM中的uvm_info打印
uvm_info宏的定义如下: define uvm_info(ID,MSG,VERBOSITY) \begin \if (uvm_report_enabled(VERBOSITY,UVM_INFO,ID)) \uvm_report_info (ID, MSG, VERBOSITY, uvm_file, uvm_line); \end 从这里可以看出uvm_info由两部分组成:uvm_report_enabled(VER…...
)
矩阵理论1 集合上的等价关系(equivalence relations on a set S)
定义 对于一个集合S, 如果集合E⊂SS\mathcal{E} \subset S\times SE⊂SS满足以下条件 自反性: 对于∀s∈S,都有(s,s)∈E\forall s\in S, 都有 (s, s) \in \mathcal{E}∀s∈S,都有(s,s)∈E对称性: (s,t)∈E⇔(t,s)∈E(s,t) \in \mathcal{E} \Leftrightarrow (t,s)\in \mathcal…...
【网络监控】Zabbix详细安装部署(最全)
文章目录Zabbix详细安装部署环境准备安装依赖组件访问初始化配置Zabbix详细安装部署 Zabbix 是一个高度集成的网络监控解决方案,可以提供企业级的开源分布式监控解决方案,由一个国外的团队持续维护更新,软件可以自由下载使用,运作…...

阿里云轻量服务器--Docker--Nacos安装(使用外部Mysql数据存储)
前言:docker 安装nacos 如果不设置外部的mysql 默认使用内嵌的内嵌derby为数据源,这个时候如果,重新部署nacos 则会造成原有数据丢失情况; 1 默认安装的nacos 启动后使用的是内嵌的存储: 2 使用外部mysql 作为存储&a…...
unity开发知识点小结01
unity对象生命周期函数 Awake():最早调用,所以可以实现单例模式 OnEnable():组件激活后调用,在Awake后调用一次 Stat():在Update()之前,OnEnable…...

软件系统[软件工程]
What’s the link? They all involve outdated (legacy) software technology. All have had huge socio-economical impact. Prompting national lockdowns. Spreadsheet workflow error led to thousands of preventable infections and deaths. Huge losses of citizen dat…...
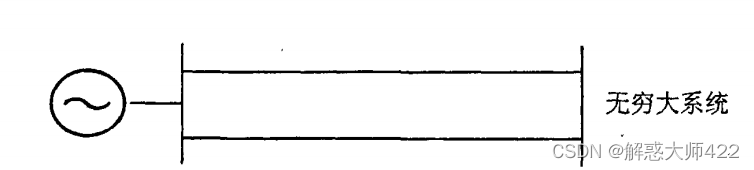
电力系统稳定性的定义与分类
1电力系统稳定性的定义与分类 IEEE给出电力系统稳定性定义:电力系统稳定性是指电力系统这样的一种能力—对于给定的初始运行状态,经历物理扰动后,系统能够重新获得运行平衡点的状态,同时绝大多数系统变量有界,因此整个…...
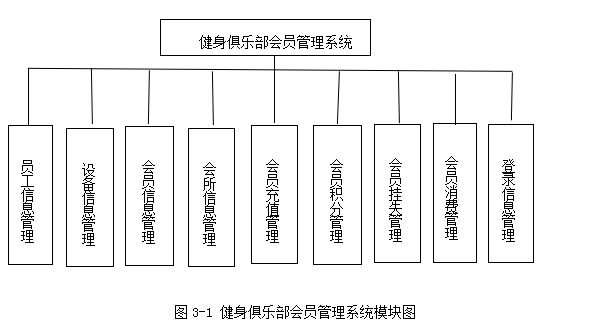
基于java的俱乐部会员管理系统
技术:Java、JSP等摘要:随着科学技术的飞速发展,科学技术在人们日常生活中的应用日益广泛,也给各行业带来发展的机遇,促使各个行业给人们提供更加优质的服务,有效提升各行业的管理水平。俱乐部通过使用一定的…...
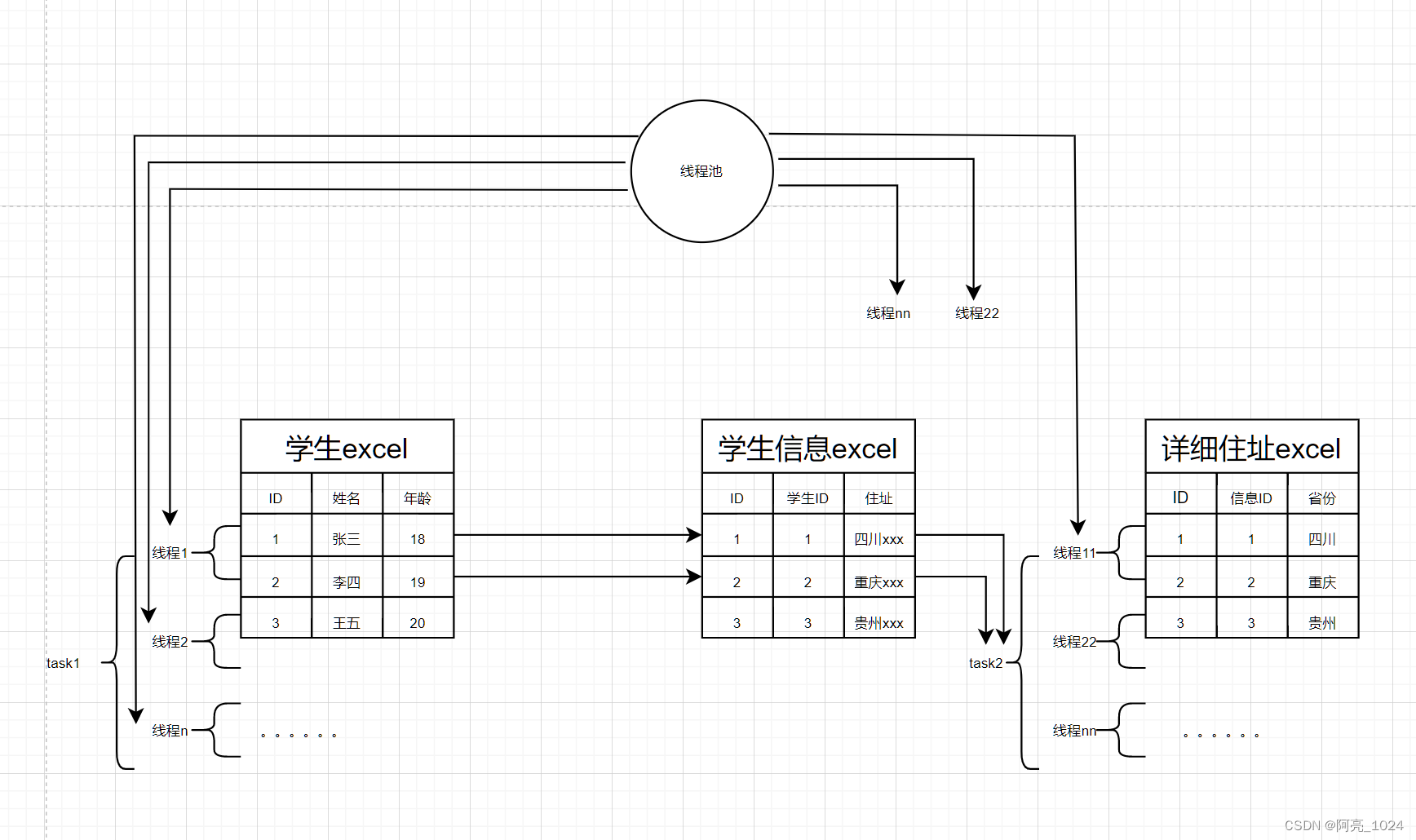
线程池执行父子任务,导致线程死锁
前言, 一次线程池的不当使用,导致了现场出现了线程死锁,接口一直不返回。而且由于这是一个公共的线程池,其他使用了次线程池的业务也一直阻塞,系统出现了OOM,不过是幸好是线程同事测试出来的,没…...
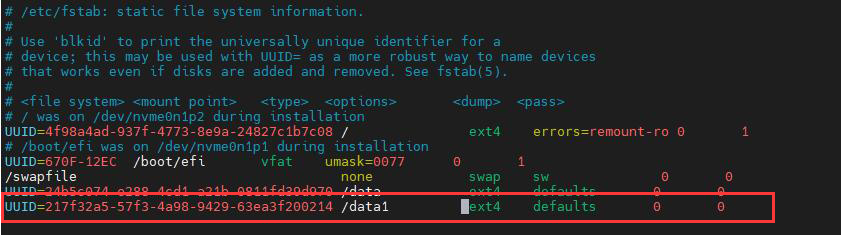
Ubuntu系统新硬盘挂载
Ubuntu系统新硬盘挂载 服务器通常会面临存储不足的问题,大部分服务器都是ubuntu系统,该篇博客浅浅记载一下在ubuntu系统上挂载新硬盘的步骤。本篇博文仅仅记载简单挂载一块新的硬盘,而没有对硬盘进行分区啥的。如果需要更加完善的教程&#…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

C++实现分布式网络通信框架RPC(2)——rpc发布端
有了上篇文章的项目的基本知识的了解,现在我们就开始构建项目。 目录 一、构建工程目录 二、本地服务发布成RPC服务 2.1理解RPC发布 2.2实现 三、Mprpc框架的基础类设计 3.1框架的初始化类 MprpcApplication 代码实现 3.2读取配置文件类 MprpcConfig 代码实现…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
