信息安全与数学基础-笔记-④二次同余方程
知识目录
- 二次同余方程的解
- 欧拉判别式
- Legendre (勒让德符号)
二次同余方程的解
- 什么是二次同余方程的解
注意这里二次同余方程和一次同余方程是不一样的
在x2x^2x2 三 a (mod m) 方程中举例 ↓
解即剩余类,因为是模m,所以我们在 [ 0, m-1 ]中逐个代入看是否满足方程式。 - 解的说法有三种:
①平方剩余
②平方非剩余
要满足这两种情况的条件:(a,m)= 1,首先要互素,其次再代入完全剩余系看有没有解
③既不是平方剩余也不是平方非剩余
这种情况是在(a,m) 不是互素的情况下,即使是有解,也不是平方剩余和平方非剩余 - 只需要代入一半的完全剩余系的数字
如下图所示,因为x2x^2x2在模的世界里,m-x与x是差一个正负符号而已,在二次方程式中正好解决了该问题,那么就可以利用该特性,只需要在完全剩余系中找解的时候,
代入一半即可[0,m/2 ] or [ m/2, m],代入哪一半都行,这两部分代入后结果是一样的。
解释:将下图的m-x平方展开后就明白为什么只需要代入一半(记住:是要模m的)

欧拉判别式
上面讲述了二次同余方程的解是从何而来,如何找解。那么欧拉判别式就是用来判断一个解是否是二次同余方程式的平方剩余或者平方非剩余
- 使用欧拉判别式的条件
方程式:x2x^2x2 三 a (mod p)
1:p必须是奇素数(奇素数,不包括2)
2:(a, p) = 1,ap必须互素
(很显然必须要互素,因为本身判断的就是平方剩余/非剩余的关系,开头已经讲清楚了)
满足以上条件则:
若aaa(^((p^pp−^-−1^11)^))/^//2^22 三 1 (mod p),则a是平方剩余。
若aaa(^((p^pp−^-−1^11)^))/^//2^22 三 -1 (mod p),则a是平方非剩余。

Legendre (勒让德符号)
设p为奇素数,(a, p)= 1,则 ↓
若:(ap\frac{a}{p}pa) = 1 ,则a为平方剩余
若:(ap\frac{a}{p}pa) = -1 ,则a为平方非剩余
(ap\frac{a}{p}pa)就叫做a对p的勒让德符号
其实就是用了上面的欧拉判别式↓↓
aaa(^((p^pp−^-−1^11)^))/^//2^22 三 1 (mod p)
aaa(^((p^pp−^-−1^11)^))/^//2^22 三 -1 (mod p)
下面围绕勒让德符号展开一些推论和定理:
- (1p\frac{1}{p}p1) = 1 (证明可以使用欧拉判别式,1的多少次方终究还是1)
- (−1p\frac{-1}{p}p−1) = (−1)p−12(-1)^\frac{p-1}{2}(−1)2p−1 (本条推论就是欧拉判别式)
- (2p\frac{2}{p}p2) = (−1)p2−18(-1)^\frac{p^2-1}{8}(−1)8p2−1
勒让德符号中可以像分子那样拆开,没有限制条件。

相关文章:

信息安全与数学基础-笔记-④二次同余方程
知识目录二次同余方程的解欧拉判别式Legendre (勒让德符号)二次同余方程的解 什么是二次同余方程的解 注意这里二次同余方程和一次同余方程是不一样的 在x2x^2x2 三 a (mod m) 方程中举例 ↓ 解即剩余类,因为是模m,所以我们在 [ 0, m-1 ]中逐个代入看是…...

Luogu P4447 [AHOI2018初中组]分组
题目链接:传送门 将nnn个可重复的整数分为mmm组,每组中的数必须连续且不重复,使人数最少的组人数最多。 两个最值肯定第一想到二分,每次二分出一个值,判断在这个值为答案的前提下能否完成分组。 在思考判别函数时发现…...
手把手创建flask项目
Flask 框架流程 什么是Flask: Flask诞生于2010年, 使用python语言基于Werkzeug工具箱编写的轻量级Web开发框架 Flask本身相当于一个内核, 其他几乎所有的功能都要用到扩展(邮件:Flask-Mail, 用户认证:Flask-Login, 数据库:Flask-SQLAlchemy). Flask的核心在于Werkz…...

SpringCloud-4_Eureka服务注册与发现
Eureka作为一个老牌经典的服务注册&发现技术,其设计和理念,也在影响后面的组件。目前主流的服务注册&发现的组件是Nacos当前项目架构问题分析-引出Eureka问题分析:1.在企业级项目中,服务消费访问请求会存在高并发2.如果只…...

【react全家桶】生命周期
文章目录04 【生命周期】1.简介2.初始化阶段2.1 constructor2.2 componentWillMount(即将废弃)2.3 static getDerivedStateFromProps(新钩子)2.4 render2.5 componentDidMount2.6 初始化阶段总结3.更新阶段3.1 componentWillRecei…...
虚拟机安装Windows 10
虚拟机安装Windows 10 镜像下载 方法一:下载我制作好的镜像文件->百度网盘链接 提取码:Chen 方法二:自己做一个 进入微软官网链接 下载"MediaCreationTool20H2" 运行该工具 点击下一步选择路径,等他下载好就欧克了…...

【CMU15-445数据库】bustub Project #2:B+ Tree(下)
Project 2 最后一篇,讲解 B 树并发控制的实现。说实话一开始博主以为这块内容不会很难(毕竟有 Project 1 一把大锁摆烂秒过的历史x),但实现起来才发现不用一把大锁真的极其痛苦,折腾了一周多才弄完。 本文分基础版算法…...

leetcode 困难 —— 外星文字典(拓扑排序)
题目: 现有一种使用英语字母的外星文语言,这门语言的字母顺序与英语顺序不同。 给定一个字符串列表 words ,作为这门语言的词典,words 中的字符串已经 按这门新语言的字母顺序进行了排序 。 请你根据该词典还原出此语言中已知的字…...
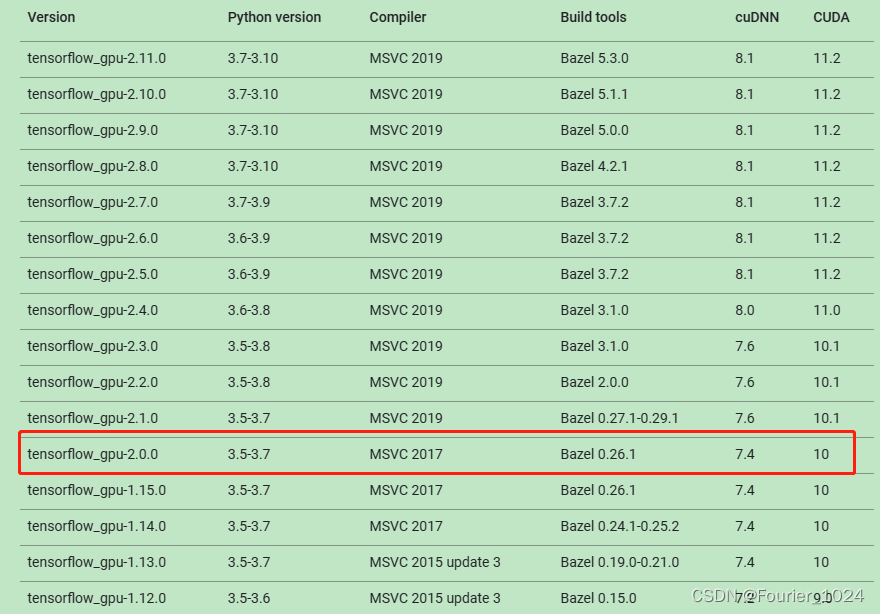
ubuntu server 18.04使用tensorflow进行ddqn训练全过程
0. 前言 需要使用ddqn完成某项任务,为了快速训练,使用带有GPU的服务器进行训练。记录下整个过程,以及遇到的坑。 1. 选择模板代码 参考代码来源 GitHub 该代码最后一次更新是Mar 24, 2020。 环境配置: python3.8 运行安装脚本…...

2023年全国最新二级建造师精选真题及答案14
百分百题库提供二级建造师考试试题、二建考试预测题、二级建造师考试真题、二建证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 二、多选题 61.已经取得下列资质的设计单位,可以直接申请相应类别施工总承包一级…...
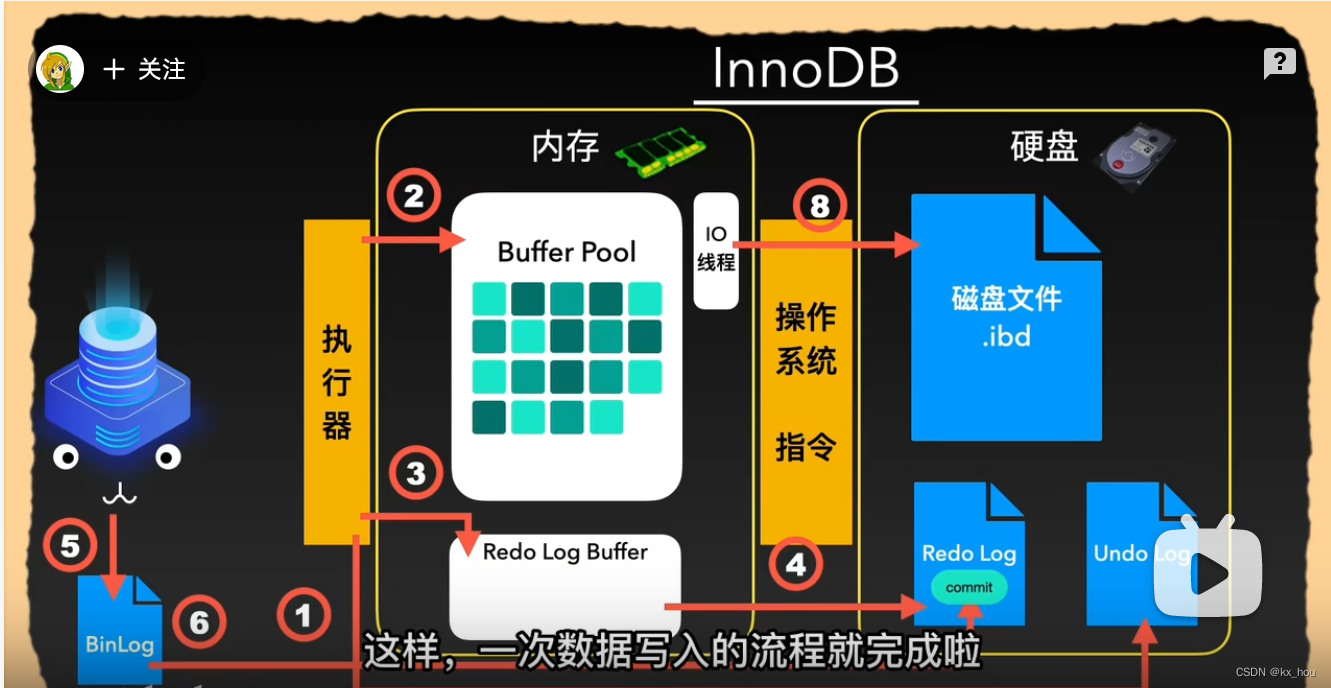
mysql一条语句的写入原理
mysql写入原理 我们知道在mysql数据库最核心的大脑就是执行引擎; 其中的默认引擎Innodb在可靠执行和性能中做出来平衡; innodb支持在事务控制、读写效率,多用户并发,索引搜索方面都表现不俗; innodb如何进行数据写入…...
)
嵌入式Linux内核代码风格(二)
第九章:你已经把事情弄糟了 这没什么,我们都是这样。可能你的使用了很长时间Unix的朋友已经告诉你“GNU emacs”能 自动帮你格式化C源代码,而且你也注意到了,确实是这样,不过它所使用的默认值和我们 想要的相去甚远&a…...
Spring Boot @Aspect 切面编程实现访问请求日志记录
aop切面编程想必大家都不陌生了,aspect可以很方便开发人员对请求指定拦截层,一般是根据条件切入到controller控制层,做一些鉴权、分析注解、获取类名方法名参数、记录操作日志等。 在SpringBoot中使用aop首先是要导入依赖如下: …...

初学者的第一个Linux驱动
软件环境:Ubuntu20.04 Linux内核源码:3.4.39 硬件环境:GEC6818 什么是驱动?简单来说就是让硬件工作起来的程序代码。 Linux驱动模块加载有两种方式: 1、把写好的驱动代码直接编译进内核。 2、把写好的驱动代码编…...

7. 拼数
1 题目描述 拼数成绩10开启时间2021年09月24日 星期五 18:00折扣0.8折扣时间2021年11月15日 星期一 00:00允许迟交否关闭时间2021年11月23日 星期二 00:00 设有 n个正整数 a[1]…a[n],将它们联接成一排,相邻数字首尾相接,组成一个最大的整…...

Java每天15道面试题 | Redis
redis 和 和 memcached 什么区别?为什么高并发下有时单线程的 redis 比多线程的memcached 效率要高? 区别: 1.mc 可缓存图片和视频。rd 支持除 k/v 更多的数据结构; 2.rd 可以使用虚拟内存,rd 可持久化和 aof 灾难恢复࿰…...

13_pinctrl子系统
总结 pinctrl作为驱动 iomuxc节点在设备树里面 存储全部所需的引脚配置信息 iomux节点匹配pinctrl子系统 控制硬件外设的时候 要知道有哪些gpio 再看gpio有哪些服用寄存器 接着在程序配置gpio相关寄存器 这样搞效率很低 所以用iomux节点保存所有的引脚组 pinctrl驱动起来的时…...

Linux系统对于实施人员的价值
Linux系统对于实施人员的价值 随着互联网的发展,linux系统越来越突显了巨大的作用,很多互联网公司,政府企业,只要用到服务器的地方几乎都能看到linux系统的身影,可以说服务是不是在linux系统跑的代表了企业的技术水平&…...

ForkJoin 和 Stream并行流
还在用 for 循环计算两个数之间所有数的和吗?下面提供两种新方法! 1. ForkJoin 1.1 背景 要知道,在一个方法中,如果没有做特殊的处理,那么在方法开始到结束使用的都是同一个线程,无论你的业务有多复杂 那…...

逻辑优化-cofactor
1. 简介 逻辑综合中的Cofactor优化方法是一种重要的逻辑优化技术。它通过提取逻辑电路中的共同部分,从而简化电路、减小面积和延迟。该方法广泛应用于电子设计自动化(EDA)领域中的逻辑综合、等价转换和优化等方面。 Cofactor优化方法最早由…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
