766. 托普利茨矩阵
给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。
如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。
示例 1:
输入:matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出:true
解释:
在上述矩阵中, 其对角线为:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”。
各条对角线上的所有元素均相同, 因此答案是 True 。
示例 2:
输入:matrix = [[1,2],[2,2]]
输出:false
解释:
对角线 “[1, 2]” 上的元素不同。
提示:
m == matrix.length
n == matrix[i].length
1 <= m, n <= 20
0 <= matrix[i][j] <= 99
思路:
正常来讲,最直观的做法应该就是第一行的每个元素开始向右下方遍历,看看是否相等;然后再沿着第一列开始向右下方遍历,看看是否相等。
但其实你仔细思考一下,就会发现,不需要这么麻烦,满足题意的最基本的条件,不就是每个元素都跟左上方的元素相等么(如果存在的话)。
而且第一行和第一列是不用判断的,因为不存在左上方元素。
代码:
class Solution {
public:bool isToeplitzMatrix(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();for(int i = 0 ; i < n ; i++){for(int j = 0 ; j < m ; j++){if(i-1 >= 0 && j-1 >= 0){if(matrix[i-1][j-1] == matrix[i][j])continue;elsereturn false;}}}return true;}
};
相关文章:

766. 托普利茨矩阵
给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。 如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。 示例 1: 输入:matr…...

基于STM32的汽车防窒息系统
文章目录 基于STM32的汽车防窒息系统系统简介材料展示视频制作硬件连接原理图PCB实物图GSM模块使用GSM模块代码 SGP30模块SGP30模块代码 步进电机驱动步进电机代码 其他模块主逻辑代码 总结 基于STM32的汽车防窒息系统 系统简介 随着社会的发展目前汽车的流行,汽车大…...
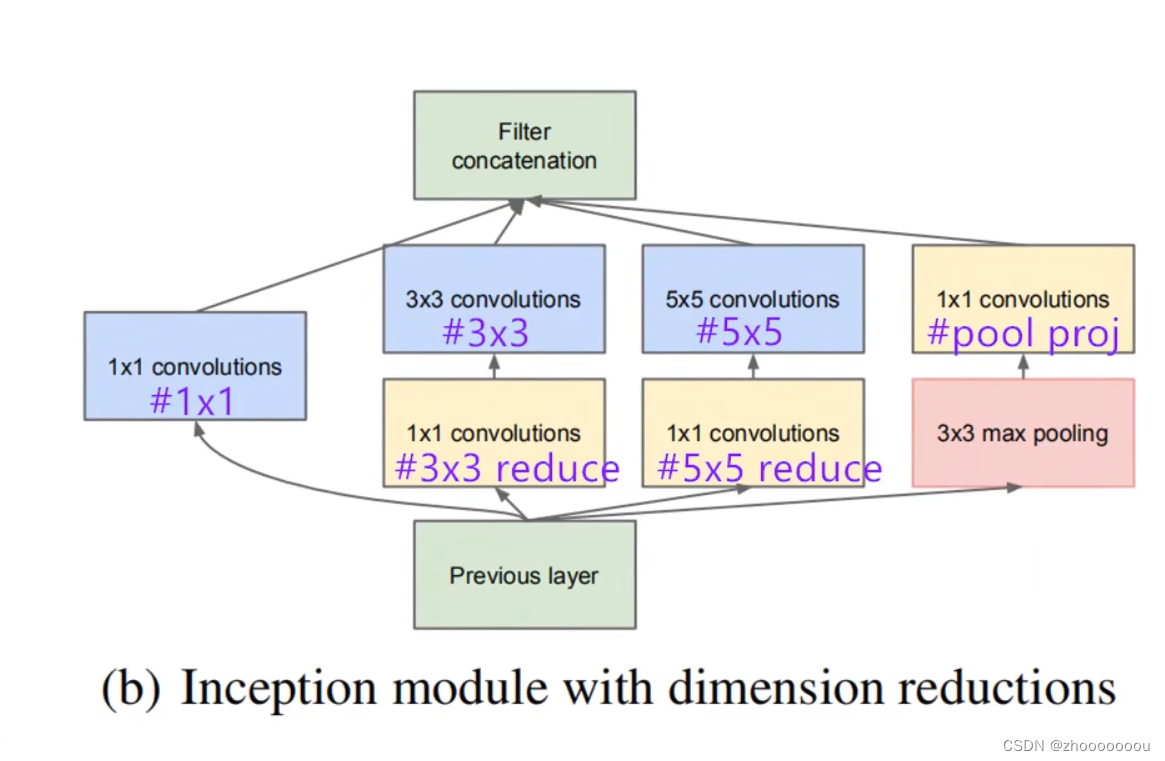
GoogleNet神经网络介绍
一、简介 GoogleNet,也称为GoogLeNet,是谷歌工程师设计的一种深度神经网络结构,它在2014年的ImageNet图像识别挑战赛中取得了冠军。该神经网络的设计特点主要体现在其深度和宽度上,通过引入名为Inception的核心子网络结构&#x…...

AI水下颜色校正解决方案,助力企业打造水下视觉盛宴
水下摄影作为一种独特且富有挑战性的拍摄方式,正受到越来越多旅行者和摄影师的青睐。然而由于海水的光线折射和金属成分的影响,水下拍摄的照片和视频往往存在严重的偏色问题,无法真实还原水下世界的美丽与神奇。美摄科技凭借深厚的技术积累和…...
LINUX笔记温习
目录 DAY1 DAY2 day3: day4 day5 day6 day7 day8 day9 day10 day11 day12 day13 day14 day15 20day DAY1 1、多层级文件夹创建要带-p; 2、创建多文件,要先到该目录下才能创建(第一个目录必须存在才能有效建立); D…...

钉钉服务端API报错 43008 参数需要multipart类型
钉钉服务端API报错 43008 参数需要multipart类型 problem 使用媒体文件上传接口,按照文档输入参数,结果返回报错 # 参数 {"access_token": "xxx""type": "image","media": "/Users/xxx/xxx/s…...
HarmonyOS NEXT应用开发案例——阻塞事件冒泡
介绍 本示例主要介绍在点击事件中,子组件enabled属性设置为false的时候,如何解决点击子组件模块区域会触发父组件的点击事件问题;以及触摸事件中当子组件触发触摸事件的时候,父组件如果设置触摸事件的话,如何解决父组…...

【C语言】联合和枚举
个人主页点这里~ 联合和枚举 一、联合体1、联合体类型的声明2、联合体成员的特点3、与结构体对比4、计算联合体大小 二、枚举1、枚举的声明2、枚举的优点3、枚举类型的使用 一、联合体 1、联合体类型的声明 联合体的定义与结构体相似,但是联合体往往会节省更多的空…...
苹果手机黑屏打不开怎么办?5种方法让你轻松应对
苹果手机以其卓越的性能和流畅的操作体验赢得了全球用户的喜爱。然而,就像其他电子产品一样,苹果手机偶尔也会遇到一些问题。其中,苹果手机黑屏打不开是许多用户都曾遇到过的困扰。当您按下电源键,却发现手机屏幕一片漆黑…...

鸿蒙:滑动条组件Slider
滑动条组件,通常用于快速调节设置值,如音量调节、亮度调节等应用场景。 说明 该组件从API Version 7开始支持。 子组件 无 接口 Slider(options?: {value?: number, min?: number, max?: number, step?: number, style?: SliderStyle, direc…...

【智能家居项目】RT-Thread版本——DHT11获取温湿度 | MQTT上传到服务器 | 服务器控制外设
🐱作者:一只大喵咪1201 🐱专栏:《智能家居项目》 🔥格言:你只管努力,剩下的交给时间! 这篇文章中,本喵将使用RT-Thread Studio来实现这个智能家居的项目,最终…...
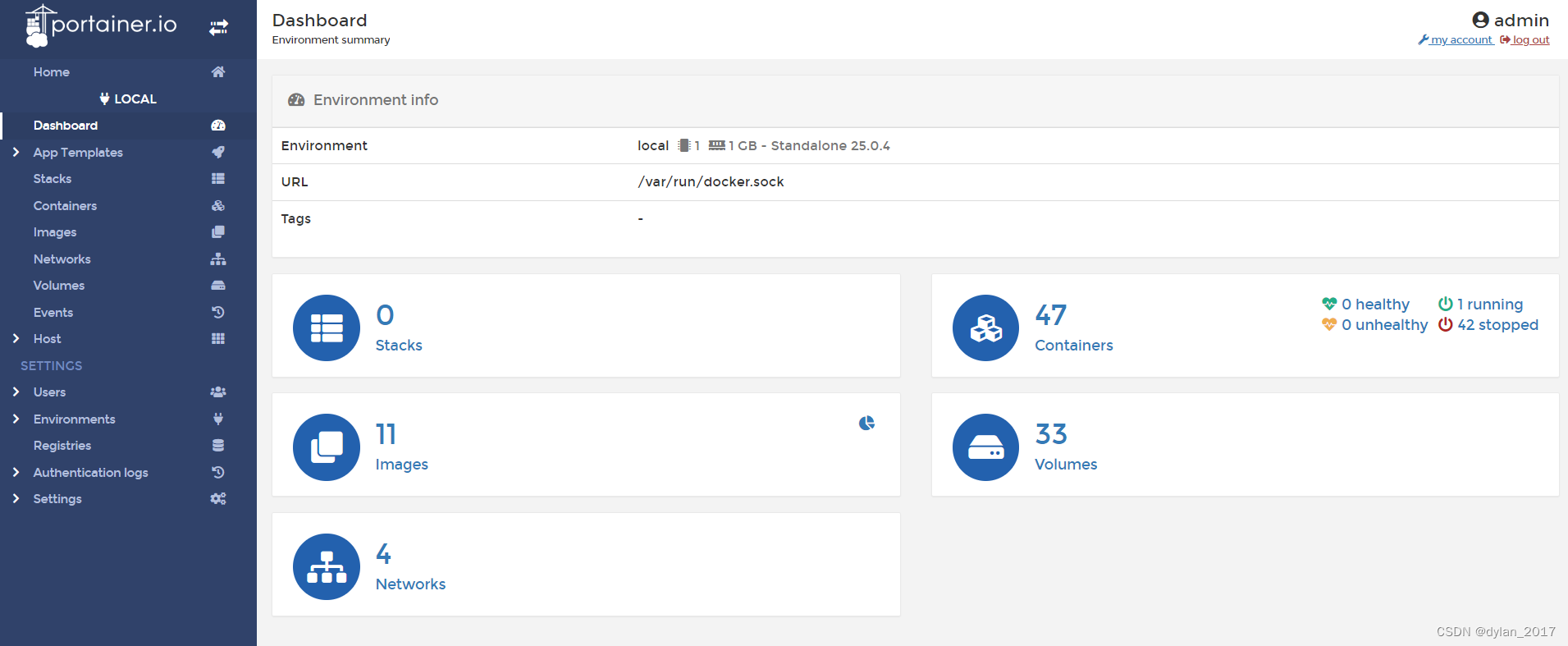
Docker 轻量级可视化工具 Portainer
1. 是什么 它是一款轻量级的应用,它提供了图形化界面,用于方便管理Docker环境,也包括单机环境和集群环境。 2. 安装 官网:Kubernetes and Docker Container Management Software 安装路径:Install the Compose plug…...

推特Twitter有直播功能吗?如何用Twitter直播?
现在各大直播平台已经成为社交媒体营销的一种重要渠道,它让品牌能够即时地与全球受众进行互动。据统计,直播市场正在迅速增长,预计到2028年将达到2230亿美元的规模。在这个不断扩张的市场中,许多社交媒体平台如YouTube、Facebook、…...
:素数,埃式筛法,快速幂,斐波那契与矩阵幂运算)
蓝桥杯算法基础(32):素数,埃式筛法,快速幂,斐波那契与矩阵幂运算
素数 有些人认为一个人一生中有三个周期,从他或她出生的那一天开始。 这三个周期是身体周期,情感周期的和智力的周期,他们有周期的长度为23,28, 和33天。每一个周期都有一个高峰。在一个周期的高峰期, 一个…...

VSCode - 离线安装扩展python插件教程
1,下载插件 (1)首先使用浏览器打开 VSCode 插件市场link (2)进入插件主页,点击右侧的 Download Extension 链接,将离线安装包下载下来(文件后缀为 .vsix) 2,…...

2024年中级职称现在报名,时间还太早了吗?什么时候合适?
甘建二十年耕耘职称,关于职称大小事都了解 想要评湖北职称,请认准甘建二,关于职称评审条件、申报时间、评审资料、申报材料、评审流程、证书查询、出证时间、考试答辩等关于职称所有的事情都知道,找甘建二准没错。 我们通常都会觉…...
》)
《责任链模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 模式说明 方案: 责任链模式将请求的发送者和接收者解耦,构成一个链条,并由多个对象对请求进行处理,直到找到合适的处理者为止。优点: …...

【学习】JMeter和Postman两种测试工具的主要区别有哪些
Postman和JMeter都是常用的API测试工具,但它们之间存在一些不同之处。以下是Postman和JMeter的主要区别: 语言支持 Postman是一个基于Chrome的应用程序,因此它使用JavaScript作为编程语言。这意味着你可以使用JavaScript来编写测试脚本和断…...

【压缩字符串算法解析与实现】
压缩的要求是将连续相同字符替换为字符 数字形式,例如 “AAABCCDDDD” 变为 “A3BC2D4”。 问题描述与分析 给定一个字符串,我们需要判断是否可以进行压缩,并且只在压缩后的字符串长度比原字符串长度更短时进行压缩。如果字符串可以压缩&a…...

test02
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...
