K邻算法:在风险传导中的创新应用与实践价值
01 前言
在当今工业领域,图思维方式与图数据技术的应用日益广泛,成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考,不仅促进业界爱好者之间的交流,更期望从技术层面为企业在图数据库选型时提供新的视角与思路。
02 K邻算法的实践意义
K邻算法(K-Hop Neighbor),即K跳邻居算法,是一种基于广度优先搜索(BFS)[1] 的遍历策略,用于探索起始节点周围的邻域。该算法在关系发现、影响力预测、好友推荐等预测类场景中得到了广泛应用。
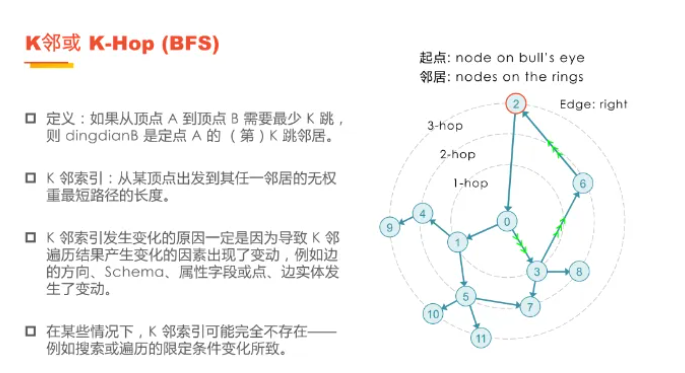
图1 在图数据库中基于广度优先遍历的K邻查询
在图论中,沿着一条边移动被视为一跳(hop)。在遍历图中的顶点时,我们需要考虑多跳问题。图论起源于数学家欧拉在1836年提出的哥尼斯堡七桥问题,它奠定了图计算的数学基础。自20世纪80年代以来,图计算技术迅速发展,成为现代计算领域的重要组成部分。
在现实世界中,危机的传播正是K邻搜索的一个典型应用。以发生危机的实体为起点,顺着或逆着(取决于边的具体定义)边的方向进行1步、2步、3步乃至更深层次的查询,得到的就是先后会被危机波及到的实体。
03 创新应用与案例分析
以某知名房地产企业HD的供应链图谱为例,我们可以通过持股方向、资金流向等信息,清晰直观地揭示危机的传播路径和传递对象。
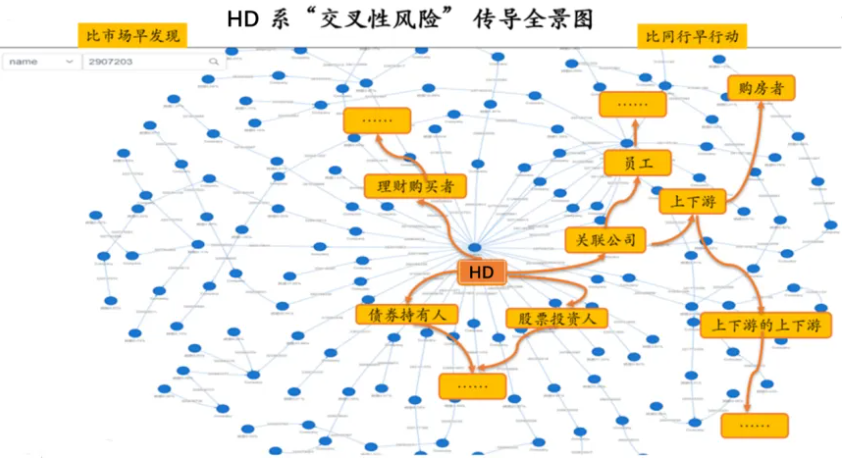
图2 HD系“交叉性风险”传导全景图
以HD为例,危机发生后,风险传播路径如下:
-
第一层:影响HD的关联公司;
-
第二层:影响公司员工和供应商;
-
第三层:影响购房者(供应商停止供货、工人停工,可能导致HD的在建工程停滞)。
-
……
风险从HD集团开始,逐步扩散至关联公司、员工、供应商、购房者等,形成了一张复杂的“网络”,呈现出明显的“链条效应”。
然而,许多与风险传导相关的实际应用并未采用图计算,而是依赖于手工计算,如银行KYC部门在计算UBO时仍使用Excel表。这种做法的效率和准确率可想而知。这与金融机构IT系统的陈旧和工作方法的落后有直接关系,阻碍了业务的开展,如企业影响力分析。
企业影响力分析不仅涉及持股关系、生产供求关系等传统问题,还应包括与企业相关的所有金融行为和事件,以及与这些行为事件直接或间接相关的事务。分析的视角不应仅限于企业实体,而应扩展至企业发布的产品、债券等。
如图3所示,分析的核心是企业的某个债券,其价格下跌可能直接影响其他债券的价格:
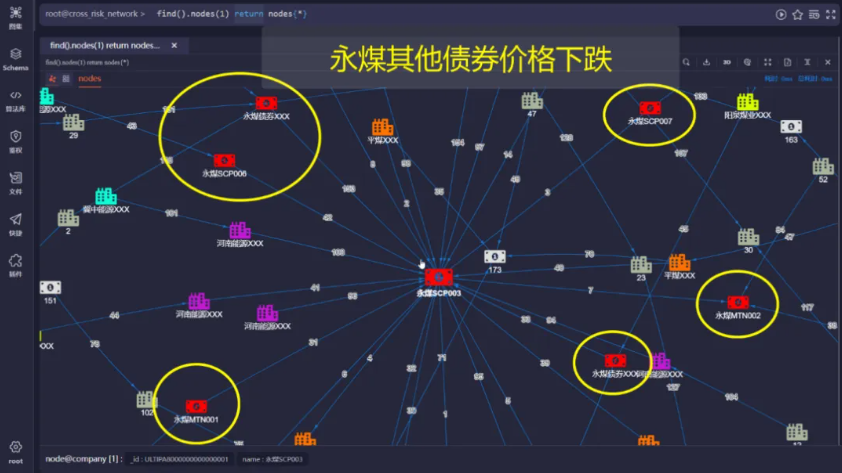
图3 某债券价格下跌影响该公司其他债券的价格
图4则标出了持有该债券的、可能受影响的省内其他企业:

图4 某债券价格下跌影响持有该债券的其他公司
图3和图4展示的是该债券的1步邻居,从这些邻居继续向外探寻就能得到该债券价格下跌后产生的危机传递效应,如图5所示:

图5 某债券价格下跌影响整个债券市场
专家们已越来越认识到,金融风险并不是孤立存在的,不同风险间具有链条效应,任何一只蝴蝶扇动翅膀,都有可能造成跨市场的风险传染——风险的关联性具有相互转化、传递和耦合的特点——图技术与蝴蝶效应在本质上是不谋而合的,即通过深度挖掘不同来源的数据,以网络化分析的方式去洞察。
此外,金融场景是一种基于长链条计算的场景,这就导致技术实现时的规则更为复杂,因为会涉及到各种回溯、归因,而且数据的计算量更大,同时也更注重时效性。只有实现真正的实时、全面、深度穿透、逐笔追溯、精准计量的监测和预警,才能保障金融风控中不会出现“蝴蝶效应”式的风险发生。
值得注意的是,图往往包含着复杂的属性及定义,例如:边的有向、无向,边的属性权重,K 邻是否包含 K-1 邻,如何处理计算环路等等,这些问题会导致 K 邻算法具体实现的差异。此外,在一些实际场景中,图自身拓扑结构的变化,过滤条件的设定,节点、边属性的变化都会影响到 K 邻计算的结果。
在行业应用中,K邻算法通常应用于多模态的异构图,即将多个单一信息的图融合在一起形成的综合性图谱。这对算法实现者的数据收集和构图能力提出了高要求,同时也对K邻算法的灵活性和功能性提出了更高标准。嬴图的高密度并发图算法库是目前全球运行最快、最丰富的图算法集合,支持通过EXTA接口进行热插拔和扩展。
如果在公开资料中看到K邻算法的应用多是同构图(只有一种点、一种边),可能是因为作者想通过简单的例子阐明观点,或者因为构图能力不足限制了算法的应用,也可能是K邻算法的实现不尽人意,无法对异构图进行恰当处理。K邻算法的应用应该是广泛且实际的,能够解决现实问题的,如果是因为后面两种情况而限制了算法的“大展宏图”,那么相关图厂商就应该反思一二并提高自身了!
最后,一个优秀的算法设计不仅应具备解决问题的能力,还应关注计算效率,即算力。我们列举了一些高性能图计算系统应具备的核心能力,以供企业在评估市场上各种图计算产品时作为参考:
-
高速图搜索能力:高QPS/TPS、低延时,实时动态剪枝能力;
-
对任何规模图的深度、实时搜索与遍历能力(10层以上);
-
高密度、高并发图计算引擎:极高的吞吐率;
-
成熟稳定的图数据库、图计算与存储引擎、图中台等;
-
可扩展的计算能力:支持垂直与水平可扩展;
-
3D+2D高维可视化、高性能的知识图谱Web前端系统;
-
便捷、低成本的二次开发能力(图查询语言、API/SDK、工具箱等)。
K邻算法:在风险传导中的创新应用与实践价值
本文摘编自《图算法:行业应用与实践》,经出版方授权发布。

延伸阅读《图算法:行业应用与实践》
推荐语:这是一本全面讲解当下主流图算法原理与工程实践的著作,旨在帮助读者在分析和处理各种复杂的数据关系时能更好地得其法、善其事、尽其能。本书概念清晰、内容丰富、实用性强、语言流畅,深入浅出、重点突出,既适合入门读者阅读,又适合有一定图数据库基础的进阶人员阅读。
相关文章:

K邻算法:在风险传导中的创新应用与实践价值
01 前言 在当今工业领域,图思维方式与图数据技术的应用日益广泛,成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考,不仅促进业界爱好者之间的交流,更期望从技术层面为企业在图数…...

【小白的大模型之路】基础篇:Transformer细节
基础篇:Transformer 引言模型基础架构原论文架构图EmbeddingPostional EncodingMulti-Head AttentionLayerNormEncoderDecoder其他 引言 此文作者本身对transformer有一些基础的了解,此处主要用于记录一些关于transformer模型的细节部分用于进一步理解其具体的实现机…...
Golang | Leetcode Golang题解之第73题矩阵置零
题目: 题解: func setZeroes(matrix [][]int) {n, m : len(matrix), len(matrix[0])col0 : falsefor _, r : range matrix {if r[0] 0 {col0 true}for j : 1; j < m; j {if r[j] 0 {r[0] 0matrix[0][j] 0}}}for i : n - 1; i > 0; i-- {for …...
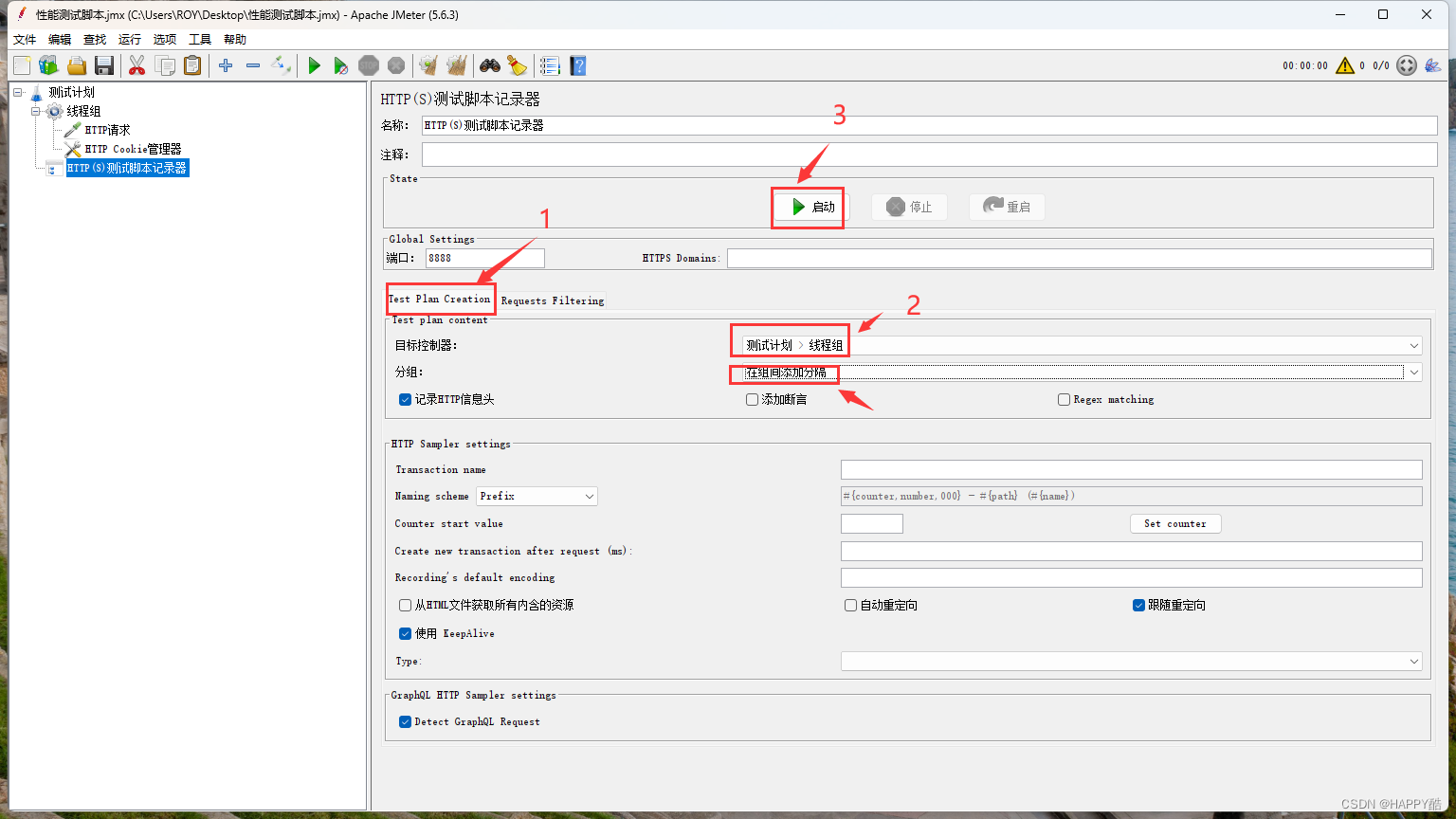
JMeter性能压测脚本录制
第一步:电脑打开控制面板设置代理服务器 第二步:jmeter的测试计划添加一个HTTP(S)脚本记录器 在脚本记录器里配置好信息,然后保存为脚本文件(.*表示限定) 此方框内容为项目地址(可改…...

缓存雪崩、缓存击穿、缓存穿透是什么、之间的区别及解决办法
缓存雪崩、缓存击穿、缓存穿透: 详细介绍看这篇文章,写得很好: 什么是缓存雪崩、缓存击穿、缓存穿透 下面是我自己总结的,比较简单清楚地展示了缓存雪崩、缓存击穿和缓存穿透的根本区别和相应的解决办法。强烈建议看完上述文章后…...

Pytorch张量广播
Pytorch 中的主要的数据结构包括标量、向量、矩阵、张量,同时支持数据之间的运算。在 Pytorch 中有一个张量广播的概念,就是要把小的放大,最后在一起做计算,并不是所有的张量都可以计算,规则如下 首先比较维度&#x…...
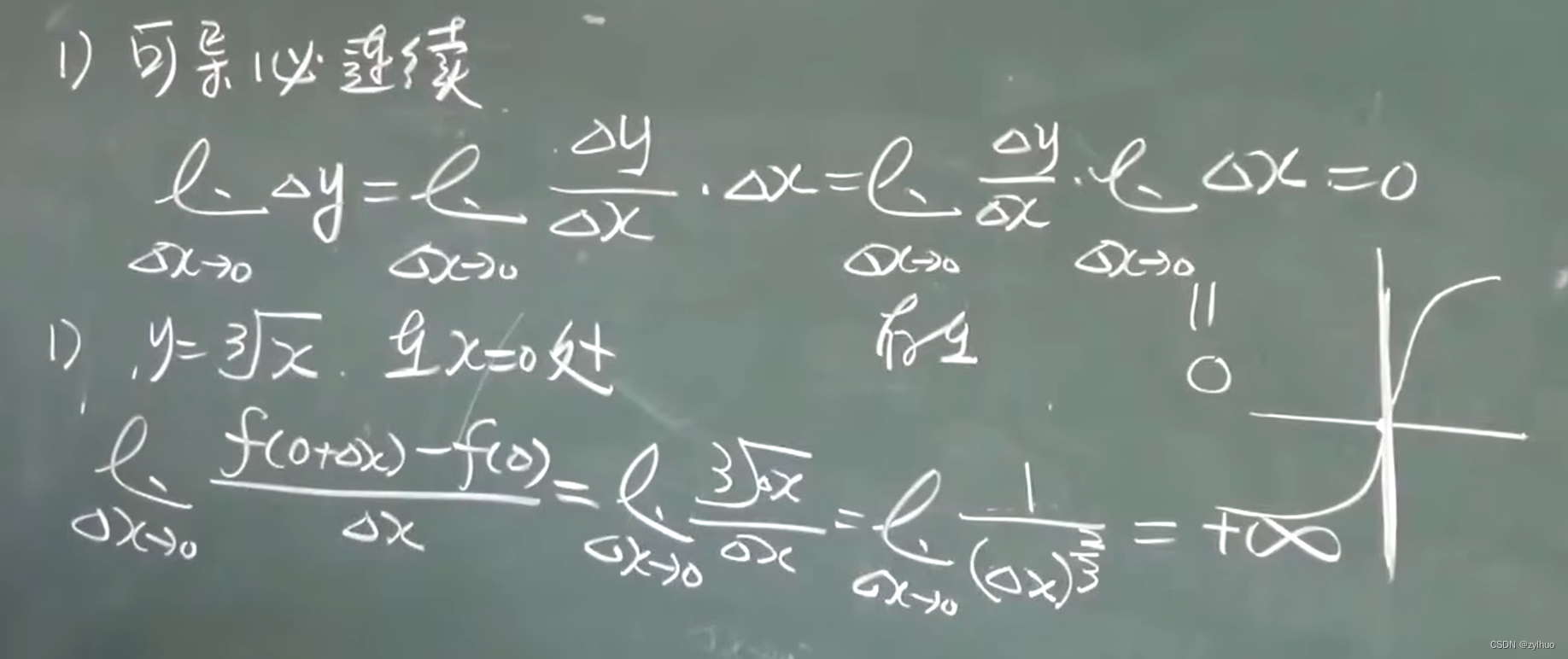
AI算法-高数2-导数定义和公式
P14 2.1 导数的定义(一):2.1 导数的定义_哔哩哔哩_bilibili 导数定义: 导数公式: P15 2.1 导数的定义(二):2.1 导数的定义(二)_哔哩哔哩_bilibili [a,b]可导,a的端点:右可导,b端点&…...

Vitis HLS 学习笔记--AXI_STREAM_TO_MASTER
目录 1. 简介 2. 示例 2.1 示例功能介绍 2.2 示例代码 2.3 顶层函数解释 2.4 综合报告(HW Interfaces) 2.5 关于TKEEP和TSTRB 2.6 综合报告(SW I/O Information) 3. 总结 1. 简介 本文通过“<Examples>/Interface…...
WPF之可翻转面板
1,创建翻转面板的资源字典:FlippPanel.xaml。 无外观控件同样必须给样式指定类型( <ControlTemplate TargetType"ss:FlipPanel">),相关详情参考:WPF之创建无外观控件-CSDN博客)…...
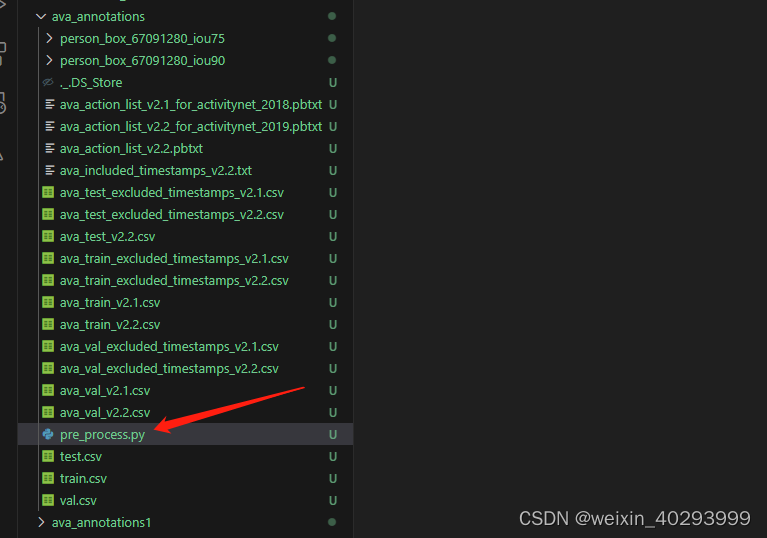
【深度学习】--slowfast视频理解数据集处理pipeline
官网指引: facebookresearch SlowFast :https://github.com/facebookresearch/SlowFast 进入dataset:https://github.com/facebookresearch/SlowFast/blob/main/slowfast/datasets/DATASET.md 这里面的东西需要通读,但是不要过于…...

ArcGIS10.2能用了10.2.2不行了(解决)
前两天我们的推文介绍了 ArcGIS10.2系列许可到期解决方案-CSDN博客文章浏览阅读2次。本文手机码字,不排版了。 昨晚(2021\12\17)12点后,收到很多学员反馈 ArcGIS10.2系列软件突然崩溃。更有的,今天全单位崩溃。提示许…...
mysql查询表信息(表名、表结构、字段信息等)
MySQL中,您可以使用以下SQL查询数据库的表信息或者某个表中具体的信息,例如:字段、字段描述、索引等,以下为具体的SQL: 1、查询数据库所有表信息(表名/表描述) SELECTtable_name name,TABLE_C…...

【MySQL探索之旅】JDBC (Java连接MySQL数据库)
📚博客主页:爱敲代码的小杨. ✨专栏:《Java SE语法》 | 《数据结构与算法》 | 《C生万物》 |《MySQL探索之旅》 |《Web世界探险家》 ❤️感谢大家点赞👍🏻收藏⭐评论✍🏻,您的三连就是我持续更…...
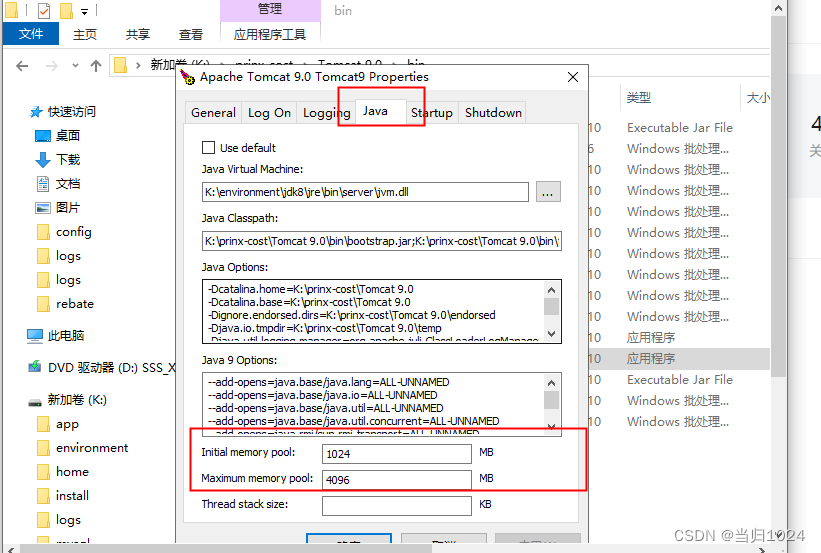
tomcat-GC溢出
背景 一个项目需要导出大量的数据,导致GC但是这个项目在本地能够运行,但是在服务器上就不能运行本地和服务器的区别:NGINX和TOMCATGC和NGINX无关,那么就是Tomcat分配JVM的堆内存的容量不够 错误解决思路 网上教了一些查看JVM的大小…...

结合场景,浅谈深浅度拷贝
有两段代码是这样的: A段: List<String> list1 new ArrayList<>(); Bear B new Bear(); for(Apple apple : apples){B.url apple.url;B.content apple.content;list1.add(Bear); } B段: List<String> list1 new A…...
生成指定范围的随机整数
private static final Random RANDOM new Random();// 生成指定范围的随机整数public static int generateRandomInt(int min, int max) {return RANDOM.nextInt(max - min 1) min;}public static void main(String[] args) {Integer count 5;Integer randomInt generateR…...

少的缓存穿透是缓存击穿,大量的是缓存雪崩
只要请求穿过了缓存层,直接打到了数据库,我就把这个现象理解为缓存穿透。 只要缓存失效了,就会出现缓存穿透,然后根据失效缓存数量的多少,划分出缓存击穿和缓存雪崩 缓存一致性 先改redis再改mysql。...

设备能耗数据在线监测
在追求可持续发展和绿色经济的当下,企业对于设备能耗的管理愈发重视。设备能耗数据在线监测,不仅能帮助企业实时掌握设备的运行状况,还能为企业节能减排、降低运营成本提供有力支持。HiWoo Cloud平台凭借其先进的技术和丰富的经验,…...

springboot整合websocket,超简单入门
springBoot整合webSocket,超简单入门 webSocket简洁 WebSocket 是一种基于 TCP 协议的全双工通信协议,它允许客户端和服务器之间建立持久的、双向的通信连接。相比传统的 HTTP 请求 - 响应模式,WebSocket 提供了实时、低延迟的数据传输能力。…...

代码随想录算法训练营第三十四天| 860.柠檬水找零 406.根据身高重建队列 452. 用最少数量的箭引爆气球
860.柠檬水找零 题目链接 思路 三种情况,一种贪心,在bill为20时,有一次贪心选择:优先考虑先找105,再考虑找3*5,因为5可以用于bill10和bill20两种情况 解题方法 第一种:bill5,直接收 第二种…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
