秋招突击——算法打卡——5/28——复习{Z字形变换、两数之和}——新做:{整数反转、字符串转整数}
文章目录
- 复习
- Z字形变换
- 实现代码
- 参考代码
- 两数之和
- 复习代码
- 新作
- 整数反转
- 个人实现
- 实现代码
- 参考做法
- 字符串转换整数
- 个人解法
- 分析总结
复习
Z字形变换



实现代码
- 这里使用了他的思想,但是没有用他的代码,虽然已经比上次简洁了,但是还是不够,在学习一下他的代码!
string convert(string s,int numRows){string res[numRows];string r ;if (numRows == 1 ) return s;for (int i = 0; i < s.size(); ++i) {if (i % (2 * numRows - 2) == 0)res[0] += s[i];if(i % (2 * numRows - 2) == (numRows - 1))res[numRows - 1] += s[i];else{for (int j = 1; j < numRows - 1; ++j) {if(i % (2 * numRows - 2) == j || i % (2 * numRows - 2) == (2 * numRows - 2 - j))res[j] += s[i];}}}for (int i = 0; i < numRows; ++i) {r += res[i];}return r;}
参考代码
string convert(string s,int n){string r ;if (n == 1 ) return s;// 分别遍历一下numRows还有整个字符串for (int i = 0; i < n; ++i) {if(i == 0 || i == n - 1)for (int j = i; j < s.size(); j += (2 * n -2)) {r += s[j];} elsefor (int j = i,k = 2 * n - 2 - i; j < s.size() || k < s.size();j += (2 * n -2) , k += (2 * n -2)) {if(j < s.size()) r += s[j];if(k < s.size()) r += s[k];}}return r;}
两数之和
- 这题很清晰,就是模拟两个数字的相加过程,需要注意的是,就是三个数相加,分别是节点1、节点2、还有addNum,有一个不为空,就继续往上加

复习代码
注意
- 创建一个临时头节点,方便操作
- 操作指针,要判定当前指针是否为空
- 指针记得向后移动
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {auto dummy = new ListNode(),cur = dummy;int addNum = 0;while(l1 || l2 || addNum){if(l1) addNum += l1->val ,l1 = l1->next;if(l2) addNum += l2->val ,l2 = l2->next;cur->next = new ListNode(addNum % 10);cur = cur->next;addNum = addNum / 10;}return dummy->next;}
新作
整数反转

个人实现
- 因为int类型存储有限,所以想的是直接使用string类型的数据进行处理,就不用担心对应的超范围问题,然后使用stoi函数。同时超过范围的检测,也是使用string进行遍历检测。
不过,今天又是一遍过!
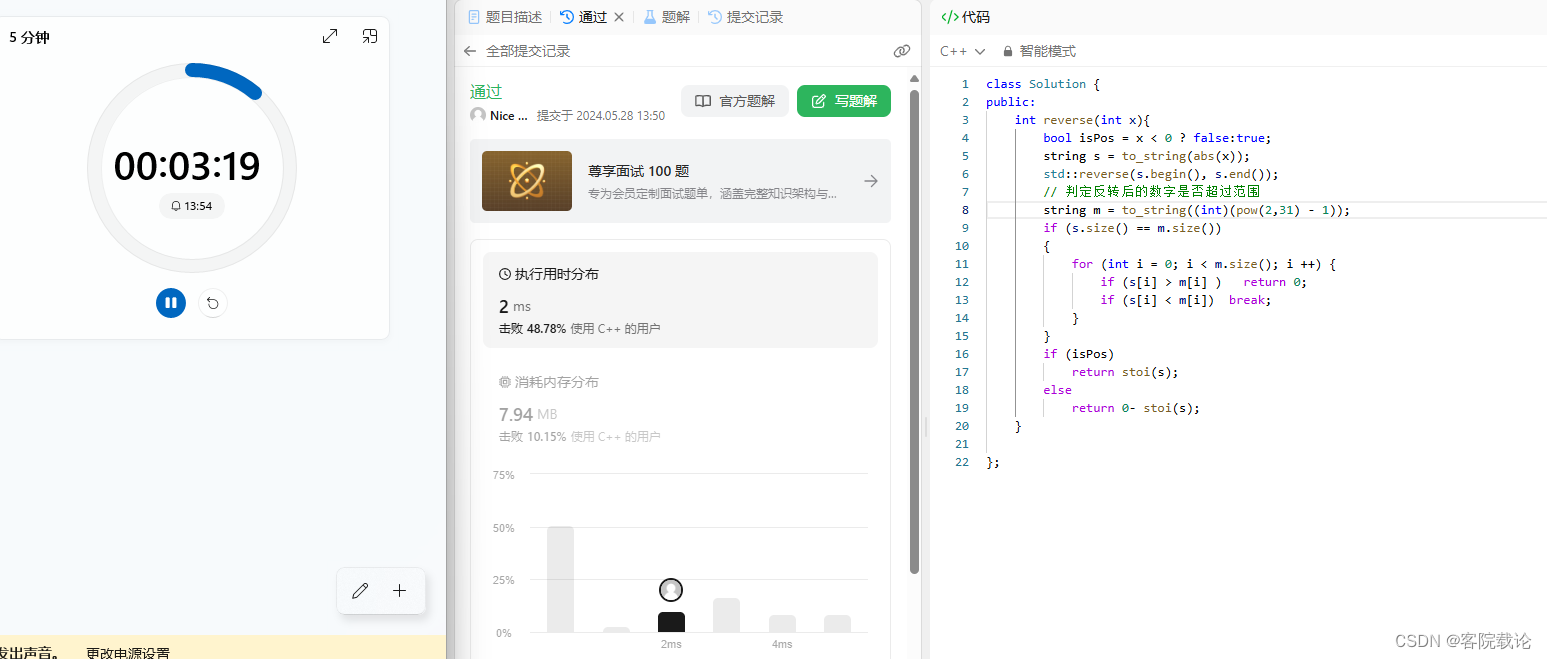
实现代码
int reverse(int x){bool isPos = x < 0 ? false:true;string s = to_string(abs(x));std::reverse(s.begin(), s.end());// 判定反转后的数字是否超过范围string m = to_string((int)pow(2,31) - 1);if (s.size() == m.size()){for (int i = 0; i < m.size(); i ++) {if (s[i] > m[i] ) return 0;if (s[i] < m[i]) break;}}if (isPos)return stoi(s);elsereturn 0- stoi(s);}
参考做法
-
通过求余10,来获取当前的位数,然后通过乘以10,来变成对应的数字
-
如果不能存储超过范围的数字,那就通过因式变化实现。

- 下述想法实现的确实比我的简洁很多,而且操作字符串,确实比操作数字要慢很多。
- 字符串底层实现reverse的时间复杂度是,底层是通过反转迭代器来实现的,双指针同时遍历,所以时间复杂度是O(n),和这个算法差不多,只不过我有多遍历了一次判定是否越界。
- 如果会溢出,就变换形态。
int reverse(int x){int r = 0;while (x){if (r > 0 && r > (INT_MAX - x % 10) / 10) return 0;if (r < 0 && r < (INT_MIN - x % 10) / 10) return 0;r = r * 10 + x % 10;x /= 10;}return r;
}
字符串转换整数
题目链接

个人解法
- 单纯逐个遍历,然后根据不同的情况进行不同的操作,执行效果如下。逻辑比较松散,需要看看官方思路是怎么做的,会不会完整一点。
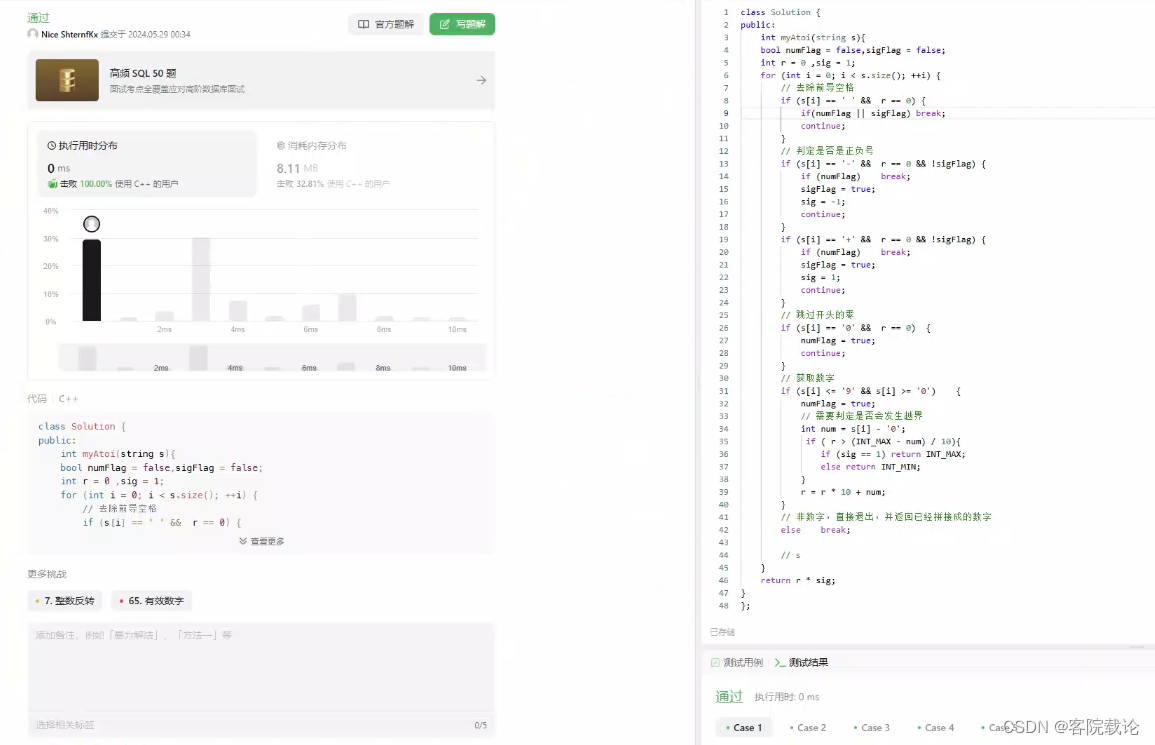
class Solution {
public:int myAtoi(string s){bool numFlag = false,sigFlag = false;int r = 0 ,sig = 1;for (int i = 0; i < s.size(); ++i) {// 去除前导空格if (s[i] == ' ' && r == 0) {if(numFlag || sigFlag) break;continue;}// 判定是否是正负号if (s[i] == '-' && r == 0 && !sigFlag) {if (numFlag) break;sigFlag = true;sig = -1;continue;}if (s[i] == '+' && r == 0 && !sigFlag) {if (numFlag) break;sigFlag = true;sig = 1;continue;}// 跳过开头的零if (s[i] == '0' && r == 0) {numFlag = true;continue;}// 获取数字if (s[i] <= '9' && s[i] >= '0') {numFlag = true;// 需要判定是否会发生越界int num = s[i] - '0';if ( r > (INT_MAX - num) / 10){if (sig == 1) return INT_MAX;else return INT_MIN; }r = r * 10 + num;}// 非数字,直接退出,并返回已经拼接成的数字else break;// s}return r * sig;
}
};
分析总结
- 时间来不及了,今天就不看官方参考了,明天要准备面试了!
相关文章:

秋招突击——算法打卡——5/28——复习{Z字形变换、两数之和}——新做:{整数反转、字符串转整数}
文章目录 复习Z字形变换实现代码参考代码 两数之和复习代码 新作整数反转个人实现实现代码 参考做法字符串转换整数个人解法 分析总结 复习 Z字形变换 实现代码 这里使用了他的思想,但是没有用他的代码,虽然已经比上次简洁了,但是还是不够&…...
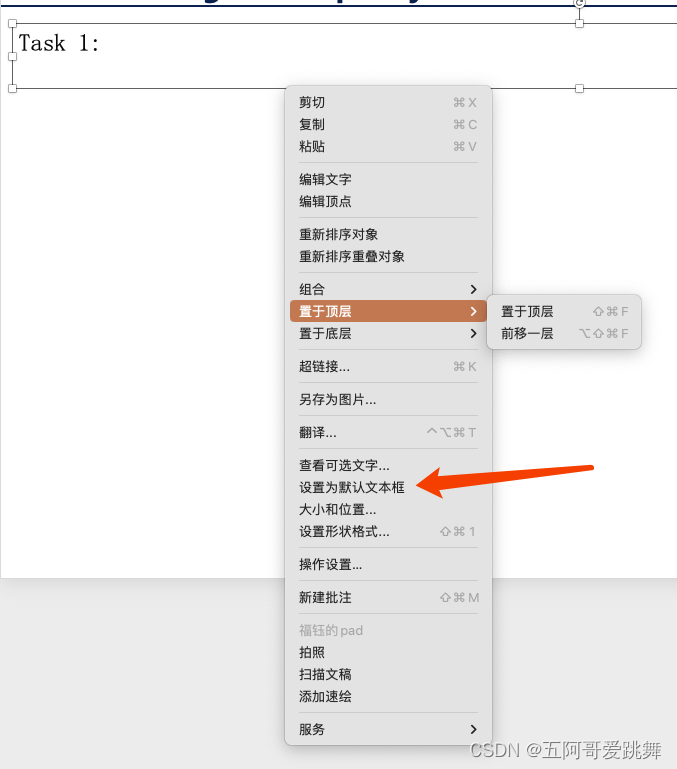
PPT设置为本框的默认格式以及固定文本框
调整文本框固定位置 双击文本框之后勾选如下三个位置 设置文本框为默认 在调整好文本框的基本性质后,设置为默认即可...

计算机基础(5)——进制与进制转换
💗计算机基础系列文章💗 👉🍀计算机基础(1)——计算机的发展史🍀👉🍀计算机基础(2)——冯诺依曼体系结构🍀👉ἴ…...

发现情绪背后的真实心理需求,选择适合你的情绪调节方式
一、教程描述 心态对人的生活质量以及身体健康等多方面,都会产生非常重要的影响,受到不良情绪的影响,人的心态也会发生一定的变化。对于处于不良情绪状态的人来讲,应该重视学会调整自己的情绪。在心理学上,人的每种情…...
代理记账公司的五大问题及其解决方案
代理记账公司是现代企业管理中不可或缺的一部分,它为企业的日常运营提供了专业、高效的服务,随着行业的发展和竞争的加剧,代理记账公司的面临的问题也日益突出,这些问题主要表现在以下几个方面: 业务流程不规范 许多代…...
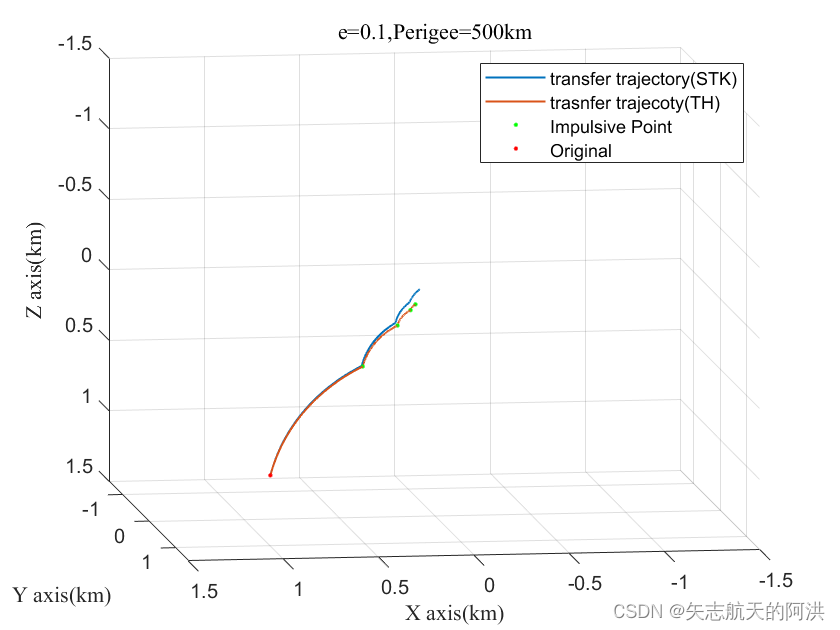
TH方程学习 (7)
一、内容介绍 TH存在广泛应用,在下面案例中,将介绍几种相对运动模型,斜滑接近模型,本节学习斜滑接近制导方法能够对接近时间、接近方向以及自主接近过程的相对速度进行控制。施加脉冲时刻追踪器的位置连线可构成一条直线…...
2024最新python入门教程|python安装|pycharm安装
前言:在安装PyCharm之前,首先需要明确PyCharm是一款功能强大的Python集成开发环境(IDE),由JetBrains公司开发。PyCharm旨在通过提供智能代码补全、语法高亮、代码检查、快速导航和重构等丰富的编码辅助工具,…...

docker架构
docker架构 Docker daemon 是Docker最核心的后台进程,它负责响应来自Dockerclient的请求,然后将这此请求翻译成系统调用完成容器管理操作。该进程会在后台后启动一个APIServer,负责接收由 Dockerclient发送的请求;接收到的请求将通…...
使用Java进行网络采集:代理IP与参数传递详解
在Java编程语言中,参数传递机制是一个常见的讨论话题。理解这一点对于编写高效且无错误的Java代码至关重要。本文将探讨Java的参数传递机制,解析其究竟是“按引用传递”还是“按值传递”,并结合网络爬虫技术的实例,展示如何在实际…...

多功能光时域反射仪的工作原理
6426A-2101多功能光时域反射仪是新一代掌上型智能化光纤通信测量仪器,具有强大的功能和广泛的应用领域。它能够显示光纤及光缆的损耗分布曲线图,测量光纤及光缆的多种关键参数,包括长度、损耗、接续质量等,为光纤通信系统的工程施…...

目标检测数据集 - 海洋垃圾检测数据集下载「包含VOC、COCO、YOLO三种格式」
数据集介绍:海洋垃圾检测数据集,真实拍摄海洋海底场景高质量垃圾检测图片数据,涉及场景丰富,比如海底塑料垃圾数据、海底铁制品罐状垃圾数据、海底纸张垃圾数据、海洋生物和海底垃圾同框数据、海底探索仪器和海底垃圾同框数据、海…...

如何进行Java程序的性能优化
在软件开发中,性能优化是一个至关重要的环节,它直接影响到用户体验、系统稳定性和资源消耗。对于Java程序而言,性能优化更是不可或缺的一部分。下面,我将从技术难点、面试官关注点、回答吸引力和代码举例四个方面,详细…...

Echarts柱状图数据太多,自定义长度之后,自适应浏览器缩放
不知道是不是最优解,但是当前解决了我遇到的问题,如有更好的方法,希望看到这篇文章的同学可以不吝指导一番,非常感谢 1、问题描述: 因Ecahrts柱状图数据有时多有时少,所以在数据达到一定程度之后ÿ…...

小白级教程—安装Ubuntu 20.04 LTS服务器
下载 本教程将使用20.04版进行教学 由于官方速度可能有点慢,可以下方的使用清华镜像下载 https://mirrors.tuna.tsinghua.edu.cn/ubuntu-releases/ 点击20.24版本 选择 ubuntu-20.04.6-live-server-amd64.iso 新建虚拟机 下载好后 我们使用 VMware 打开它 这里选…...

9、中华人民共和国个人信息保护法
第一章 总 则 第一条 为了保护个人信息权益,规范个人信息处理活动,促进个人信息合理利用,根据宪法,制定本法。 第二条 自然人的个人信息受法律保护,任何组织、个人不得侵害自然人的个人信息权益。 第三条 在中华人民共和国境内处理自然人个人信息的活动,适用本…...

经典回归模型及Python实现方法
文章目录 1. 引言2. 经典回归模型及Python实现2.1 线性回归 Linear Regression2.2 多项式回归 Polynomial Regression2.3 逻辑回归 Logistic Regression2.4 岭回归 Ridge Regression2.5 套索回归 LASSO Regression2.6 弹性网络回归 Elastic Net2.7 决策树回归 Decision Tree Re…...

Git 保留空文件夹结构
假设有如下 helloworld 项目结构: helloworld|--.git|--.gitignore|--Builds|--WebGL|--iOS|--Android现在有个需求,在上传到 github 仓库时,只想保留 WebGL、iOS、Android 文件夹的结构,不想要里面的内容,可以按以下…...

【吊打面试官系列】MySQL 中有哪几种锁?
大家好,我是锋哥。今天分享关于 【MySQL 中有哪几种锁?】面试题,希望对大家有帮助; MySQL 中有哪几种锁? 1、表级锁:开销小,加锁快;不会出现死锁;锁定粒度大,…...

小巧、免费高级分类整理桌面图标和文件程序
一、简介 1、专为Windows操作系统设计的桌面整理工具,旨在帮助用户更好地管理和整理桌面上的图标和文件。这款软件以其小巧、免费且无广告的特点受到用户的欢迎,尤其适合那些希望保持桌面整洁、提高工作效率的用户。 二、下载 1、下载地址: 官网链接:https://www.coodesker…...

Elasticsearch挂掉后,如何快速恢复数据
目录 一、Elasticsearch使用 二、实体类 2.1 mysql 实体类 2.2 Elasticsearch实体类 三、XXL-job定时执行 一、Elasticsearch使用 当我们做搜索功能时,如果为了提高查询效率,通常使用Elasticsearch搜索引擎加快搜索效率。以搜索商品为例,我…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...
