CPASSOC代码详解
加载环境
library("MASS")
require(MASS)
# Modern Applied Statistics with S,"S"指的是S语言,由贝尔实验室的约翰·钱伯斯(John Chambers)等人开发。S语言是R语言的前身,许多R语言的语法和功能都继承自S语言。
library("Matrix")
# Matrix包提供了用于处理稀疏和密集矩阵的函数。它可以高效地执行线性代数操作,比如计算矩阵的逆、求特征值等
# require(compiler)
# 使用require是因为它并不是必需的。如果你不使用compiler包,代码仍然可以正常运行。使用compiler包的目的是为了通过JIT(Just-In-Time)编译来提高代码的执行速度,特别是在处理大量循环或复杂计算时。
# enableJIT(4)
# 这是compiler的函数。这行代码启用JIT编译器,并设置为最高级别(4),即编译所有代码。这可以显著提高代码的执行速度。
计算未截断的检验分数
Non_Trucated_TestScore <- function(X, SampleSize, CorrMatrix)
{Wi = matrix(SampleSize, nrow = 1);sumW = sqrt(sum(Wi^2));W = Wi / sumW;Sigma = ginv(CorrMatrix);XX = apply(X, 1, function(x) {x1 <- matrix(x, ncol = length(x), nrow = 1); T = W %*% Sigma %*% t(x1);T = (T*T) / (W %*% Sigma %*% t(W));return(T[1,1]);} ); return(XX);
}
SHom <- cmpfun(Non_Trucated_TestScore);
函数参数:
X: 一个矩阵,表示样本数据。X是一个M×K的矩阵,其中M是SNP的数量,K是要组合的汇总统计量的数量。矩阵的每一列包含一个性状的M个SNP的汇总统计量。如果在一个队列中分析了多个性状,每个性状的汇总统计量将放在一列中。矩阵的每一行代表一个SNP。SampleSize: 样本大小。SampleSize是一个长度为M的向量,包含了用于获得K个汇总统计量的M个样本量。当前版本假设不同SNP的样本量是相同的。SampleSize用于在组合汇总统计量时作为权重。CorrMatrix: 相关矩阵。CorrMatrix是X矩阵列之间的相关矩阵,是一个K×K的矩阵,其中K是汇总统计量的数量。。如果X矩阵中没有缺失值,可以通过调用R函数cor(X)来获得CorrMatrix。如果X中有缺失值,可以在删除具有缺失汇总统计量的SNP后以相同方式计算CorrMatrix。对于GWAS数据,这个过程对估计相关矩阵的影响很小。
函数的主要步骤如下:
- 计算权重
W,并对其进行归一化。 - 计算相关矩阵的广义逆矩阵
Sigma。 - 对每一行数据
x进行处理:- 将
x转换为矩阵x1。 - 计算检验分数
T。
- 将
- 返回每一行数据的检验分数。
用公式来表达:
-
计算权重
W:
W = W i ∑ W i 2 W = \frac{Wi}{\sqrt{\sum Wi^2}} W=∑Wi2Wi -
计算相关矩阵的广义逆矩阵
Sigma:
Σ = ginv ( CorrMatrix ) \Sigma = \text{ginv}(\text{CorrMatrix}) Σ=ginv(CorrMatrix) -
对每一行数据
x,计算检验分数T:
x 1 = matrix ( x , ncol = length ( x ) , nrow = 1 ) x1 = \text{matrix}(x, \text{ncol} = \text{length}(x), \text{nrow} = 1) x1=matrix(x,ncol=length(x),nrow=1)
T = W ⋅ Σ ⋅ x 1 T T = W \cdot \Sigma \cdot x1^T T=W⋅Σ⋅x1T
T = ( T ⋅ T ) W ⋅ Σ ⋅ W T T = \frac{(T \cdot T)}{W \cdot \Sigma \cdot W^T} T=W⋅Σ⋅WT(T⋅T) -
返回每一行数据的检验分数
T[1,1]。
最终返回所有行的检验分数。
计算截断的检验分数
# X:矩阵,每行表示一个SNP(M),每列表示一个变量(K)
# SampleSize:样本大小向量
# CorrMatrix:相关矩阵
# correct:是否校正权重flag,默认值为1
# startCutoff:截断起始值,默认为0
# endCutoff:截断结束值,默认为1
# CutoffStep:截断步长,默认值为0.05
# isAllpossible:是否使用所有可能的截断值,默认为TRUETrucated_TestScore <- function(X, SampleSize, CorrMatrix, correct = 1, startCutoff = 0, endCutoff = 1, CutoffStep = 0.05, isAllpossible = T)
{N = dim(X)[2];Wi = matrix(SampleSize, nrow = 1);sumW = sqrt(sum(Wi^2));W = Wi / sumW; XX = apply(X, 1, function(x) {TTT = -1;if (isAllpossible == T ) {cutoff = sort(unique(abs(x))); ## it will filter out any of them. } else {cutoff = seq(startCutoff, endCutoff, CutoffStep); }for (threshold in cutoff) {x1 = x;index = which(abs(x1) < threshold);if (length(index) == N) break;A = CorrMatrix;W1 = W; if (length(index) !=0 ) { x1 = x1[-index]; A = A[-index, -index]; ## update the matrixW1 = W[-index]; }if (correct == 1){index = which(x1 < 0);if (length(index) != 0) {W1[index] = -W1[index]; ## update the sign}}A = ginv(A);x1 = matrix(x1, nrow = 1); W1 = matrix(W1, nrow = 1);T = W1 %*% A %*% t(x1);T = (T*T) / (W1 %*% A %*% t(W1));if (TTT < T[1,1]) TTT = T[1,1]; }return(TTT);} ); return(XX);
}
SHet <- cmpfun(Trucated_TestScore);
函数参数:
X: 一个矩阵,表示样本数据。SampleSize: 样本大小。CorrMatrix: 相关矩阵。correct: 一个布尔值,默认为1,表示是否需要修正符号。startCutoff: 截断的起始值,默认为0。endCutoff: 截断的结束值,默认为1。CutoffStep: 截断步长,默认为0.05。isAllpossible: 一个布尔值,默认为T,表示是否使用所有可能的截断值。
函数的主要步骤如下:
- 计算权重
W,并对其进行归一化。 - 对每一行数据
x进行处理:- 如果
isAllpossible为T,则计算所有可能的截断值cutoff。 - 否则,生成从
startCutoff到endCutoff的序列作为截断值。
- 如果
- 对每一个截断值
threshold:- 更新数据
x1和相关矩阵A,去除小于threshold的元素。 - 如果
correct为1,修正符号。 - 计算截断检验分数
T,并更新最大值TTT。
- 更新数据
- 返回每一行数据的最大截断检验分数。
用公式来表达:
-
计算权重
W:
W = W i ∑ W i 2 W = \frac{Wi}{\sqrt{\sum Wi^2}} W=∑Wi2Wi -
对每一行数据
x,计算截断值cutoff:
cutoff = { sort(unique(abs(x))) if isAllpossible = T seq(startCutoff, endCutoff, CutoffStep) otherwise \text{cutoff} = \begin{cases} \text{sort(unique(abs(x)))} & \text{if } \text{isAllpossible} = T \\ \text{seq(startCutoff, endCutoff, CutoffStep)} & \text{otherwise} \end{cases} cutoff={sort(unique(abs(x)))seq(startCutoff, endCutoff, CutoffStep)if isAllpossible=Totherwise -
对每一个截断值
threshold,更新数据x1和相关矩阵A:
x 1 = x (remove elements where ∣ x 1 ∣ < threshold ) x1 = x \quad \text{(remove elements where } |x1| < \text{threshold}) x1=x(remove elements where ∣x1∣<threshold)
A = CorrMatrix (remove corresponding rows and columns) A = \text{CorrMatrix} \quad \text{(remove corresponding rows and columns)} A=CorrMatrix(remove corresponding rows and columns)
W 1 = W (remove corresponding elements) W1 = W \quad \text{(remove corresponding elements)} W1=W(remove corresponding elements) -
如果
correct为1,修正符号:
W 1 [ index ] = − W 1 [ index ] (where x 1 < 0 ) W1[\text{index}] = -W1[\text{index}] \quad \text{(where } x1 < 0) W1[index]=−W1[index](where x1<0) -
计算截断检验分数
T:
A = ginv ( A ) A = \text{ginv}(A) A=ginv(A)
x 1 = matrix ( x 1 , n r o w = 1 ) x1 = \text{matrix}(x1, nrow = 1) x1=matrix(x1,nrow=1)
W 1 = matrix ( W 1 , n r o w = 1 ) W1 = \text{matrix}(W1, nrow = 1) W1=matrix(W1,nrow=1)
T = ( W 1 ⋅ A ⋅ x 1 T ) 2 W 1 ⋅ A ⋅ W 1 T T = \frac{(W1 \cdot A \cdot x1^T)^2}{W1 \cdot A \cdot W1^T} T=W1⋅A⋅W1T(W1⋅A⋅x1T)2 -
返回每一行数据的最大截断检验分数
TTT:
T T T = max ( T ) TTT = \max(T) TTT=max(T)
最终返回所有行的最大截断检验分数。
估计Gamma分布的参数
EstimateGamma <- function (N = 1E6, SampleSize, CorrMatrix, correct = 1, startCutoff = 0, endCutoff = 1, CutoffStep = 0.05, isAllpossible = T) {Wi = matrix(SampleSize, nrow = 1); sumW = sqrt(sum(Wi^2));W = Wi / sumW;Permutation = mvrnorm(n = N, mu = c(rep(0, length(SampleSize))), Sigma = CorrMatrix, tol = 1e-8, empirical = F);Stat = Trucated_TestScore(X = Permutation, SampleSize = SampleSize, CorrMatrix = CorrMatrix, correct = correct, startCutoff = startCutoff, endCutoff = endCutoff, CutoffStep = CutoffStep, isAllpossible = isAllpossible);a = min(Stat)*3/4ex3 = mean(Stat*Stat*Stat)V = var(Stat);for (i in 1:100){E = mean(Stat)-a;k = E^2/Vtheta = V/Ea = (-3*k*(k+1)*theta**2+sqrt(9*k**2*(k+1)**2*theta**4-12*k*theta*(k*(k+1)*(k+2)*theta**3-ex3)))/6/k/theta}para = c(k,theta,a);return(para);
}
函数参数:
N: 生成的样本数量,默认为1E6。SampleSize: 样本大小。CorrMatrix: 相关矩阵。correct: 一个布尔值,默认为1,表示是否需要修正符号。startCutoff: 截断的起始值,默认为0。endCutoff: 截断的结束值,默认为1。CutoffStep: 截断步长,默认为0.05。isAllpossible: 一个布尔值,默认为T,表示是否使用所有可能的截断值。
函数的主要步骤如下:
- 计算权重
W,并对其进行归一化。 - 生成
N个服从多元正态分布的随机样本Permutation。 - 使用
Trucated_TestScore函数计算截断检验分数Stat。 - 计算初始参数
a、ex3和V。 - 通过迭代更新参数
a,并计算Gamma分布的参数k和theta。 - 返回参数
k、theta和a。
用公式来表达:
-
计算权重
W:
W = W i ∑ W i 2 W = \frac{Wi}{\sqrt{\sum Wi^2}} W=∑Wi2Wi -
生成
N个服从多元正态分布的随机样本Permutation:
Permutation = mvrnorm ( n = N , μ = 0 , Σ = CorrMatrix ) \text{Permutation} = \text{mvrnorm}(n = N, \mu = \mathbf{0}, \Sigma = \text{CorrMatrix}) Permutation=mvrnorm(n=N,μ=0,Σ=CorrMatrix) -
使用
Trucated_TestScore函数计算截断检验分数Stat:
Stat = Trucated_TestScore ( X = Permutation , SampleSize = SampleSize , CorrMatrix = CorrMatrix , correct = correct , startCutoff = startCutoff , endCutoff = endCutoff , CutoffStep = CutoffStep , isAllpossible = isAllpossible ) \text{Stat} = \text{Trucated\_TestScore}(X = \text{Permutation}, \text{SampleSize} = \text{SampleSize}, \text{CorrMatrix} = \text{CorrMatrix}, \text{correct} = \text{correct}, \text{startCutoff} = \text{startCutoff}, \text{endCutoff} = \text{endCutoff}, \text{CutoffStep} = \text{CutoffStep}, \text{isAllpossible} = \text{isAllpossible}) Stat=Trucated_TestScore(X=Permutation,SampleSize=SampleSize,CorrMatrix=CorrMatrix,correct=correct,startCutoff=startCutoff,endCutoff=endCutoff,CutoffStep=CutoffStep,isAllpossible=isAllpossible) -
计算初始参数
a、ex3和V:
a = 3 4 min ( Stat ) a = \frac{3}{4} \min(\text{Stat}) a=43min(Stat)
ex3 = mean ( Stat 3 ) \text{ex3} = \text{mean}(\text{Stat}^3) ex3=mean(Stat3)
V = var ( Stat ) V = \text{var}(\text{Stat}) V=var(Stat) -
通过迭代更新参数
a,并计算Gamma分布的参数k和theta:
for i in 1 : 100 do \text{for } i \text{ in } 1:100 \text{ do} for i in 1:100 do
E = mean ( Stat ) − a E = \text{mean}(\text{Stat}) - a E=mean(Stat)−a
k = E 2 V k = \frac{E^2}{V} k=VE2
θ = V E \theta = \frac{V}{E} θ=EV
a = − 3 k ( k + 1 ) θ 2 + 9 k 2 ( k + 1 ) 2 θ 4 − 12 k θ ( k ( k + 1 ) ( k + 2 ) θ 3 − ex3 ) 6 k θ a = \frac{-3k(k+1)\theta^2 + \sqrt{9k^2(k+1)^2\theta^4 - 12k\theta(k(k+1)(k+2)\theta^3 - \text{ex3})}}{6k\theta} a=6kθ−3k(k+1)θ2+9k2(k+1)2θ4−12kθ(k(k+1)(k+2)θ3−ex3) -
返回参数
k、theta和a:
para = ( k , θ , a ) \text{para} = (k, \theta, a) para=(k,θ,a)
最终返回所有行的检验分数。
计算经验分布
# N:模拟次数,默认值为1E6,即100,000
# 其它参数与 Trucated_TestScore 相同EmpDist <- function (N = 1E6, SampleSize, CorrMatrix, correct = 1, startCutoff = 0, endCutoff = 1, CutoffStep = 0.05, isAllpossible = T) {Wi = matrix(SampleSize, nrow = 1); sumW = sqrt(sum(Wi^2));W = Wi / sumW;Permutation = mvrnorm(n = N, mu = c(rep(0, length(SampleSize))), Sigma = CorrMatrix, tol = 1e-8, empirical = F);Stat = Trucated_TestScore(X = Permutation, SampleSize = SampleSize, CorrMatrix = CorrMatrix, correct = correct, startCutoff = startCutoff, endCutoff = endCutoff, CutoffStep = CutoffStep, isAllpossible = isAllpossible);return(Stat);
}
函数参数:
N: 生成的样本数量,默认为1,000,000。SampleSize: 样本大小。CorrMatrix: 相关矩阵。correct: 一个布尔值,默认为1,表示是否需要修正符号。startCutoff: 截断的起始值,默认为0。endCutoff: 截断的结束值,默认为1。CutoffStep: 截断步长,默认为0.05。isAllpossible: 一个布尔值,默认为T,表示是否使用所有可能的截断值。
函数的主要步骤如下:
- 计算权重
W,并对其进行归一化。 - 使用多元正态分布生成
N个样本,均值为0,协方差矩阵为CorrMatrix。 - 调用
Trucated_TestScore函数计算截断检验分数。 - 返回计算得到的统计量
Stat。
用公式来表达:
-
计算权重
W:
W = W i ∑ W i 2 W = \frac{Wi}{\sqrt{\sum Wi^2}} W=∑Wi2Wi -
使用多元正态分布生成
N个样本:
Permutation = mvrnorm ( n = N , μ = 0 , Σ = CorrMatrix ) \text{Permutation} = \text{mvrnorm}(n = N, \mu = \mathbf{0}, \Sigma = \text{CorrMatrix}) Permutation=mvrnorm(n=N,μ=0,Σ=CorrMatrix) -
调用
Trucated_TestScore函数计算截断检验分数:
Stat = Trucated_TestScore ( X = Permutation , SampleSize = SampleSize , CorrMatrix = CorrMatrix , correct = correct , startCutoff = startCutoff , endCutoff = endCutoff , CutoffStep = CutoffStep , isAllpossible = isAllpossible ) \text{Stat} = \text{Trucated\_TestScore}(X = \text{Permutation}, \text{SampleSize} = \text{SampleSize}, \text{CorrMatrix} = \text{CorrMatrix}, \text{correct} = \text{correct}, \text{startCutoff} = \text{startCutoff}, \text{endCutoff} = \text{endCutoff}, \text{CutoffStep} = \text{CutoffStep}, \text{isAllpossible} = \text{isAllpossible}) Stat=Trucated_TestScore(X=Permutation,SampleSize=SampleSize,CorrMatrix=CorrMatrix,correct=correct,startCutoff=startCutoff,endCutoff=endCutoff,CutoffStep=CutoffStep,isAllpossible=isAllpossible) -
返回统计量
Stat。
相关文章:

CPASSOC代码详解
加载环境 library("MASS") require(MASS) # Modern Applied Statistics with S,"S"指的是S语言,由贝尔实验室的约翰钱伯斯(John Chambers)等人开发。S语言是R语言的前身,许多R语言的语法和功能都…...
dirfuzz-web敏感目录文件扫描工具
dirfuzz介绍 dirfuzz是一款基于Python3的敏感目录文件扫描工具,借鉴了dirsearch的思路,扬长避短。在根据自身实战经验的基础上而编写的一款工具,经过断断续续几个月的测试、修改和完善。 项目地址:https://github.com/ssrc-c/di…...
计算机发展史 | 从起源到现代技术的演进
computer | Evolution from origins to modern technology 今天没有参考资料哈哈 PPT:(评论区?) 早期计算工具 算盘 -算盘是一种手动操作的计算辅助工具,起源于中国,迄今已有2600多年的历史,是…...
45-3 护网溯源 - 为什么要做溯源工作
官网:CVERC-国家计算机病毒应急处理中心 西工大遭网络攻击再曝细节!13名攻击者身份查明→ (baidu.com) 护网溯源是指通过技术手段追踪网络攻击的来源和行为,其重要性体现在以下几个方面: 安全防御:了解攻击源头可以帮助组织加强网络安全防御,及时采取措施防止攻击的再次…...

【JavaEE 进阶(二)】Spring MVC(下)
❣博主主页: 33的博客❣ ▶️文章专栏分类:JavaEE◀️ 🚚我的代码仓库: 33的代码仓库🚚 🫵🫵🫵关注我带你了解更多进阶知识 目录 1.前言2.响应2.1返回静态界面2.2返回数据2.3返回HTML代码 3.综合练习3.1计算器3.2用户登…...

光波长 深入程度
UV深入程度(UVC, UVB, UVA)https://mp.weixin.qq.com/s?__bizMzkwNTM0Njk3MA&mid2247483934&idx1&sn92d1ba67ead404e7714af11ec0526786&chksmc0f868ebf78fe1fd0610493e6f49a5d90835a20a829a900746906cda12f2fa12…...

MySQL数据库常见工具的基础使用_1
在上一篇文章中提到了对MySQL数据库进行操作的一些常见工具 mysqlcheck mysqlcheck是一个用于数据库表的检查,修复,分析和优化的一个客户端程序 分析的作用是查看表的关键字分布,能够让sql生成正确的执行计划(支持InnoDB,MyISAM,NDB)检查的作用是检查…...

C语言中指针的说明
什么是指针? 在C语言当中,我们可以将指针理解为内存当中存储的地址,就像生活当中,一个小区里面,在小区里面有很单元,每一栋单元,单元内的房间有着不同的房间号,我们可以同过几栋几单…...

webrtc vp8/9视频编解码介绍
文章目录 一、libvpx项目介绍libvpx基本概念编码器使用流程解码器使用流程示例代码:官方文档和资源二、VP8/9在WebRTC中的应用2.1 VP82.2 VP92.3如何选择哪种编码方式2.4 vp9编码的主要步骤2.5 vp9解码C++代码示例注意事项三、webrtc在音视频传输中是怎样选择vp8还是vp9<...

【机器学习300问】107、自然语言处理(NLP)领域有哪些子任务?
自然语言处理(NLP)是计算机科学、人工智能和语言学领域的一个交叉学科,致力于让计算机能够理解、解析、生成和与人类的自然语言进行互动。自然语言指的是人们日常交流使用的语言,如英语、汉语等,与计算机编程语言相对。…...

面试被问准备多久要孩子?这样回答
听说有人面试被问到多久要孩子的问题,当时觉得很尴尬,不知如何回答,怕回答的不好不被录用,其实你可以这样回答,让面试官心满意足。 A 面试官:结婚了吗? 我:结婚了 面试官࿱…...
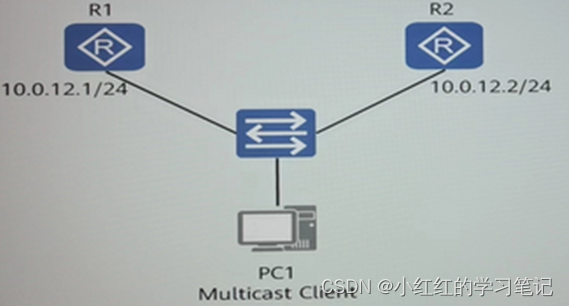
HCIP-Datacom-ARST自选题库__多种协议简答【11道题】
1.BGP/MPLSIP VPN的典型组网场景如图所示,PE1和PE2通过LoopbackO建立MP-IBGP,PE1和PE2之间只传递VPN路由,其中PE1BGP进程的部分配置已在图中标出,则编号为0的命令不是必须的。(填写阿拉伯数字) 3 2.在如图所示的Hub&Spok…...
C# 泛型函数
1.非约束 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace MyGeneirc {public class GeneircMethod{/// <summary>/// 泛型方法解决,一个方法,满足不同参数类型…...
C# Onnx E2Pose人体关键点检测
C# Onnx E2Pose人体关键点检测 目录 效果 模型信息 项目 代码 下载 效果 模型信息 Inputs ------------------------- name:inputimg tensor:Float[1, 3, 512, 512] --------------------------------------------------------------- Outputs ---…...

YOLO10:手把手安装教程与使用说明
目录 前言一、YOLO10检测模型二、YOLO安装过程1.新建conda的环境 yolo10安装依赖包测试 总结 前言 v9还没整明白,v10又来了。而且还是打败天下无敌手的存在,连最近很火的RT-DETR都被打败了。那么,笑傲目标检测之林的v10又能持续多久呢&#…...

EasyRecovery2024永久免费crack激活码注册码
在数字化时代,数据已经成为我们生活和工作中不可或缺的一部分。无论是个人用户还是企业用户,都面临着数据丢失的风险。一旦数据丢失,可能会给我们的工作带来极大的不便,甚至可能对企业造成重大损失。因此,数据安全和恢…...

Linux Centos内网环境中安装mysql5.7详细安装过程
一、下载安装包 下载地址(可下载历史版本): https://downloads.mysql.com/archives/community 二、解压到安装路径 tar -zxvf mysql-5.7.20-linux-glibc2.12-x86_64.tar.gz三、重命名 mv /usr/local/mysql-5.7.20-linux-glibc2.12-x86_64 …...

新字符设备驱动实验学习
register_chrdev 和 unregister_chrdev 这两个函数是老版本驱动使用的函数,现在新的字符设备驱动已经不再使用这两个函数,而是使用Linux内核推荐的新字符设备驱动API函数。新字符设别驱动API函数在驱动模块加载的时候自动创建设备节点文件。 分配和释放…...

篇1:Mapbox Style Specification
目录 引言 地图创建与样式加载 Spec Reference Root sources type:vector矢量瓦片...

实时监控与报警:人员跌倒检测算法的实践
在全球范围内,跌倒事件对老年人和儿童的健康与安全构成了重大威胁。据统计,跌倒是老年人意外伤害和死亡的主要原因之一。开发人员跌倒检测算法的目的是通过技术手段及时发现和响应跌倒事件,减少因延迟救助而造成的严重后果。这不仅对老年人群…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...
