函数的概念及图像
注: 判断两函数是否相同,只看定义域和对应法则。
1. 函数的定义
一般的,在一个变化过程中有两个变量 x,y。如果对于x在某个变化范围内的每一个确定值,按照某个对应法则,都有唯一确定的值y和他对应。那么y就是x的函数,x叫做自变量,y叫做因变量。可以记作 y = f(x) 其中,f表示对应法则。
2. 函数的表示方法
- 解析法:用等式表示两个变量间函数关系的方法。如 y = 2x + 3;
- 列表法:用表格表示两个变量间函数关系的方法。
- 图像法:用图像表示两个变量间函数关系的方法。
3. 常见的函数定义域
- f(x) 是整数时,定义域是全体实数。
- f(x) 是分式函数时,分母不能为0。
- f(x) 是偶次方根时,被开方数大于等于0。若为奇次方根,则被开方数无要求。0的0次方无意义。
- 对数函数的真数大于0。
- 对数函数或指数函数的底数大于0且不等于1。
- 在y = tan x 中, x ≠ kΠ + Π/2 (k 属于Z)。
- 若是有几个式子构成的,则定义域为这几个式子定义域的交集。
4. 函数的单调性
1. 函数单调性的定义
在一个区间上,如果自变量X的任意两个值,x1、x2,当x1 < x2时,都有 f(x1) 小于 f(x2)那么称f(x)在此区间上是增函数;但若 f(x1) > f(x2),那么称该函数在此区间上是减函数。
如果函数y = f(x) 在某区间上是增函数/减函数,就说 f(x) 在此区间上具有单调性,在此区间叫做f(x)的单调区间。
2. 函数单调性的图像特征

3. 函数单调性的判断方法
- 设x1,x2是定义域活区间D上的任意两个值,且x1<x2。
- 做差 f(x1) - f(x2),并将差的形式化简,目标是有利于判断结果的正负号。
- 判断 f(x1) - f(x2) 的正负。
- 得出结论。
5. 函数的奇偶性
1.函数奇偶性的定义
设y = f(x),在其定义域内任取一点,且 -x 也在其定义域内。
- 若 f(x) = f(-x),则称函数f(x)为偶函数。
- 若 f(-x) = -f(x) 则成函数f(x)为奇函数。
2. 函数奇偶性的图像特征
- 奇函数的图像关于原点对称。
- 偶函数的图像关于y轴对称。
3. 奇偶性四则运算
- 奇函数 + 奇函数 = 奇函数
- 偶函数 + 偶函数 = 偶函数
- 奇函数 + 偶函数 = 非奇非偶函数
- 奇函数 * 奇函数 = 偶函数
- 偶函数 * 偶函数 = 偶函数
- 奇函数 * 偶函数 = 奇函数
相关文章:

函数的概念及图像
注: 判断两函数是否相同,只看定义域和对应法则。 1. 函数的定义 一般的,在一个变化过程中有两个变量 x,y。如果对于x在某个变化范围内的每一个确定值,按照某个对应法则,都有唯一确定的值y和他对应。那么y就…...
Linux中Apache网站基于Http服务的访问限制(基于地址/用户)
🏡作者主页:点击! 👨💻Linux高级管理专栏:点击! ⏰️创作时间:2024年6月3日11点44分 🀄️文章质量:95分 为了更好地控制对网站资源的访问,可…...

滚动条详解:跨平台iOS、Android、小程序滚动条隐藏及自定义样式综合指南
滚动条是用户界面中的图形化组件,用于指示和控制内容区域的可滚动范围。当元素内容超出其视窗边界时,滚动条提供可视化线索,并允许用户通过鼠标滚轮、触屏滑动或直接拖动滑块来浏览未显示部分,实现内容的上下或左右滚动。它在保持…...
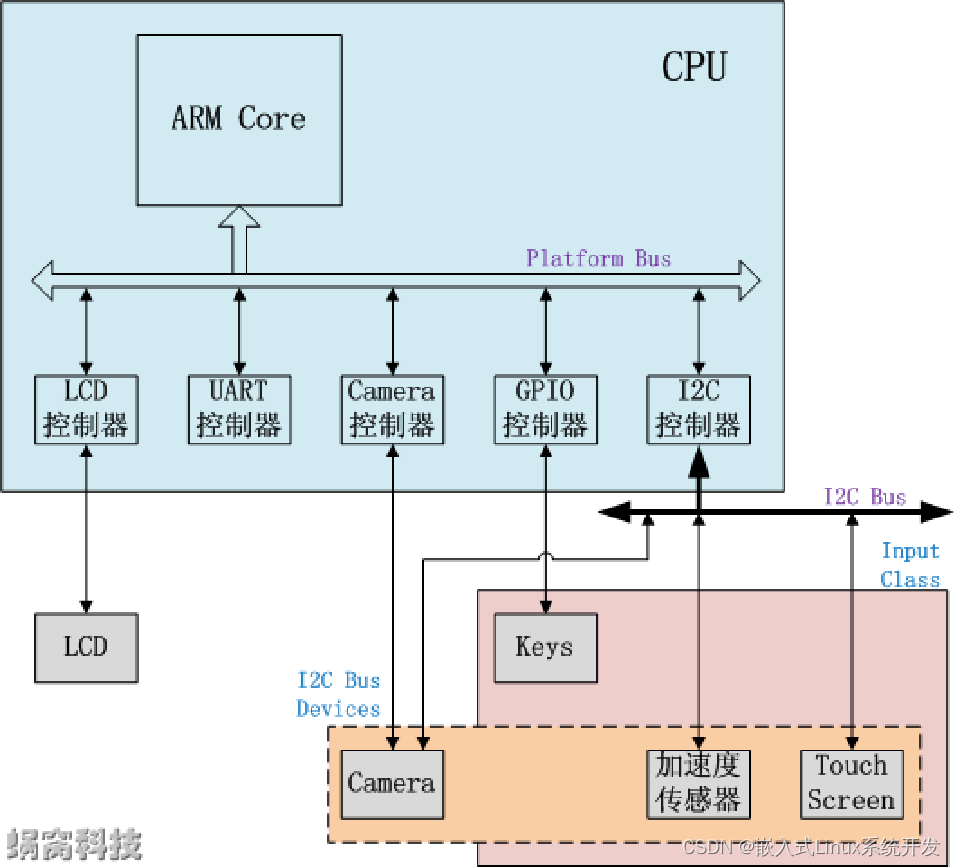
06 Linux 设备驱动模型
1、Overview Linux-2.6 引入的新的设备管理机制 - kobject 降低设备多样性带来的 Linux 驱动开发的复杂度,以及设备热拔插处理、电源管理等将硬件设备归纳、分类,然后抽象出一套标准的数据结构和接口驱动的开发,就简化为对内核所规定的数据结构的填充和实现驱动模型是 Linu…...
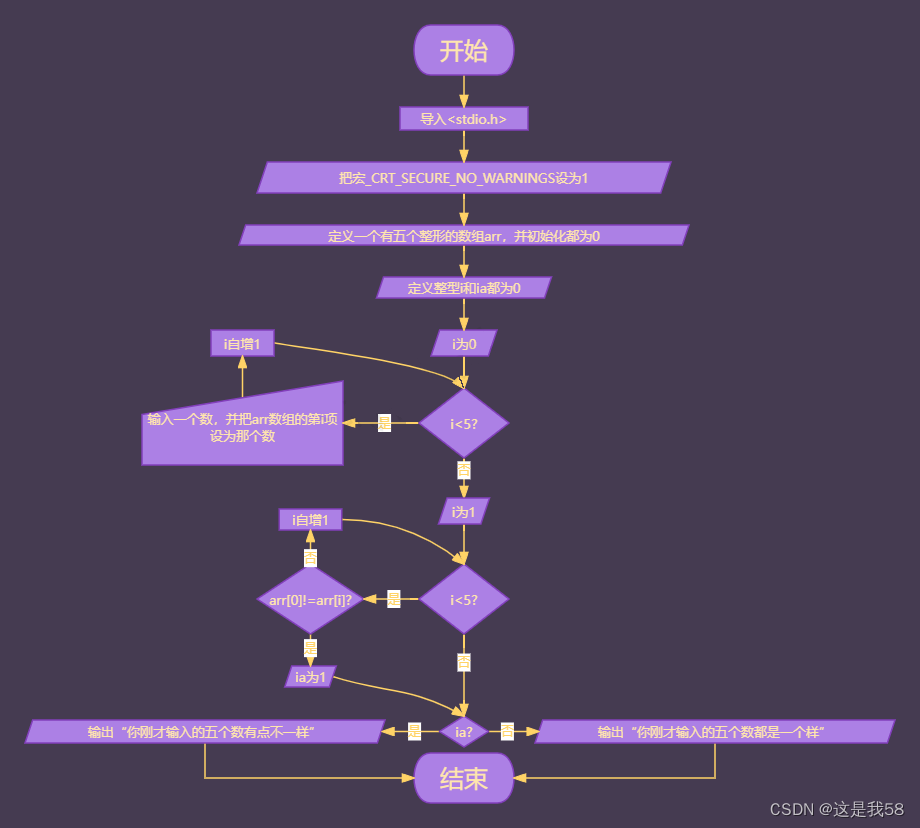
检测五个数是否一样的算法
目录 算法算法的输出与打印效果输出输入1输入2 打印打印1打印2 算法的流程图总结 算法 int main() {int arr[5] { 0 };int i 0;int ia 0;for (i 0; i < 5; i) { scanf("%d", &arr[i]); }for (i 1; i < 5; i) {if (arr[0] ! arr[i]) {ia 1;break;} }…...
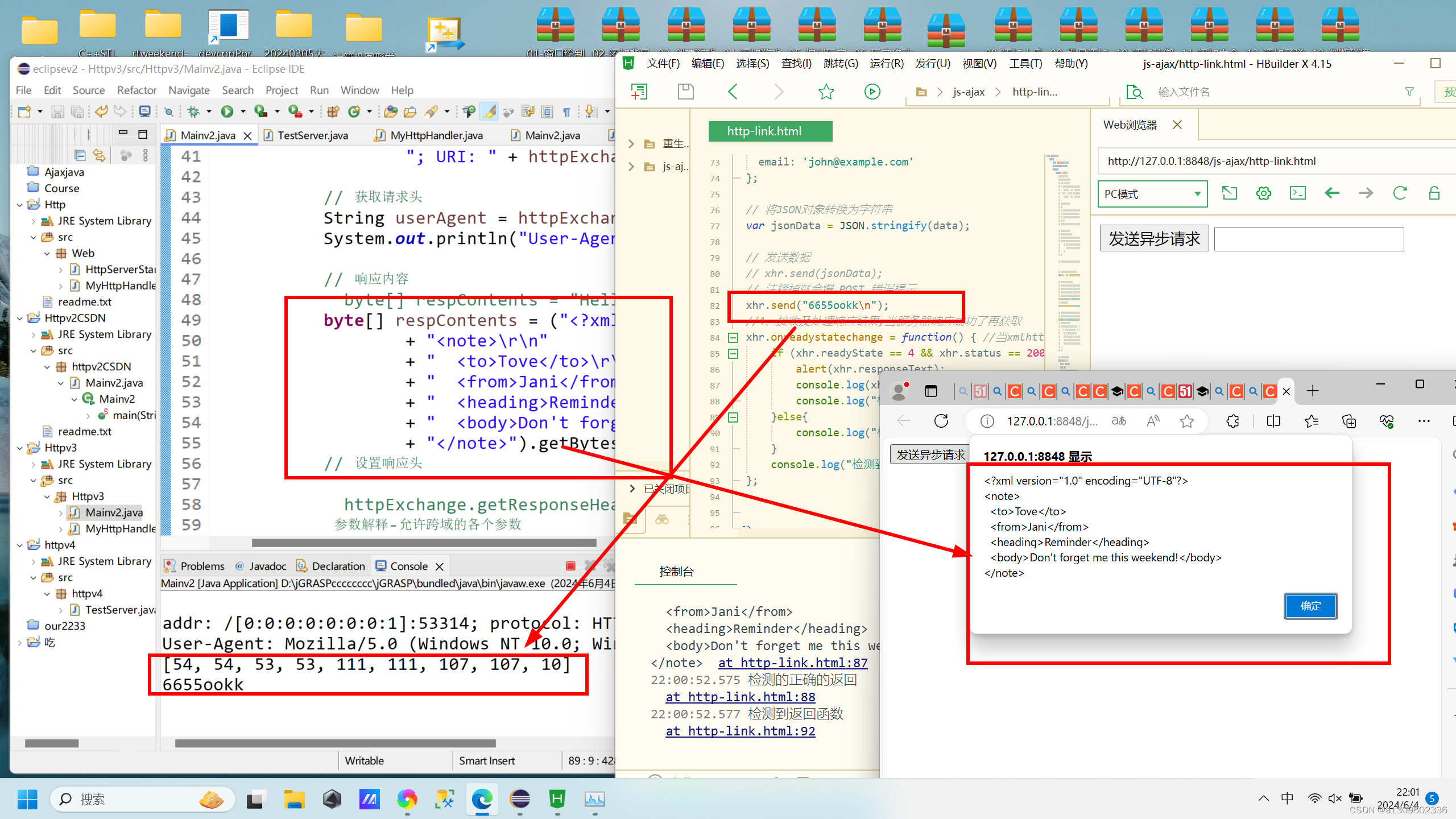
java 原生http服务器 测试JS前端ajax访问实现跨域传post数据
后端 java eclipse 字节流转字符 package Httpv3;import com.sun.net.httpserver.Headers; import com.sun.net.httpserver.HttpExchange; import com.sun.net.httpserver.HttpHandler; import com.sun.net.httpserver.HttpServer;import java.io.IOException; import java.i…...
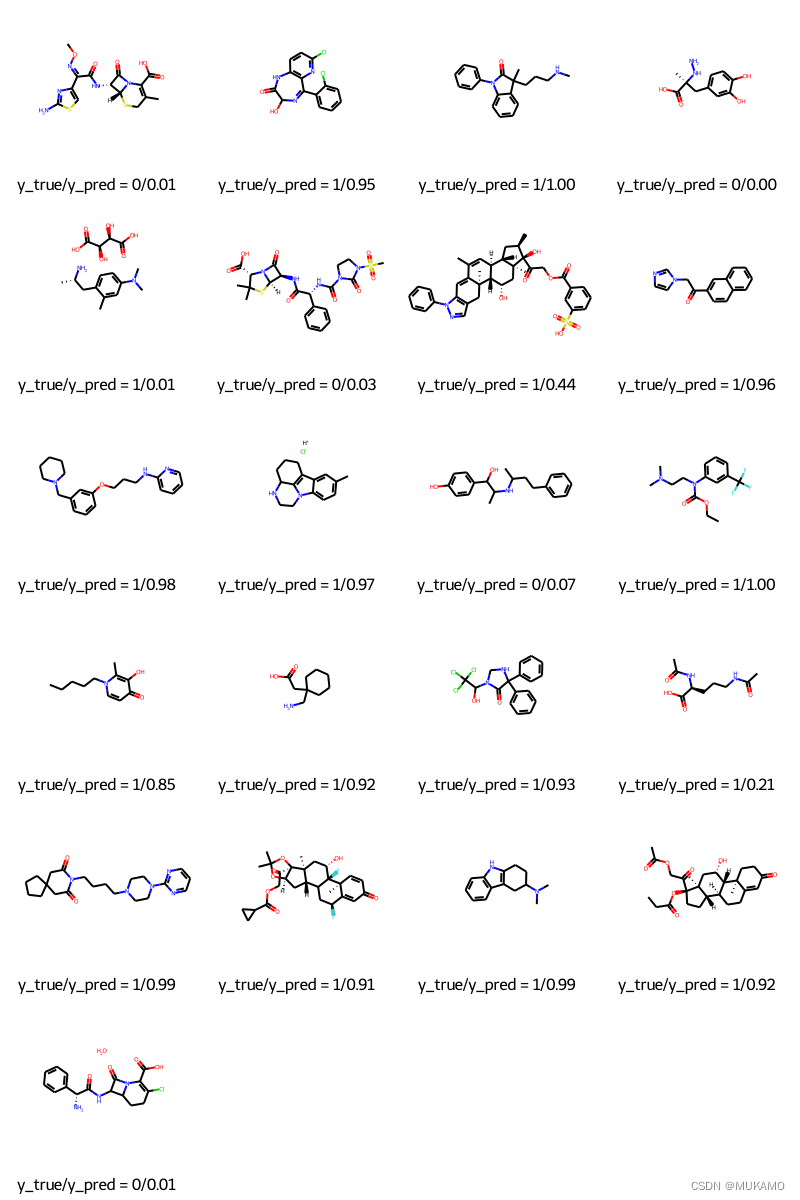
【机器学习】消息传递神经网络(MPNN)在分子预测领域的医学应用
1. 引言 1.1. 分子性质预测概述 分子性质预测是计算机辅助药物发现流程中至关重要的任务之一,它在许多下游应用如药物筛选和药物设计中发挥着核心作用: 1.1.1. 目的与重要性: 分子性质预测旨在通过分子内部信息(如原子坐标、原…...
Python Flask实现蓝图Blueprint配置和模块渲染
Python基础学习: Pyhton 语法基础Python 变量Python控制流Python 函数与类Python Exception处理Python 文件操作Python 日期与时间Python Socket的使用Python 模块Python 魔法方法与属性 Flask基础学习: Python中如何选择Web开发框架?Pyth…...

Vue10-事件修饰符
一、示例:<a>标签不执行默认的跳转行为 1-1、方式一 <a href"http://www.baidu.com" onclick"event.preventDefault();">点击我</a> 1-2、方式二 1-3、方式三:事件修饰符 二、Vue的六种事件修饰符 2-1、prevent&…...

oracle中如何查询特定日期?
1. select last_day(to_date(20230101,YYYYMMDD)) from dual; select last_day(to_date(V_END_DATE,YYYYMMDD)) from dual; --查询任意一天 当月的最后一天 2. select to_char(to_date(20230101,YYYYMMDD)-1,YYYYMMDD) INTO V_START_DATE FROM DUAL; select to_char(to_dat…...

Python使用rosbag使用getattr只能获取一层的数据,不能直接获取多层数据例如 a.b.c.d。使用for range写一个递归用来获取多层数据
使用for循环和range来遍历属性列表确实是一个更简单直观的方式,特别是不需要考虑性能优化和异常处理时。以下是使用for循环代替递归的示例代码: python def get_nested_attr(obj, attr_str): attrs attr_str.split(.) for attr in attrs: # 尝试获取下…...

LNWT--篇章三小测
问题1: BERT训练时候的学习率learning rate如何设置? 在训练初期使用较小的学习率(从 0 开始),在一定步数(比如 1000 步)内逐渐提高到正常大小(比如上面的 2e-5),避免模型过早进入…...

【NoSQL】Redis练习
1、redis的编译安装 systemctl stop firewalld systemctl disable firewalld setenforce 0 yum install -y gcc gcc-c make wget cd /opt wget https://download.redis.io/releases/redis-5.0.7.tar.gz tar zxvf redis-5.0.7.tar.gz -C /opt/cd /opt/redis-5.0.7/ # 编译 make…...

Git 和 Github 的使用
补充内容:EasyHPC - Git入门教程【笔记】 文章目录 常用命令配置信息分支管理管理仓库 概念理解SSH 密钥HTTPS 和 SSH 的区别在本地生成 SSH key在 Github 上添加 SSH key 使用的例子同步本地仓库的修改到远程仓库拉取远程仓库的修改到本地仓库拉取远程仓库的分支并…...

学习分享-断路器Hystrix与Sentinel的区别
断路器(Circuit Breaker)简介 断路器(Circuit Breaker)是一种用于保护分布式系统的服务稳定性和容错性的设计模式。它的主要作用是在检测到某个服务的调用出现故障(如超时、异常等)时,快速失败…...
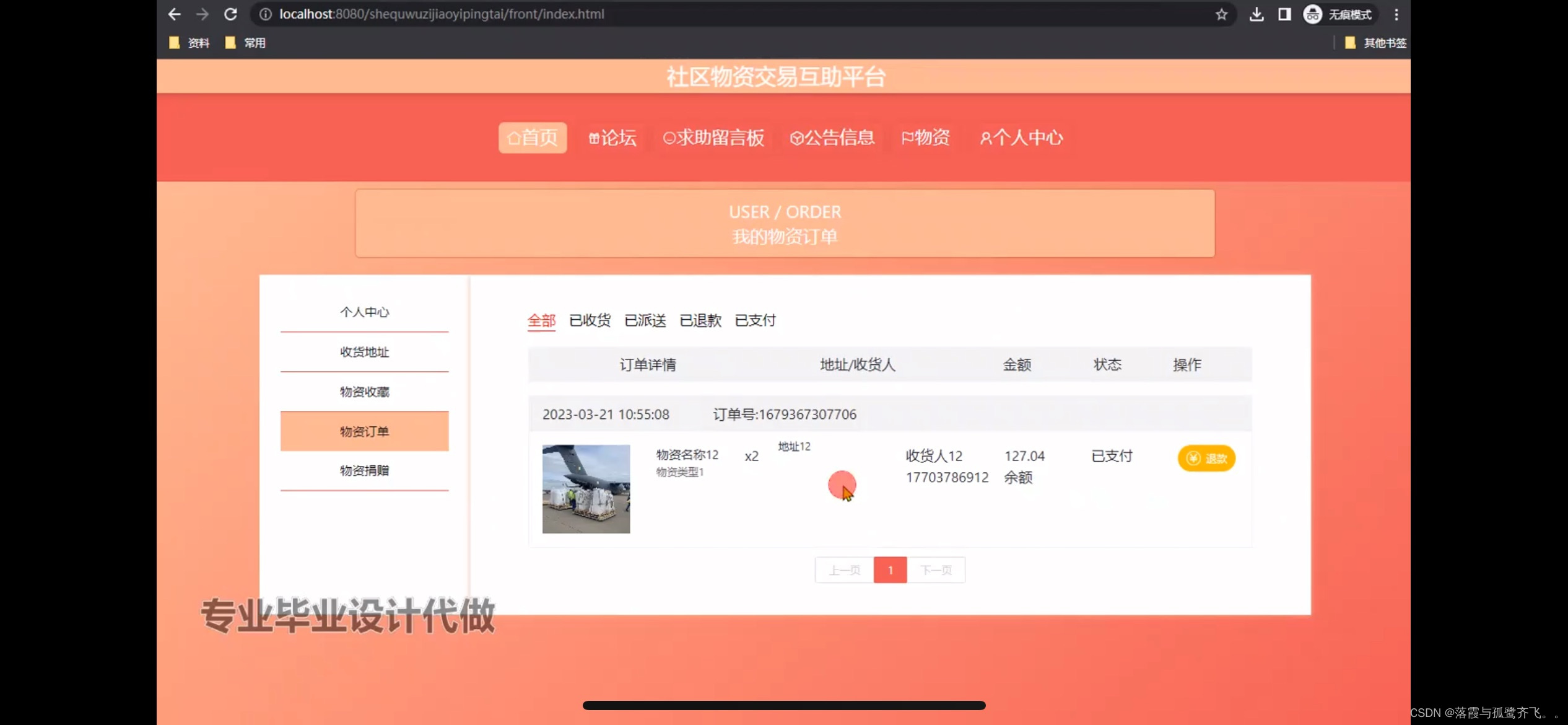
社区物资交易互助平台的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,基础数据管理,论坛管理,公告信息管理 前台账户功能包括:系统首页,个人中心,论坛,求助留言板,公…...

19-Nacos-服务实例的权重设置
19-Nacos-服务实例的权重设置 1.根据权重负载均衡: 1.服务器设备性能有差异,部分实例所在及其性能较高,有一些较差,我们希望性能好的机器承担更多的用户请求 Nacos提供了权重配置来控制访问频率,权重越大则访问频率…...

R语言数据探索和分析23-公共物品问卷分析
第一次实验使用最基本的公共物品游戏,不外加其他的treatment。班里的学生4人一组,一共44/411组。一共玩20个回合的公共物品游戏。每回合给15秒做决定的时间。第十回合后,给大家放一个几分钟的“爱心”视频(链接如下)&a…...

Webix前端界面框架:深度解析与应用实践
Webix前端界面框架:深度解析与应用实践 Webix,作为一款功能强大的前端界面框架,近年来在开发社区中逐渐崭露头角。本文将从四个方面、五个方面、六个方面和七个方面,深入剖析Webix的特性、优势、应用实践以及面临的挑战ÿ…...

Qt基于SQLite数据库的增删查改demo
一、效果展示 在Qt创建如图UI界面,主要包括“查询”、“添加”、“删除”、“更新”,四个功能模块。 查询:从数据库中查找所有数据的所有内容,并显示在左边的QListWidget控件上。 添加:在右边的QLineEdit标签上输入需…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
