算法竞赛一句话解题经典问题分析 ©ntsc 2024
原名:算法竞赛一句话解题&经典问题分析 ©ntsc 2024
处理进度
- 绿:P1381【~P(今日进度)】
- 蓝:P1099
致CSDN网友:
本文章不定期更新!文章链接:
经典问题分析
基础知识与编程环境
- 了解树的中序遍历的性质来设计算法→P1040
思维
-
考虑每一个数字的贡献而不是考虑每一种情况那个数字做贡献→mna.816/p4
-
观察数据访问,发现一个范围很小→将这个数据作为最外层循环,每次考虑这个数据取特定值时的答案的求解→P1311
-
求最优化一个计算式,并且里面有一个值需要你来确定,并且不好直接求→二分→优化每一次计算过程→O(n)求多个询问区间内>m的数字的个数之和→先把≤m的数字赋0,然后跑前缀和,再对每个询问O(1)处理→P1314
-
将字符串哈希后离散化→双指针,右端点不断扩散(右移),左端点贪心地缩小(右移)→P1381
STL 模板
排序算法
-
在DAG中,更新一个点的信息如果需要先更新其来点→拓扑排序→P1038
-
一些偏序问题(非计数类),考虑拓扑排序进行顺序确定→考虑不同情况反映在DAG中的情况→一定有序:存在n长链/错误:有环→P1347
搜索算法
-
O ( 2 40 ) O(2^{40}) O(240)的搜索→Meet in the middle
-
数据范围小的时候可以考虑直接搜索(填表)→P1004
-
有些时候看上去n不适合搜索(e.g. n=50),但是加上剪枝也许就是正解→剪枝优化时间复杂度的证明和计算→P1034
-
常见数矩阵个数优化(n4变n3)→P1191
-
结合计算性质进行剪枝→P1092
-
枚举→P1378
图论算法
-
应用分层图思想【模型】→P1073
-
记录附加信息的最短路→P1078,P1144
-
给定关系求层级数最小值→先整理出约束(e.g. A在B之上),连有向边→求最长链→拓扑排序→P1983
-
总结出最后的图的特点→生成树→最大生成树→证明某些很难解决的情况不存在→简单解决→P1265
线性结构
集合与森林
-
使用并查集额外维护集合信息→将集合信息统一整理至某一个集合的代表元素上去,注意清空过期的代表元素→P1196
-
断边维护连通块个数→化断边为加边→P1197
树形结构
-
维护树链上的信息→树上倍增,树剖
-
维护子树信息→dfn线段树
-
从题目中整理出树的性质→设计树形dp进行最优方案求解→P1131
-
结合数据范围,预估复杂度→搜索→设计搜索→因为每一层只能切断一个,所以就可以对每一个节点搜索其最优的切断方式(使用回溯的数据来贪心选择)→P1041
-
理清题意→整理出答案的几种来源/情况→对于每一种情况独立思考做法,最后组合起来→P1099←答案有两种情况:来自直径两端,来自最长的侧链。并且来自最长的侧链的那个答案只需要计算侧链端点到直径的距离即可。不需要考虑侧链+一部分直径的情况,因为如果这种情况可以作为答案,那么直径就要改了!
数据结构
-
动态维护数字序列信息→权值线段树→P1168
-
线段树模板→P1198,P1253
算法策略
- 维护4指针2区间信息→莫队,将4指针拆为2指针及多个询问→P5268
字符串算法 哈希表
动态规划
-
用“非法情况一定更劣”来消去需要考虑非法的情况→P1006
-
dp不就是枚举情况并选最优吗?→P1040
-
断环为链→P1043,P1063
-
题目中有明显的“合并”流程,则考虑区间dp→P1063
-
依赖背包嗯可以看成树形dp来做,如附件数量很少则可以枚举每个主件和附件的配对情况并作为一个物品的多种情况。当遇到一个物品有多个挡位时的背包问题也可以参考本题→P1064
-
从题目信息中构造出背包(f_{i,j})的物品(i)及两个维度(价值(f)和容量(j))→P1156,P1282
-
考虑树形dp并考虑复杂度→P1273
-
主要考验dp转移的设计以及dp优化→思维→P1070
-
一开始考虑贪心→给定方案计算答案很快→不好实现,所以使用搜索(计算每一种可行情况)→使用dp实现记忆化搜索→压维优化→P1284
-
期望dp→得出概率的计算式→使用dp求出计算式中的值并计算→本题:第i题对的概率=i-1题答案=i题答案→P1297
-
树形dp,最大权独立集→P1352
数学与其他
初等数学
-
总结出性质来优化枚举的复杂度→P1072
-
要勤于推导式子→推导后得出贪心算法而不是一开始选择dp→P1080
初等数论
-
扩展欧几里得变形与理解→P1082
-
矩阵乘法→P1349
离散与组合数学
线性代数
高等数学
最优化
-
博弈论→P1247
-
舞蹈链及其变形→P1074
计算几何
信息论
相关文章:

算法竞赛一句话解题经典问题分析 ©ntsc 2024
原名:算法竞赛一句话解题&经典问题分析 ©ntsc 2024 处理进度 绿:P1381【~P(今日进度)】蓝:P1099 致CSDN网友: 本文章不定期更新!文章链接: 经典问题分析 基础知识与编程…...

【TensorFlow深度学习】强化学习中的贝尔曼方程及其应用
强化学习中的贝尔曼方程及其应用 强化学习中的贝尔曼方程及其应用:理解与实战演练贝尔曼方程简介应用场景代码实例:使用Python实现贝尔曼方程求解状态价值结语 强化学习中的贝尔曼方程及其应用:理解与实战演练 在强化学习这一复杂而迷人的领…...

牛客 NC129 阶乘末尾0的数量【简单 基础数学 Java/Go/PHP/C++】
题目 题目链接: https://www.nowcoder.com/practice/aa03dff18376454c9d2e359163bf44b8 https://www.lintcode.com/problem/2 思路 Java代码 import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改ÿ…...

【Spring Boot】异常处理
异常处理 1.认识异常处理1.1 异常处理的必要性1.2 异常的分类1.3 如何处理异常1.3.1 捕获异常1.3.2 抛出异常1.3.4 自定义异常 1.4 Spring Boot 默认的异常处理 2.使用控制器通知3.自定义错误处理控制器3.1 自定义一个错误的处理控制器3.2 自定义业务异常类3.2.1 自定义异常类3…...

Laravel学习-自定义辅助函数
因为laravel框架的辅助函数helpers不会进入版本库,被版本库忽略的,只有自己创建一个helpers辅助函数。 可以在任意文件下创建helpers.php文件,建议在app目录下, 然后在composer.json文件中,autoload 中间,…...

LLVM Cpu0 新后端6
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
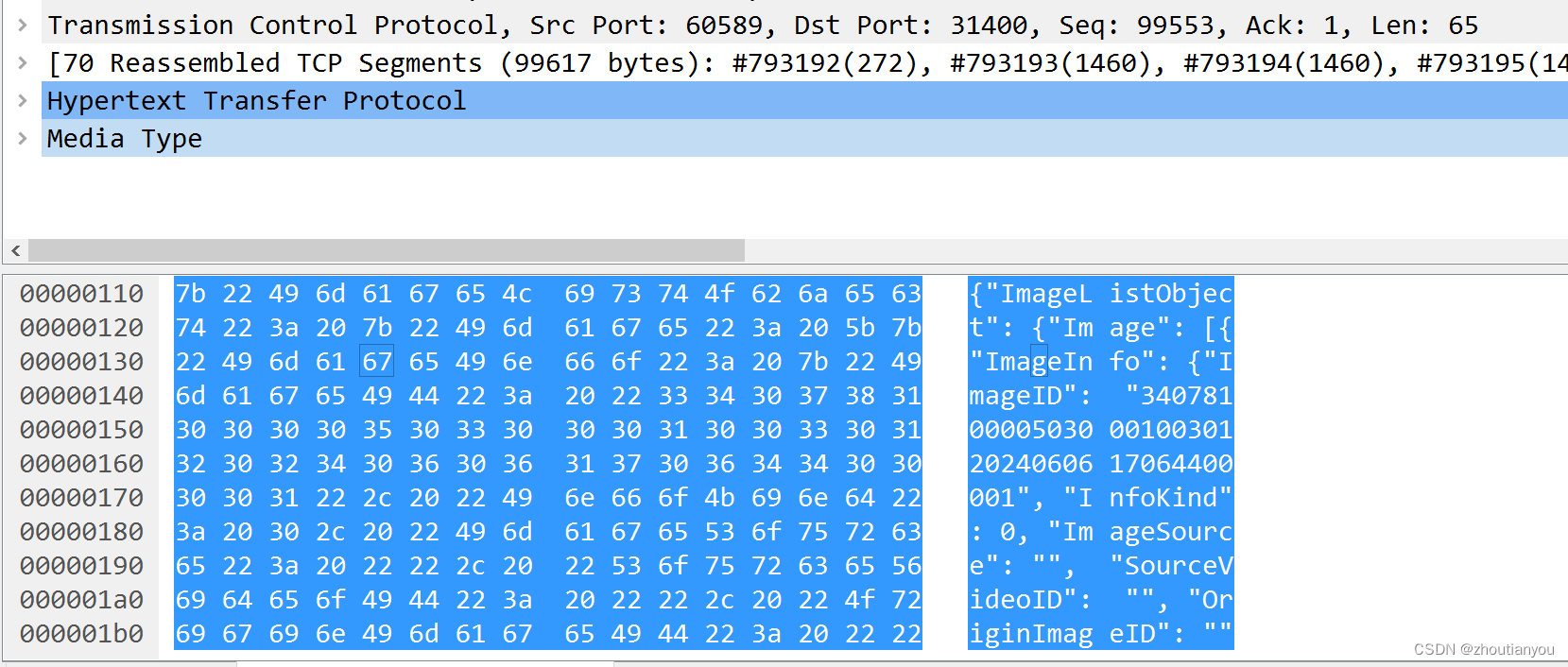
GAT1399协议分析(9)--图像上传
一、官方定义 二、wirechark实例 有前面查询的基础,这个接口相对简单很多。 请求: 文本化: POST /VIID/Images HTTP/1.1 Host: 10.0.201.56:31400 User-Agent: python-requests/2.32.3 Accept-Encoding: gzip, deflate Accept: */* Connection: keep-alive content-type:…...

Spring ApplicationContext的getBean方法
Spring ApplicationContext的getBean方法 在Spring框架的ApplicationContext中,getBean(Class<T> requiredType)方法可以接受一个类类型参数,这个参数可以是接口类也可以是实现类。 使用接口类: 如果requiredType是一个接口,…...
—— 自动摘要)
自然语言处理(NLP)—— 自动摘要
自动摘要是一种将长文本信息浓缩为短文本的技术,旨在保留原文的主要信息和意义。 1 自动摘要的第一种方法 它的第一种方法是基于理解的,受认知科学和人工智能的启发。 在这个方法中,我们首先建立文本的语义表示,这可以理解为文本…...

Spring RestClient报错:400 Bad Request : [no body]
我项目采用微服务架构,所以各服务之间通过Spring RestClient远程调用,本来一直工作得好好的,昨天突然发现远程调用一直报错,错误详情如下: org.springframework.web.client.HttpClientErrorException$BadRequest: 400…...
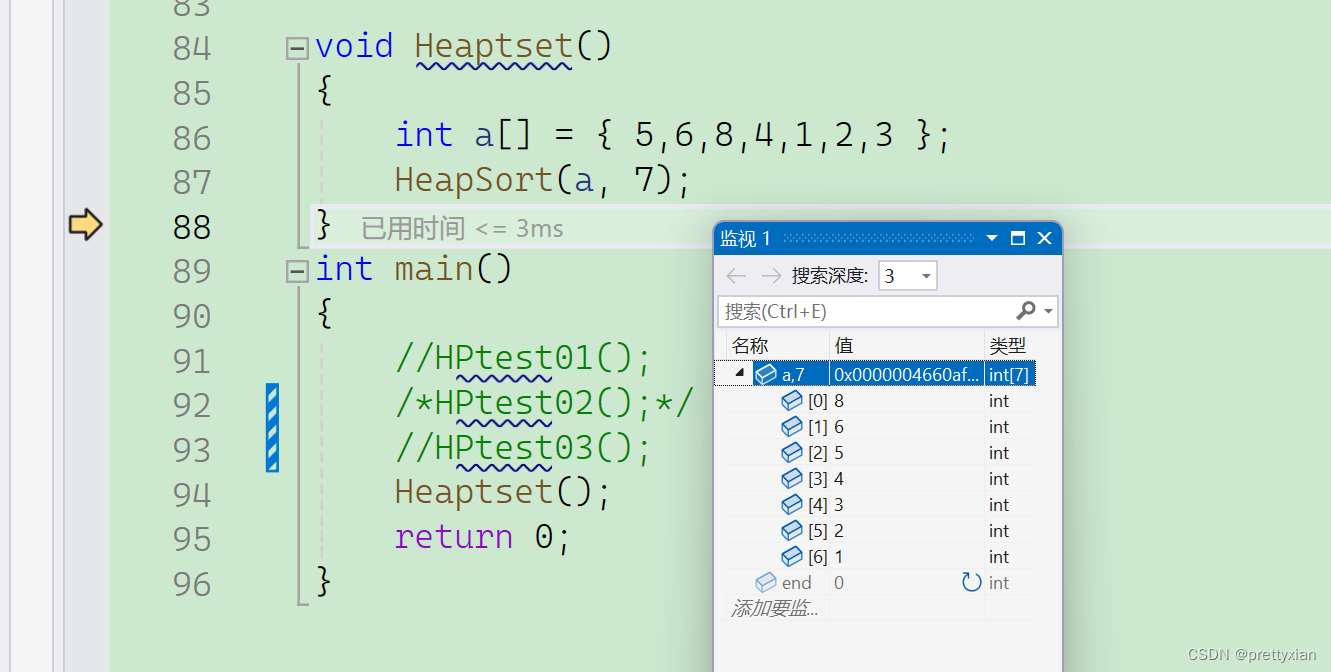
【数据结构】 -- 堆 (堆排序)(TOP-K问题)
引入 要学习堆,首先要先简单的了解一下二叉树,二叉树是一种常见的树形数据结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。它具有以下特点: 根节点(Root):树的顶部节…...

C#面:XML与 HTML 的主要区别是什么
C# XML与HTML有以下几个主要区别: 用途不同:XML(eXtensible Markup Language)是一种用于存储和传输数据的标记语言,它的主要目的是描述数据的结构和内容。HTML(HyperText Markup Language)是一…...

java并发-如何保证线程按照顺序执行?
【readme】 使用只有单个线程的线程池(最简单)Thread.join() 可重入锁 ReentrantLock Condition 条件变量(多个) ; 原理如下: 任务1执行前在锁1上阻塞;执行完成后在锁2上唤醒;任务…...

PyCharm中 Fitten Code插件的使用说明一
一. 简介 Fitten Code插件是是一款由非十大模型驱动的 AI 编程助手,它可以自动生成代码,提升开发效率,帮您调试 Bug,节省您的时间,另外还可以对话聊天,解决您编程碰到的问题。 前一篇文章学习了 PyCharm…...
Polar Web【简单】PHP反序列化初试
Polar Web【简单】PHP反序列化初试 Contents Polar Web【简单】PHP反序列化初试思路EXP手动脚本PythonGo 运行&总结 思路 启动环境,显示下图中的PHP代码,于是展开分析: 首先发现Easy类中有魔术函数 __wakeup() ,实现的是对成员…...
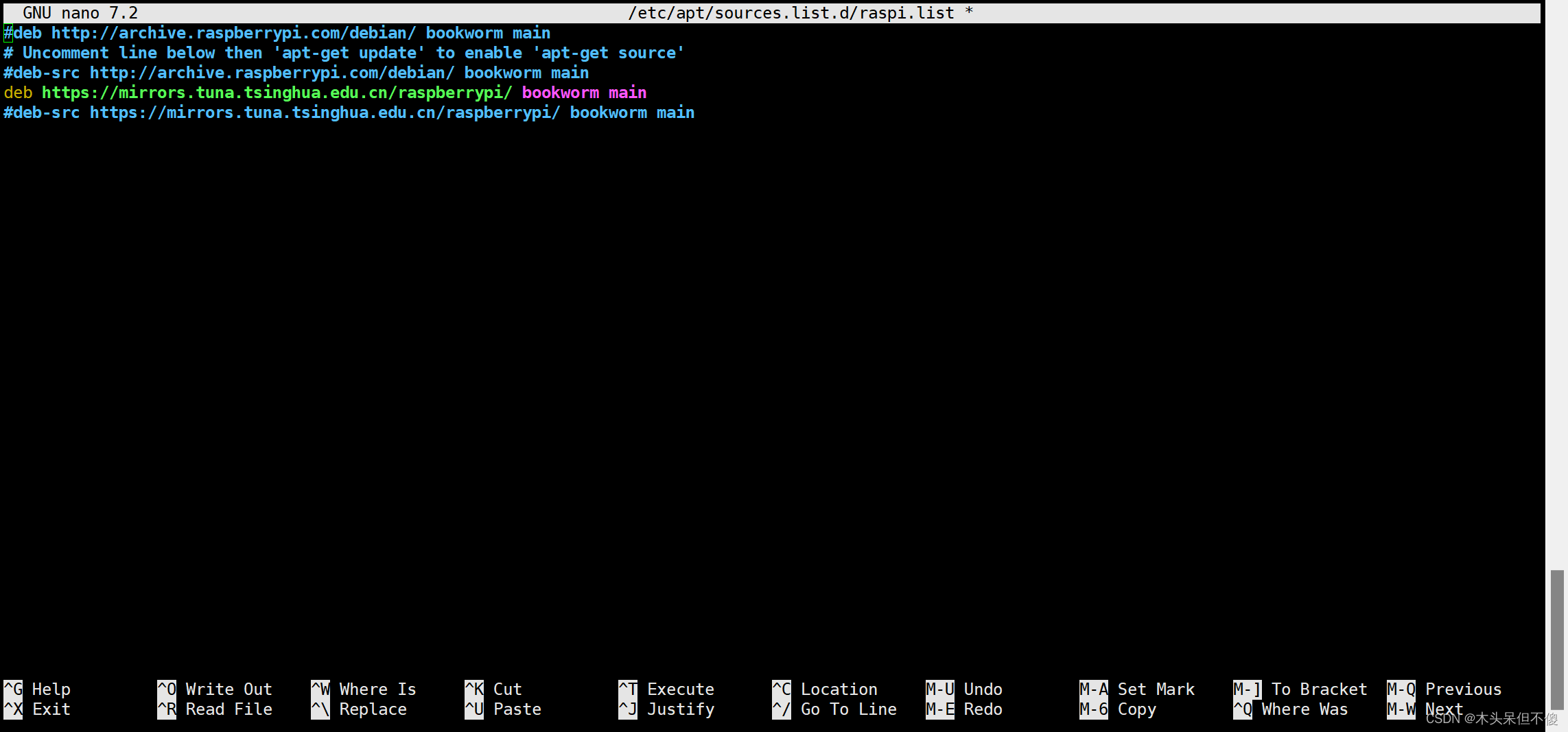
树莓派4B 零起点(二) 树莓派 更换软件源和软件仓库
目录 一、准备工作,查看自己的树莓派版本 二、安装HTTPS支持 三、更换为清华源 1、更换Debian软件源 2,更换Raspberrypi软件仓库 四、进行软件更新 接前章,我们的树莓派已经启动起来了,接下来要干的事那就是更换软件源和软件…...
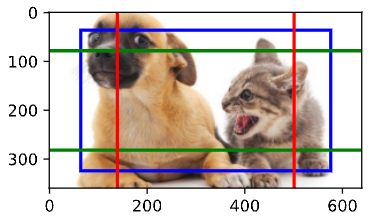
Pytorch 实现目标检测二(Pytorch 24)
一 实例操作目标检测 下面通过一个具体的例子来说明锚框标签。我们已经为加载图像中的狗和猫定义了真实边界框,其中第一个 元素是类别(0代表狗,1代表猫),其余四个元素是左上角和右下角的(x, y)轴坐标(范围…...
进行高效列表操作)
如何使用Python中的列表解析(list comprehension)进行高效列表操作
Python中的列表解析(list comprehension)是一种创建列表的简洁方法,它可以在单行代码中执行复杂的循环和条件逻辑。列表解析提供了一种快速且易于阅读的方式来生成新的列表。 以下是一些使用列表解析进行高效列表操作的示例: 1.…...

java使用websocket遇到的问题
java使用websocket的bug 1 websocket连接正常但是收不到服务端发出的消息java的websocket并发的时候导致连接断开(看着连接是正常的,但是实际上已经断开) 1 websocket连接正常但是收不到服务端发出的消息 java的websocket并发的时候导致连接断…...

[Cloud Networking] Layer 2
文章目录 1. 什么是Mac Address?2. 如何查找MAC地址?3. 二层数据交换4. [Layer 2 Protocol](https://blog.csdn.net/settingsun1225/article/details/139552315) 1. 什么是Mac Address? MAC 地址是计算机的唯一48位硬件编码,嵌入到网卡中。 MAC地址也…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...
