【背包题】oj题库
目录
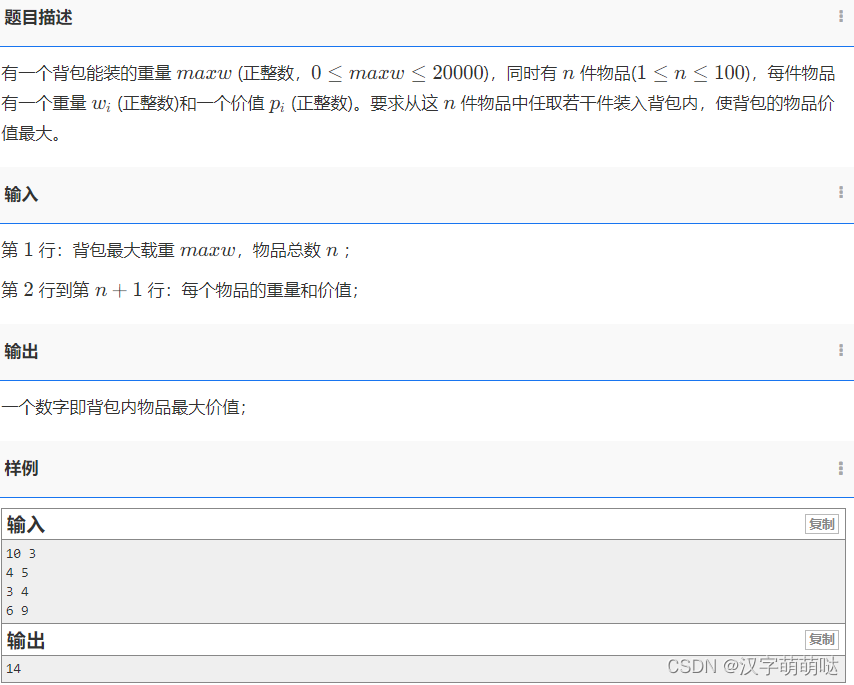
1282 - 简单背包问题
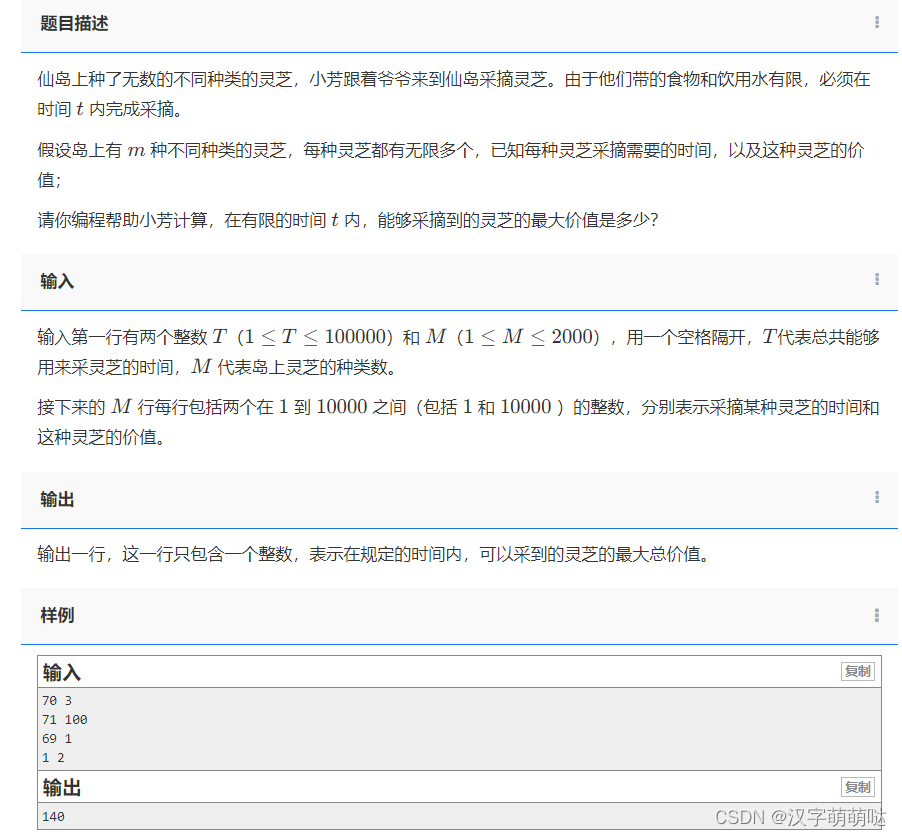
1780 - 采灵芝
1888 - 多重背包(1)编辑
1891 - 开心的金明
2073 - 码头的集装箱
1905 - 混合背包
1282 - 简单背包问题
#include <bits/stdc++.h>
using namespace std;
//二维数组:dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]])
//一维数组滚动优化:
//状态转移方程:dp[j]=max(dp[j],v[i]+dp[j-w[i]])
int w;//背包容量
int dp[20010];
int n,wi,vi;int main() {cin>>w>>n;//遍历每个物品for(int i=1; i <= n; i++) {cin>>wi>>vi;
//倒过来循环for(int j=w; j>= wi; j--) {
//讨论每个物品选和不选的两个状态
//取能到的价值的最大值dp[j]= max(dp[j],dp[j-wi]+ vi);}}cout<<dp[w];return 0;
}#include <bits/stdc++.h>
using namespace std;//动态转移方程:dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]])
//c:代表背包容量
//dp[i][j]:有i件物品,背包容量为了的情况下存储的最大价值
int c,dp[110][20100],w[110],v[110],i,j,n;
int main() {
//读入cin>>c>>n;for(i =1; i<= n; i++) {cin>>w[i]>>v[i];}//递推求 dp 数组//i:代表物品数量for(i = 1; i <= n; i++) {//在i件物品,讨论背包容量分别是1~c的情况下,最大价值//j:代表背包容量for(j= 1; j<= c; j++) {//如果能放得下if(w[i]<= j) {dp[i][j]= max(dp[i-1][j],v[i]+dp[i-1][j-w[i]]);} else {//放不下dp[i][j]= dp[i-1][j];}}}//输出n件物品,背包容量为c的最大价值cout<<dp[n][c];return 0;
}1780 - 采灵芝

#include <bits/stdc++.h>
using namespace std;/*完全背包状态转移方程
二维写法:f[i][j]= max(f[i-1]], f[i][j-w[i]]+v[])
一维写法:f[]j=max(f[j],f-w[i]]+v[i])
一维状态转义方程和01背包一致,要注意,完全背包要从前往后推导。*/
int t,m;
int f[100010];
int ti,vi;//每个物品的采摘时间和价值
int main() {cin>>t>>m;//读入m个物品 for(int i = 1; i<= m; i++) {cin>>ti>>vi;//正序循环
//从当前物品的重量(采摘时间)~背包容量最大时间)循环for(int j = ti; j <= t; j++) {f[j] = max(f[j],f[j-ti]+vi);}}cout<<f[t];//背包能够存储的最大价值return 0;
}1888 - 多重背包(1)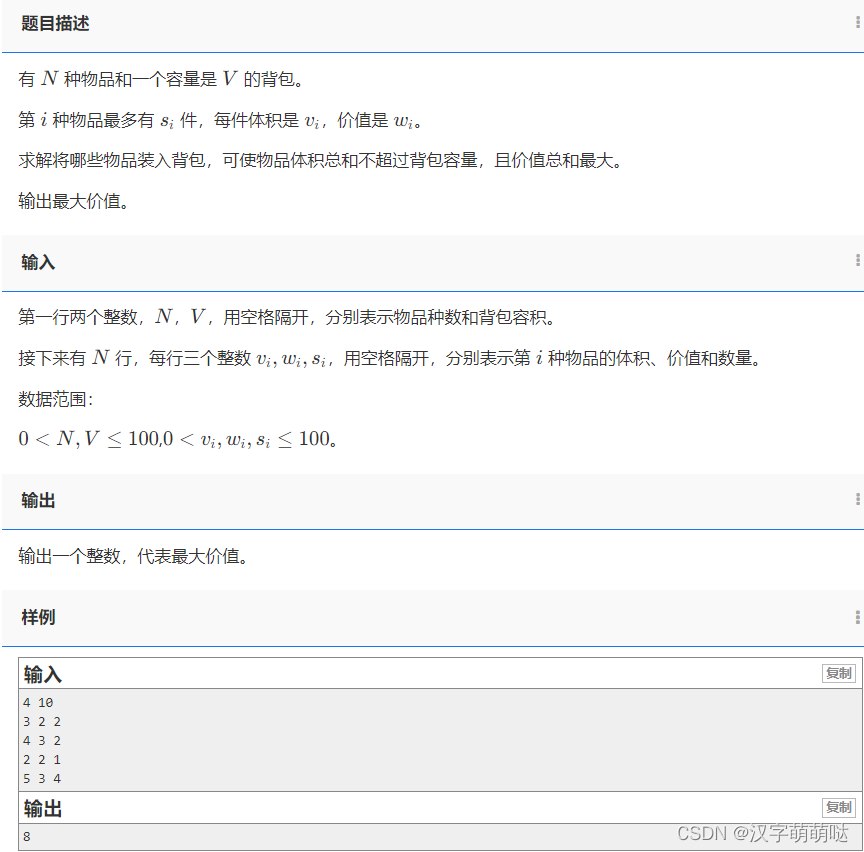
#include <bits/stdc++.h>
using namespace std;
/*01背包:每种物品有1件
完全背包:每种物品有无限件数多
重背包:每种物品有Si件
解题思路:将多重背包转换为01背包
将si件物品都存起来,转换为有si个物品,每个物品有1件*/
int n,c;//c背包容量
int v[10010],w[10010];
int dp[110];
int vi,wi,si,k;//k代表数组下标
int main() {cin>>n>>c;for(int i=1; i <= n; i++) {cin>>vi>>wi>>si;//第i个物品有si件,都存入数组for(int j=1; j<= si; j++) {k++;v[k]= vi;w[k]= wi;}}
//01 背包for(int i=1; i <= k; i++) { //逆序从背包容量循环到当前物品体积for(int j=c; j >= v[i]; j--) {dp[j]= max(dp[j],dp[j-v[i]]+w[i]);}}cout<<dp[c];return 0;
}#include <bits/stdc++.h>
using namespace std;
/*01背包:每种物品有1件
完全背包:每种物品有无限件数多
重背包:每种物品有Si件
解题思路:将多重背包转换为01背包
将si件物品都存起来,转换为有si个物品,每个物品有1件*/
int n,c;//c背包容量
int v[110],w[110],s[110];
int dp[110];int main() {cin>>n>>c;for(int i=1; i <= n; i++) {cin>>v[i]>>w[i]>>s[i];//第i个物品有si件,都存入数组}
//01 背包
//有n个物品for(int i=1; i<= n; i++) {for(int k=1; k<= s[i]; k++) {//逆序从背包容量循环到当前物品体积for(int j=c; j>= v[i]; j--) {dp[j]= max(dp[j],dp[j-v[i]]+w[i]);}}}
// for(int i=1; i <= k; i++) {
// //逆序从背包容量循环到当前物品体积
// for(int j=c; j >= v[i]; j--) {
// dp[j]= max(dp[j],dp[j-v[i]]+w[i]);
// }
// }cout<<dp[c];return 0;
}1891 - 开心的金明
题目描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过NN元钱就行”。今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的NN元。于是,他把每件物品规定了一个重要度,分为55等:用整数1-51−5表示,第55等最重要。他还从因特网上查到了每件物品的价格(都是整数元)。他希望在不超过NN元(可以等于NN元)的前提下,使每件物品的价格与重要度的乘积的总和最大。
设第jj件物品的价格为v[j]v[j],重要度为w[j]w[j],共选中了kk件物品,编号依次为j_1,j_2,…,j_kj1,j2,…,jk,则所求的总和为:
v[j_1] \times w[j_1]+v[j_2] \times w[j_2]+ …+v[j_k] \times w[j_k]v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]。
请你帮助金明设计一个满足要求的购物单。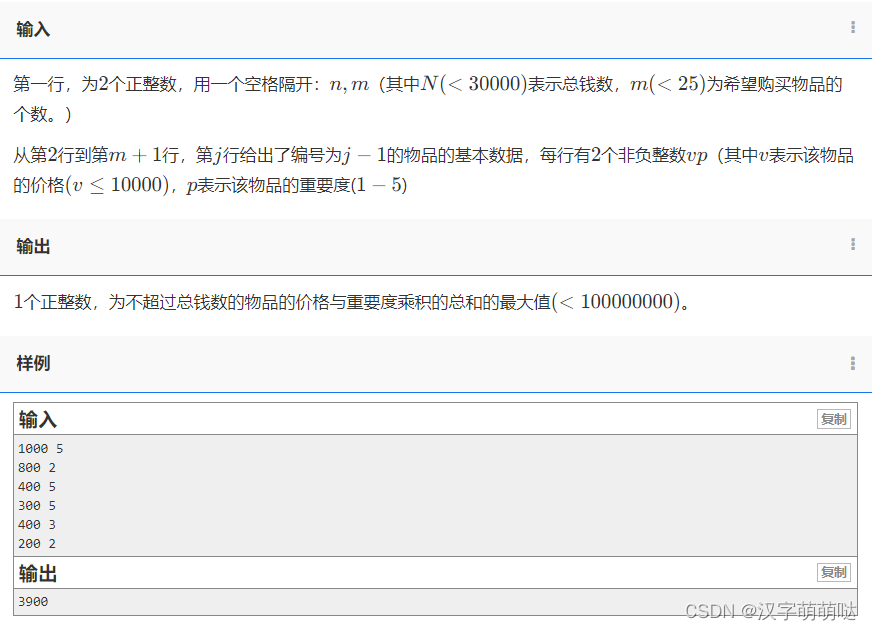
#include <bits/stdc++.h>
using namespace std;int w[30],v[30],f[50000];
//w数组为重要度,v数组为money,f是用来dp的数组
int n,m;//n是总物品个数,m是总钱数
int main() {cin>>m>>n;//输入for(int i=1; i<=n; i++) {cin>>v[i]>>w[i];w[i]*=v[i];//v数组在这里意义变为总收获(重要度*money)}
//01背包(参照第二类模板“一维数组优化”for(int i=1; i<=n; i++) {for(int j=m; j>=v[i]; j--) {
//注意从m开始if(j>=v[i]) {f[j]=max(f[j],f[j-v[i]]+w[i]);//dp}}}cout<<f[m]<<endl;//背包大小为m时最大值return 0;
}2073 - 码头的集装箱
题目描述
码头上停泊一艘远洋轮船,轮船可以装下 cc 吨的货物,码头上有 nn 个集装箱需要运走,已知第 ii 个集装箱的重量为w_iwi。
请你编程计算,在不超出轮船最大载重量的情况下,该轮船最多可以运走多少吨的集装箱。(注意:单个集装箱不能拆开运送,对于每个集装箱来说,要么整个运到轮船上,要么不运)

#include <bits/stdc++.h>
using namespace std;int n,c,w;
int f[40000];
int main() {cin>>n>>c;for(int i = 1; i <= n; i++) {cin>>w;for(int j=c; j>=w; j--) {f[j] = max(f[j],f[j-w]+w);}}cout<<f[c];
return 0;
}1905 - 混合背包
题目描述
有 NN 种物品和一个容量是 VV 的背包。
物品一共有三类:
-
第一类物品只能用 11 次(01背包);
-
第二类物品可以用无限次(完全背包);
-
第三类物品最多只能用 s_isi 次(多重背包);
每种体积是 v_ivi,价值是 w_iwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。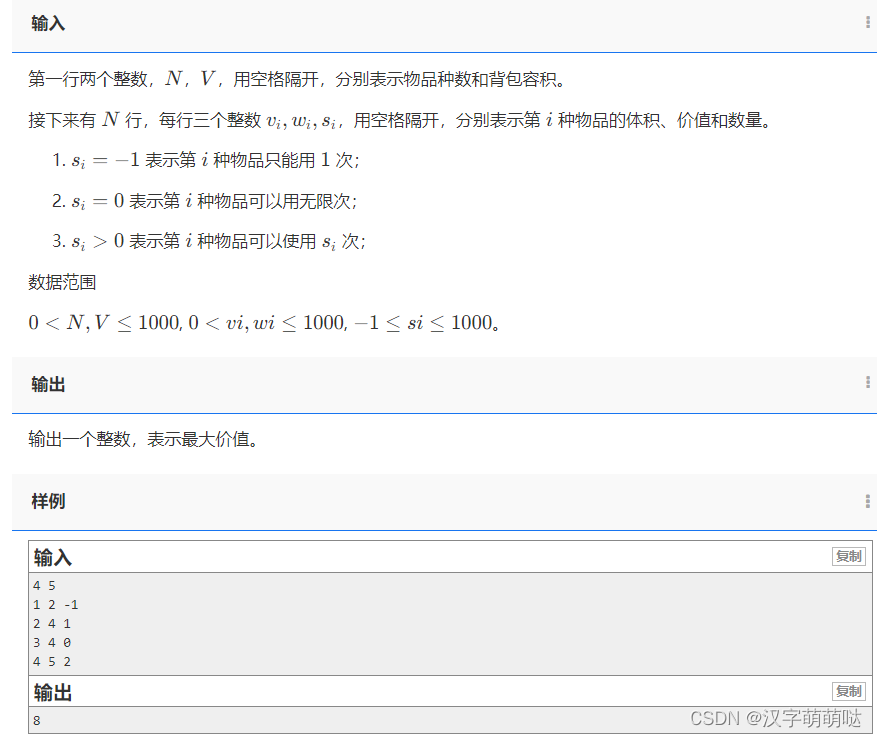
#include <bits/stdc++.h>
using namespace std;
const int N=20000;
int v[N],w[N],s[N];
int vi,wi,si;
int k=0;//表示存入数组的数据量
int dp[1010];
int n,m;
int main() {cin>>n>>m;for(int i=1; i<= n; i++) {cin>>vi>>wi>>si;//如果是多重背包,做二进制拆分if(si > 0) {int t=1;while(t<= si) {k++;w[k]= t * wi;v[k]= t * vi;s[k]=-1;//转换为 01 背包si= si -t;t= t * 2;}if(si >0) {k++;w[k]= si * wi;v[k]= si * vi;s[k]=-1;//01背包}} else {k++;w[k]= wi;v[k]= vi;s[k]= si;}}
//计算//循环k个物品for(int i=1; i<= k; i++) { //判断是01背包还是完全背包if(s[i]== -1) {for(int j= m; j >= v[i]; j--) {dp[j]= max(dp[j],dp[j-v[i]]+w[i]);}} else {for(int j = v[i]; j<= m; j++) {dp[j]= max(dp[j],dp[j-v[i]]+w[i]);}}}cout<<dp[m];return 0;
}相关文章:

【背包题】oj题库
目录 1282 - 简单背包问题 1780 - 采灵芝 1888 - 多重背包(1)编辑 1891 - 开心的金明 2073 - 码头的集装箱 1905 - 混合背包 1282 - 简单背包问题 #include <bits/stdc.h> using namespace std; //二维数组:dp[i][j]max(dp[i-1][j],v[i]dp[…...

Web前端弱势因素:深入探讨与挑战解析
Web前端弱势因素:深入探讨与挑战解析 在快速发展的Web前端领域,尽管技术日新月异,但仍存在一些固有的弱势因素。这些因素不仅影响了开发效率和用户体验,也带来了诸多挑战。本文将深入探讨Web前端的弱势因素,并从四个方…...
元素在超出当前界面的下拉列表中如何定位
有时我们会遇到一种情况是,当我们找一个视频列表中的视频,在页面的最底层,此时selenium 无法定位到这个元素,因为 selenium只能定位页面上显示出来内容的元素,需要通过下拉框把界面拉到该元素所在的位置,再…...
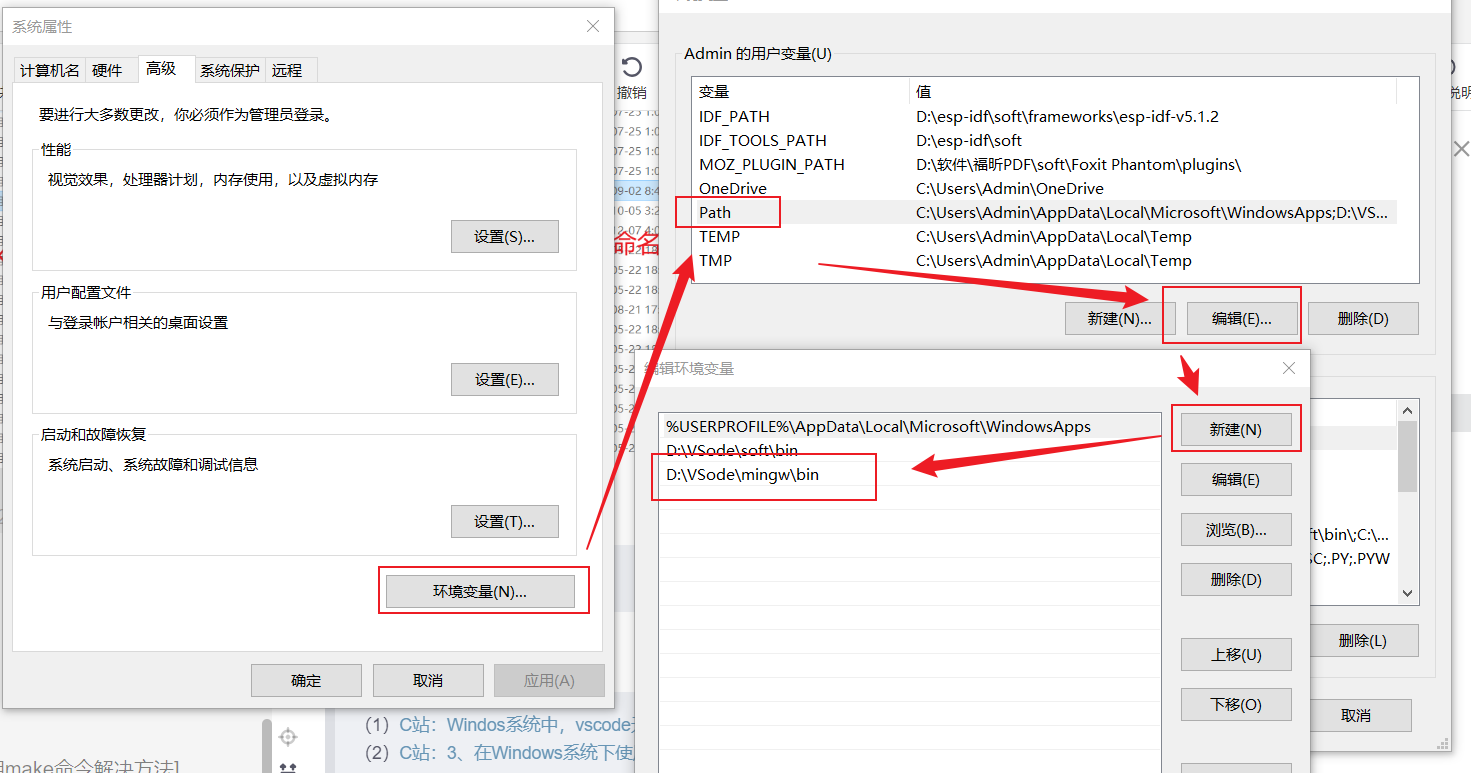
Vscode中使用make命令
前言 需要注意,如下操作需要进行网络代理,否则会出现安装失败的情况 安装 第一步 — 安装MingGW (1)进入官网下载 (2)下载完成之后,双击exe文件 (3)点击Install &#x…...
配置完eslint没有用?
当你使用 npx eslint --init 生成配置文件后 你也配置好了.prettierrc 当你在代码写一点小问题的时候 发现eslint没有进行检查 原因是你生成的 .eslintrc.js中没有加上这个配置 extends: [.....plugin:prettier/recommended],加上以后重启vscode你会发现...
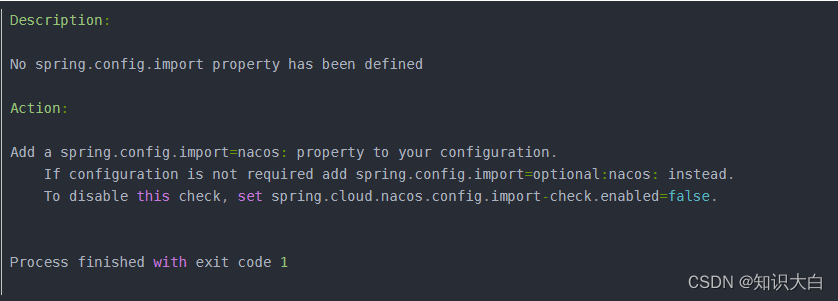
[Nacos]No spring.config.import property has been defined
在学习 Spring Cloud Alibaba ,Nacos组件,创建一个cloudalibaba-config-nacos-client,加载多配置集时遇到问题 配置了 bootstrap.yml 后启动项目报错: 是因为在springcloud 2020.0.2版本中把bootstrap的相关依赖从spring-cloud-s…...

【操作与配置】Pytorch环境搭建
安装显卡驱动 显卡驱动是一种软件程序,用于控制显卡硬件与操作系统之间的通信和交互。显卡驱动负责向操作系统提供有关显卡硬件的信息,以及使操作系统能够正确地控制和管理显卡的各种功能和性能。显卡驱动还包含了针对不同应用程序和游戏的优化ÿ…...
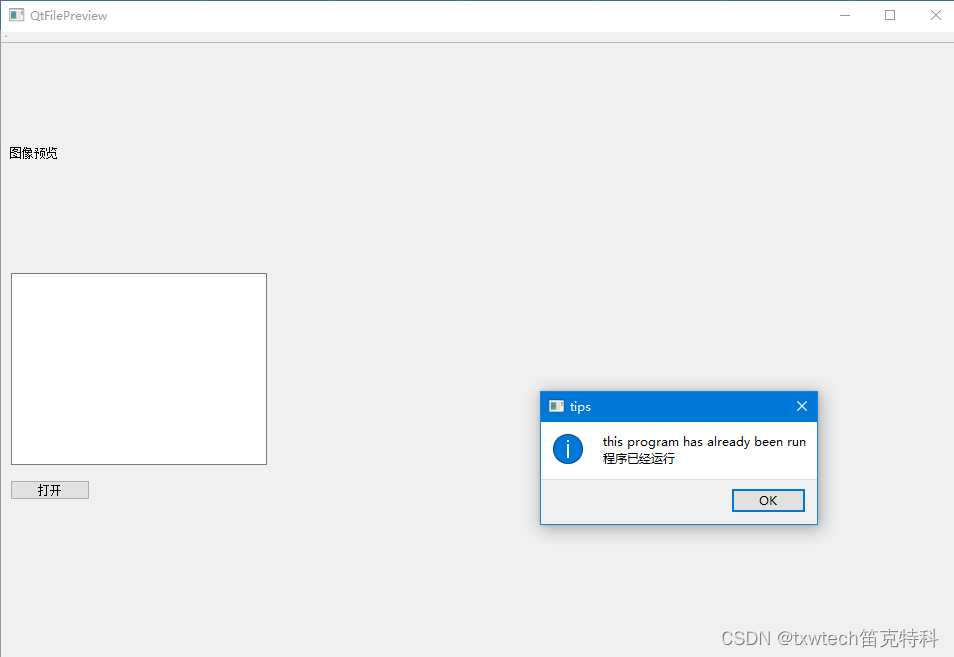
判断QT程序是否重复运行
打开exe,再次打开进行提示。 main.cpp添加: #include "QtFilePreview.h" #include <QtWidgets/QApplication> #include <windows.h> #include <qmessagebox.h> #pragma execution_character_set("utf-8")bool Ch…...

利用Axios封装及泛型实现定制化HTTP请求处理
本案例旨在教授如何使用Axios库结合TypeScript泛型进行HTTP请求的高级封装,以提升代码的可复用性和类型安全性。我们将通过一个具体的示例,学习如何创建一个通用的请求函数,它能够适应不同类型的API响应,并在请求前后加入自定义逻…...
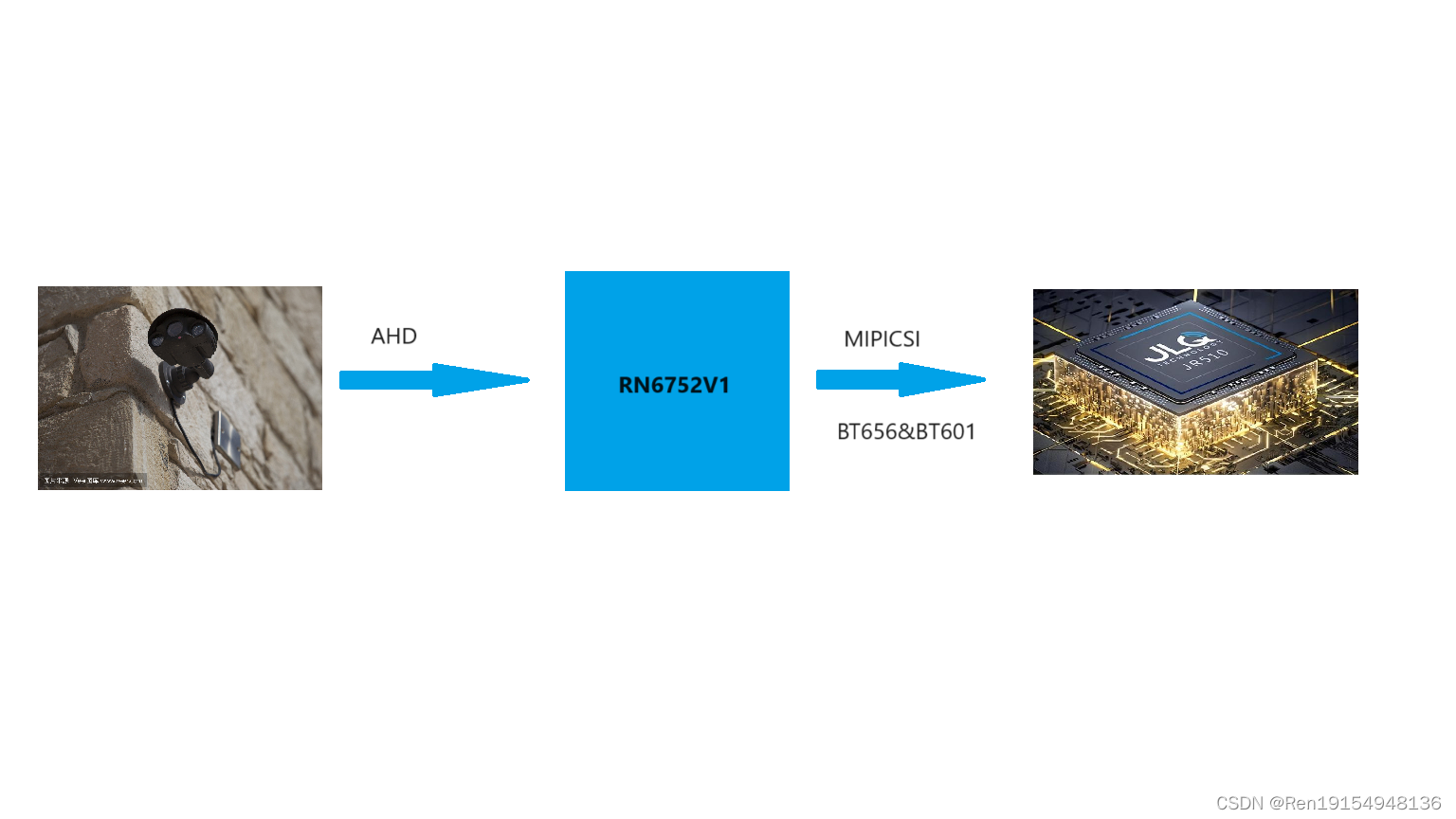
RN6752V1 高性能AHD转MIPIDVPBT656BT601芯片方案,目前适用于车载方案居多
RN6752V1描述: RN6752V1是一种模拟高清晰度(模拟高清)视频解码器IC,专为汽车应用而设计。它集成了所有必要的功能块: AFE,PLL,解码逻辑,MIPI和I2C接口等,在一个小的5mm …...

Rust 基金会的商标政策更新引发社区争议
Rust 基金会最近更新了其商标政策,引发了社区内的一些争议。 Rust 是一种高性能系统编程语言,拥有庞大的开发者社区。Rust 基金会成立于 2020 年,旨在支持和推动 Rust 语言的发展。该基金会负责管理 Rust 的商标,并制定了商标使用…...

Java Opencv识别图片上的虫子
最近有个需求,希望识别图片上的虫子,对于java来说,图像识别不是很好做。在网上也搜索了很多,很多的代码都是不完整,或者下载下载报错,有的写的很长看不懂。所以自己试着用java的opencv写了一段代码。发现识…...
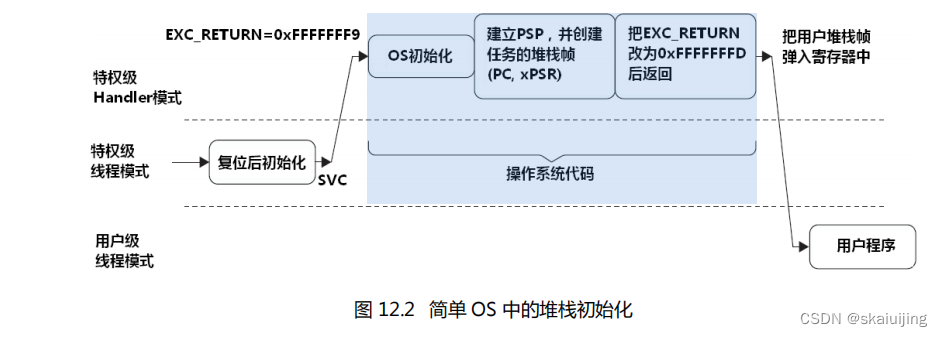
微型操作系统内核源码详解系列五(1):arm cortex m3架构
系列一:微型操作系统内核源码详解系列一:rtos内核源码概论篇(以freertos为例)-CSDN博客 系列二:微型操作系统内核源码详解系列二:数据结构和对象篇(以freertos为例)-CSDN博客 系列…...
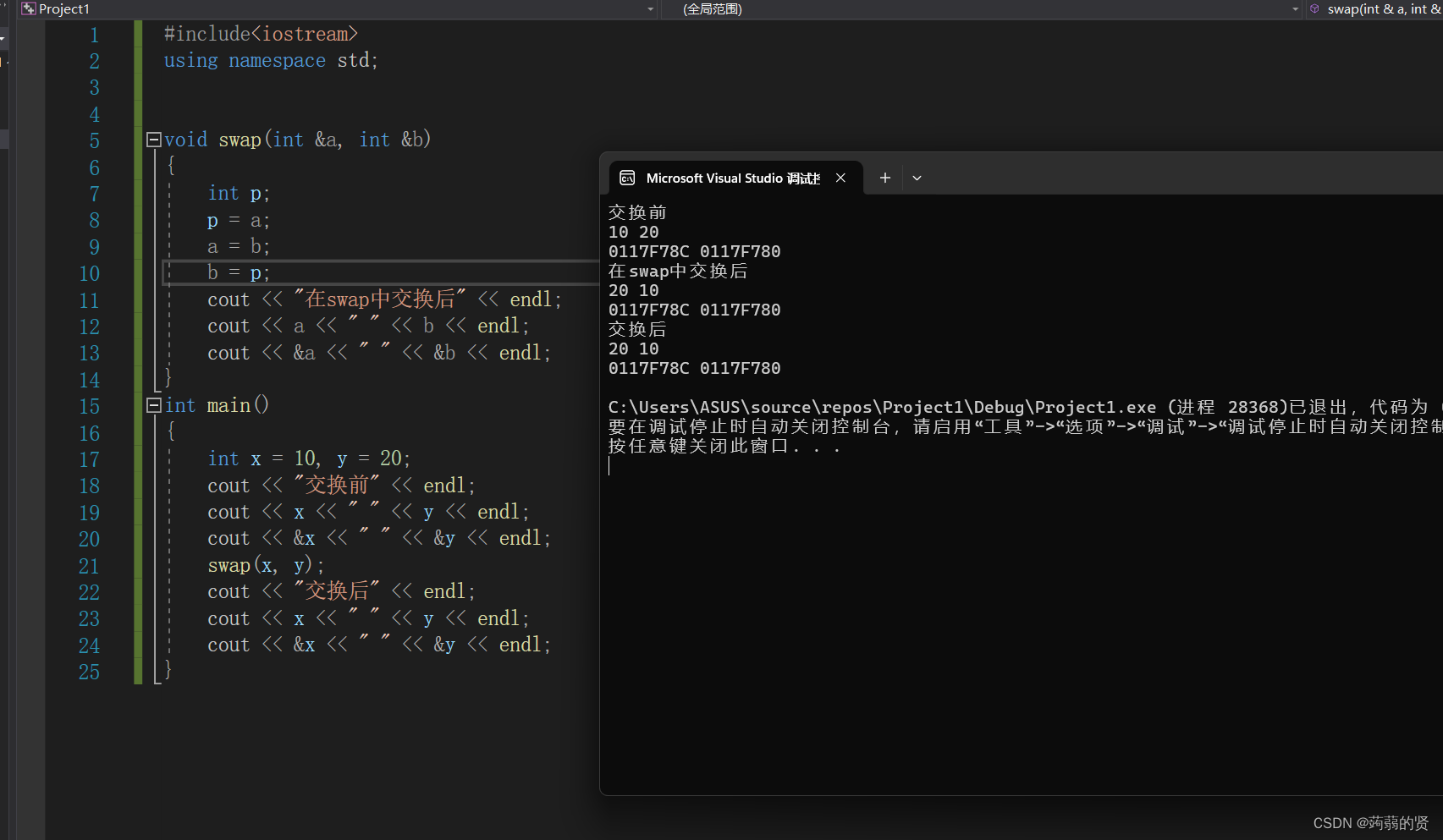
值传递和址传递
值传递 上面的代码是想要交换x,y的值,把x,y传递给swap函数之后,执行下面的操作: 在swap中a和b交换了,但是和x,y没有关系,所以x,y在main中不会变。 址传递 下面再看把x…...

【three.js】自定义物体形状BufferGeometry
目录 一、认识缓冲类型几何体BufferGeometry 二、将各个顶点连线 一、认识缓冲类型几何体BufferGeometry threejs的长方体BoxGeometry、球体SphereGeometry等几何体都是基于BoxGeometry类构建的,BufferGeometry是一个没有任何形状的空几何体,你可以通过BufferGeometry自定…...

Mac 使用 Homebrew 安装 Python3
在macOS系统中,使用Homebrew安装Python3并进行环境配置的步骤如下: 打开终端。 运行以下命令安装Python3: brew install python3 安装完成后,可以通过以下命令检查Python3的版本: python3 --version 为了确保终端…...
汽车行驶中是怎么保障轴瓦安全的?
汽车轴瓦是一种用于减少摩擦和支撑转动部件的关键零部件,通常用于发动机的曲轴、凸轮轴等转动部件上。主要作用是减少转动部件之间的摩擦,支撑和保护曲轴、凸轮轴等旋转部件,确保它们在高速旋转时的稳定性和耐用性。 在汽车轴瓦加工过程中&am…...

洗地机哪款好?洗地机十大名牌排行榜
随着科技的发展,各种家居清洁工具层出不穷,为我们的生活带来了诸多便利。在众多清洁工具中,洗地机的清洁效果更受大家喜爱,它能够完美解决了扫地机无法做到的干湿垃圾“一遍清洁”效果,而且几乎能解决日常生活中所有的…...
)
spark mllib 特征学习笔记 (二)
当然,请继续介绍其他特征处理方法的公式、适用场景和案例: 10. StringIndexer 公式: 将字符串类型的标签转换为数值索引: StringIndexer ( x ) { 0 , 1 , 2 , … , N − 1 } \text{StringIndexer}(x) \{0, 1, 2, \ldots, N-1…...

湘潭大学软件工程数据库2(题型,复习资源和计划)
文章目录 选择题关系范式事务分析E-R 图sql作业题答案链接(仅限有官方答案的版本)结语 现在实验全部做完了,实验和作业占比是百分之 40 ,通过上图可以看出来,重点是 sql 语言 所以接下来主要就是学习 sql 语句怎么书写…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
