激光点云配准算法——Cofinet / GeoTransforme / MAC
激光点云配准算法——Cofinet / GeoTransformer / MAC
GeoTransformer + MAC是当前最SOTA的点云匹配算法,在之前我用总结过视觉特征匹配的相关算法
视觉SLAM总结——SuperPoint / SuperGlue
本篇博客对Cofinet、GeoTransformer、MAC三篇论文进行简单总结
1. Cofinet
Cofinet发表于2021年ICCV,原文为《CoFiNet: Reliable Coarse-to-fine Correspondences
for Robust Point Cloud Registration》,对这篇文章进行总结是因为它可以算作GeoTransformer的前身,其首次提出Coarse-To-Fine的点云匹配框架
Cofinet算法框架如下图所示:

算法主要又两部分组成,Correspondence Proposal Block和Correspondence Refinement Block
1.1 Correspondence Proposal Block
Point Encoding:对于输入的点云 P X ∈ R n × 3 , P Y ∈ R m × 3 P_X \in R^{n \times 3}, P_Y \in R^{m \times 3} PX∈Rn×3,PY∈Rm×3,使用KPConv进行特征提取,KPConv的细节在下文介绍,输出经过下采样的SuperPoint P X ′ ∈ R n ′ × 3 , P Y ′ ∈ R r n ′ × 3 P_X^{\prime} \in R^{n^{\prime} \times 3}, P_Y^{\prime} \in R^{r n^{\prime} \times 3} PX′∈Rn′×3,PY′∈Rrn′×3及其特征 F X ′ ∈ R n ′ × b , F Y ′ ∈ R m ′ × b F_X^{\prime} \in R^{n^{\prime} \times b}, F_Y^{\prime} \in R^{m^{\prime} \times b} FX′∈Rn′×b,FY′∈Rm′×b, 其中 b = 256 b=256 b=256: P X → P ′ X , F ′ X P Y → P ′ Y , F ′ Y \begin{aligned} & P_X \rightarrow P^{\prime}{ }_X, F^{\prime}{ }_X \\ & P_Y \rightarrow P^{\prime}{ }_Y, F^{\prime}{ }_Y \end{aligned} PX→P′X,F′XPY→P′Y,F′Y每个经过下采样得到SuperPoint表征了原输入点云一个小Patch上的所有信息
Attentional Feature Aggregation:对于SuperPoint P X ′ ∈ R n ′ × 3 , P Y ′ ∈ R r n ′ × 3 P_X^{\prime} \in R^{n^{\prime} \times 3}, P_Y^{\prime} \in R^{r n^{\prime} \times 3} PX′∈Rn′×3,PY′∈Rrn′×3及其特征 F X ′ ∈ R n ′ × b , F Y ′ ∈ R m ′ × b F_X^{\prime} \in R^{n^{\prime} \times b}, F_Y^{\prime} \in R^{m^{\prime} \times b} FX′∈Rn′×b,FY′∈Rm′×b进行Self-Attention和Cross-Attention操作,Self-Attention用于扩大感受野,Cross-Attention用于信息交互: F ′ X → F ~ ′ X F ′ Y → F ~ ′ Y \begin{aligned} & F^{\prime}{ }_X \rightarrow \tilde{F}^{\prime}{ }_X \\ & F^{\prime}{ }_Y \rightarrow \tilde{F}^{\prime}{ }_Y \end{aligned} F′X→F~′XF′Y→F~′Y
Correspondence Proposal:将 F ~ X ′ , F ~ Y ′ \tilde{F}_X^{\prime}, \tilde{F}_Y^{\prime} F~X′,F~Y′使用Sinkhorn算法构建Confidence Matrix,在训练阶段选用128对真值匹配点构建GT Confidence Matrix对Sinkhorn算法输出的Confidence Matrix进行监督,数目是固定的。在测试阶段Confidence大于0.2的匹配作为Coarse-Level的匹配结果,如果数目小于200则将阈值调整到0.01,输出的数目是不固定的。最终输出SuperPoint的Correspondence集合 C ′ = { ( P ′ X ( i ′ ) , P Y ′ ( j ′ ) ) } . C^{\prime}=\left\{\left(P^{\prime}{ }_X\left(i^{\prime}\right), P_Y^{\prime}\left(j^{\prime}\right)\right)\right\} . C′={(P′X(i′),PY′(j′))}.
其中Attention部分和Optimal Transport部分和SuperGlue中采用的算法基本一致,在此不再赘述,感兴趣的同学可以参考视觉SLAM总结——SuperPoint / SuperGlue
1.2 Correspondence Refinement Block
Node Decoding:Decoder部分使用 F ~ X ′ , F ~ Y ′ \tilde{F}_X^{\prime}, \tilde{F}_Y^{\prime} F~X′,F~Y′作为输入,同样使用KPConv进行维度恢复,最终输出Point Level的特征 F X ∈ R n × c , F Y ∈ R m × c F_X \in R^{n \times c}, F_Y \in R^{m \times c} FX∈Rn×c,FY∈Rm×c,其中 c = 32 c=32 c=32
Point-To-Node Grouping:这部分的目的是将SuperPoint的Correspondence扩展为Point Level Correspondence,基于Point Level Correspondence再进一步求解位姿。这里使用的KNN建立SuperPoint和Point的关联,经过这个步骤后,每个SuperPoint P X ′ ( i ′ ) P_X^{\prime}\left(i^{\prime}\right) PX′(i′)会被分配一定数量的Point,这些Point构成了一个Patch G i ′ G_{i^{\prime}} Gi′,每个Patch的点的数量如果超过64个就会进行截断。 G i ′ P = { p ∈ P X ∣ ∥ p − P ′ X ( i ′ ) ∥ ≤ ∥ p − P ′ X ( j ′ ) ∥ , ∀ j ′ ≠ i ′ } G_{i^{\prime}}^P=\left\{p \in P_X \mid\left\|p-P^{\prime}{ }_X\left(i^{\prime}\right)\right\| \leq\left\|p-P^{\prime}{ }_X\left(j^{\prime}\right)\right\|, \forall j^{\prime} \neq i^{\prime}\right\} Gi′P={p∈PX∣∥p−P′X(i′)∥≤∥p−P′X(j′)∥,∀j′=i′} G i ′ F = { f ∈ F X ∣ f ↔ pwithp ∈ G i ′ P } G_{i^{\prime}}^F=\left\{f \in F_X \mid f \leftrightarrow \text { pwithp } \in G_{i^{\prime}}^P\right\} Gi′F={f∈FX∣f↔ pwithp ∈Gi′P}通过上述操作之后Patch和Patch之间在欧式空间和特征空间会分别构成集合: C P = { ( G i ′ P , G j ′ P ) } C_P=\left\{\left(G_{i^{\prime}}^P, G_{j^{\prime}}^P\right)\right\} CP={(Gi′P,Gj′P)} C F = { ( G i ′ F , G j ′ F ) } C_F=\left\{\left(G_{i^{\prime}}^F, G_{j^{\prime}}^F\right)\right\} CF={(Gi′F,Gj′F)}
Density-Adaptive Matching:接着对每一个Patch进行Point Level的Correspondence提取,Point Level级别无法直接使用Sinkhorn算法,原因是每个Patch中的存在的点的数量是不一致的,当两个点数不一致的Patch构建Similarity Matrix时点数不足的位置使用 − ∞ -\infty −∞进行填充,然后再使用Sinkhorn算法就可以消除点数不一致给模型带来的影响。
在获得Point Level的Correspondence后,仍然使用RANSAC方法进行旋转平移求解。
1.3 Loss
Coarse Scale损失函数如下: L c = − ∑ i ′ , j ′ W ′ ( i ′ , j ′ ) log ( S ′ ( i ′ , j ′ ) ) ∑ i ′ , j ′ W ′ ( i ′ , j ′ ) . \mathcal{L}_c=\frac{-\sum_{i^{\prime}, j^{\prime}} \mathbf{W}^{\prime}\left(i^{\prime}, j^{\prime}\right) \log \left(\mathbf{S}^{\prime}\left(i^{\prime}, j^{\prime}\right)\right)}{\sum_{i^{\prime}, j^{\prime}} \mathbf{W}^{\prime}\left(i^{\prime}, j^{\prime}\right)} . Lc=∑i′,j′W′(i′,j′)−∑i′,j′W′(i′,j′)log(S′(i′,j′)).其中 log ( S ′ ( i ′ , j ′ ) ) \log \left(\mathbf{S}^{\prime}\left(i^{\prime}, j^{\prime}\right)\right) log(S′(i′,j′))为Sinkhorn生成的Confidence Matrix和Ground Truth的Confidence Matrix的交叉熵损失, W ′ ( i ′ , j ′ ) \mathbf{W}^{\prime}\left(i^{\prime}, j^{\prime}\right) W′(i′,j′)为加权系数,定义如下: W ′ ( i ′ , j ′ ) = { min ( r ( i ′ , j ′ ) , r ( j ′ , i ′ ) ) , i ′ ≤ n ′ ∧ j ′ ≤ m ′ , 1 − r ( i ′ ) , i ′ ≤ n ′ ∧ j ′ = m ′ + 1 , 1 − r ( j ′ ) , i ′ = n ′ + 1 ∧ j ′ ≤ m ′ , 0 , otherwise. \mathbf{W}^{\prime}\left(i^{\prime}, j^{\prime}\right)= \begin{cases}\min \left(r\left(i^{\prime}, j^{\prime}\right), r\left(j^{\prime}, i^{\prime}\right)\right), & i^{\prime} \leq n^{\prime} \wedge j^{\prime} \leq m^{\prime}, \\ 1-r\left(i^{\prime}\right), & i^{\prime} \leq n^{\prime} \wedge j^{\prime}=m^{\prime}+1, \\ 1-r\left(j^{\prime}\right), & i^{\prime}=n^{\prime}+1 \wedge j^{\prime} \leq m^{\prime}, \\ 0, & \text { otherwise. }\end{cases} W′(i′,j′)=⎩ ⎨ ⎧min(r(i′,j′),r(j′,i′)),1−r(i′),1−r(j′),0,i′≤n′∧j′≤m′,i′≤n′∧j′=m′+1,i′=n′+1∧j′≤m′, otherwise. 其中 r ( i ′ ) r\left(i^{\prime}\right) r(i′)为单个Patch中Overlap点所占比例,定义如下: r ( i ′ ) = ∣ { p ∈ G i ′ P ∣ ∃ q ∈ P Y s.t. ∥ T ‾ Y X ( p ) − q ∥ < τ p } ∣ ∣ G i ′ P ∣ , r\left(i^{\prime}\right)=\frac{\mid\left\{\mathbf{p} \in \mathbf{G}_{i^{\prime}}^{\mathbf{P}} \mid \exists \mathbf{q} \in \mathbf{P}_{\mathbf{Y}} \text { s.t. }\left\|\overline{\mathbf{T}}_{\mathbf{Y}}^{\mathbf{X}}(\mathbf{p})-\mathbf{q}\right\|<\tau_p\right\} \mid}{\left|\mathbf{G}_{i^{\prime}}^{\mathbf{P}}\right|}, r(i′)= Gi′P ∣{p∈Gi′P∣∃q∈PY s.t. TYX(p)−q <τp}∣, r ( i ′ , j ′ ) r\left(i^{\prime}, j^{\prime}\right) r(i′,j′)为两个Patch相互Overlap点所占比例,定义如下: r ( i ′ , j ′ ) = ∣ { p ∈ G i ′ P ∣ ∃ q ∈ G j ′ P s.t. ∥ T ‾ Y X ( p ) − q ∥ < τ p } ∣ ∣ G i ′ P ∣ r\left(i^{\prime}, j^{\prime}\right)=\frac{\mid\left\{\mathbf{p} \in \mathbf{G}_{i^{\prime}}^{\mathbf{P}} \mid \exists \mathbf{q} \in \mathbf{G}_{j^{\prime}}^{\mathbf{P}} \text { s.t. }\left\|\overline{\mathbf{T}}_{\mathbf{Y}}^{\mathbf{X}}(\mathbf{p})-\mathbf{q}\right\|<\tau_p\right\} \mid}{\left|\mathbf{G}_{i^{\prime}}^{\mathbf{P}}\right|} r(i′,j′)= Gi′P ∣{p∈Gi′P∣∃q∈Gj′P s.t. TYX(p)−q <τp}∣这里其实很好理解,当Patch中被覆盖的点的占比越高,说明这个Patch被匹配的可能性越大,权重也就应该越高。
Finer Scale的损失函数如下: L f = − ∑ l , i , j B ~ ( l ) ( i , j ) log ( S ~ ( l ) ( i , j ) ) ∑ l , i , j B ~ ( l ) ( i , j ) \mathcal{L}_f=\frac{-\sum_{l, i, j} \widetilde{\mathbf{B}}^{(l)}(i, j) \log \left(\widetilde{\mathbf{S}}^{(l)}(i, j)\right)}{\sum_{l, i, j} \widetilde{\mathbf{B}}^{(l)}(i, j)} Lf=∑l,i,jB (l)(i,j)−∑l,i,jB (l)(i,j)log(S (l)(i,j))其中交叉熵函数的定义是相同的,对于加权系数的定义如下: B ~ ( l ) ( i , j ) = { 1 , ∥ T ~ Y X ( G ~ i ′ P ( i ) ) − G ~ j ′ P ( j ) ∥ < τ p , 0 , otherwise , ∀ i , ∀ j ∈ [ 1 , k ] \widetilde{\mathbf{B}}^{(l)}(i, j)=\left\{\begin{array}{ll} 1, & \left\|\widetilde{\mathbf{T}}_{\mathbf{Y}}^{\mathbf{X}}\left(\widetilde{\mathbf{G}}_{i^{\prime}}^{\mathbf{P}}(i)\right)-\widetilde{\mathbf{G}}_{j^{\prime}}^{\mathbf{P}}(j)\right\|<\tau_p, \\ 0, & \text { otherwise }, \end{array} \quad \forall i, \forall j \in[1, k]\right. B (l)(i,j)={1,0, T YX(G i′P(i))−G j′P(j) <τp, otherwise ,∀i,∀j∈[1,k] B ~ ( l ) ( i , k + 1 ) = max ( 0 , 1 − ∑ j = 1 k B ~ ( l ) ( i , j ) ) , ∀ i ∈ [ 1 , k ] \widetilde{\mathbf{B}}^{(l)}(i, k+1)=\max \left(0,1-\sum_{j=1}^k \widetilde{\mathbf{B}}^{(l)}(i, j)\right), \quad \forall i \in[1, k] B (l)(i,k+1)=max(0,1−j=1∑kB (l)(i,j)),∀i∈[1,k] B ~ ( l ) ( k + 1 , j ) = max ( 0 , 1 − ∑ i = 1 k B ~ ( l ) ( i , j ) ) , ∀ j ∈ [ 1 , k ] \widetilde{\mathbf{B}}^{(l)}(k+1, j)=\max \left(0,1-\sum_{i=1}^k \widetilde{\mathbf{B}}^{(l)}(i, j)\right), \quad \forall j \in[1, k] B (l)(k+1,j)=max(0,1−i=1∑kB (l)(i,j)),∀j∈[1,k]
最终的损失函数定义为: L = L c + λ L f L=L_c+\lambda L_f L=Lc+λLf
1.4 KPConv
KPConv是PointNet作者2019年提出来的一篇文章KPConv: Flexible and Deformable Convolution for Point Clouds》,因为CofiNet恶化GeoTransformer中都有用到这个模块,因此在此对其进行一个简单总结
KPConv全称为Kernel Point Convolution,是将Kernel Point当成每个点云特征的参照物,去计算这些与这些Kernel Point的权重来更新每个点云特征。首先定义点云上某个点 x i ∈ P ∈ R N × 3 x_i \in P \in R^{N \times 3} xi∈P∈RN×3和对应的特征 f i ∈ F ∈ R N × D f_i \in F \in R^{N \times D} fi∈F∈RN×D,然后定义点云特征的卷积可以写成如下形式: ( F ∗ g ) ( x ) = ∑ x i ∈ N x g ( x i − x ) f i (F * g)(x)=\sum_{x_i \in N_x} g\left(x_i-x\right) f_i (F∗g)(x)=xi∈Nx∑g(xi−x)fi其中 g g g为卷积核函数, N x N_x Nx代表某个局部邻域 N x = { x i ∈ P ∥ ∣ x i − x ∥ ≤ r } N_x=\left\{x_i \in P\left\|\mid x_i-x\right\| \leq r\right\} Nx={xi∈P∥∣xi−x∥≤r},通常我们会对点云进行去中心化,将每一个点 x i x_i xi通过去中心化 y i = x i − x y_i=x_i-x yi=xi−x转变成 y i y_i yi,因此局部邻域 B r 3 = { y ∈ R 3 ∥ ∥ y ∥ ≤ r } B_r^3=\left\{y \in R^3\|\| y \| \leq r\right\} Br3={y∈R3∥∥y∥≤r},这样使得局部邻域中的计算具备平移不变形。
在KPConv中,作者定义了一组Kernel Points { x k ^ ∣ k < K } ∈ B r 3 \left\{\hat{x_k} \mid k<K\right\} \in B_r^3 {xk^∣k<K}∈Br3和对应的权重 { W k ∣ k < K } ∈ R D in × D out \left\{W_k \mid k<K\right\} \in R^{D_{\text {in }} \times D_{\text {out }}} {Wk∣k<K}∈RDin ×Dout ,将每个点周围的Kernel Points作为其参照物,去进行特征的聚合,基于Kernel Points的卷积核函数如下: g ( y i ) = ∑ k < K h ( y i , x k ^ ) W k g\left(y_i\right)=\sum_{k<K} h\left(y_i, \hat{x_k}\right) W_k g(yi)=k<K∑h(yi,xk^)Wk其中权重系数 h ( y i , x k ^ ) h\left(y_i, \hat{x_k}\right) h(yi,xk^)为: h ( y i , x k ^ ) = max ( 0 , 1 ∥ y i − x k ^ ∥ σ ) h\left(y_i, \hat{x_k}\right)=\max \left(0,1 \frac{\left\|y_i-\hat{x_k}\right\|}{\sigma}\right) h(yi,xk^)=max(0,1σ∥yi−xk^∥)即点和Kernel Points越接近时权重系数越大。该操作的示意图如下:

对比图像的卷积操作如下:

其区别主要在于,在图像的卷积操作中,因为像素位置和卷积核的位置都是离散的,可以很容易地找到一一对应关系,而在点云的卷积操作中,点云点位置和卷积核的位置可以看做是连续的,无法完美地找到一一对应关系,因此基于权重系数 h ( y i , x k ^ ) h\left(y_i, \hat{x_k}\right) h(yi,xk^)的求和来表达这种关系。
2. GeoTransformer
GeoTransformer发表于2022年,在这之前的大部分工作
- 采用的是先检测两个点云中的Super Point再对Super Point进行匹配的方式,如上CoFiNet所示,当两个点云重叠度很低时,找到两个可匹配的Super Point是困难的,这使得后续的其他操作的精度难以得到保证。
- Super Point描述的是点云的全局信息,为了更好地提取全局信息很多方法会使用Transformer进行点云全局特征的学习,但是Transformer会天然地忽略点云的几何信息,尽管可以使用点云坐标作为位置编码,但是基于点云坐标的位置编码都是Transformation-Invariant,也不是很不合理
针对这两点,GeoTransformer通过Super Point中Pair-Wise的距离信息和Triplet-Wise的角度信息进行编码并嵌入到Transformer中,这种显示地几何信息编码使得在低重叠度的点云匹配中具备较高的鲁棒性。也正是因为匹配的鲁棒性可以使得GeoTransformer的后处理不依赖RANSC进而使得整个算法变得很快。
GeoTransformer网络结构如下图所示:

算法整体分为4个部分,首先使用使用KPConv的Backbone进行Super Point提取,然后使用Transformer对Super Point进行匹配,进而将Super Point扩展为Patch再Patch上进行Point级别的匹配,最后使用Local-to-Global的配准方式获得最后的Transformation。
2.1 Superpoint Sampling and Feature Extraction
GeoTransformer同样使用KP Conv进行Super Point及其特征的提取,KP Conv的第一层输出为用于稠密点云匹配的Point及其特征,每个Point会根据距离将分配给各个Super Point构成Patch G i P = { p ~ ∈ P ~ ∣ i = argmin j ( ∥ p ~ − p ^ j ∥ 2 ) , p ^ j ∈ P ^ } \mathcal{G}_i^{\mathcal{P}}=\left\{\tilde{\mathbf{p}} \in \tilde{\mathcal{P}} \mid i=\operatorname{argmin}_j\left(\left\|\tilde{\mathbf{p}}-\hat{\mathbf{p}}_j\right\|_2\right), \hat{\mathbf{p}}_j \in \hat{\mathcal{P}}\right\} GiP={p~∈P~∣i=argminj(∥p~−p^j∥2),p^j∈P^}其中 P ^ \hat{\mathcal{P}} P^ 和 Q ^ \hat{\mathcal{Q}} Q^为Super Point点云, P ~ \tilde{\mathcal{P}} P~ 和 Q ~ \tilde{\mathcal{Q}} Q~稠密帧点云.
2.2 Superpoint Matching Module
GeoTransformer同样使用Self-Attention和Cross-Attention对Super Point的特征进行学习,但是与CoFiNet不同的是,GeoTransformer将几何结构显示地编码到Super Point的特征中
Geometric Self-Attention:对于Super Point点云· P ^ \hat{\mathcal{P}} P^ 和 Q ^ \hat{\mathcal{Q}} Q^我们执行如下相同的操作,定义Geometric Self-Attention输入的特征矩阵为 X ∈ R ∣ P ^ ∣ × d i \mathbf{X} \in \mathbb{R}^{|\hat{\mathcal{P}}| \times d_i} X∈R∣P^∣×di,输出的特征矩阵为 Z ∈ R ∣ P ^ ∣ × d t \mathbf{Z} \in \mathbb{R}^{|\hat{\mathcal{P}}| \times d_t} Z∈R∣P^∣×dt,Self Attention中的权重系数 e i , j e_{i, j} ei,j的计算公式如下 e i , j = ( x i W Q ) ( x j w K + r i , j w R ) T t t . e_{i, j}=\frac{\left(\mathbf{x}_i \mathbf{W}^Q\right)\left(\mathbf{x}_j \mathbf{w}^K+\mathbf{r}_{i, j} \mathbf{w}^R\right)^T}{\sqrt{t_t}} . ei,j=tt(xiWQ)(xjwK+ri,jwR)T.其中 r i , j ∈ R d t \mathbf{r}_{i, j} \in \mathbb{R}^{d_t} ri,j∈Rdt为Geometric Structure Embedding, W Q , W K , W V , W R ∈ R d t × d t \mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V, \mathbf{W}^R \in \mathbb{R}^{d_t \times d_t} WQ,WK,WV,WR∈Rdt×dt为权重矩阵,下面我们来看看Geometric Structure Embedding是如何定义的
Geometric Structure Embedding包括Pair-Wise Distance Embedding和Triplet-Wise Embedding两个部分,给定两个Super Point p ^ i , p ^ j ∈ P ^ \hat{\mathbf{p}}_i, \hat{\mathbf{p}}_j \in \hat{\mathcal{P}} p^i,p^j∈P^
Pair-Wise Distance Embedding定义为 { r i , j , 2 k D = sin ( d i , j / σ d 1000 0 2 k / d t ) r i , j , 2 k + 1 D = cos ( d i , j / σ d 1000 0 2 k / d t ) \left\{\begin{array}{c} r_{i, j, 2 k}^D=\sin \left(\frac{d_{i, j} / \sigma_d}{10000^{2 k / d_t}}\right) \\ r_{i, j, 2 k+1}^D=\cos \left(\frac{d_{i, j} / \sigma_d}{10000^{2 k / d_t}}\right) \end{array}\right. ⎩ ⎨ ⎧ri,j,2kD=sin(100002k/dtdi,j/σd)ri,j,2k+1D=cos(100002k/dtdi,j/σd)其中 d i , j = ∥ p ^ i − p ^ j ∥ 2 d_{i, j}=\left\|\hat{\mathbf{p}}_i-\hat{\mathbf{p}}_j\right\|_2 di,j=∥p^i−p^j∥2, σ d \sigma_d σd为温度系数
Triplet-Wise Angular Embedding的定义为 , { r i , j , k , 2 x A = sin ( α i , j k / σ a 1000 0 2 x / d t ) r i , j , k , 2 x + 1 A = cos ( α i , j k / σ a 1000 0 2 x / d t ) , , \left\{\begin{array}{rl} r_{i, j, k, 2 x}^A & =\sin \left(\frac{\alpha_{i, j}^k / \sigma_a}{10000^{2 x / d_t}}\right) \\ r_{i, j, k, 2 x+1}^A & =\cos \left(\frac{\alpha_{i, j}^k / \sigma_a}{10000^{2 x / d_t}}\right) \end{array},\right. ,⎩ ⎨ ⎧ri,j,k,2xAri,j,k,2x+1A=sin(100002x/dtαi,jk/σa)=cos(100002x/dtαi,jk/σa),其中 σ a \sigma_a σa为温度系数, α i , j k \alpha_{i, j}^k αi,jk计算方式为获取Super Point p ^ i \hat{\mathbf{p}}_i p^i的 K K K邻域,对于 K K K邻域里的每一个Super Point计算 α i , j x = ∠ ( Δ x , i , Δ j , i ) \alpha_{i, j}^x=\angle\left(\Delta_{x, i}, \Delta_{j, i}\right) αi,jx=∠(Δx,i,Δj,i),其中 Δ i , j : = p ^ i − p ^ j \Delta_{i, j}:=\hat{\mathbf{p}}_i-\hat{\mathbf{p}}_j Δi,j:=p^i−p^j,如下图所示:
最后Geometric Structure Embedding计算如下: r i , j = r i , j D W D + max x { r i , j , x A W A } \mathbf{r}_{i, j}=\mathbf{r}_{i, j}^D \mathbf{W}^D+\max _x\left\{\mathbf{r}_{i, j, x}^A \mathbf{W}^A\right\} ri,j=ri,jDWD+xmax{ri,j,xAWA}整个计算过程流程图如下图所示:

Feature-Bsed Cross-Attention,Cross-Attention部分和正常的Cross-Attention相同的,公式如下: z i P = ∑ j = 1 ∣ Q ∣ a i , j ( x j Q W V ) \mathbf{z}_i^{\mathcal{P}}=\sum_{j=1}^{|\mathcal{Q}|} a_{i, j}\left(\mathbf{x}_j^{\mathcal{Q}} \mathbf{W}^V\right) ziP=j=1∑∣Q∣ai,j(xjQWV) e i , j = ( x i P W Q ) ( x j Q W K ) T d t . e_{i, j}=\frac{\left(\mathbf{x}_i^{\mathcal{P}} \mathbf{W}^Q\right)\left(\mathbf{x}_j^{\mathcal{Q}} \mathbf{W}^K\right)^T}{\sqrt{d_t}} . ei,j=dt(xiPWQ)(xjQWK)T.其中 X P , X Q \mathbf{X}^{\mathcal{P}}, \mathbf{X}^{\mathcal{Q}} XP,XQ为Self-Attention输出特征矩阵。
Superpoint Matching,当Super Point的特征经过多层Self-Attention和Cross-Attention后输出的特征矩阵为 H ^ P \hat{\mathbf{H}}^{\mathcal{P}} H^P 和 H ^ Q \hat{\mathbf{H}}^{\mathcal{Q}} H^Q,首先将 H ^ P \hat{\mathbf{H}}^{\mathcal{P}} H^P 和 H ^ Q \hat{\mathbf{H}}^{\mathcal{Q}} H^Q进行归一化,然后计算Gaussian Correlation Matrix S ∈ R ∣ P ^ ∣ × ∣ Q ^ ∣ \mathbf{S} \in \mathbb{R}^{|\hat{\mathcal{P}}| \times|\hat{\mathbf{Q}}|} S∈R∣P^∣×∣Q^∣ s i , j = exp ( − ∥ h ^ i P − h ^ j Q ∥ 2 2 ) s_{i, j}=\exp \left(-\left\|\hat{\mathbf{h}}_i^{\mathcal{P}}-\hat{\mathbf{h}}_j^{\mathcal{Q}}\right\|_2^2\right) si,j=exp(− h^iP−h^jQ 22)为了进一步抑制模糊匹配,我们对Gaussian Correlation Matrix进行双重归一化操作: s ˉ i , j = s i , j ∑ k = 1 ∣ Q ^ ∣ s i , k ⋅ s i , j ∑ k = 1 ∣ P ^ ∣ s k , j \bar{s}_{i, j}=\frac{s_{i, j}}{\sum_{k=1}^{|\hat{\mathcal{Q}}|} s_{i, k}} \cdot \frac{s_{i, j}}{\sum_{k=1}^{|\hat{\mathcal{P}}|} s_{k, j}} sˉi,j=∑k=1∣Q^∣si,ksi,j⋅∑k=1∣P^∣sk,jsi,j这种抑制可以有效消除错误匹配。最后我们从Gaussian Correlation Matrix S ‾ \overline{\mathbf{S}} S 中选择最大的 N c N_c Nc个对作为Super Point的匹配结果 C ^ = { ( p ^ x i , q ^ y i ) ∣ ( x i , y i ) ∈ topk x , y ( s ˉ x , y ) } \hat{\mathcal{C}}=\left\{\left(\hat{\mathbf{p}}_{x_i}, \hat{\mathbf{q}}_{y_i}\right) \mid\left(x_i, y_i\right) \in \operatorname{topk}_{x, y}\left(\bar{s}_{x, y}\right)\right\} C^={(p^xi,q^yi)∣(xi,yi)∈topkx,y(sˉx,y)}由于GeoTransformer的强大编码能力,这一步获得的匹配结果准确性是很高的,因此这一步不需要RANSAC再做进一步外点去除。
2.3 Point Matching Module
由于Super Point的匹配已经解决了全局的不确定性,在Point级别仅使用通过KPConv Backbone提供的局部特征即可。首先使用一对建立匹配的Super Point关联Patch G x i P \mathcal{G}_{x_i}^{\mathcal{P}} GxiP和Patch G y i Q \mathcal{G}_{y_i}^{\mathcal{Q}} GyiQ点特征构建损失矩阵 C i ∈ R n i × m i \mathbf{C}_i \in \mathbb{R}^{n_i \times m_i} Ci∈Rni×mi C i = F x i P ( F y i Q ) T / d ~ , \mathbf{C}_i=\mathbf{F}_{x_i}^{\mathcal{P}}\left(\mathbf{F}_{y_i}^{\mathcal{Q}}\right)^T / \sqrt{\tilde{d}}, Ci=FxiP(FyiQ)T/d~,其中 n i = ∣ G x i P ∣ , m i = ∣ G y i Q ∣ n_i=\left|\mathcal{G}_{x_i}^{\mathcal{P}}\right|, m_i=\left|\mathcal{G}_{y_i}^{\mathcal{Q}}\right| ni= GxiP ,mi= GyiQ 分别为两个Patch中Point的数量,然后添加新的一列和一行作为Dustbin,最后使用Sinkhorn Algorithm来计算最后的匹配关系,取匹配得分的TopK作为最后Point级别的匹配结果。
以上是针对一对Super Point提取的Point级别的匹配,所有Super Point提取的结果求并集就得到最后全局的Point的匹配结果 C = ⋃ i = 1 N c C i \mathcal{C}=\bigcup_{i=1}^{N_c} \mathcal{C}_i C=⋃i=1NcCi.
2.4 RANSAC-free Local-to-Global Registration
LGR的大致步骤是根据每个Super Point对对应的Patch中的Point的匹配关系都通过SVD计算一个变换矩阵 T i = { R i , t i } \mathbf{T}_i=\left\{\mathbf{R}_i, \mathbf{t}_i\right\} Ti={Ri,ti}: R i , t i = min R , t ∑ ( p ~ x j q ~ y j ) ∈ C i w j i ∥ R ⋅ p ~ x j + t − q ~ y j ∥ 2 2 \mathbf{R}_i, \mathbf{t}_i=\min _{\mathbf{R}, \mathbf{t}} \sum_{\left(\tilde{\mathbf{p}}_{x_j} \tilde{\mathbf{q}}_{y_j}\right) \in \mathcal{C}_i} w_j^i\left\|\mathbf{R} \cdot \tilde{\mathbf{p}}_{x_j}+\mathbf{t}-\tilde{\mathbf{q}}_{y_j}\right\|_2^2 Ri,ti=R,tmin(p~xjq~yj)∈Ci∑wji R⋅p~xj+t−q~yj 22然后使用这些变换矩阵在全局的Point的匹配结果中计算内点: R , t = max R i , t i ∑ ( p ~ x j , q ~ y j ) ∈ C ⟦ ∥ R i ⋅ p ~ x j + t i − q ~ y j ∥ 2 2 < τ a ⟧ \mathbf{R}, \mathbf{t}=\max _{\mathbf{R}_i, \mathbf{t}_i} \sum_{\left(\tilde{\mathbf{p}}_{x_j}, \tilde{\mathbf{q}}_{y_j}\right) \in \mathcal{C}} \llbracket\left\|\mathbf{R}_i \cdot \tilde{\mathbf{p}}_{x_j}+\mathbf{t}_i-\tilde{\mathbf{q}}_{y_j}\right\|_2^2<\tau_a \rrbracket R,t=Ri,timax(p~xj,q~yj)∈C∑[[ Ri⋅p~xj+ti−q~yj 22<τa]]将内点数量最多的变换保留的内点使用上述SVD计算公式进行迭代求解获得最终的匹配结果。
之所以可以实现这样一个Local-to-Global的配准过程是因为作者认为Super Point的匹配结果准确率是非常高的,这样可以节省RANCAC带来的耗时,但是在实际应用过程中如果因为网络训练不充分导致部分场景Super Point的匹配结果都不好,那算法也会整体失效,因此这部分是可以做进一步优化的地方,下面介绍的MAC在这部分就可以发挥作用
2.5 Loss Functions
损失函数主要由两部分构成,分别是用于计算Super Point匹配损失的Overlap-aware Circle Loss L o c \mathcal{L}_{o c} Loc和用于计算Point匹配损失的Point Matching Loss L p \mathcal{L}_p Lp
Overlap-aware Circle Loss,由于Super Point的匹配真值是根据Patch Overlap的结果确定的,因此很有可能出现一对多的匹配结果,如果简单当做一个多标签分类任务使用Cross Entropy Loss进行处理会使得高置信度的正样本被抑制,使得最后预测的Super Point匹配关系不可靠。
为了解决上述问题,作者使用了Overlap-aware Circle Loss,即如果两个Super Point的Patch Overlap比例超过10%,那么就作为正样本,如果不存在Patch Overlap则作为负样本。对于点云 P \mathcal{P} P中的Patch G i P ∈ A \mathcal{G}_i^{\mathcal{P}} \in \mathcal{A} GiP∈A,我们将其对应点云 Q \mathcal{Q} Q中的正样本定义为 ε p i \varepsilon_p^i εpi,负样本定义为 ε n i \varepsilon_n^i εni,则其损失函数为: L o c P = 1 ∣ A ∣ ∑ G i P ∈ A log [ 1 + ∑ G j Q ∈ ε p i e λ i j β p i , j ( d i j − Δ p ) ∑ G k Q ∈ ε n i e β n i , k ( Δ n − d i k ) ] , \mathcal{L}_{o c}^{\mathcal{P}}=\frac{1}{| \mathcal{A}|} \sum_{\mathcal{G}_i^{\mathcal{P}} \in \mathcal{A}} \log \left[1+\sum_{\mathcal{G}_j^{\mathcal{Q}} \in \varepsilon_p^i} e^{\lambda_i^j \beta_p^{i, j}\left(d_i^j-\Delta_p\right)} \sum_{\mathcal{G}_k^Q \in \varepsilon_n^i} e^{\beta_n^{i, k}\left(\Delta_n-d_i^k\right)}\right], LocP=∣A∣1GiP∈A∑log 1+GjQ∈εpi∑eλijβpi,j(dij−Δp)GkQ∈εni∑eβni,k(Δn−dik) ,其中, d i j = ∥ h ^ i P − h ^ j Q ∥ 2 d_i^j=\left\|\hat{\mathbf{h}}_i^{\mathcal{P}}-\hat{\mathbf{h}}_j^{\mathcal{Q}}\right\|_2 dij= h^iP−h^jQ 2为特征空间的距离, λ i j = ( o i j ) 1 2 \lambda_i^j=\left(o_i^j\right)^{\frac{1}{2}} λij=(oij)21代表 G i P \mathcal{G}_i^{\mathcal{P}} GiP和 G i Q \mathcal{G}_i^{\mathcal{Q}} GiQ之间的overlap比例, β p i , j = γ ( d i j − Δ p ) \beta_p^{i, j}=\gamma\left(d_i^j-\Delta_p\right) βpi,j=γ(dij−Δp)和 β n i , k = γ ( Δ n − d i k ) \beta_n^{i, k}=\gamma\left(\Delta_n-d_i^k\right) βni,k=γ(Δn−dik)分别为正样本和负样本的权重, Δ p = 0.1 \Delta_p=0.1 Δp=0.1 和 Δ n = 1.4 \Delta_n=1.4 Δn=1.4为超参数。相同的损失函数 L o c Q \mathcal{L}_{o c}^{\mathcal{Q}} LocQ在点云 Q \mathcal{Q} Q上也计算一边,最后的总损失为 L o c = ( L o c P + L o c Q ) / 2 \mathcal{L}_{o c}=\left(\mathcal{L}_{o c}^{\mathcal{P}}+\mathcal{L}_{o c}^{\mathcal{Q}}\right) / 2 Loc=(LocP+LocQ)/2
Point Matching Loss,在训练阶段随机采样 N g N_g Ng对Super Point匹配真值,对于每个Super Point的匹配 C ^ i ∗ \hat{\mathcal{C}}_i^* C^i∗会在半径 τ \tau τ内提取一系列真值点的匹配 M i \mathcal{M}_i Mi,对于Patch内没有匹配上的点记为 I i \mathcal{I}_i Ii 和 J i \mathcal{J}_i Ji,那么最后的损失函数为: L p , i = − ∑ ( x , y ) ∈ M i log z ˉ x , y i − ∑ x ∈ I i log z ˉ x , m i + 1 i − ∑ y ∈ J i log z ˉ n i + 1 , y i , \mathcal{L}_{p, i}=-\sum_{(x, y) \in \mathcal{M}_i} \log \bar{z}_{x, y}^i-\sum_{x \in \mathcal{I}_i} \log \bar{z}_{x, m_i+1}^i-\sum_{y \in \mathcal{J}_i} \log \bar{z}_{n_i+1, y}^i, Lp,i=−(x,y)∈Mi∑logzˉx,yi−x∈Ii∑logzˉx,mi+1i−y∈Ji∑logzˉni+1,yi,最后的损失函数为所有Super Point匹配结果的平均值: L p = 1 N g ∑ i = 1 N g L p , i \mathcal{L}_p=\frac{1}{N_g} \sum_{i=1}^{N_g} \mathcal{L}_{p, i} Lp=Ng1∑i=1NgLp,i。以上就完成了GeoTransformer的基本内容介绍,下面补充下Circle Loss和Metrics相关的知识
2.6 Circle Loss
Circle Loss是在度量学习任务中提出的一种Loss,度量学习的目标是相似或者属于同一类样本提取到的embedding向量之间具备更高的相似度或者更小的空间距离,像人脸识别、图像检索这样的任务都属于度量学习。
在Circle Loss之前的损失函数式通过训练使得positive之间的相似度 s p s_p sp大于positive和negative之间的相似度 s n s_n sn,损失函数定义为 max { 0 , s n + m − s p } \max \left\{0, s_n+m-s_{\mathrm{p}}\right\} max{0,sn+m−sp},其中控制分离度的参数 m m m为超参数,该损失函数的优化方向要么是增大 s p s_p sp要么是减小 s n s_n sn,该损失函数定义的目标是正确的,但问题如下图(a)所示,在相同的控制参数 m m m的影响下, A A A、 B B B、 C C C三个点可能被优化到目标边界上任意一点,即 T T T或者 T ′ T^{\prime} T′点,这样会导致优化目标不明确

而Circle Loss则是将目标边界调整为了如图(b)所示,这样的目标边界将 A A A、 B B B、 C C C都往点 T T T进行优化,目标明确,效果更高,这里我们来简单看到Circle Loss的推导过程:
Circle Loss的论文中提出的基础版本的Loss如下所示: L u n i = log [ 1 + ∑ i = 1 K ∑ j = 1 L exp ( γ ( s n j − s p i + m ) ) ] = log [ 1 + ∑ j = 1 L exp ( γ ( s n j + m ) ) ∑ i = 1 K exp ( γ ( − s p i ) ) ] L_{u n i}=\log \left[1+\sum_{i=1}^K \sum_{j=1}^L \exp \left(\gamma\left(s_n^j-s_p^i+m\right)\right)\right]=\log \left[1+\sum_{j=1}^L \exp \left(\gamma\left(s_n^j+m\right)\right) \sum_{i=1}^K \exp \left(\gamma\left(-s_p^i\right)\right)\right] Luni=log[1+i=1∑Kj=1∑Lexp(γ(snj−spi+m))]=log[1+j=1∑Lexp(γ(snj+m))i=1∑Kexp(γ(−spi))]其中, γ \gamma γ起到损失函数尺度缩放作用。 K K K表示与输入特征向量 x x x具备相同ID的样本个数, L L L表示与输入特征向量具备不同ID的样本个数,即positive样本为 { s p i } ( i = 1 , 2 , ⋯ , K ) \left\{s_p^i\right\}(i=1,2, \cdots, K) {spi}(i=1,2,⋯,K),negative样本为 { s n i } ( i = 1 , 2 , ⋯ , L ) \left\{s_n^i\right\}(i=1,2, \cdots, L) {sni}(i=1,2,⋯,L)。
Circle Loss认为离最优值越远的样本应该具备更更大的优化权重,因此对 s p s_p sp和 s n s_n sn分别进行独立加权,将优化目标修改为 α n s n + m − α p s p ≤ 0 \alpha_n s_n+m-\alpha_p s_{\mathrm{p}} \leq 0 αnsn+m−αpsp≤0,其中 α n j \alpha_n^j αnj 和 α p i \alpha_p^i αpi为自主学习得到的权重参数用于控制 s n s_n sn 和 s p s_p sp的学习步长,因此Circle Loss的定义为: L circle = log [ 1 + ∑ i = 1 K ∑ j = 1 L exp ( γ ( α n j s n j − α p i s p i ) ) ] = log [ 1 + ∑ j = 1 L exp ( γ α n j s n j ) ∑ i = 1 K exp ( − γ α p i s p i ) ] L_{\text {circle }}=\log \left[1+\sum_{i=1}^K \sum_{j=1}^L \exp \left(\gamma\left(\alpha_n^j s_n^j-\alpha_p^i s_p^i\right)\right)\right]=\log \left[1+\sum_{j=1}^L \exp \left(\gamma \alpha_n^j s_n^j\right) \sum_{i=1}^K \exp \left(-\gamma \alpha_p^i s_p^i\right)\right] Lcircle =log[1+i=1∑Kj=1∑Lexp(γ(αnjsnj−αpispi))]=log[1+j=1∑Lexp(γαnjsnj)i=1∑Kexp(−γαpispi)]其中 { α p i = [ O p − s p i ] + α n j = [ s n j − O n ] + \left\{\begin{array}{l} \alpha_p^i=\left[O_p-s_p^i\right]_{+} \\ \alpha_n^j=\left[s_n^j-O_n\right]_{+} \end{array}\right. {αpi=[Op−spi]+αnj=[snj−On]+其中假设 s n s_n sn 和 s p s_p sp的最优值分别为 O n O_n On 和 O p O_p Op,上述公式的含义是当 s p i ≥ O p s_p^i \geq O_p spi≥Op时,说明得到的 s p s_p sp已经足够好,不需要再进行惩罚, s n j s_n^j snj同理。我们将控制分离度的参数对于 s n s_n sn 和 s p s_p sp进行解耦,则Circle Loss进一步演变为 L circle = log [ 1 + ∑ j = 1 L exp ( γ α n j s n j − Δ n ) ∑ i = 1 K exp ( − γ α p i s p i − Δ p ) ] L_{\text {circle }}=\log \left[1+\sum_{j=1}^L \exp \left(\gamma \alpha_n^j s_n^j-\Delta_n\right) \sum_{i=1}^K \exp \left(-\gamma \alpha_{p}^i s_p^i-\Delta_p\right)\right] Lcircle =log[1+j=1∑Lexp(γαnjsnj−Δn)i=1∑Kexp(−γαpispi−Δp)]为了简单起见,作者将 O p 、 O n 、 Δ n O_p 、 O_n 、 \Delta_n Op、On、Δn 和 Δ p \Delta_p Δp分别设置为: O p = 1 + m O_p=1+m Op=1+m O n = − m O_n=-m On=−m Δ n = m \Delta_n=m Δn=m Δ p = 1 − m \Delta_p=1-m Δp=1−m其中 m ∈ [ 0 , 1 ] , s p i > 1 − m , s n j < m m \in[0,1], s_p^i>1-m, \quad s_n^j<m m∈[0,1],spi>1−m,snj<m, m m m越小对于训练集要求得到的预测置信度越高,在训练集上的你和程度越高,对于数据的泛化能力相对变差。经过简化,Circle Loss的超参数就只有 γ \gamma γ和 m m m两个了
回到GeoTransformer,可以看到Overlap Circle Loss是在Circle Loss的基础上在正样本项上增加了一个表示overlap比例的权重,使得模型更加关注overlap高的匹配样本。
2.7 Metrics
最后我们看下GeoTransformer对齐训练结果的评测方法,对于3DMatch和KITTI两个数据集作者定义了两类不同的评测指标。
2.7.1 Inlier Ratio、Feature Matching Recall、Registration Recall
Inlier Ratio、Feature Matching Recall、Registration Recall这三个指标是针对3DMatch数据集定义的
Inlier Ratio定义的是正确的匹配对相对于总匹配对的比例,其中两个点之间的距离小于10cm定义为正确的匹配对,具体公式如下: IR = 1 ∣ C ∣ ∑ ( p x i , q y i ) ∈ C ⟦ ∥ T ‾ P → Q ( p x i ) − q y i ∥ 2 < τ 1 ⟧ , \operatorname{IR}=\frac{1}{|\mathcal{C}|} \sum_{\left(\mathbf{p}_{x_i}, \mathbf{q}_{y_i}\right) \in \mathcal{C}} \llbracket\left\|\overline{\mathbf{T}}_{\mathbf{P} \rightarrow \mathbf{Q}}\left(\mathbf{p}_{x_i}\right)-\mathbf{q}_{y_i}\right\|_2<\tau_1 \rrbracket, IR=∣C∣1(pxi,qyi)∈C∑[[ TP→Q(pxi)−qyi 2<τ1]],
Feature Matching Recall定义的是Inlier Ratio值高于0.05的匹配点云的数量: F M R = 1 M ∑ i = 1 M ⟦ I R i > τ 2 ⟧ \mathrm{FMR}=\frac{1}{M} \sum_{i=1}^M \llbracket \mathrm{IR}_i>\tau_2 \rrbracket FMR=M1i=1∑M[[IRi>τ2]]其中 M M M为所有的点云对数量
Registration Recall定义的是正确匹配的点云对的数量,其中正确匹配的定义是最后求解的变化误差小于0.2m: RMSE = 1 ∣ C ∗ ∣ ∑ ( p x i ∗ , q y i ∗ ) ∈ C ∗ ∥ T P → Q ( p x i ∗ ) − q y i ∗ ∥ 2 2 , \operatorname{RMSE}=\sqrt{\frac{1}{\left|\mathcal{C}^*\right|} \sum_{\left(\mathbf{p}_{x_i}^*, \mathbf{q}_{y_i}^*\right) \in \mathcal{C}^*}\left\|\mathbf{T}_{\mathbf{P} \rightarrow \mathbf{Q}}\left(\mathbf{p}_{x_i}^*\right)-\mathbf{q}_{y_i}^*\right\|_2^2}, RMSE=∣C∗∣1(pxi∗,qyi∗)∈C∗∑ TP→Q(pxi∗)−qyi∗ 22, R R = 1 M ∑ i = 1 M ⟦ R M S E i < 0.2 m ⟧ \mathrm{RR}=\frac{1}{M} \sum_{i=1}^M \llbracket \mathrm{RMSE}_i<0.2 \mathrm{~m} \rrbracket RR=M1i=1∑M[[RMSEi<0.2 m]]
2.7.2 Relative Rotation Error、Relative Translation Error、Registration Recall
Relative Rotation Error定义为真值和预测结果之间的角度误差 R R E = arccos ( trace ( R T ⋅ R ‾ − 1 ) 2 ) \mathrm{RRE}=\arccos \left(\frac{\operatorname{trace}\left(\mathbf{R}^T \cdot \overline{\mathbf{R}}-1\right)}{2}\right) RRE=arccos(2trace(RT⋅R−1))
Relative Translation Error定义为真值和预测结果之间的平移误差 R T E = ∥ t − t ‾ ∥ 2 . \mathrm{RTE}=\|\mathbf{t}-\overline{\mathbf{t}}\|_2 . RTE=∥t−t∥2.
Registration Recall定义为Relative Rotation Error和Relative Translation Error都小于一定阈值比例 R R = 1 M ∑ i = 1 M ⟦ R R E i < 5 ∘ ∧ R T E i < 2 m ⟧ \mathrm{RR}=\frac{1}{M} \sum_{i=1}^M \llbracket \mathrm{RRE}_i<5^{\circ} \wedge \mathrm{RTE}_i<2 \mathrm{~m} \rrbracket RR=M1i=1∑M[[RREi<5∘∧RTEi<2 m]]
3. MAC
MAC发表于2023年CVPR,原论文为《3D Registration with Maximal Cliques》,本文的主要贡献是优化了极大团的构建策略,使得点云匹配的速度、性能显著提升。极大团的概念并不是本提出的,在之前已经有很多研究人员研究该问题,本文提出了一个较高的解决方案。
3.1 Graph Construction
对于两块待匹配的点云 P s \mathbf{P}^s Ps和 P t \mathbf{P}^t Pt,初始的匹配关系 C initial = { c } \mathbf{C}_{\text {initial }}=\{\mathbf{c}\} Cinitial ={c}通过特征描述子获得,其中 c = ( p s , p t ) \mathbf{c}=\left(\mathbf{p}^s, \mathbf{p}^t\right) c=(ps,pt), p s \mathbf{p}^s ps和 p t \mathbf{p}^t pt分别为点云 P s \mathbf{P}^s Ps和 P t \mathbf{P}^t Pt中的点。MAC就是通过构建Graph从 C initial \mathbf{C}_{\text {initial }} Cinitial 中获得点云 P s \mathbf{P}^s Ps和 P t \mathbf{P}^t Pt的位姿变换。
Fisrt Order Graph的构建主要基于匹配点对 ( c i , c j ) \left(\mathbf{c}_i, \mathbf{c}_j\right) (ci,cj)之间的刚性距离限制 S d i s t ( c i , c j ) = ∣ ∥ p i s − p j s ∥ − ∥ p i t − p j t ∥ ∣ S_{d i s t}\left(\mathbf{c}_i, \mathbf{c}_j\right)=\left|\left\|\mathbf{p}_i^s-\mathbf{p}_j^s\right\|-\left\|\mathbf{p}_i^t-\mathbf{p}_j^t\right\|\right| Sdist(ci,cj)= pis−pjs − pit−pjt 这其实很好理解,因为点云本身和点云匹配的过程都是刚性的。基于该限制我们计算匹配点对之间点对得分为: S c m p ( c i , c j ) = exp ( − S d i s t ( c i , c j ) 2 2 d c m p 2 ) S_{c m p}\left(\mathbf{c}_i, \mathbf{c}_j\right)=\exp \left(-\frac{S_{d i s t}\left(\mathbf{c}_i, \mathbf{c}_j\right)^2}{2 d_{c m p}^2}\right) Scmp(ci,cj)=exp(−2dcmp2Sdist(ci,cj)2)其中 d c m p d_{c m p} dcmp,可以看到 S dist ( c i , c j ) S_{\text {dist }}\left(\mathbf{c}_i, \mathbf{c}_j\right) Sdist (ci,cj)越小得分越高越接近于1,而 S dist ( c i , c j ) S_{\text {dist }}\left(\mathbf{c}_i, \mathbf{c}_j\right) Sdist (ci,cj)过大则会导致得分几乎为零。由于没有方向,Fisrt Order Graph W F O G \mathbf{W}_{F O G} WFOG是一个对称矩阵。
Second Order Graph是基于Fisrt Order Graph构建的稀疏矩阵: W S O G = W F O G ⊙ ( W F O G × W F O G ) \mathbf{W}_{S O G}=\mathbf{W}_{F O G} \odot\left(\mathbf{W}_{F O G} \times \mathbf{W}_{F O G}\right) WSOG=WFOG⊙(WFOG×WFOG)相对于Fisrt Order Graph,Second Order Graph具备的优势是具备更严格边构建条件并且更稀疏,有助于更快地搜索团。Fisrt Order Graph和Second Order Graph的区别如下图所示:

3.2 Search Maximal Cliques
给定一个无向图 G = ( V , E ) G=(\mathbf{V}, \mathbf{E}) G=(V,E),团的定义为 C = ( V ′ , E ′ ) C=\left(\mathbf{V}^{\prime}, \mathbf{E}^{\prime}\right) C=(V′,E′),其中 V ′ ⊆ V , E ′ ⊆ E \mathbf{V}^{\prime} \subseteq \mathbf{V}, \mathbf{E}^{\prime} \subseteq \mathbf{E} V′⊆V,E′⊆E, C C C是 G G G的子集。最大团的定义就是无向图中拥有最多节点的团。
之前有很多工作在研究如何从一个无向图中搜索出最大团,他是他们的问题是搜索过程集中在无向图中的全局信息,而本文放松了这种限制使得搜索最大团的过程可以更加关注局部信息。具体方法如下:
Node-guided Clique Selection在初始的最大团搜索后得到 M A C initial M A C_{\text {initial }} MACinitial ,我们赋予每一个团 C i = ( V i , E i ) C_i=\left(\mathbf{V}_i, \mathbf{E}_i\right) Ci=(Vi,Ei)一个权重 w C i w_{C_i} wCi,权重的计算方式为: w C i = ∑ e j ∈ E i w e j w_{C_i}=\sum_{e_j \in \mathbf{E}_i} w_{e_j} wCi=ej∈Ei∑wej其中 w e j w_{e_j} wej为 W S O G \mathbf{W}_{S O G} WSOG中的边权 e j e_j ej,一个node可能会被多个团所包含,我们采用的策略是将该node保留在权重最大的团中,其他权重偏低团将会被移除,剩下的团记为 M A C selected MAC_{\text {selected }} MACselected ,接下来我们对 M A C selected MAC_{\text {selected }} MACselected 进行进一步过滤,过滤逻辑如下:
- Normal Consistency 指的是给定两个匹配对 c i = ( p i s , p i t ) , c j = ( p j s , p j t ) \mathbf{c}_i=\left(\mathbf{p}_i^s, \mathbf{p}_i^t\right), \mathbf{c}_j=\left(\mathbf{p}_j^s, \mathbf{p}_j^t\right) ci=(pis,pit),cj=(pjs,pjt)以及这四个点构成的向量 n i s , n j s , n i t , n j t \mathbf{n}_i^s, \mathbf{n}_j^s, \mathbf{n}_i^t, \mathbf{n}_j^t nis,njs,nit,njt,他们的角度差分别为 α i j s = ∠ ( n i s , n j s ) , α i j t = ∠ ( n i t , n j t ) \alpha_{i j}^s=\angle\left(\mathbf{n}_i^s, \mathbf{n}_j^s\right), \alpha_{i j}^t=\angle\left(\mathbf{n}_i^t, \mathbf{n}_j^t\right) αijs=∠(nis,njs),αijt=∠(nit,njt),他们的角度差不应该过,即 ∣ sin α i j s − sin α i j t ∣ < t α \left|\sin \alpha_{i j}^s-\sin \alpha_{i j}^t\right|<t_\alpha sinαijs−sinαijt <tα其中 t α t_\alpha tα为超参数阈值。
- Clique Ranking指的是对 M A C selected MAC_{\text {selected }} MACselected 按照权重 w C i w_{C_i} wCi进行排序,Top-K的应该被保留。
经过上述操作,原本数量非常巨大的 M A C initial M A C_{\text {initial }} MACinitial 会减小到一定数量,最后通过Instance-equal SVD或者Weighted SVD就可以求解最后的变换。
我觉得很棒的一点是MAC可以作为模块添加到其他方法中,我们可以看到加入MAC后各个方法的指标都有明显提高:

相关文章:

激光点云配准算法——Cofinet / GeoTransforme / MAC
激光点云配准算法——Cofinet / GeoTransformer / MAC GeoTransformer MAC是当前最SOTA的点云匹配算法,在之前我用总结过视觉特征匹配的相关算法 视觉SLAM总结——SuperPoint / SuperGlue 本篇博客对Cofinet、GeoTransformer、MAC三篇论文进行简单总结 1. Cofine…...

socket--cs--nc简单实现反弹shell
socket_client.py import socket#客户端: #连接服务段的地址和端口 #输入命令发送执行 #回显命令执行结果# ipinput(please input connect ip:) # portinput(please input connect port:)ssocket.socket() # IP and PORT s.connect((,9999)) while True:cmdlineinput(please i…...

CSS入门基础2
目录 1.标签类型 2.块元素 3.行内元素 4.行内块元素 5.标签行内转换 6.背景样式 1.标签类型 标签以什么方式进行显示,比如div 自己占一行, 比如span 一行可以放很多个HTML标签一般分为块标签和行内标签两种类型: 块元素行内元素。 2.块…...
Mac vscode could not import github.com/gin-gonic/gin
问题背景: 第一次导入一个go的项目就报红 问题分析: 其实就是之前没有下载和导入gin这个web框架包 gin是一个golang的微框架,封装比较优雅,API友好,源码注释比较明确。 问题解决: 依次输入以下命令。通…...

MySQL修改用户权限(宝塔)
在我们安装好的MySQL中,很可能对应某些操作时,不具备操作的权限,如下是解决这些问题的方法 我以宝塔创建数据库为例,创建完成后,以创建的用户名和密码登录 这里宝塔中容易发生问题的地方,登录不上去&#…...
Sparse PCA: A Geometric Approach)
论文阅读(一种新的稀疏PCA求解方式)Sparse PCA: A Geometric Approach
这是一篇来自JMLR的论文,论文主要关注稀疏主成分分析(Sparse PCA)的问题,提出了一种新颖的几何解法(GeoSPCA)。 该方法相比传统稀疏PCA的解法的优点:1)更容易找到全局最优ÿ…...
Chrome/Edge浏览器视频画中画可拉动进度条插件
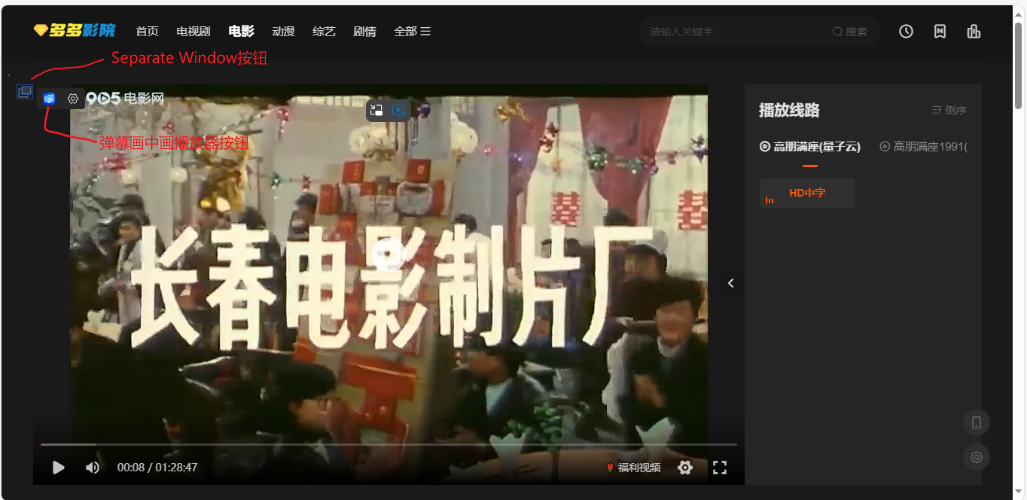
目录 前言 一、Separate Window 忽略插件安装,直接使用 注意事项 插件缺点 1 .无置顶功能 2.保留原网页,但会刷新原网页 3.窗口不够美观 二、弹幕画中画播放器 三、失败的尝试 三、Potplayer播放器 总结 前言 平时看一些视频的时候ÿ…...

pg修炼之道学习笔记
一、数据库逻辑结构介绍 1、一个pg数据库服务下有多个db(多个数据库),当应用连接到一个数据库时,一般只能访问这个数据库中的数据,而不能访问其他数据库的内容(限制) 2、表索引:一…...

使用宝塔面板部署Django应用(不成功Kill Me!)
使用宝塔面板部署Django应用 文章目录 使用宝塔面板部署Django应用 本地操作宝塔面板部署可能部署失败的情况 本地操作 备份数据库 # 备份数据库 mysqldump -u root -p blog > blog.sql创建requirements # 创建requirements.txt pip freeze > requirements.txt将本项目…...

c++深拷贝、浅拷贝
在 C 中,深拷贝和浅拷贝是两个重要的概念,尤其在涉及动态内存分配和指针成员时。这两个概念描述了对象复制时的行为。 浅拷贝 浅拷贝是指复制对象时,仅复制对象的基本数据成员,对于指针成员,只复制指针地址ÿ…...

k8s核心组件
Master组件: kube-apiserver:用于暴露Kubernetes API,任何资源请求或调用操作都是通过kube-apiserver提供的接口进行。它是Kubernetes集群架构的大脑,负责接收所有请求,并根据用户的具体请求通知其他组件工作。etcd&am…...

反编译腾讯vmp
反编译腾讯vmp 继续学习的过程 多翻译几个vmp 学习 看看他们的是怎么编译的 写一个自己的vmp function __TENCENT_CHAOS_VM(U, T, g, D, j, E, K, w) {// U指令起点// T是指令list// g是函数this 或window对象// D是内部变量和栈}for (0; ;)try {for (var B !1; !B;) {let no…...

Ollama:本地部署大模型 + LobeChat:聊天界面 = 自己的ChatGPT
本地部署大模型 在本地部署大模型有多种方式,其中Ollama方式是最简单的,但是其也有一定的局限性,比如大模型没有其支持的GGUF二进制格式,就无法使用Ollama方式部署。 GGUF旨在实现快速加载和保存大语言模型,并易于阅读…...

JS中splice怎么使用
在JavaScript中,splice() 是一个数组方法,用于添加/删除项目,并返回被删除的项目。这个方法会改变原始数组。 splice() 方法的基本语法如下: array.splice(start[, deleteCount[, item1[, item2[, ...]]]]) start(必…...
Flutter项目,Xcode15, 编译正常,但archive报错
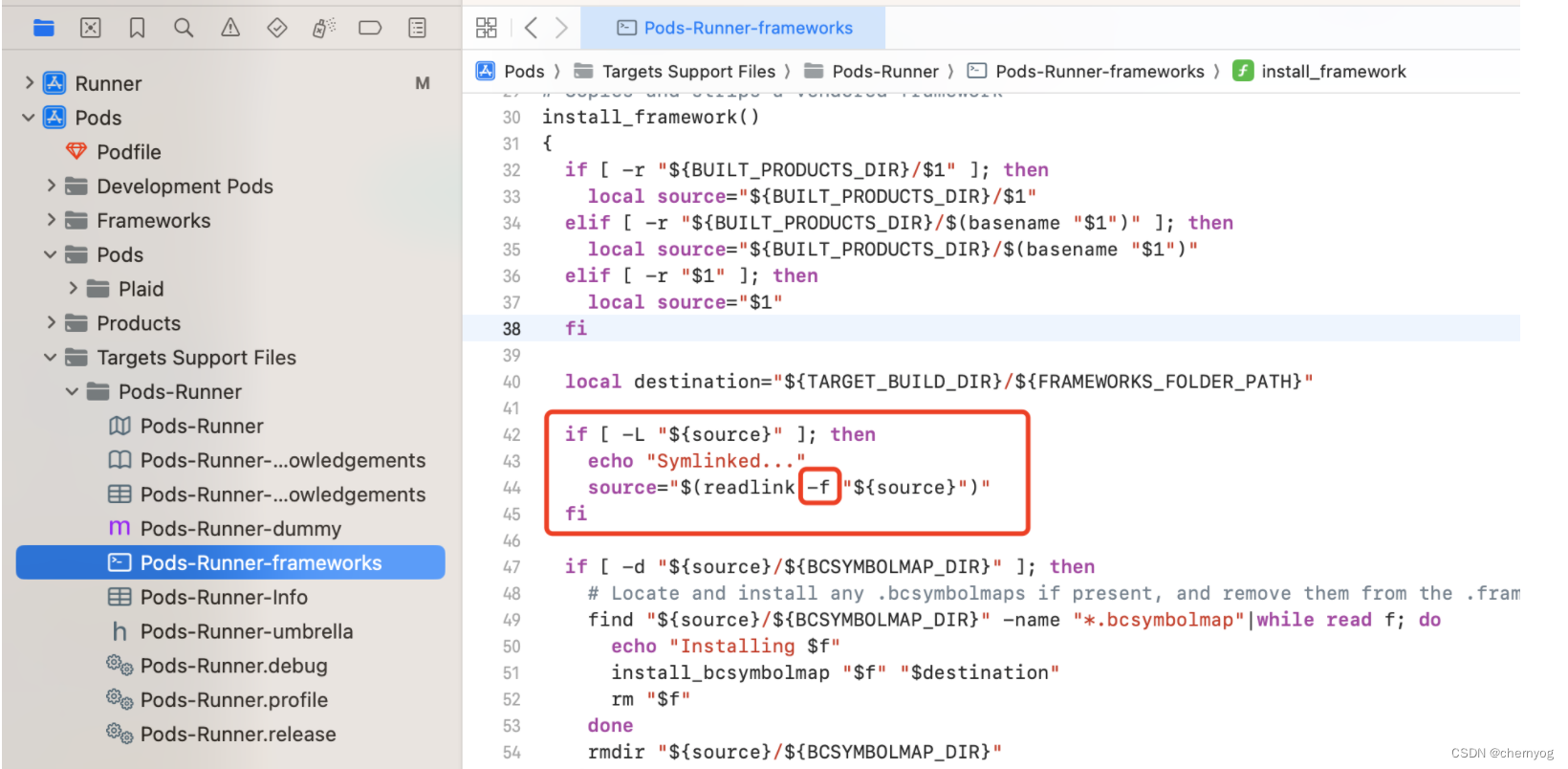
错误提示 PhaseScriptExecution [CP]\ Embed\ Pods\ Frameworks /Users/目录/Developer/Xcode/DerivedData/Runner-brgnkruocugbipaswyuwsjsnqkzm/Build/Intermediates.noindex/ArchiveIntermediates/Runner/IntermediateBuildFilesPath/Runner.build/Release-iphoneos/Runner…...

云动态摘要 2024-06-17
给您带来云厂商的最新动态,最新产品资讯和最新优惠更新。 最新优惠与活动 [低至1折]腾讯混元大模型产品特惠 腾讯云 2024-06-06 腾讯混元大模型产品特惠,新用户1折起! 云服务器ECS试用产品续用 阿里云 2024-04-14 云服务器ECS试用产品续用…...

【JavaScript脚本宇宙】图像处理新纪元:探索六大JavaScript图像处理库
揭开图像处理的奥秘:六款顶级JavaScript库详解 前言 在现代Web开发中,图像处理变得越来越重要。从图像比较到图像编辑,每个步骤都需要高效、强大的工具来完成。JavaScript生态系统为开发者提供了丰富的图像处理库,这些库不仅功能…...

使用python调ffmpeg命令将wav文件转为320kbps的mp3
320kbps竟然是mp3的最高采样率,有点低了吧。 import os import subprocessif __name__ __main__:work_dir "D:\\BaiduNetdiskDownload\\周杰伦黑胶\\魔杰座" fileNames os.listdir(work_dir)for filename in fileNames:pure_name, _ os.path.spli…...

程序启动 报错 no main manifest attribute
1、报错问题 未找到启动类 2、可能的原因 启动没加注解maven打包插件没有设置...

java-内部类 2
### 8. 内部类的访问规则和限制 #### 8.1 访问外部类的成员 内部类可以直接访问外部类的成员变量和方法,包括私有成员。例如: java class OuterClass { private String outerField "Outer field"; class InnerClass { void di…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

UE5 音效系统
一.音效管理 音乐一般都是WAV,创建一个背景音乐类SoudClass,一个音效类SoundClass。所有的音乐都分为这两个类。再创建一个总音乐类,将上述两个作为它的子类。 接着我们创建一个音乐混合类SoundMix,将上述三个类翻入其中,通过它管理每个音乐…...
