redis持久化方式—RDB
RDB快照
与AOF记录写操作命令不同,RDB直接记录内存中的二进制数据,reids恢复数据时,直接将RDB文件加载到内存中就可以了,听起来是不是RDB完虐AOF?那么看完本文,会让你的态度转变,因为RDB的缺点比AOF更糟糕
RDB快照怎么用?
Redis 提供了两个命令来生成 RDB 文件,分别是 save 和 bgsave,他们的区别就在于是否在「主线程」里执行:
- 执行了 save 命令,就会在主线程生成 RDB 文件,由于和执行操作命令在同一个线程,所以如果写入 RDB 文件的时间太长,会阻塞主线程;
- 执行了 bgsave 命令,会创建一个子进程来生成 RDB 文件,这样可以避免主线程的阻塞;
RDB 文件的加载工作是在服务器启动时自动执行的,Redis 并没有提供专门用于加载 RDB 文件的命令。
Redis 还可以通过配置文件的选项来实现每隔一段时间自动执行一次 bgsave 命令,默认会提供以下配置:
save 900 1
save 300 10
save 60 10000
别看选项名叫 save,实际上执行的是 bgsave 命令,也就是会创建子进程来生成 RDB 快照文件。
只要满足上面条件的任意一个,就会执行 bgsave,它们的意思分别是:
- 900 秒之内,对数据库进行了至少 1 次修改;
- 300 秒之内,对数据库进行了至少 10 次修改;
- 60 秒之内,对数据库进行了至少 10000 次修改。
看上去RDB 和 AOF 有几点相似之处:
1.都有在主进程、子进程进行持久化的方式
2.主进程中的持久化操作和主进程的其它操作是串行的,有阻塞主进程的风险
3.fork出子进程进程持久化势必会出现持久化过程中主进程添加新数据而造成父子进程数据不一致的问题
注意
前文没有详细说明,RDB快照是全量快照,也就是说每次执行save或bgsave命令会将当前数据库的全部内存数据进行记录
现在,聪明的你,发现RDB的致命缺陷了吗?
RDB的致命缺陷
1.由于RDB是对数据库当前内存数据的全量快照,势必造成前后两次生成的RDB文件有重复部分,并且重复的数量会越来越大
2.全量快照导致了,RDB文件会随数据库的体积增大而增大,在生成较大RDB文件时会对redis造成性能影响,这也是RDB需要使用bgsave在子进程中持久化的原因
3.正是由于生成较大体积的RDB文件的开销较大,因此RDB操作不能像AOF那样频繁,因此RDB有持久化的窗口期,会造成数据丢失的风险,而相比之下,AOF安全的多
说说bgsave的问题
bgsave创建一个子进程,进行RDB持久化操作,与AOF类似,子进程只拥有fork时刻的父进程数据库状态,在子进程持久化过程中新加入到父进程的数据,在子进程中是没有的,这部分数据只能在下一次RDB时进行持久化,如果在下一次RDB前redis宕机,那么这部分数据就会丢失,这部分丢失的数据是比AOF要多的,因为RDB对新数据的持久化频率远低于AOF
终极方案——RDB+AOF混合持久化
我在“AOF持久化”的文章中介绍到,AOF有解决持久化过程中由于新数据的加入,造成父子进程数据不一致而导致的数据丢失方案————持久化过程中,将新数据追加到父进程、子进程,从而实现数据同步
但RDB不同,由于RDB是对数据库的全量快照,没有用到AOF所使用的缓冲区,那么持久化过程中的新数据丢失问题就没办法解决了吗?
解决方案是AOF
如果想要开启混合持久化功能,可以在 Redis 配置文件将下面这个配置项设置成 yes:
aof-use-rdb-preamble yes
混合持久化工作在 AOF 日志重写过程。
开启了混合持久化后,在AOF使用fork创建子进程来进行AOF重写时,不再将数据库中的内存数据转换成命令,而是像RDB一样,直接将内存数据以RDB格式写入到FOD文件中,在这个过程中,父进程新加入的数据也会追加到AOF子进程的aof重写缓冲区内,这部分数据是AOF格式,写入完成后通知主进程将新的含有 RDB 格式和 AOF 格式的 AOF 文件替换旧的的 AOF 文件。
也就是说,使用了混合持久化,AOF 文件的前半部分是 RDB 格式的全量数据,后半部分是 AOF 格式的增量数据。
混合持久化对AOF和RDB的优化:
1.混合持久化优化了AOF重写时,将数据库的内存数据转换成命令的这个过程,实际上将内存数据转换成命令这步操作是冗余的,AOF重写之所以进行这个转换,是为了保证AOF文件格式的一致性,
而混合持久化的AOF文件中有RDB和AOF两种文件格式,避免了将内存数据转换成命令的步骤,提高了持久化效率
2.RDB在bgsave持久化过程中父进程添加的新数据有丢失的风险,且没有手段规避(AOF遇到同样的问题有解决方案),而混合持久化将RDB有丢失风险的这部分数据,采用了AOF的方案:追加命令到子进程的aof重写缓冲区,并以aof格式保存
总结
混合持久化的方案结合了RDB的快速加载、AOF的数据安全(数据丢失少)的优点,一定程度规避了RDB的易丢失数据、AOF加载慢的缺点
重启 Redis 加载数据的时候,由于前半部分是 RDB 内容,这样加载的时候速度会很快。
加载完 RDB 的内容后,才会加载后半部分的 AOF 内容,这里的内容是 Redis 后台子进程重写 AOF 期间,主线程处理的操作命令,可以使得数据更少的丢失
推荐学习 https://xxetb.xetslk.com/s/p5Ibb
相关文章:

redis持久化方式—RDB
RDB快照 与AOF记录写操作命令不同,RDB直接记录内存中的二进制数据,reids恢复数据时,直接将RDB文件加载到内存中就可以了,听起来是不是RDB完虐AOF?那么看完本文,会让你的态度转变,因为RDB的缺点…...
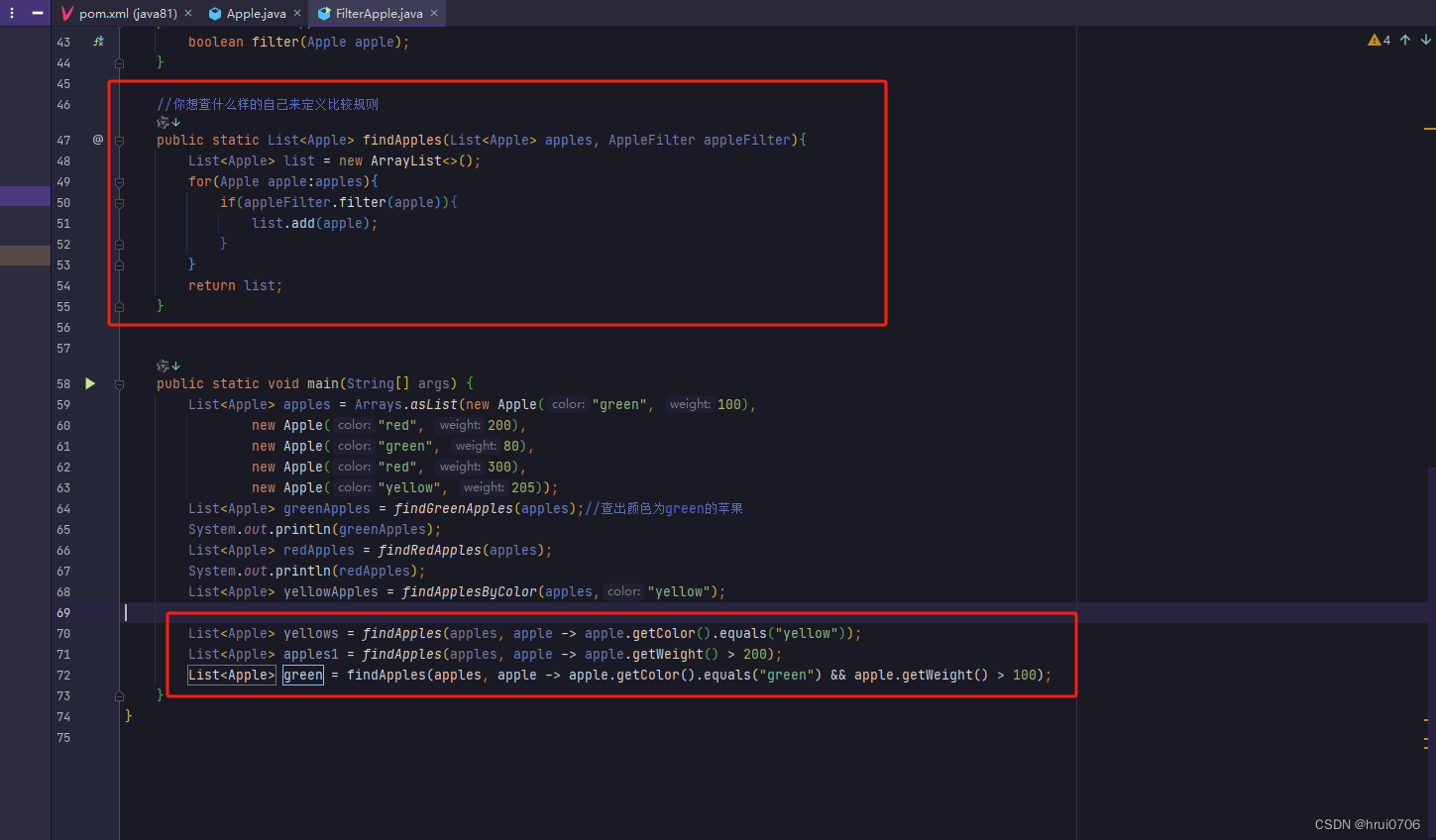
java8实战1(让方法参数具备行为能力)
客户需求是查出颜色为green的苹果 客户需求变成查出颜色为red的苹果 假设现在客户需求又变了,找出黄色的呢?你想查什么颜色直接做为参数输入 让调用者输入颜色参数 问题是现在客户想把重量做为条件,来筛选苹果集合 这就为难了,客户需求随时会变 观察以上例子,发现有个共同…...
C#(C Sharp)学习笔记_多态【十九】
前言 个人觉得多态在面向对象编程中还比较重要的,而且不容易理解。也是学了一个下午,才把笔记写得相对比较完善,但仍欠缺一些内容。慢慢来吧…… 什么是多态? 基本概念 在编程语言和类型论中,多态(Poly…...
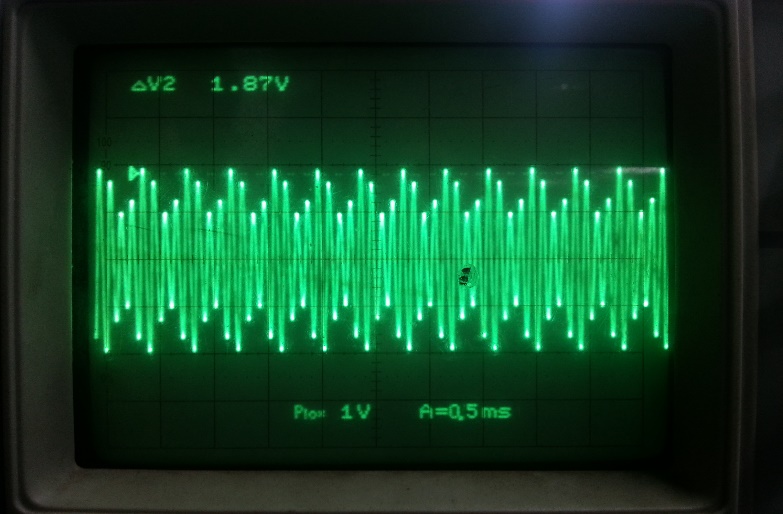
电子竞赛1——基于DDS的AM信号发生器
课题要求 产生AM调幅波; 要求:载波10K,被调制波1K; 短按键1(pin_143)改变该调幅波的调制度:25%、50%、75%; 长按按键1(pin_143)改变被调制信号频率&#…...
CentOS7的#!bash #!/bin/bash #!/bin/env bash #!/usr/bin/bash #!/usr/bin/env bash
bash脚本开头可写成 #!/bin/bash , #!/bin/env bash , #!/usr/bin/bash , #!/usr/bin/env bash #!/bin/bash , #!/usr/bin/bash#!/bin/env bash , #!/usr/bin/env bash CentOS7的 /bin 是 /usr/bin 的软链接, /sbin 是 /usr/sbin 的软链接, [root3050 ~]# ll /bin lrwxrwxrw…...

代码随想录第四十一天打卡
01背包问题 二维 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili #include <iostream> #include <vector>…...

矩阵补全IGMC 学习笔记
目录 Inductive Graph-based Matrix Completion (IGMC) 模型 igmc推理示例: Inductive Graph-based Matrix Completion (IGMC) 模型 原版代码: IGMC/models.py at master muhanzhang/IGMC GitHub GNN推理示例 torch_geometric版本:tor…...

面试题之CSS
1. 引入样式的方式 外部样式 link import 区别 内部样式 /* 写在头部标签 */ <style></style>行内样式 2. 三行代码画三角形 .triangle{width:0px;border:100px solid;border-color:transparent transparent transparent red; }3.属性的继承 可继承的属性 …...
MFC扩展库BCGControlBar Pro v35.0新版亮点:重新设计的工具栏编辑器等
BCGControlBar库拥有500多个经过全面设计、测试和充分记录的MFC扩展类。 我们的组件可以轻松地集成到您的应用程序中,并为您节省数百个开发和调试时间。 BCGControlBar专业版 v35.0已全新发布了,这个版本改进类Visual Studio 2022的视觉主题、增强对多个…...

python调用SDK的问题
问题:Could not find module MvCameraControl.dll 原因:识别环境变量runtime异常 解决:指定具体绝对地址即可。MvCameraControl.dll的位置C:\Program Files (x86)\Common Files\MVS\Runtime\Win64_x64 MvCamCtrldll WinDLL("MvCamer…...
html入门综合练习
综合练习 通过实际项目练习可以更好地理解和掌握HTML、CSS和JavaScript。以下是几个综合练习项目的建议: 项目1:个人简历网页 创建一个包含以下内容的个人简历网页: 个人简介(姓名、照片、联系方式)教育背景工作经…...

函数模板的具体化
函数模板优点是通用性,可以解决某个方面的普遍性问题,但是这个世界上的事情不是绝对的,有普遍的,就有绝对的。举个栗子: #include <iostream> using namespace std; template <typename T> void Swap(T &…...

【Linux 内存管理】
文章目录 1. 为什么要有虚拟内存呢?🔍 1. 为什么要有虚拟内存呢?🔍...

AJAX 数据库
AJAX 数据库 1. 引言 AJAX(Asynchronous JavaScript and XML)是一种流行的网络开发技术,它允许网页在不重新加载整个页面的情况下与服务器交换数据和更新部分网页内容。AJAX技术与数据库的结合,为现代网络应用提供了更加丰富和动态的用户体验。本文将探讨AJAX如何与数据库…...

力扣719.找出第K小的数对距离
力扣719.找出第K小的数对距离 二分答案 朴素版 双指针遍历数组 超过界限break auto check [&](int mid) -> bool{int res0;for(int i0;i<n-1;i)for(int ji1;j<n;j){if(nums[j] - nums[i] > mid) break;elseif(res > k) return true;}return false;};优…...

富格林:掌握可信出金交易策略
富格林认为,黄金市场是起起落落,似乎机遇无处不在,但很少有人能真正抓住机遇。黄金可以做多也可以做空,做空主要是为了从黄金价格波动的价差中获利。只有采用正规可信的操作技巧,才能实现顺利获利出金,减少…...
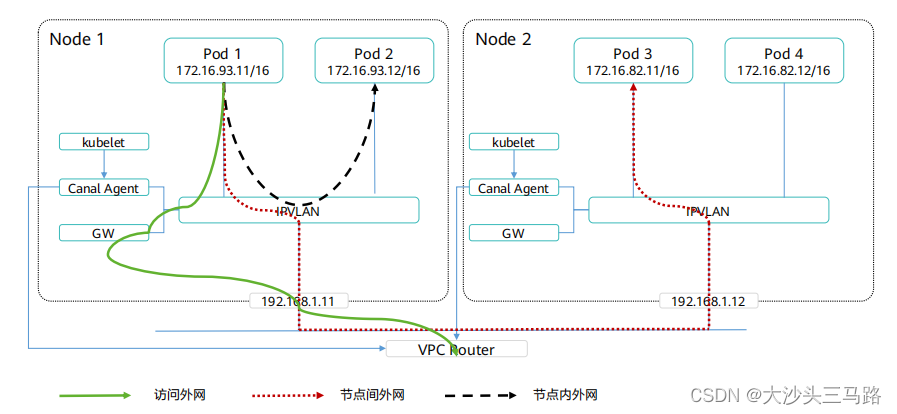
HCS-华为云Stack-容器网络
HCS-华为云Stack-容器网络 容器隧道overlay VPC网络...

【CSS in Depth2精译】1.1 层叠
CSS 本质上就是声明规则,并让这些特定的规则在各种情况下生效。一个类添加到某个元素上,则应用这个类包含的这一些样式;元素 X 是元素 Y 的一个子节点,则应用另一些样式。浏览器于是根据这些规则,判定所有样式生效的具…...

【读博日记】拓扑结构(待修正)
Topology 拓扑学 内容来源于互联网,还在甄别中——20240617 拓扑结构指把实体抽象成与其形状大小无关的点,把连接实体的线路抽象成线,再研究这些电线之间的关系。 所谓相似的拓扑结构: 例如一个圆环变成正方形、长方形、三角形…...
和setEnabled()的区别)
QT 中setVisible()和setEnabled()的区别
setVisible(bool)和setEnabled(true)在PyQt(以及其他类似的图形用户界面框架)中分别用于控制控件的可见性和可用性,它们之间的主要区别如下: setVisible(bool) 功能:这个函数用于设置QWidget控件的可见状态。参数&am…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
