【正则表达式】正则表达式语法规则
正则表达式语法规则
1.普通字符
| 字符 | 描述 |
|---|---|
[ABC] | 匹配 […] 中的所有字符 |
[^ABC] | 匹配除了 […] 中字符的所有字符 |
[A-Z] | [A-Z] 表示一个区间,匹配所有大写字母,[a-z] 表示所有小写字母 |
. | 匹配除换行符以外的任意字符 |
[\s\S] | 匹配所有。\s 是匹配所有空白符,包括换行,\S 非空白符,不包括换行 |
\w | 匹配字母、数字、下划线。等价于 [A-Za-z0-9_] |
2.非打印字符
| 字符 | 描述 |
|---|---|
\cx | 匹配由 x 指明的控制字符 |
\f | 匹配一个换页符 |
\n | 匹配一个换行符 |
\r | 匹配一个回车符 |
\s | 匹配任何空白字符,包括空格、制表符、换页符等等。等价于 [ \f\n\r\t\v] |
\S | 匹配任何非空白字符。等价于 [^ \f\n\r\t\v] |
\t | 匹配一个制表符 |
\v | 匹配一个垂直制表符 |
3.特殊字符
| 特别字符 | 描述 |
|---|---|
$ | 匹配输入字符串的结尾位置 |
() | 标记一个子表达式的开始和结束位置 |
* | 匹配前面的子表达式 000 次或多次,要匹配 * 字符,请使用 \* |
+ | 匹配前面的子表达式 111 次或多次,要匹配 + 字符,请使用 \+ |
. | 匹配除换行符 \n 之外的任何单字符。要匹配 . ,请使用 \. |
[ | 标记一个中括号表达式的开始 |
? | 匹配前面的子表达式 000 次或 111 次 |
\ | 将下一个字符标记为或特殊字符、或原义字符、或向后引用、或八进制转义符 |
^ | 匹配输入字符串的开始位置,除非在方括号表达式中使用,当该符号在方括号表达式中使用时,表示不接受该方括号表达式中的字符集合 |
{ | 标记限定符表达式的开始 |
| | 指明两项之间的一个选择 |
4.限定符
| 代码 | 说明 |
|---|---|
* | 匹配前面的子表达式 000 次或多次 |
+ | 匹配前面的子表达式 111 次或多次 |
? | 匹配前面的子表达式 000 次或 111 次 |
{n} | nnn 是一个非负整数。匹配确定的 nnn 次 |
{n,} | nnn 是一个非负整数。至少匹配 nnn 次。 |
{n,m} | mmm 和 nnn 均为非负整数,其中 n<=mn <= mn<=m。最少匹配 nnn 次且最多匹配 mmm 次。 |
5.定位符
| 代码 | 说明 |
|---|---|
^ | 匹配输入字符串开始的位置 |
$ | 匹配输入字符串结尾的位置 |
\b | 匹配一个单词边界,即字与空格间的位置 |
\B | 非单词边界匹配 |
| 代码 | 说明 |
|---|---|
?= | exp1(?=exp2):查找 exp2 前面的 exp1 |
?<= | (?<=exp2)exp1:查找 exp2 后面的 exp1 |
?! | exp1(?!exp2):查找后面不是 exp2 的 exp1 |
?<! | (?<!exp2)exp1:查找前面不是 exp2 的 exp1 |
6.修饰符
| 修饰符 | 含义 | 描述 |
|---|---|---|
i | ignore,不区分大小写 | 将匹配设置为不区分大小写,搜索时不区分大小写 |
g | global,全局匹配 | 查找所有的匹配项 |
m | multi line,多行匹配 | 使边界字符 ^ 和 $ 匹配每一行的开头和结尾,记住是多行,而不是整个字符串的开头和结尾 |
s | 特殊字符圆点 . 中包含换行符 \n | 默认情况下的圆点 . 是匹配除换行符 \n 之外的任何字符,加上 s 修饰符之后,. 中包含换行符 \n |
相关文章:

【正则表达式】正则表达式语法规则
正则表达式语法规则1.普通字符 字符描述[ABC]匹配 […] 中的所有字符[^ABC]匹配除了 […] 中字符的所有字符[A-Z][A-Z] 表示一个区间,匹配所有大写字母,[a-z] 表示所有小写字母.匹配除换行符以外的任意字符[\s\S]匹配所有。\s 是匹配所有空白符…...
1636_isatty函数的功能
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 前面刚刚看完了一个函数和三个文件指针,一行代码懂了半行。但是继续分析我之前看到的代码还是遇到了困难,因为之前自己对于UNIX的一些基础知…...
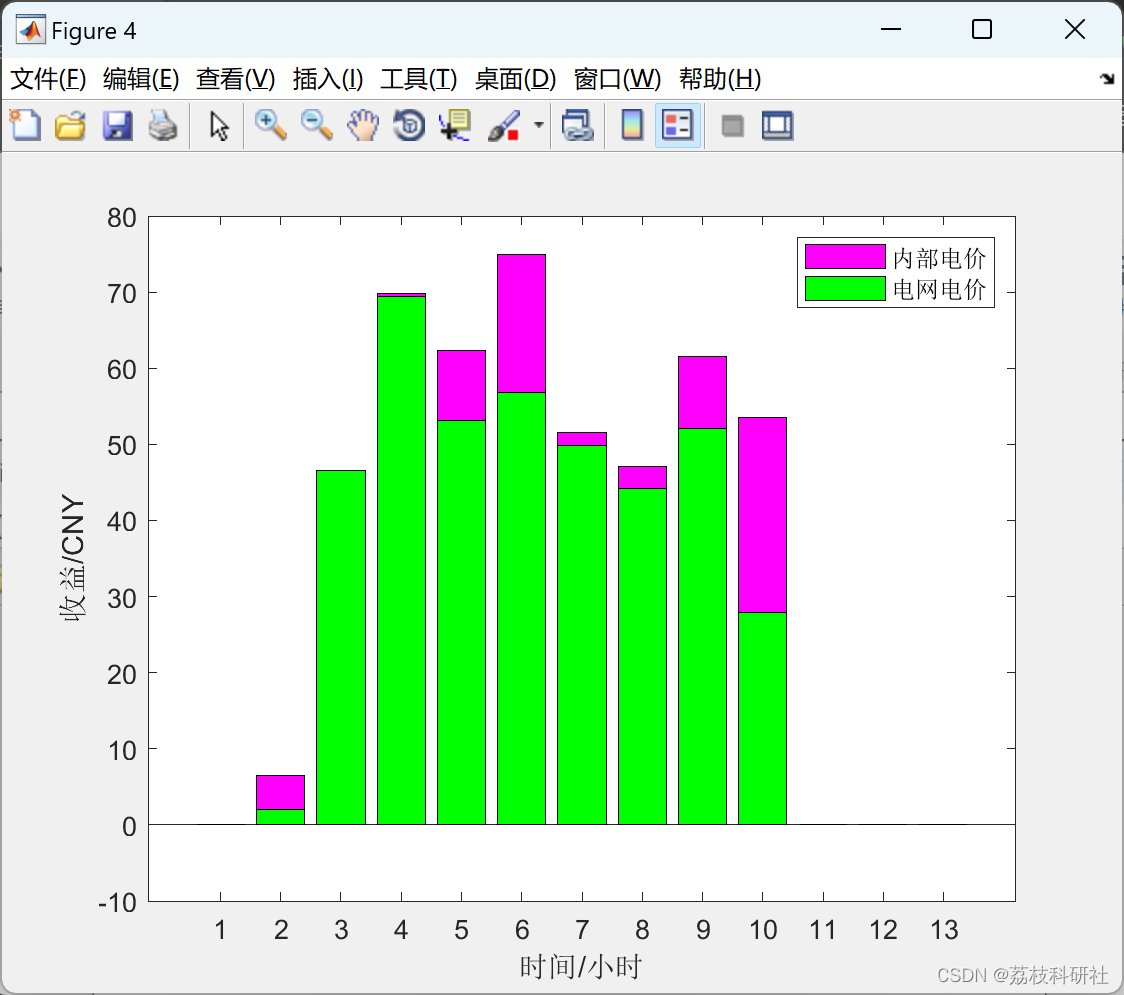
基于Stackelberg博弈的光伏用户群优化定价模型(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

EXCEL职业版本(3)
Excel职业版本(3) 公式与函数 运算符 算数运算符 关系运算符 地址的引用 相对引用:你变它就变,如影随形 A2:A5 绝对引用:以不变应万变 $A$2 混合引用:识时务者为俊杰,根据时…...

查找Pycharm跑代码下载模型存放位置以及有关模型下载小技巧(model_name_or_path参数)
目录一、前言二、发现问题三、删除这些模型方法一:直接删除注意方法二:代码删除一、前言 当服务器连不上,只能在本地跑代码时需要使用***预训练语言模型进行处理 免不了需要把模型下载到本地 时间一长就会发现C盘容量不够 二、发现问题 正…...

JS学习笔记day04
今日内容 零、 复习昨日 一、事件 二、DOM操作 三、案例 零、 复习昨日 js 脚本语言,弱类型 引入方案: 3种 js的内容: 语法dombom 语法 变量 var 数据类型 引用类型 - 对象,JSON {key:value,key:value} 数组 var arr new Array();var arr [1,2];下标取值赋值pop() s…...

异步控制流程 遍历篇
文章目录基础方法onlyOnce 只执行一次,第二次报错once 只执行一次,第二次无效iteratorSymbol 判断是否具有迭代器并返回迭代器arrayEach 普通数组遍历baseEach 对象类型遍历symbolEach 具有迭代器类型遍历异步遍历each异步控制流程的目的: 对…...
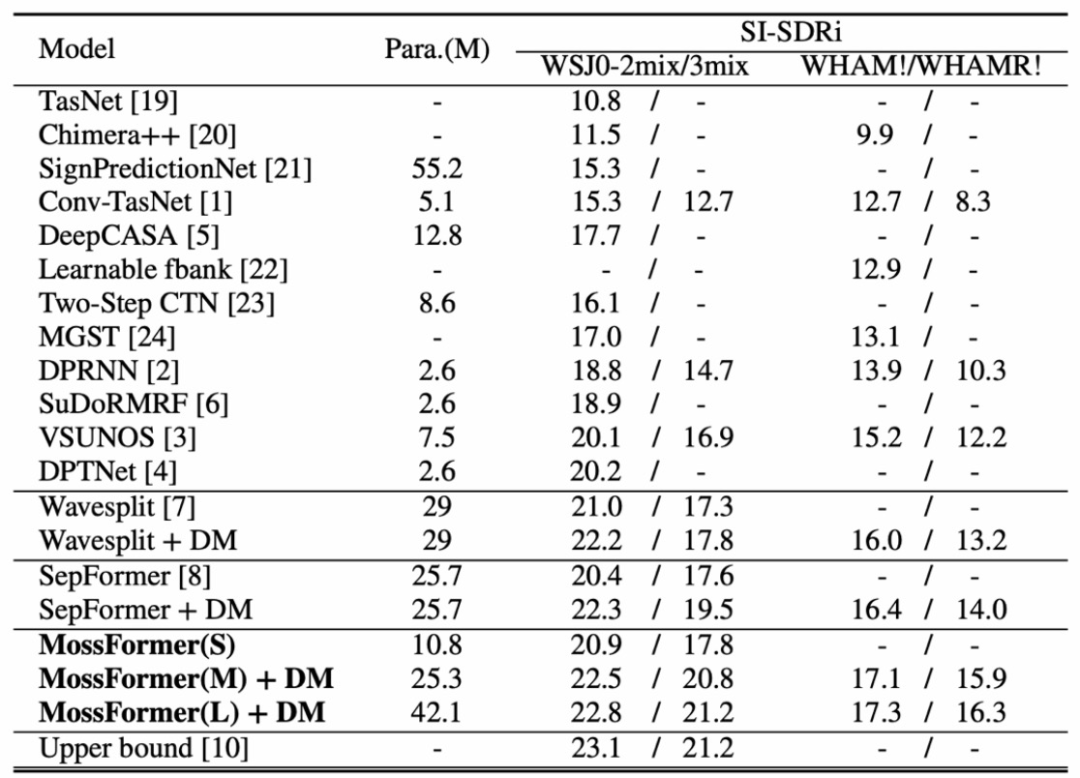
ICASSP 2023论文模型开源|语音分离Mossformer
人类能在复杂的多人说话环境中轻易地分离干扰声音,选择性聆听感兴趣的主讲人说话。但这对机器却不容易,如何构建一个能够媲美人类听觉系统的自动化系统颇具挑战性。 本文将详细解读ICASSP2023本届会议收录的单通道语音分离模型Mossformer论文࿰…...

vs2019 更改工程项目名称
本地 解决方案所在的位置为:D:\Projcet 解决方案名称:hello.sln 位置:D:\Projcet\hello.sln 工程项目名称:test 位置:D:\Projcet\test (文件夹中包含头文件,源文件) 工程包含的文件: fun.h …...
FusionCompute安装和配置步骤
1. 先去华为官网下载FusionCompute的镜像 下载地址:https://support.huawei.com/enterprise/zh/distributed-storage/fusioncompute-pid-8576912/software/251713663?idAbsPathfixnode01%7C22658044%7C7919788%7C9856606%7C21462752%7C8576912 下载后放在D盘中&am…...

makefile 参数和基本使用
make 常用选项make[-f file] [options] [target]make 默认在当前目录中查找GUNmakefile、makefile 及 Makefile 文件作为make的输入文件-f 指定文件作为输入文件-v 显示版本号-n 只输出命令不执行, 一般作为测试-s 执行命令不显示命令,-w 显示执行前和执…...

golang 占位符还傻傻分不清?
xdm ,写 C/C 语言的时候有格式控制符,例如 %s , %d , %c , %p 等等 在写 golang 的时候,也是有对应的格式控制符,也叫做占位符,写这个占位符,需要有对应的数据与之对应,不能瞎搞 基本常见常用…...

manacher算法详解
例题 求一个字符串的最长回文子串的长度 O(N2)O(N^2)O(N2)的解法很容易想,就是从每个字符位置向左右同时拓展,然后检查当前是不是回文,更新长度,可以简单写一下代码 int solve(string &ss){int ans 0;int n ss.length();s…...

要做一个关于DDD的内部技术分享,记录下用到的资源,学习笔记(未完)
最后更新于2023年3月10日 14:28:08 问题建模》软件分层》具体结构,是层层递进的关系。有了问题建模,才能进行具体的软件分层的讨论,再有了分层,才能讨论在domain里面应该怎么实现具体结构。 1、问题建模:Domain、Mod…...

KDZD互感器二次负载测试仪
一、概述 电能计量综合误差过大是电能计量中普遍存在的一个关键问题。电压互感器二次回路压降引起的计量误差往往是影响电能计量综合误差的因素。所谓电压互感器二次压降引起的误差,就是指电压互感器二次端子和负载端子之间电压的幅值差相对于二次实际电压的百分数…...
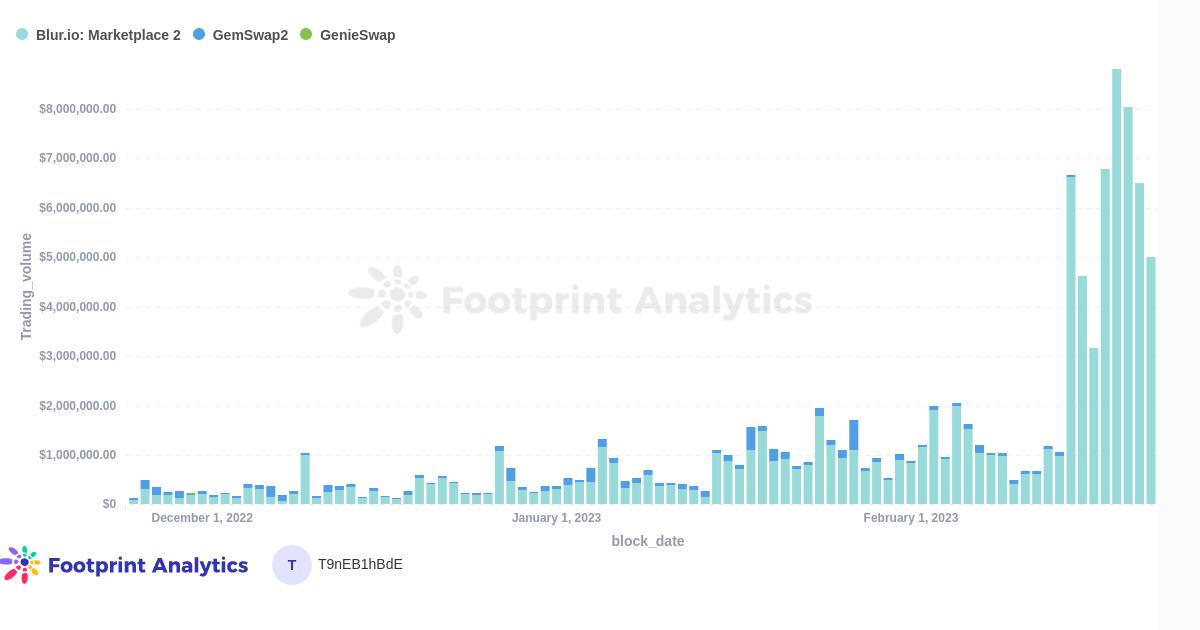
在空投之后,Blur能否颠覆OpenSea的主导地位?
Mar. 2023, Daniel数据源: NFT Aggregators Overview & Aggregator Statistics Overview & Blur Airdrop一年前,通过聚合器进行的NFT交易量开始像滚雪球一样增长,有时甚至超过了直接通过市场平台的交易量。虽然聚合器的使用量从10月到…...
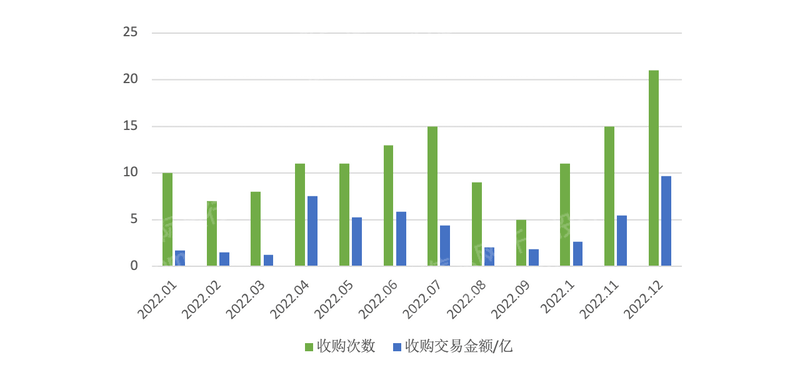
2023年新三板产品及服务研究报告
第一章 概述 全国中小企业股份转让系统(英语:National Equities Exchange and Quotations,缩写NEEQ),简称股转系统,是第三家全国性证券交易场所,因挂牌企业均为高科技企业而不同于原转让系统内…...
张力控制之开环模式
张力控制的相关知识也可以参看专栏的其它文章,链接如下: 张力闭环控制之传感器篇(精密调节气阀应用)_RXXW_Dor的博客-CSDN博客跳舞轮对应张力调节范围,我们可以通过改变气缸的气压方式间接改变,张力跳舞轮在收放卷闭环控制上的详细应用,可以参看下面的文章链接,这里我…...

python的django框架从入门到熟练【保姆式教学】第二篇
在上一篇博客中,我们介绍了Django的基础知识,并创建了一个简单的Web应用程序。在本篇教程中,我们将深入探讨Django的模型层(Model),它是Django应用程序的核心组件之一。 模型层 Django的模型层是一个对象…...
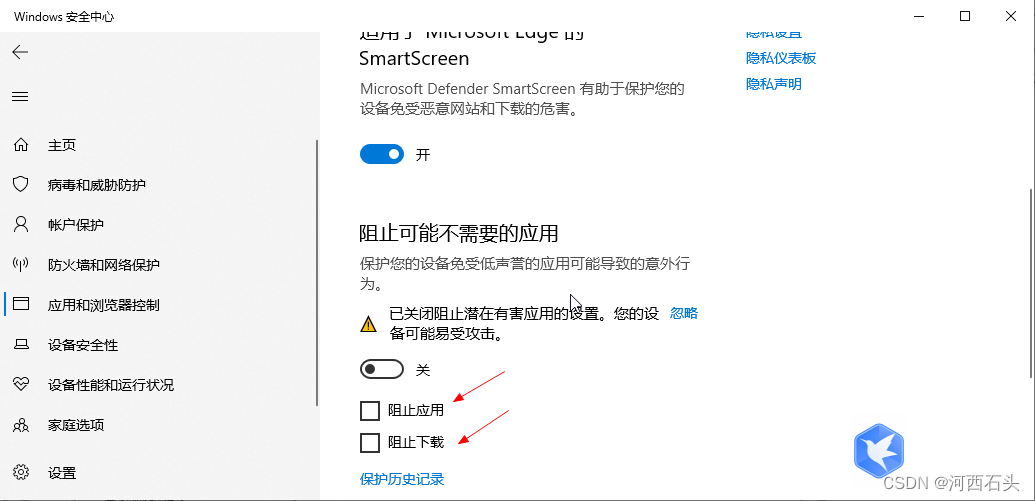
解决win10的过度保护导致文件下载不了程序不能打开运行
win7看来大概是要离我们远去了,虽然我们还能看见她的背影,但大势所趋,我们也只能慢慢的接受win10进入到我们的日常生活。但win10很多时候过度的保护却给我们带来了不便。这里列举两个最常见的问题,当然我这里也给出了解决方案。 文…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
