高等数学——多元函数微分学
文章目录
- 多元函数微分学
- 多元函数的极限
- 多元函数的连续性
- 偏导数
- 定义
- 高阶偏导数
- 全微分
- 定义
- 全微分存在的必要条件
- 全微分存在的充分条件
- 多元函数的微分法
- 复合函数微分法
- 隐函数微分法
- 多元函数的极值与最值
- 无约束极值
- 条件极值及拉格朗日乘数法
- 最大值最小值
- 二重积分
- 概念
- 性质
- 计算
- 利用直角坐标计算
- 利用极坐标计算
- 利用函数的奇偶性计算
- 利用变量的轮换对称性计算
多元函数微分学
设DDD是平面上的一个点集,若对每个点P(x,y)∈DP(x,y)∈DP(x,y)∈D,变量zzz按照某一对应法则fff有一个确定的值与之对应,则称zzz为x,yx,yx,y的二元函数,记为z=f(x,y)z=f(x,y)z=f(x,y)。其中点集DDD称为该函数的定义域,x,yx,yx,y称为自变量,zzz称为因变量,函数f(x,y)f(x,y)f(x,y)的全体所构成的集合称为函数fff的值域,记为f(D)f(D)f(D)。通常情况下,二元函数在几何上表示一张空间曲面。
多元函数的极限
设函数f(x,y)f(x,y)f(x,y)在区域DDD上有定义,点P0(x0,y0)∈DP_0(x_0,y_0)∈DP0(x0,y0)∈D或为DDD的边界点,如果∀ε>0\forall\varepsilon>0∀ε>0,存在δ>0\delta>0δ>0,当P(x,y)∈DP(x,y)∈DP(x,y)∈D,且0<(x−x0)2+(y−y0)2<δ0<\sqrt{(x-x_0)^2+(y-y_0)^2}<\delta0<(x−x0)2+(y−y0)2<δ时,都有∣f(x)−A∣<ε|f(x)-A|<\varepsilon∣f(x)−A∣<ε成立,则称常数AAA为函数f(x,y)f(x,y)f(x,y)当(x,y)→(x0,y0)(x,y)\to(x_0,y_0)(x,y)→(x0,y0)时的极限,记为lim(x,y)→(x0,y0)f(x,y)=A\lim\limits_{(x,y)\to(x_0,y_0)}f(x,y)=A(x,y)→(x0,y0)limf(x,y)=A或limx→x0y→y0f(x,y)=A\lim\limits_{x\to x_0 y\to y_0}f(x,y)=Ax→x0y→y0limf(x,y)=A或limP→P0f(P)=A\lim\limits_{P\to P_0}f(P)=AP→P0limf(P)=A。一元函数的以下性质对多元函数仍然适用:
- 局部有界性
- 保号性
- 有理运算
- 极限与无穷小的关系
- 夹逼原理
多元函数的连续性
设函数f(x,y)f(x,y)f(x,y)在区域DDD上有定义,点P0(x0,y0)∈DP_0(x_0,y_0)∈DP0(x0,y0)∈D,如果lim(x,y)→(x0,y0)f(x,y)=f(x0,y0)\lim\limits_{(x,y)\to(x_0,y_0)}f(x,y)=f(x_0,y_0)(x,y)→(x0,y0)limf(x,y)=f(x0,y0)成立,则称函数f(x,y)f(x,y)f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)连续,如果f(x,y)f(x,y)f(x,y)在区域DDD上的每个点(x,y)(x,y)(x,y)处都连续,则称函数f(x,y)f(x,y)f(x,y)在区域DDD上连续。
- 性质一:多元函数的和、差、积、商(分母不为零)仍为连续函数。
- 性质二:多元连续函数的复合函数也是连续函数。
- 性质三:多元初等函数在其定义区域内连续。
- 性质四(最大最小值定理):有界闭区域DDD上的连续函数在区域DDD上必能取得最大值和最小值。
- 性质五(介值定理):有界闭区域DDD上的连续函数在区域DDD上必能取得介于最大值和最小值之间的任何值。
偏导数
定义
设z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)的某一邻域内有定义,如果limΔx→0f(x0+Δx,y0)−f(x0,y0)Δx\lim\limits_{\Delta x\to0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}Δx→0limΔxf(x0+Δx,y0)−f(x0,y0)存在,则称这个极限值为函数z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)处对xxx的偏导数,记为∂z∂x∣x=x0y=x0\frac{\partial z}{\partial x}|_{x=x_0 y=x_0}∂x∂z∣x=x0y=x0或∂f∂x∣x=x0y=x0\frac{\partial f}{\partial x}|_{x=x_0 y=x_0}∂x∂f∣x=x0y=x0或fx′(x0,y0)f'_x(x_0,y_0)fx′(x0,y0)。类似的,如果limΔy→0f(x0,y0+Δy)−f(x0,y0)Δy\lim\limits_{\Delta y\to0}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}Δy→0limΔyf(x0,y0+Δy)−f(x0,y0)存在,则称这个极限值为函数z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)处对yyy的偏导数,记为∂z∂y∣x=x0y=x0\frac{\partial z}{\partial y}|_{x=x_0 y=x_0}∂y∂z∣x=x0y=x0或∂f∂y∣x=x0y=x0\frac{\partial f}{\partial y}|_{x=x_0 y=x_0}∂y∂f∣x=x0y=x0或fy′(x0,y0)f'_y(x_0,y_0)fy′(x0,y0)。
高阶偏导数
如果f(x,y)f(x,y)f(x,y)在区域DDD内的偏导数∂z∂x,∂z∂y\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}∂x∂z,∂y∂z仍然存在偏导数,则称之为函数f(x,y)f(x,y)f(x,y)的二阶偏导数,常记为∂∂x∂z∂x=∂2z∂x2\frac{\partial}{\partial x}{\frac{\partial z}{\partial x}}=\frac{\partial^2z}{\partial x^2}∂x∂∂x∂z=∂x2∂2z或fxx′′f''_{xx}fxx′′,∂∂y∂z∂x=∂2z∂x∂y\frac{\partial}{\partial y}{\frac{\partial z}{\partial x}}=\frac{\partial^2z}{\partial x \partial y}∂y∂∂x∂z=∂x∂y∂2z或fxy′′f''_{xy}fxy′′,∂∂x∂z∂y=∂2z∂y∂x\frac{\partial}{\partial x}{\frac{\partial z}{\partial y}}=\frac{\partial^2z}{\partial y \partial x}∂x∂∂y∂z=∂y∂x∂2z或fyx′′f''_{yx}fyx′′,∂∂y∂z∂y=∂2z∂y2\frac{\partial}{\partial y}{\frac{\partial z}{\partial y}}=\frac{\partial^2z}{ \partial y^2}∂y∂∂y∂z=∂y2∂2z或fyy′′f''_{yy}fyy′′。常称∂2z∂x∂y,∂2z∂y∂x\frac{\partial^2z}{\partial x \partial y},\frac{\partial^2z}{\partial y \partial x}∂x∂y∂2z,∂y∂x∂2z为混合偏导数。如果函数f(x,y)f(x,y)f(x,y)的两个二阶混合偏导数∂2z∂x∂y,∂2z∂y∂x\frac{\partial^2z}{\partial x \partial y},\frac{\partial^2z}{\partial y \partial x}∂x∂y∂2z,∂y∂x∂2z在区域DDD内连续,则在该区域内这两个混合偏导数一定相等。
全微分
定义
如果函数f(x,y)f(x,y)f(x,y)在(x0,y0)(x_0,y_0)(x0,y0)处的全增量Δx=f(x0+Δx,y0+Δy)−f(x0,y0)\Delta x=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)Δx=f(x0+Δx,y0+Δy)−f(x0,y0)可表示为δx=AΔx+BΔy+o(ρ)\delta x=A\Delta x+B\Delta y+o(\rho)δx=AΔx+BΔy+o(ρ),其中A,BA,BA,B与Δx,Δy\Delta x,\Delta yΔx,Δy无关,ρ=(Δx)2+(Δy)2\rho=\sqrt{(\Delta x)^2+(\Delta y)^2}ρ=(Δx)2+(Δy)2,则称函数z=f(x,y)z=f(x,y)z=f(x,y)在点(x0,y0)(x_0,y_0)(x0,y0)处可微,而AΔx+BΔyA\Delta x+B\Delta yAΔx+BΔy称为函数f(x,y)f(x,y)f(x,y)在点(x0,y0)(x_0,y_0)(x0,y0)处的全微分,记为dz=AΔx+BΔydz=A\Delta x+B\Delta ydz=AΔx+BΔy。如果f(x,y)f(x,y)f(x,y)在区域DDD内的每一点(x,y)(x,y)(x,y)都可微分,则称f(x,y)f(x,y)f(x,y)在DDD内可微。
全微分存在的必要条件
如果函数f(x,y)f(x,y)f(x,y)在(x0,y0)(x_0,y_0)(x0,y0)处可微,则该函数在点(x,y)(x,y)(x,y)处的偏导数∂z∂x,∂z∂y\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}∂x∂z,∂y∂z必定存在,且dz=∂z∂xdx+∂z∂ydydz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dydz=∂x∂zdx+∂y∂zdy。用定义判断函数f(x,y)f(x,y)f(x,y)在(x0,y0)(x_0,y_0)(x0,y0)处的可微性分为以下两步:
- fx′(x0,y0)f'_x(x_0,y_0)fx′(x0,y0)和fy′(x0,y0)f'_y(x_0,y_0)fy′(x0,y0)是否存在。
- limΔx→0Δy→0[f(x0+Δx,y0+Δy)−f(x0,y0)]−[fx′(x0,y0)Δx+fy′(x0,y0)Δy](Δx)2+(Δy)2\lim\limits_{\Delta x\to 0 \Delta y \to 0}\frac{[f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)]-[f'_x(x_0,y_0)\Delta x+f'_y(x_0,y_0)\Delta y]}{\sqrt{(\Delta x)^2+(\Delta y)^2}}Δx→0Δy→0lim(Δx)2+(Δy)2[f(x0+Δx,y0+Δy)−f(x0,y0)]−[fx′(x0,y0)Δx+fy′(x0,y0)Δy]是否等于零。
全微分存在的充分条件
如果函数f(x,y)f(x,y)f(x,y)的偏导数∂z∂x,∂z∂y\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}∂x∂z,∂y∂z在点(x0,y0)(x_0,y_0)(x0,y0) 处连续,则函数f(x,y)f(x,y)f(x,y)在点(x0,y0)(x_0,y_0)(x0,y0) 处可微。
多元函数的微分法
复合函数微分法
- 定义:设函数u=u(x,y),v=v(x,y)u=u(x,y),v=v(x,y)u=u(x,y),v=v(x,y)在点(x,y)(x,y)(x,y)处有对xxx及对yyy的偏导数,函数z=f(u,v)z=f(u,v)z=f(u,v)在对应点(u,v)(u,v)(u,v)处有连续偏导数,则复合函数z=f[u(x,y),v(x,y)]z=f[u(x,y),v(x,y)]z=f[u(x,y),v(x,y)]在点(x,y)处的两个偏导数存在,且有∂z∂x=∂z∂u∂u∂x+∂z∂v∂v∂x,∂z∂y=∂z∂u∂u∂y+∂z∂v∂v∂y\frac{\partial z}{\partial x}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial x}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial x},\frac{\partial z}{\partial y}=\frac{\partial z}{\partial u}\frac{\partial u}{\partial y}+\frac{\partial z}{\partial v}\frac{\partial v}{\partial y}∂x∂z=∂u∂z∂x∂u+∂v∂z∂x∂v,∂y∂z=∂u∂z∂y∂u+∂v∂z∂y∂v。
- 全微分形式的不变性:设函数z=f(u,v),u=u(x,y)z=f(u,v),u=u(x,y)z=f(u,v),u=u(x,y),及v=v(x,y)v=v(x,y)v=v(x,y)都有连续的一阶偏导数,则复合函数z=f[u(x,y),v(x,y)]z=f[u(x,y),v(x,y)]z=f[u(x,y),v(x,y)]的全微分dx=∂z∂xdx+∂z∂ydy+∂z∂udu+∂z∂vdvdx=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy+\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dvdx=∂x∂zdx+∂y∂zdy+∂u∂zdu+∂v∂zdv,即:不论把函数zzz看左子按量x,yx,yx,y的函数,还是看作中间变量u,vu,vu,v的函数,函数zzz的全微分形式都是一样的。
隐函数微分法
- 由方程F(x,y)=0F(x,y)=0F(x,y)=0确定的隐函数y=y(x)y=y(x)y=y(x):若函数F(x,y)F(x,y)F(x,y)在点P(x0,y0)P(x_0,y_0)P(x0,y0) 的某一邻域内有连续偏导数,且F(x0,y0)=0,Fy′(x0,y0)≠0F(x_0,y_0)=0,F'_y(x_0,y_0)≠0F(x0,y0)=0,Fy′(x0,y0)=0,则方程F(x,y)=0F(x,y)=0F(x,y)=0在点(x0,y0)(x_0,y_0)(x0,y0)的某邻域可唯一确定一个有连续导数的函数y=f(x)y=f(x)y=f(x),并有y′=Fx′Fy′y'=\frac{F'_x}{F'_y}y′=Fy′Fx′。
- 由方程F(x,y,z)=0F(x,y,z)=0F(x,y,z)=0确定的隐函数z=z(x,y)z=z(x,y)z=z(x,y):若函数F(x,y,z)F(x,y,z)F(x,y,z)在点P(x0,y0,z0)P(x_0,y_0,z_0)P(x0,y0,z0)的某一邻域内有连续偏导数,且F(x0,y0,z0)=0,Fy′(x0,y0,z0)≠0F(x_0,y_0,z_0)=0,F'_y(x_0,y_0,z_0)≠0F(x0,y0,z0)=0,Fy′(x0,y0,z0)=0,则方程F(x,y,z)=0F(x,y,z)=0F(x,y,z)=0在点(x0,y0,z0)(x_0,y_0,z_0)(x0,y0,z0)的某邻域可唯一确定一个有连续导数的函数z=f(x,y)z=f(x,y)z=f(x,y),并有∂z∂x=Fx′Fz′,∂z∂y=Fy′Fz′\frac{\partial z}{\partial x}=\frac{F'_x}{F'_z},\frac{\partial z}{\partial y}=\frac{F'_y}{F'_z}∂x∂z=Fz′Fx′,∂y∂z=Fz′Fy′。
多元函数的极值与最值
无约束极值
设函数z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)的某邻域内有定义,若对该邻域内任意的点P(x,y)P(x,y)P(x,y)均有f(x,y)≤f(x0,y0)f(x,y)≤f(x_0,y_0)f(x,y)≤f(x0,y0),则称(x0,y0)(x_0,y_0)(x0,y0)为f(x,y)f(x,y)f(x,y)的极大值点,称f(x0,y0)f(x_0,y_0)f(x0,y0)为f(x,y)f(x,y)f(x,y)的极大值。极大值和极小值点统称为极值点,极大值极小值统称为极值。
- 极值的i要条件:设函数z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)存在偏导数,且(x0,y0)(x_0,y_0)(x0,y0)为f(x,y)f(x,y)f(x,y)的极值点,则fx′(x0,y0)=0,fy′(x0,y0)=0f'_x(x_0,y_0)=0,f'_y(x_0,y_0)=0fx′(x0,y0)=0,fy′(x0,y0)=0。
- 极值的充分条件:设函数z=f(x,y)z=f(x,y)z=f(x,y)在点P0(x0,y0)P_0(x_0,y_0)P0(x0,y0)的某邻域内有二阶连续偏导数,又fx′(x0,y0)=0,fy′(x0,y0)f'_x(x_0,y_0)=0,f'_y(x_0,y_0)fx′(x0,y0)=0,fy′(x0,y0),记A=fxx′′(x0,y0),B=fxy′′(x0,y0),C=fyy′′(x0,y0)A=f''_{xx}(x_0,y_0),B=f''_{xy}(x_0,y_0),C=f''_{yy}(x_0,y_0)A=fxx′′(x0,y0),B=fxy′′(x0,y0),C=fyy′′(x0,y0)则有以下结论:
-
- 若AC−B2>0AC-B^2>0AC−B2>0,则(x0,y))(x_0,y_))(x0,y))为f(x,y)f(x,y)f(x,y)的极值点。若A<0A<0A<0,则(x),y))(x_),y_))(x),y))为f(x,y)f(x,y)f(x,y)的极大值点;若A>0A>0A>0,则(x),y))(x_),y_))(x),y))为f(x,y)f(x,y)f(x,y)的极小值点。
-
- 若AC−B2<0AC-B^2<0AC−B2<0,则(x0,y))(x_0,y_))(x0,y))不为f(x,y)f(x,y)f(x,y)的极值点。
-
- 若AC−B2=0AC-B^2=0AC−B2=0,则(x0,y))(x_0,y_))(x0,y))可能为f(x,y)f(x,y)f(x,y)的极值点,也可能不为f(x,y)f(x,y)f(x,y)的极值点(此时一般用定义判断)。
求具有二阶连续偏导数的二元函数z=f(x,y)z=f(x,y)z=f(x,y)极值的一般步骤为:
- 求出f(x,y)f(x,y)f(x,y)的驻点P1...PkP_1...P_kP1...Pk。
- 利用极值的充分条件判定驻点PiP_iPi是否是驻点。
条件极值及拉格朗日乘数法
求z=f(x,y)z=f(x,y)z=f(x,y)在条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0下的条件极值的一般方法为:
- 构造拉格朗日函数F(x,y,λ)=f(x,y)+λp(x,y)F(x,y,\lambda)=f(x,y)+\lambda p(x,y)F(x,y,λ)=f(x,y)+λp(x,y)
- 将F(x,y,λ)F(x,y,\lambda)F(x,y,λ)分别对x,y,zx,y,zx,y,z求偏导数,构造方程组{fx′(x,y)+λφx′(x,y)=0,fy′(x,y)+λφy′(x,y)=0,φ(x,y)=0\begin{cases}f'_x(x,y)+\lambda\varphi'_x(x,y)=0,\\f'_y(x,y)+\lambda\varphi'_y(x,y)=0,\\\varphi(x,y)=0\end{cases}⎩⎨⎧fx′(x,y)+λφx′(x,y)=0,fy′(x,y)+λφy′(x,y)=0,φ(x,y)=0。
解出x,y,λx,y,\lambdax,y,λ,则其中(x,y)(x,y)(x,y)就是函数f(x,y)f(x,y)f(x,y)在条件φ(x,y)=0\varphi(x,y)=0φ(x,y)=0下的可能极值点。
最大值最小值
求连续函数f(x,y)f(x,y)f(x,y)在有界闭区域DDD上的最大值:
- 求f(x,y)f(x,y)f(x,y)在点DDD内部可能的极值点。
- 求f(x,y)f(x,y)f(x,y)在点DDD的边界上的最大最小值。
二重积分
概念
- 定义:设函数z=f(x,y)z=f(x,y)z=f(x,y)在有界区域DDD上有定义,将区域DDD任意分成nnn个小区域Δσ1,Δσ2,...,Δσn\Delta\sigma_1,\Delta\sigma_2,...,\Delta\sigma_nΔσ1,Δσ2,...,Δσn,其中Δσi\Delta\sigma_iΔσi代表第iii个小区域,也表示它的面积,在每个Δσi\Delta\sigma_iΔσi上任取一点(ξi,ηi)(\xi_i,\eta_i)(ξi,ηi),做乘积f(ξi,ηi)Δσif(\xi_i,\eta_i)\Delta\sigma_if(ξi,ηi)Δσi,并求和∑i=1nf(ξi,ηi)Δσi\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i∑i=1nf(ξi,ηi)Δσi,记λ\lambdaλ为nnn个小区域Δσ1,Δσ2,...,Δσn\Delta\sigma_1,\Delta\sigma_2,...,\Delta\sigma_nΔσ1,Δσ2,...,Δσn中最大直径,如果∑i=1nf(ξi,ηi)Δσi\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i∑i=1nf(ξi,ηi)Δσi存在,则称f(x,y)f(x,y)f(x,y)在区域DDD上的二重积分,记为∬Df(x,y)dσ=limλ→0∑i=1nf(ξi,ηi)Δσi\iint_Df(x,y)d\sigma=\lim\limits_{\lambda\to 0}\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i∬Df(x,y)dσ=λ→0lim∑i=1nf(ξi,ηi)Δσi。
- 几何意义:二重积分∬Df(x,y)dσ\iint_Df(x,y)d\sigma∬Df(x,y)dσ是一个数,当f(x,y)≥0f(x,y)≥0f(x,y)≥0时,其值等于以区域DDD为底,以曲面z=f(x,y)z=f(x,y)z=f(x,y)为曲顶柱体的体积,当f(x,y)≤0f(x,y)≤0f(x,y)≤0时,二重积分的值为负数,其绝对值等于上述曲顶柱体的体积。
性质
- 不等式性质:若在DDD上f(x,y)≤g(x,y)f(x,y)≤g(x,y)f(x,y)≤g(x,y),则∬Df(x,y)dσ≤∬Dg(x,y)dσ\iint_Df(x,y)d\sigma≤\iint_Dg(x,y)d\sigma∬Df(x,y)dσ≤∬Dg(x,y)dσ;若在DDD上m≤f(x,y)≤Mm≤f(x,y)≤Mm≤f(x,y)≤M,则mσ≤∬Df(x,y)dσ≤Mσm\sigma≤\iint_Df(x,y)d\sigma≤M\sigmamσ≤∬Df(x,y)dσ≤Mσ(其中σ\sigmaσ为区域DDD的面积);∣∬Df(x,y)dσ∣≤∬D∣f(x,y)∣dσ|\iint_Df(x,y)d\sigma|≤\iint_D|f(x,y)|d\sigma∣∬Df(x,y)dσ∣≤∬D∣f(x,y)∣dσ。
- 中值定理:设函数f(x,y)f(x,y)f(x,y)在闭区域DDD上连续,σ\sigmaσ为区域DDD的面积,则在DDD上至少存在一点(ξ,η)(\xi,\eta)(ξ,η),使得∬Df(x,y)dσ=f(ξ,η)σ\iint_Df(x,y)d\sigma=f(\xi,\eta)\sigma∬Df(x,y)dσ=f(ξ,η)σ。
计算
利用直角坐标计算
- 先yyy后xxx,积分区域DDD可以用a≤x≤ba≤x≤ba≤x≤b,φ1(x)≤y≤φ2(x)\varphi_1(x)≤y≤\varphi_2(x)φ1(x)≤y≤φ2(x)表示:∬Df(x,y)dσ=∫abdx∫φ1(x)φ2(x)f(x,y)dy\iint_Df(x,y)d\sigma=\int_a^bdx\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy∬Df(x,y)dσ=∫abdx∫φ1(x)φ2(x)f(x,y)dy。
- 先xxx后yyy,积分区域DDD可以用a≤y≤ba≤y≤ba≤y≤b,φ1(y)≤x≤φ2(y)\varphi_1(y)≤x≤\varphi_2(y)φ1(y)≤x≤φ2(y)表示:∬Df(x,y)dσ=∫abdy∫φ1(y)φ2(y)f(x,y)dx\iint_Df(x,y)d\sigma=\int_a^bdy\int_{\varphi_1(y)}^{\varphi_2(y)}f(x,y)dx∬Df(x,y)dσ=∫abdy∫φ1(y)φ2(y)f(x,y)dx。
利用极坐标计算
适合使用极坐标计算的二重积分的特征:
- 适合使用极坐标计算的被积函数:f(x2+y2)f(yx),f(xy)f(\sqrt{x^2+y^2})f(\frac{}y{x}),f(\frac{x}{y})f(x2+y2)f(yx),f(yx)。
- 适合用极坐标的积分域如:x2+y2≤R2,r2≤x2+y2≤R2,x2+y2≤2ax,x2+y2≤2byx^2+y^2≤R^2,r^2≤x^2+y^2≤R^2,x^2+y^2≤2ax,x^2+y^2≤2byx2+y2≤R2,r2≤x2+y2≤R2,x2+y2≤2ax,x2+y2≤2by。
利用函数的奇偶性计算
- 若积分区域DDD关于yyy轴对称,f(x,y)f(x,y)f(x,y)关于xxx轴有奇偶性,则∬Df(x,y)dσ={2∬Dx≥0f(x,y)dσ,f(x,y)关于x为偶函数0,f(x,y)关于x为奇函数\iint_Df(x,y)d\sigma=\begin{cases}2\iint_{D_x≥0}f(x,y)d\sigma,f(x,y)关于x为偶函数\\0,f(x,y)关于x为奇函数\end{cases}∬Df(x,y)dσ={2∬Dx≥0f(x,y)dσ,f(x,y)关于x为偶函数0,f(x,y)关于x为奇函数。
- 若积分区域DDD关于xxx轴对称,f(x,y)f(x,y)f(x,y)关于yyy轴有奇偶性,则∬Df(x,y)dσ={2∬Dy≥0f(x,y)dσ,f(x,y)关于y为偶函数0,f(x,y)关于y为奇函数\iint_Df(x,y)d\sigma=\begin{cases}2\iint_{D_y≥0}f(x,y)d\sigma,f(x,y)关于y为偶函数\\0,f(x,y)关于y为奇函数\end{cases}∬Df(x,y)dσ={2∬Dy≥0f(x,y)dσ,f(x,y)关于y为偶函数0,f(x,y)关于y为奇函数。
利用变量的轮换对称性计算
如果积分区域DDD具有轮换对称性,也就是关于直线y=xy=xy=x对称,即DDD的表达式中将xxx换作yyy,yyy换作xxx表达式不变,则∬Df(x,y)dσ=∬Df(y,x)dσ\iint_Df(x,y)d\sigma=\iint_Df(y,x)d\sigma∬Df(x,y)dσ=∬Df(y,x)dσ。
相关文章:

高等数学——多元函数微分学
文章目录多元函数微分学多元函数的极限多元函数的连续性偏导数定义高阶偏导数全微分定义全微分存在的必要条件全微分存在的充分条件多元函数的微分法复合函数微分法隐函数微分法多元函数的极值与最值无约束极值条件极值及拉格朗日乘数法最大值最小值二重积分概念性质计算利用直…...
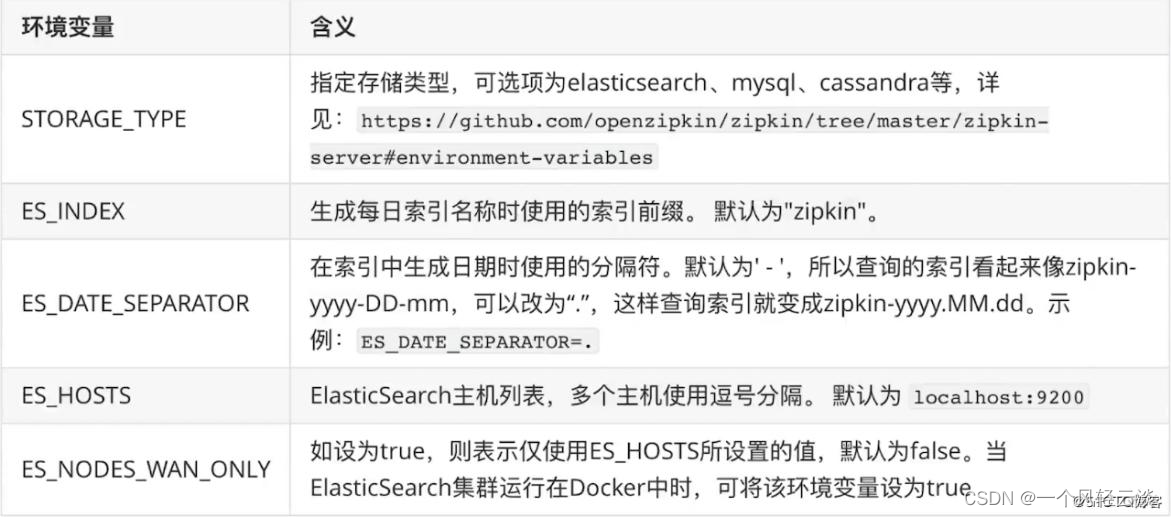
一文打通Sleuth+Zipkin 服务链路追踪
1、为什么用 微服务架构是一个分布式架构,它按业务划分服务单元,一个分布式系统往往有很多个服务单元。由于服务单元数量众多,业务的复杂性,如果出现了错误和异常,很难去定位。主要体现在,一个请求可能需要…...
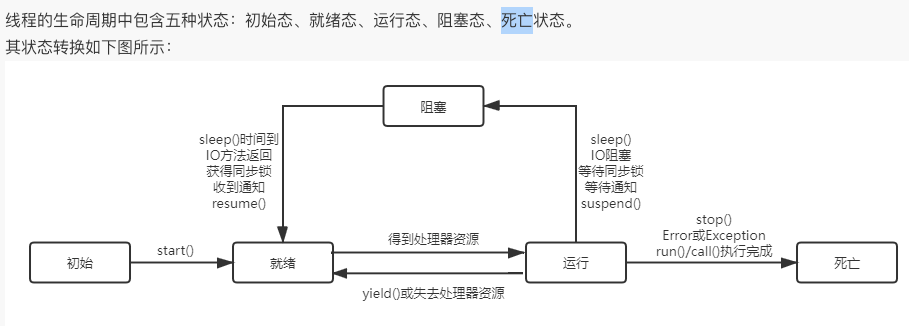
牛客刷题第一弹
1.异常处理 都是Throwable的子类: ①.Exception(异常):是程序本身可以处理的异常。 ②.Error(错误): 是程序无法处理的错误。这些错误表示故障发生于虚拟机自身、或者发生在虚拟机试图执行应用时,一般不需…...
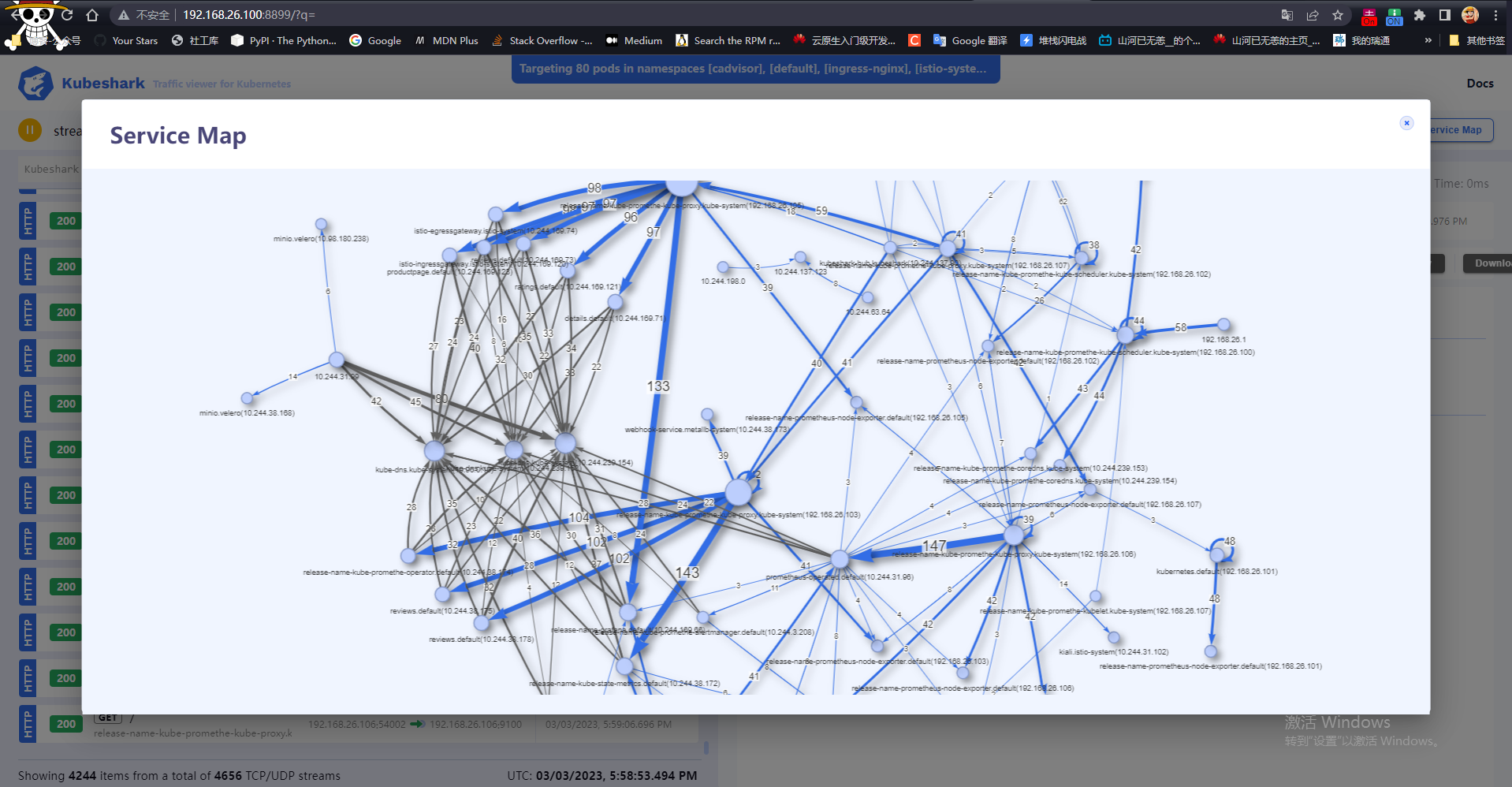
K8s:通过 Kubeshark 体验 大白鲨(Wireshark)/TCPDump 监控 Kubernetes 集群
写在前面 分享一个 k8s 集群流量查看器很轻量的一个工具,监控方便博文内容涉及: Kubeshark 简单介绍Windows、Linux 下载运行监控DemoKubeshark 特性功能介绍 理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。…...
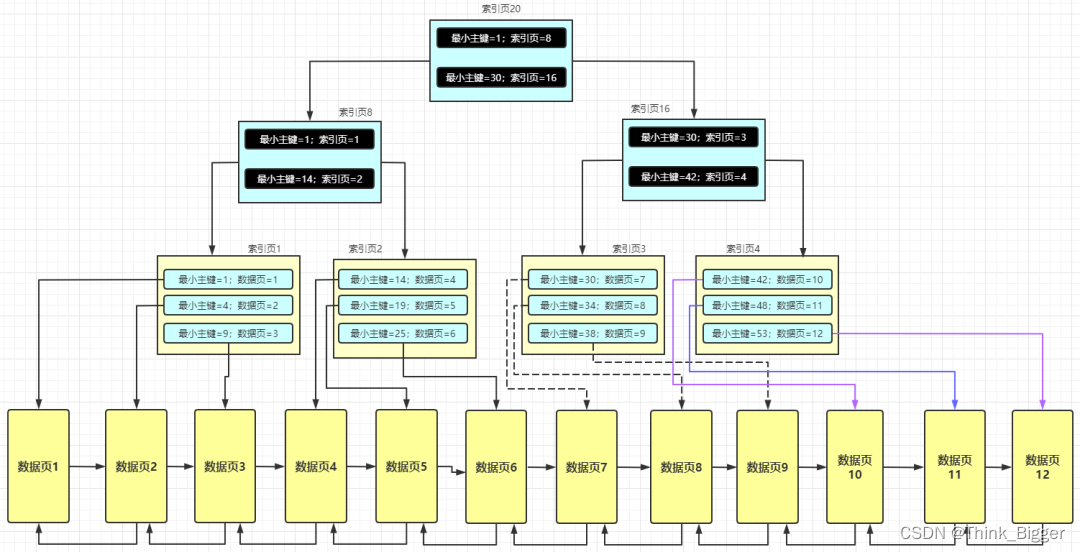
MySQL查询索引原则
文章目录 等值匹配原则最左前缀匹配原则范围查找规则等值匹配+范围查找Order By + limit 优化分组查询优化总结MySQL 是如何帮我们维护非主键索引的等值匹配原则 我们现在已经知道了如果是【主键索引】,在插入数据的时候是根据主键的顺序依次往后排列的,一个数据页不够就会分…...

布谷鸟优化算法C++
#include <iostream> #include <vector> #include <cmath> #include <random> #include <time.h> #include <fstream> #define pi acos(-1) //5只布谷鸟 constexpr int NestNum 40; //pi值 //规定X,Y 的取值范围 constexpr double X_…...
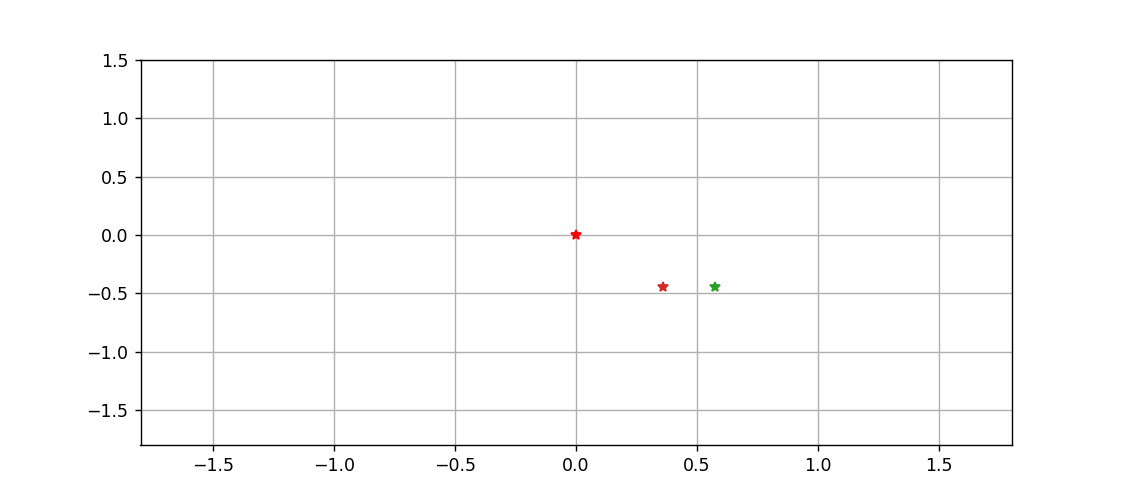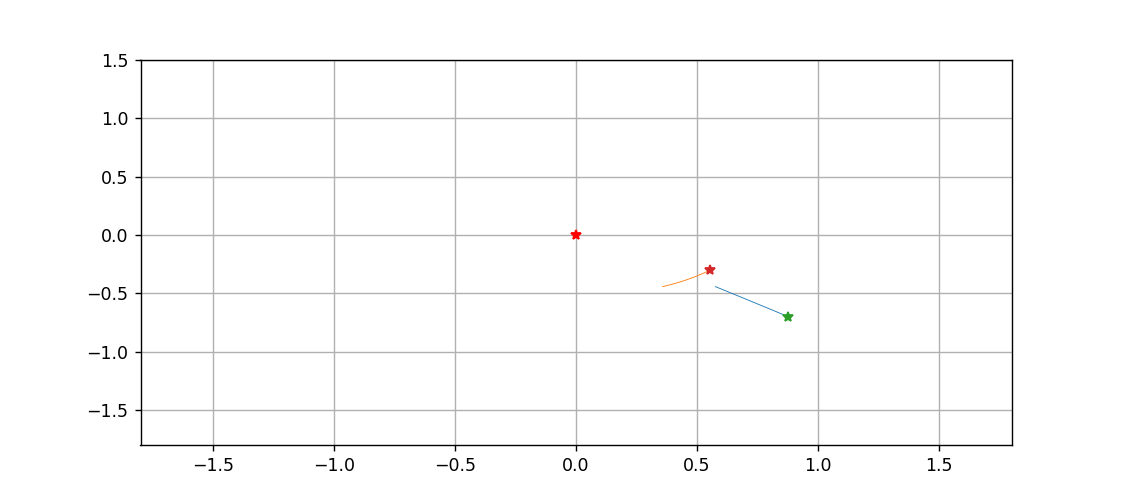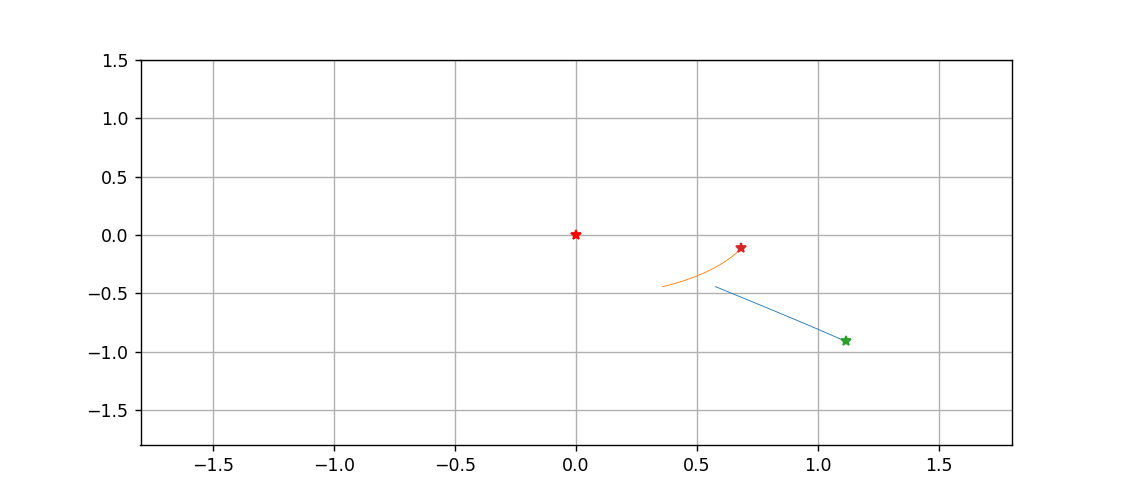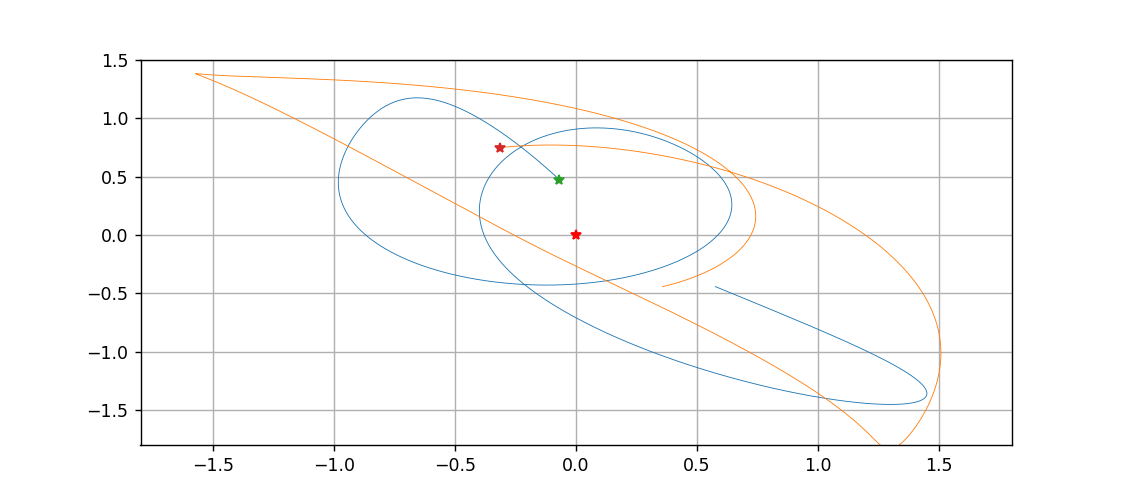
三体到底是啥?用Python跑一遍就明白了
文章目录拉格朗日方程推导方程组微分方程算法化求解画图动图绘制温馨提示,只想看图的画直接跳到最后一节拉格朗日方程 此前所做的一切三体和太阳系的动画,都是基于牛顿力学的,而且直接对微分进行差分化,从而精度非常感人…...

Golang-Hello world
目录 安装 Go(如果尚未安装) 编写Hello world 使用Golang的外部包 自动下载需要的外部包...

this指针C++
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章 🔥座右铭:“不要等到什么都没有了,才下定决心去做” …...

SpringBoot+WebSocket实时监控异常
# 写在前面此异常非彼异常,标题所说的异常是业务上的异常。最近做了一个需求,消防的设备巡检,如果巡检发现异常,通过手机端提交,后台的实时监控页面实时获取到该设备的信息及位置,然后安排员工去处理。因为…...
Baumer工业相机堡盟相机如何使用自动曝光功能(自动曝光优点和行业应用)(C++)
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

HTML、CSS学习笔记7(移动适配:rem、less)
一、移动适配 rem:目前多数企业在用的解决方案vw / vh:未来的解决方案 1.rem(单位) 1.1使用rem单位设置尺寸 px单位或百分比布局可以实现吗? ————不可以 网页的根字号——HTML标签 1.2.rem移动适配 写法&#x…...
STM32感应开关盖垃圾桶
目录 项目需求 项目框图 编辑 硬件清单 sg90舵机介绍及实战 sg90舵机介绍 角度控制 SG90舵机编程实现 超声波传感器介绍及实战 超声波传感器介绍 超声波编程实战 项目设计及实现 项目需求 检测靠近时,垃圾桶自动开盖并伴随滴一声,2秒后关盖…...

进程跟线程的区别
进程跟线程的区别 文章目录进程跟线程的区别前言一.什么线程二.线程与进程的联系三.线程与进程有什么不同前言 现代所有计算机都能同时做几件事情,当一个用户程序正在运行时,计算机还能同时读取磁盘,并向屏幕打印输出正文.在一个多道操作程序中,cpu由一道程序向另外一道程的切…...

[ICLR 2016] Unsupervised representation learning with DCGANs
目录 IntroductionModel ArchitectureReferencesIntroduction 作者提出了用 CNN 搭建 GAN,使得 GAN 训练更加稳定的一系列准则,并将满足这些设计理念的模型称为 DCGANs (Deep Convolutional GANs). 此外,作者将 trained discriminators 用于图像分类任务,相比于其他无监督算…...

QT编程从入门到精通之十五:“第五章:Qt GUI应用程序设计”之“5.1 UI文件设计与运行机制”之“5.1.2 项目管理文件”
目录 第五章:Qt GUI应用程序设计 5.1 UI文件设计与运行机制 5.1.2 项目管理文件 第五章:Qt GUI应用程序设计 在“Qt 程序创建基础”上,本章将继续深入地介绍Qt Creator设计GUI应用程序的方法...

基于Three.js和MindAR实现的网页端WebAR人脸识别追踪功能的京剧换脸Demo(含源码)
前言 近段时间一直在玩MindAR的功能,之前一直在弄图片识别追踪的功能,发现其强大的功能还有脸部识别和追踪的功能,就基于其面部网格的例子修改了一个国粹京剧的换脸程序。如果你不了解MindAR的环境配置可以先参考这篇文章:基于Mi…...

动态规划思路
拉勾教育版权所有:https://kaiwu.lagou.com/course/courseInfo.htm?courseId3 动态规划思路 1.最优子结构 2.重复计算子机构 3.依靠递归,层层向上传值,所以编程时初始化子结构很重要 动态规划步骤 1.判断动态规划的类型 1.线性规划 >&…...

HTTPS关键词语解释和简单通讯流程
1、 什么是HTTPS HTTPS是基于HTTP的上层添加了一个叫做TLS的安全层,对数据的加密等操作都是在这个安全层中进行处理的,其底层还是应用的HTTP。 2、 什么是对称加密; 加密和解密都是用同一个秘钥 3、 什么是非对称加密; 加密和…...

“前端开发中的三种定时任务及其应用“
前端定时任务是指在一定时间间隔内,自动执行指定的操作或函数。在前端开发中,定时任务被广泛应用于诸如数据更新、定时提醒、定时刷新页面等方面。在本文中,我们将介绍前端中常见的三种定时任务,分别是 setTimeout、setInterval 和…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
:LSM Tree 概述)
从零手写Java版本的LSM Tree (一):LSM Tree 概述
🔥 推荐一个高质量的Java LSM Tree开源项目! https://github.com/brianxiadong/java-lsm-tree java-lsm-tree 是一个从零实现的Log-Structured Merge Tree,专为高并发写入场景设计。 核心亮点: ⚡ 极致性能:写入速度超…...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...
无头浏览器技术:Python爬虫如何精准模拟搜索点击
1. 无头浏览器技术概述 1.1 什么是无头浏览器? 无头浏览器是一种没有图形用户界面(GUI)的浏览器,它通过程序控制浏览器内核(如Chromium、Firefox)执行页面加载、JavaScript渲染、表单提交等操作。由于不渲…...

Linux 中替换文件中的某个字符串
如果你想在 Linux 中替换文件中的某个字符串,可以使用以下命令: 1. 基本替换(sed 命令) sed -i s/原字符串/新字符串/g 文件名示例:将 file.txt 中所有的 old_text 替换成 new_text sed -i s/old_text/new_text/g fi…...

Digital IC Design Flow
Flow介绍 1.设计规格 架构师根据市场需求制作算法模型(Algorithm emulation)及芯片架构(Chip architecture),确定芯片设计规格书(Chip design specification) 原型验证 原型验证(Prototype Validation)通常位于产品开发流程的前期阶段,主要是在设计和开发的初步阶…...
