7.2 向量的坐标
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人!
🌙个人主页:阿芒的主页
⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学这门课的知识点,参考书主要为经典的同济版第七版《高等数学》以及作者在高校使用的《高等数学》系统教材。梳理《高等数学》这门课,旨在帮助那些刚刚接触这门课的小白以及需要系统复习这门课的考研人士。希望自己的一些经验能够帮助更多的人。
文章目录
- 向量的坐标表示
- 利用坐标作向量的线性运算
- 向量的模、方向角、投影
向量的坐标表示
空间直角坐标系下,任意向量r→\overrightarrow{r}r可用向径OM→\overrightarrow{OM}OM表示.
以i→\overrightarrow{i}ij→\overrightarrow{j}jk→\overrightarrow{k}k分别表示x、y、zx、y、zx、y、z轴上的单位向量,设点MMM的坐标为M(x,y,z)M(x,y,z)M(x,y,z),则
OM→\overrightarrow{OM}OM=r→\overrightarrow{r}r=xi→+yj→+zk→x\overrightarrow{i}+y\overrightarrow{j}+z\overrightarrow{k}xi+yj+zk 称为向量r→\overrightarrow{r}r的坐标分解式.
xi→,yj→,zk→x\overrightarrow{i},y\overrightarrow{j},z\overrightarrow{k}xi,yj,zk称为向量r→\overrightarrow{r}r沿三个坐标轴方向的分向量.
利用坐标作向量的线性运算
设a→=(ax,ay,az),b→=(bx,by,bz)\overrightarrow{a}=(a_{x},a_{y},a_{z}),\overrightarrow{b}=(b_{x},b_{y},b_{z})a=(ax,ay,az),b=(bx,by,bz),λ{\lambda}λ为实数,则
a→±b→\overrightarrow{a}\pm\overrightarrow{b}a±b=(ax±bx,ay±by,az±bz)(a_{x}\pm b_{x}, a_{y}\pm b_{y},a_{z}\pm b_{z})(ax±bx,ay±by,az±bz)
λa→\lambda\overrightarrow{a}λa=(λax,λay,λaz)(\lambda a_{x},\lambda a_{y},\lambda a_{z})(λax,λay,λaz)
平行向量对应坐标成比例:
当a→≠0→\overrightarrow{a}\neq\overrightarrow{0}a=0时,
a→∥b→\overrightarrow{a}\parallel\overrightarrow{b}a∥b ⟺\Longleftrightarrow⟺b→\overrightarrow{b}b=λa→\lambda\overrightarrow{a}λa(λ\lambdaλ为唯一 实数).
~~~~~~~~~~~~ ⟺\Longleftrightarrow⟺ bxax\frac{{b_{x}}}{a_{x}}axbx=byay\frac{{b_{y}}}{a_{y}}ayby=bzaz\frac{{b_{z}}}{a_{z}}azbz
向量的模、方向角、投影
-
向量的模与两点间的距离公式
-
向量的模
设r→=(x,y,z)\overrightarrow{r}=(x,y,z)r=(x,y,z),作OM→\overrightarrow{OM}OM=r→\overrightarrow{r}r,则有 ∣r→∣=∣OM→∣=x2+y2+z2|\overrightarrow{r}|=|\overrightarrow{OM}| =\sqrt{x^{2}+y^{2}+z^{2}}∣r∣=∣OM∣=x2+y2+z2 -
两点间的距离公式
设A(x1,y1,z1)A(x_{1},y_{1},z_{1})A(x1,y1,z1),B(x2,y2,z2)B(x_{2},y_{2},z_{2})B(x2,y2,z2),因为
AB→\overrightarrow{AB}AB= OB→\overrightarrow{OB}OB-OA→\overrightarrow{OA}OA=(x2−x1,y2−y1,z2−z1)(x_{2}-x_{1},y_{2}-y_{1},z_{2}-z_{1})(x2−x1,y2−y1,z2−z1),得两点间的距离公式:
∣AB∣|{AB}|∣AB∣ =∣AB→∣|\overrightarrow{AB}|∣AB∣=(x2−x1)2+(y2−y1)2+(z2−z1)2\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}(x2−x1)2+(y2−y1)2+(z2−z1)2 -
方向角与方向余弦
-
方向角
设有两非零向量 a→\overrightarrow{a}a,b→\overrightarrow{b}b,任取空间一点O, 作OA→\overrightarrow{OA}OA=a→\overrightarrow{a}a, OB→\overrightarrow{OB}OB=b→\overrightarrow{b}b 称φ=∠AOB(0≤φ≤π)\varphi=∠AOB(0 \leq \varphi \leq \pi)φ=∠AOB(0≤φ≤π)为向量a→\overrightarrow{a}a,b→\overrightarrow{b}b 的夹角.
类似可定义向量与轴,轴与轴的夹角.
给定 r→=(x,y,z)≠0→\overrightarrow{r}=(x,y,z)\neq\overrightarrow{0}r=(x,y,z)=0,称 r→\overrightarrow{r}r与三坐标轴的夹角α,β,γ\alpha,\beta,\gammaα,β,γ为其方向角 -
方向余弦
方向角的余弦称为方向余弦
cosαcos\alphacosα= x∣r→∣\frac{x}{|\overrightarrow{r}|}∣r∣x=xx2+y2+z2\frac{x}{ \sqrt{x^{2}+y^{2}+z^{2} }}x2+y2+z2x
cosβcos\betacosβ= y∣r→∣\frac{y}{|\overrightarrow{r}|}∣r∣y=yx2+y2+z2\frac{y}{ \sqrt{x^{2}+y^{2}+z^{2} }}x2+y2+z2y
cosγcos\gammacosγ= z∣r→∣\frac{z}{|\overrightarrow{r}|}∣r∣z=zx2+y2+z2\frac{z}{ \sqrt{x^{2}+y^{2}+z^{2} }}x2+y2+z2z
-
方向余弦的性质
cos2αcos^{2}\alphacos2α+cos2βcos^{2}\betacos2β+cos2γcos^{2}\gammacos2γ=1
向量r→\overrightarrow{r}r的单位向量:r→°=r→∣r→∣\overrightarrow{r}^{°}=\frac{\overrightarrow{r}}{|\overrightarrow{r}|}r°=∣r∣r=(cosα,cosβ,cosγ)(cos\alpha,cos\beta,cos\gamma)(cosα,cosβ,cosγ) -
向量在轴上的投影
-
空间一点在轴上的投影
过点AAA作轴uuu的垂直平面,交点A′A^{'}A′即为点AAA在轴uuu上的投影. -
向量在轴上的投影
设有一轴uuu,e→\overrightarrow{e}e是轴uuu上与uuu轴同向的单位向量.
已知向量AB→\overrightarrow{AB}AB的起点AAA和BBB在轴uuu上的投影分别为A′A^{'}A′和B′B^{'}B′,则A′B′→\overrightarrow{A^{'}B^{'}}A′B′称为AB→\overrightarrow{AB}AB在轴uuu上的分向量.
若A′B′→=λe→\overrightarrow{A^{'}B^{'}}={\lambda}\overrightarrow{e}A′B′=λe,则λ{\lambda}λ称为AB→\overrightarrow{AB}AB在轴uuu上的投影.
向量AB→\overrightarrow{AB}AB在轴uuu上的投影记为PrjuAB→Prj_{u}\overrightarrow{AB}PrjuAB或 (AB→)u(\overrightarrow{AB})_{u}(AB)u.
注:若a→=(ax,ay,az)\overrightarrow{a}=(a_{x},a_{y},a_{z})a=(ax,ay,az),则
ax=Prjxa→,ay=Prjya→,az=Prjza→a_{x}=Prj_{x}\overrightarrow{a},a_{y}=Prj_{y}\overrightarrow{a},a_{z}=Prj_{z}\overrightarrow{a}ax=Prjxa,ay=Prjya,az=Prjza
- 向量的投影性质
①投影性质1
向量AB→\overrightarrow{AB}AB在轴uuu上的投影等于向量的模乘以轴与向量的夹角的余弦:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ PrjuAB→Prj_{u}\overrightarrow{AB}PrjuAB=∣AB→∣cosφ|\overrightarrow{AB}|cos\varphi∣AB∣cosφ
②投影性质2
两个向量的和在轴上的投影等于两个向量在该轴上的投影之和.(可推广到任意有限个)
~~~~~~~~~~~~~~~~~~~~~~ Prju(a→1+a→2)Prj_{u}(\overrightarrow{a}_{1}+\overrightarrow{a}_{2})Prju(a1+a2)=Prjua→1+Prjua→2Prj_{u}\overrightarrow{a}_{1}+Prj_{u}\overrightarrow{a}_{2}Prjua1+Prjua2
③投影性质3
~~~~~~~~~~~~~~~~~~~~~~ Prju(λa→)Prj_{u}(\lambda\overrightarrow{a})Prju(λa)=λPrjua→\lambda Prj_{u}\overrightarrow{a}λPrjua
相关文章:

7.2 向量的坐标
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

公式编写1000问21-22
21.问: 求助——(周,日,60分钟,30分钟)MACD同时向上的公式怎么表达 答(知无不言): z:“macd.dea#week”; r:“macd.dea#day”; f:“macd.dea#min60”; f1:“macd.dea#min30”; rz:“macd.dea##week”; rr:“macd.dea##day”; rf:“…...

1041 考试座位号
每个 PAT 考生在参加考试时都会被分配两个座位号,一个是试机座位,一个是考试座位。正常情况下,考生在入场时先得到试机座位号码,入座进入试机状态后,系统会显示该考生的考试座位号码,考试时考生需要换到考试…...

2023年3月北京/广州/杭州/深圳数据治理工程师认证DAMA-CDGA/CDGP
DAMA认证为数据管理专业人士提供职业目标晋升规划,彰显了职业发展里程碑及发展阶梯定义,帮助数据管理从业人士获得企业数字化转型战略下的必备职业能力,促进开展工作实践应用及实际问题解决,形成企业所需的新数字经济下的核心职业…...
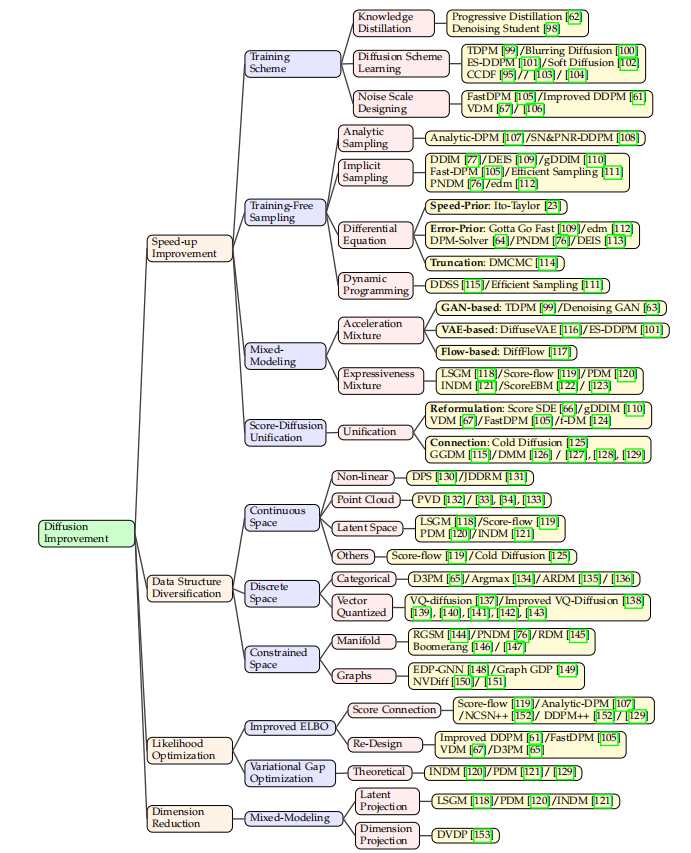
【AICG】2、扩散模型 | 到底什么是扩散模型?
文章目录一、什么是扩散模型二、扩散模型相关定义2.1 符号和定义2.2 问题规范化三、可以提升的点参考论文:A Survey on Generative Diffusion Model github:https://github.com/chq1155/A-Survey-on-Generative-Diffusion-Model 一、什么是扩散模型 已…...

高等数学——多元函数微分学
文章目录多元函数微分学多元函数的极限多元函数的连续性偏导数定义高阶偏导数全微分定义全微分存在的必要条件全微分存在的充分条件多元函数的微分法复合函数微分法隐函数微分法多元函数的极值与最值无约束极值条件极值及拉格朗日乘数法最大值最小值二重积分概念性质计算利用直…...
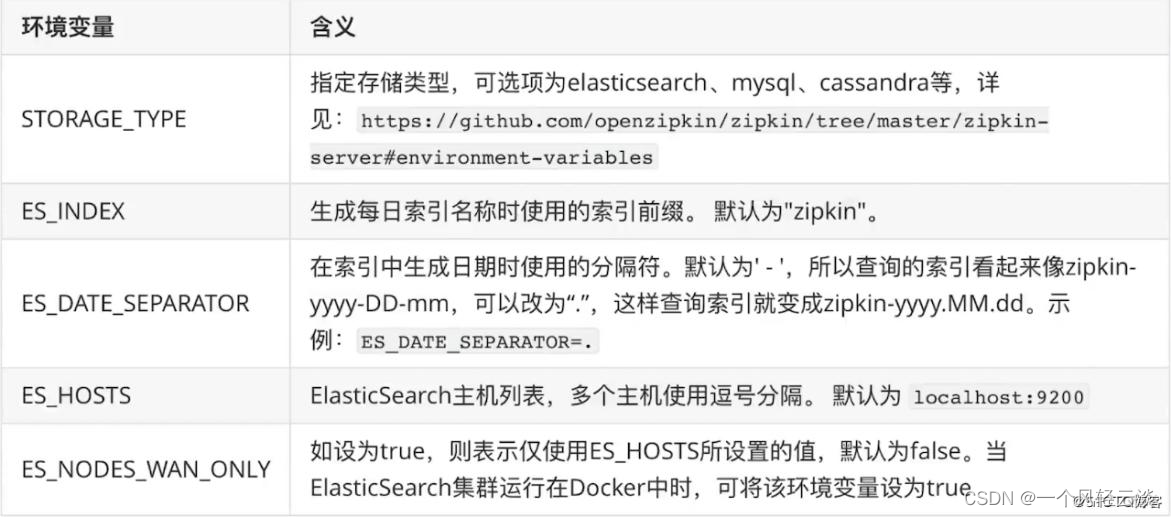
一文打通Sleuth+Zipkin 服务链路追踪
1、为什么用 微服务架构是一个分布式架构,它按业务划分服务单元,一个分布式系统往往有很多个服务单元。由于服务单元数量众多,业务的复杂性,如果出现了错误和异常,很难去定位。主要体现在,一个请求可能需要…...
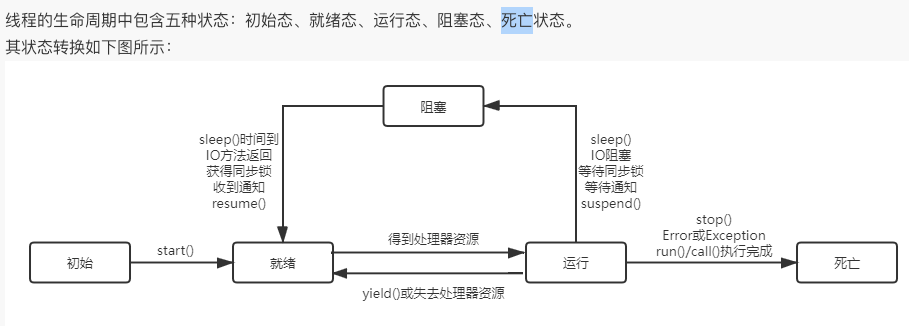
牛客刷题第一弹
1.异常处理 都是Throwable的子类: ①.Exception(异常):是程序本身可以处理的异常。 ②.Error(错误): 是程序无法处理的错误。这些错误表示故障发生于虚拟机自身、或者发生在虚拟机试图执行应用时,一般不需…...
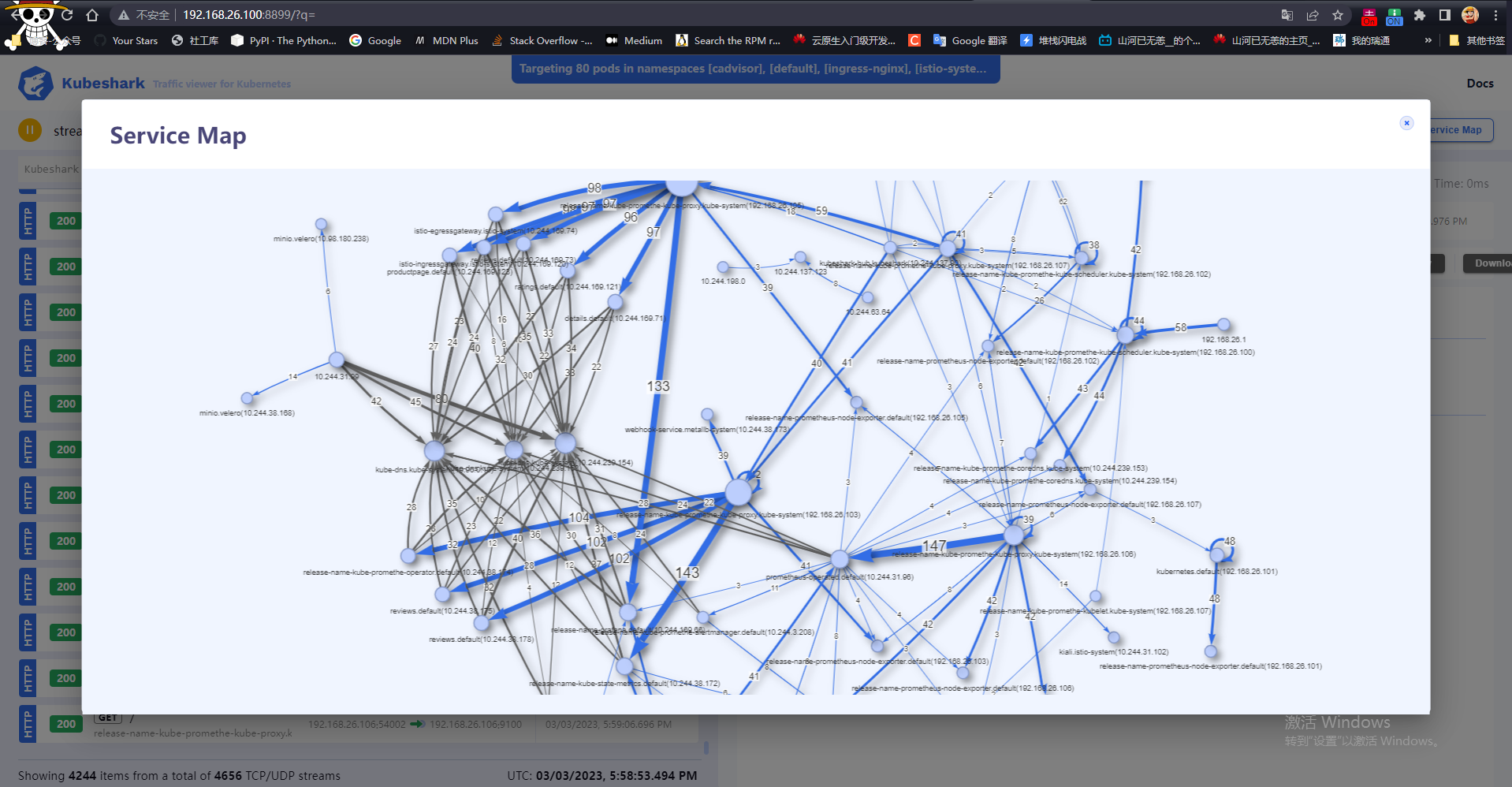
K8s:通过 Kubeshark 体验 大白鲨(Wireshark)/TCPDump 监控 Kubernetes 集群
写在前面 分享一个 k8s 集群流量查看器很轻量的一个工具,监控方便博文内容涉及: Kubeshark 简单介绍Windows、Linux 下载运行监控DemoKubeshark 特性功能介绍 理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。…...
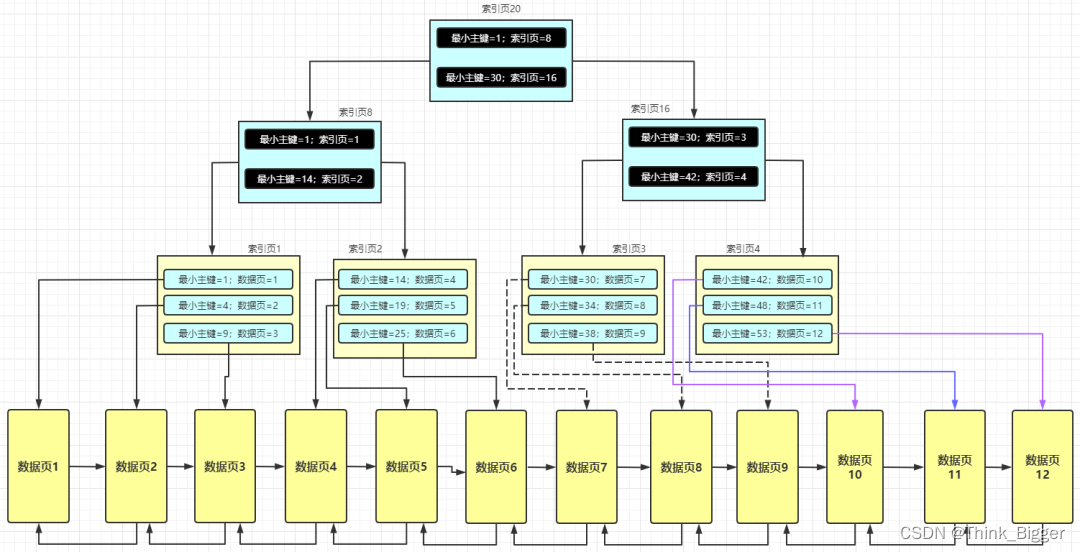
MySQL查询索引原则
文章目录 等值匹配原则最左前缀匹配原则范围查找规则等值匹配+范围查找Order By + limit 优化分组查询优化总结MySQL 是如何帮我们维护非主键索引的等值匹配原则 我们现在已经知道了如果是【主键索引】,在插入数据的时候是根据主键的顺序依次往后排列的,一个数据页不够就会分…...

布谷鸟优化算法C++
#include <iostream> #include <vector> #include <cmath> #include <random> #include <time.h> #include <fstream> #define pi acos(-1) //5只布谷鸟 constexpr int NestNum 40; //pi值 //规定X,Y 的取值范围 constexpr double X_…...
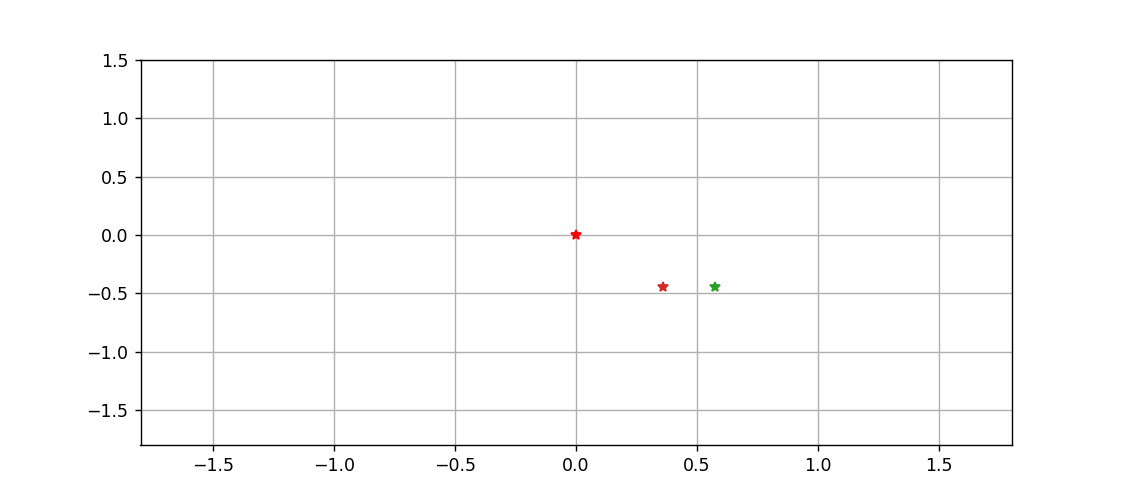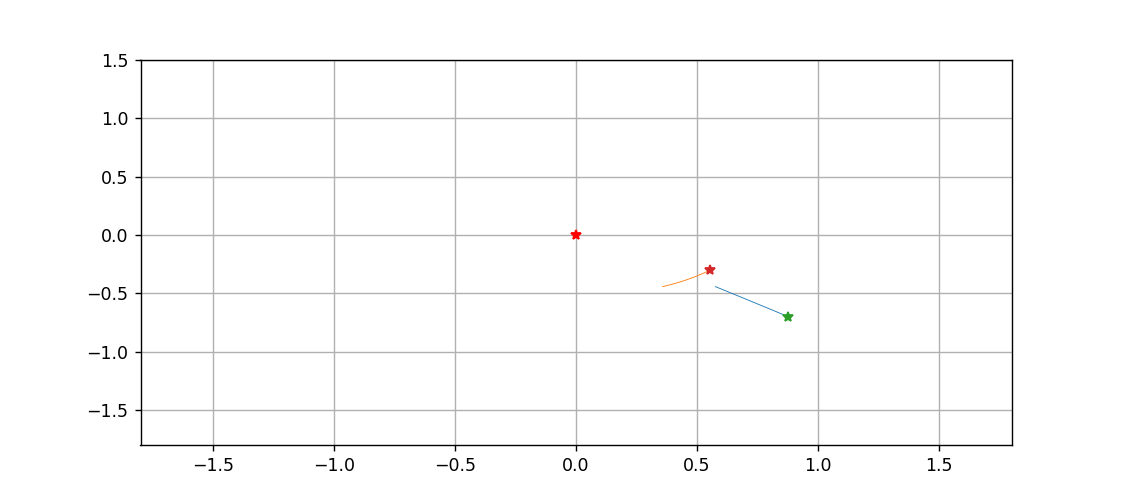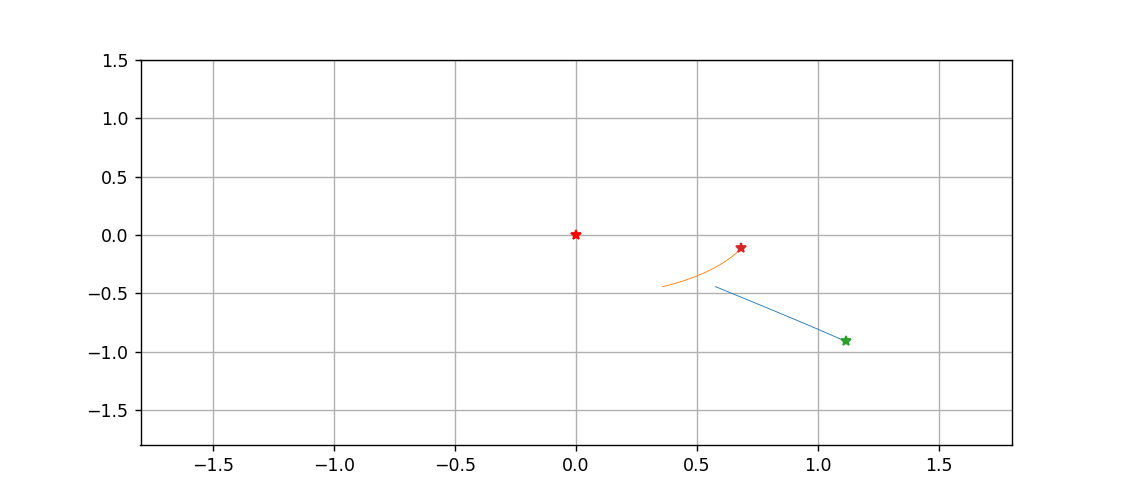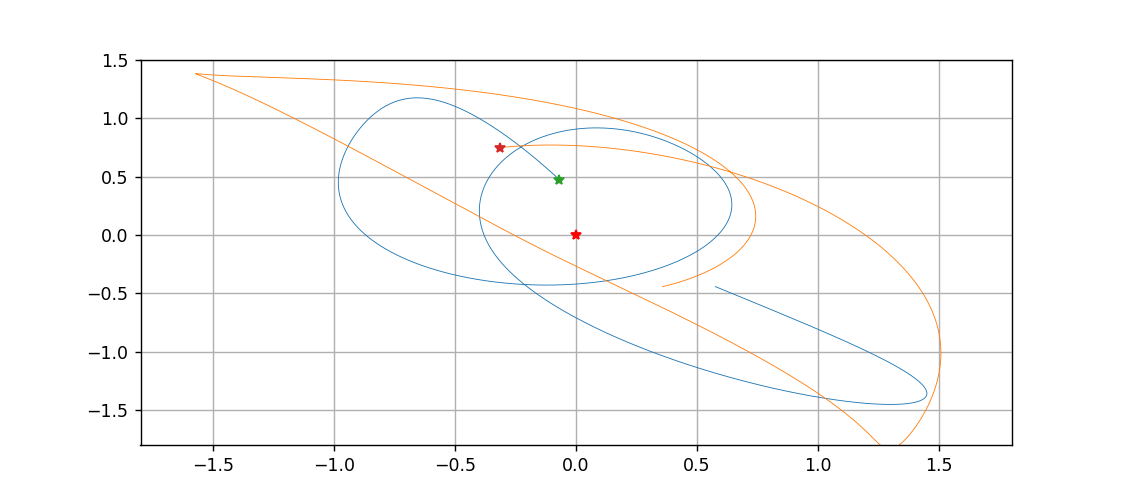
三体到底是啥?用Python跑一遍就明白了
文章目录拉格朗日方程推导方程组微分方程算法化求解画图动图绘制温馨提示,只想看图的画直接跳到最后一节拉格朗日方程 此前所做的一切三体和太阳系的动画,都是基于牛顿力学的,而且直接对微分进行差分化,从而精度非常感人…...

Golang-Hello world
目录 安装 Go(如果尚未安装) 编写Hello world 使用Golang的外部包 自动下载需要的外部包...

this指针C++
🐶博主主页:ᰔᩚ. 一怀明月ꦿ ❤️🔥专栏系列:线性代数,C初学者入门训练,题解C,C的使用文章 🔥座右铭:“不要等到什么都没有了,才下定决心去做” …...

SpringBoot+WebSocket实时监控异常
# 写在前面此异常非彼异常,标题所说的异常是业务上的异常。最近做了一个需求,消防的设备巡检,如果巡检发现异常,通过手机端提交,后台的实时监控页面实时获取到该设备的信息及位置,然后安排员工去处理。因为…...
Baumer工业相机堡盟相机如何使用自动曝光功能(自动曝光优点和行业应用)(C++)
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

HTML、CSS学习笔记7(移动适配:rem、less)
一、移动适配 rem:目前多数企业在用的解决方案vw / vh:未来的解决方案 1.rem(单位) 1.1使用rem单位设置尺寸 px单位或百分比布局可以实现吗? ————不可以 网页的根字号——HTML标签 1.2.rem移动适配 写法&#x…...
STM32感应开关盖垃圾桶
目录 项目需求 项目框图 编辑 硬件清单 sg90舵机介绍及实战 sg90舵机介绍 角度控制 SG90舵机编程实现 超声波传感器介绍及实战 超声波传感器介绍 超声波编程实战 项目设计及实现 项目需求 检测靠近时,垃圾桶自动开盖并伴随滴一声,2秒后关盖…...

进程跟线程的区别
进程跟线程的区别 文章目录进程跟线程的区别前言一.什么线程二.线程与进程的联系三.线程与进程有什么不同前言 现代所有计算机都能同时做几件事情,当一个用户程序正在运行时,计算机还能同时读取磁盘,并向屏幕打印输出正文.在一个多道操作程序中,cpu由一道程序向另外一道程的切…...

[ICLR 2016] Unsupervised representation learning with DCGANs
目录 IntroductionModel ArchitectureReferencesIntroduction 作者提出了用 CNN 搭建 GAN,使得 GAN 训练更加稳定的一系列准则,并将满足这些设计理念的模型称为 DCGANs (Deep Convolutional GANs). 此外,作者将 trained discriminators 用于图像分类任务,相比于其他无监督算…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
