机器学习数学原理专题——线性分类模型:损失函数推导新视角——交叉熵
目录
二、从回归到线性分类模型:分类
3.分类模型损失函数推导——极大似然估计法
(1)二分类损失函数——极大似然估计
(2)多分类损失函数——极大似然估计
4.模型损失函数推导新视角——交叉熵
(1)信息量和系统熵
(2)相对熵(KL散度)与交叉熵
(3)回归损失函数——交叉熵视角
(4)二分类损失函数——交叉熵视角
(5)多分类损失函数——交叉熵视角
二、从回归到线性分类模型:分类
在上一篇文章中,我们推导了从回归模型到分类模型的“中介”——链接函数,下面在此基础上,同回归模型逻辑一样,进一步推导分类模型的损失函数。
3.分类模型损失函数推导——极大似然估计法
在回归损失函数的推导中,我们引入了极大似然估计的方法,从概率论的角度得到和最小二乘法一样的结论,这样的推导为损失函数的设置提供了更严谨的数学理论支持。极大似然估计法同样可以推广到分类模型,下面先对之前回归中的估计流程进行一个概括(下述以回归为例)。
极大似然估计推导损函流程(以回归为例):
1.模型假设分布 : 高斯分布
2.误差项的分布 : 均值为 0 的正态分布
3.y 的似然概率 : 正态分布概率密度函数
4.写出似然函数 : 所有样本 y 似然连乘
5.极大似然估计公式推导 : 取对数取负
根据上述流程,首先推导二分类问题的损失函数形式。
(1)二分类损失函数——极大似然估计
①二分类的误差分布与假设分布
分类问题与回归问题最显著的一个差异是模型输出的样式。不同于回归的实数输出,二分类问题的标签 和模型预测
的输出要么是 0,要么是 1 。因此可以直接枚举出实际标签和模型预测只可能有四种确定的情况,如下表所示。
| 误差 | ||||
| 样本数量 |
样本数总和为 ,
。可以看到误差项取值只有两种可能:对应要么模型预测正确,误差为零;要么模型预测错误,误差为一。通过上述表格,可以看出误差项服从伯努利分布,并且可以根据表格中统计的出现频率近似估计这一分布的参数:
——正类样本发生概率。即可以得到误差项分布,也对应于二分类问题的假设分布。
②标签 y 的似然概率
在回归中,我们通过正态分布的线性组合性质推出 y 的具体分布。这实际是用模型输出来估计真实标签高斯分布的均值参数 。其中的数学原理在回归推导损失函数章节详细解释。
,其中
二分类同理,模型的输出 估计的是伯努利分布中的参数
。因此可以直接写出 y 的在模型输出
作为参数下的分布具体形式。
根据伯努利分布的密度函数,可以计算写出 y 取不同值的具体概率。对于二分类问题,真实标签 和模型输出
都只有两种取值情况。因此可以将两种分类情况写成一个式子概括。
③似然函数与极大似然估计
上述有了单个样本的分类似然概率值函数,那么对应于二分类问题的似然函数,就是将所有样本的似然值乘积起来得到,遇到出现当前所有样本取值情况的总的发生概率值。而极大似然估计朴素的想法就是,既然出现了当前的采样结果,就证明当前这个情况在“所有情况”中发生的概率应该最大,因此我们通过最大化之前乘积的概率,可以得到相关参数的估计值。
样本中正类样本的概率为 ,得到所有样本发生概率如下。
在似然估计中,我们用模型的输出 来近似估计正类样本概率
。
进一步知道模型的输出 是由模型参数
决定的(因为特征矩阵
对于每个样本是固定的),而模型参数就是我们需要去优化的部分。同时为了数值稳定,还需求取平均。因此可以得到二分类问题优化所需的损失函数如下。
(2)多分类损失函数——极大似然估计
同二分类一样的逻辑,这里不再赘述。区别是在其似然函数的数学表达上。对于 n 个分类的问题,对应 n 个不同的概率取值。可以用一种“独热编码”的方式来表达。
我们可以“创建”一个 n 维的向量,对于真实的分类标签来说,其对应的分类可以用 n 维向量的对应索引位置取 1 来表达。
模型的输出同样也是一个 n 维的向量,具体来讲,其是一个概率的向量空间,每个值对应该位置对应分类的概率取值。
那么对于上述给出真实标签分类的样本,其给定 x() 对 y 的似然如下。
可以发现,对于当前样本其概率取值只需取出其真实分类的类别下,模型预测的该类别概率值即可。因此可以用元素取值的方式将上述连乘归纳为一个式子,其代表对应独热编码中的索引取出预测概率的值(这也是为什么要用独热编码来标记不同类别的原因:这样使得下述式子连乘)可以推广到所有样本。
那么根据极大似然估计的思想,我们将所有类别的样本对应于当前模型的概率值连乘起来,就是当前模型预测所有采样结果整体发生概率的评估值。通过最大化这个值,可以优化我们模型的参数 了。
其中, 代表第 i 个类别采样的样本数,
对于小批次 个训练样本,假设每个类别都只有一个样本,那么似然函数可以简化。
使用极大似然估计法得到多分类的损失函数。
4.模型损失函数推导新视角——交叉熵
使用极大似然估计法推到模型损失函数的方法总结来说是,先根据假设分布得出关于 X 似然函数,再将从实际分布中随机抽样的变量 X 值代入似然函数得到关于所有样本的总的似然。最终得到的似然是一个值,它代表的是实际分布中的变量在假设分布下得到的概率,换句话说极大似然估计是通过概率值的角度比较了实际和假设分布的差异,其目的是为了通过参数变化使假设分布不断逼近实际分布。
因为实际分布和假设分布不是同一种分布,因此我们不能直接比较其分布对应的参数,如两个高斯分布可以通过比较其均值方差的差异来判断分布的差距。回归中实际分布是一个均匀分布,假设分布是个高斯分布。因此才使用极大似然估计这一“下策”来衡量分布差异。
这样得到的损失函数,其实本质是在衡量假设分布和实际分布的“差距”——当假设分布和实际分布差异很大时,用实际分布的变量在假设分布下计算的概率应很小(因此需要极大化似然函数);差异小时,概率很大。而极大化的优化过程就是通过模型参数W的变换来改变假设分布中的一些变量。
模型参数 W 隐含在模型输出中,再通过链接函数与假设分布中的一些参数相关。如回归高斯分布中的均值,二分类中的正样样本概率值
,多分类问题中每类的概率
。
因此我们推到损失函数关心的关键点就是找到一种衡量假设分布和实际分布差异的指标,交叉熵视角下,也是延用了这一概率论的思想——从信息论的角度比较两个分布的差异。
(1)信息量和系统熵
引入信息量的概率并将其量化为数学公式。
①信息量和概率存在反比关系。
现实生活中小概率事件总“让人着迷”,这也是因为小概率事件包含的信息量更大。就比如股市上未来大涨或大跌的消息包含的信息量更大,因为大多数情况股市都是一个区间的波动,而突然的大涨大跌都是小概率事件,其背后往往蕴藏着机遇或危机。又或者如猜明星游戏中告知姓氏就比告知性别信息量更大,因为性别只有男女,即二分之一的概率值;而姓氏则是在百家姓中的选择,随机猜中的概率更小。
由此,我们可以初步定义一个最简单的数学关系式描述上述关系,在后续逐步完善。设信息量用字母 表示,事件的概率用
表示。
上述式子显然没有很好的描述概率和信息量的关系,一个最特殊的例子是,必然事件(概率)的信息量应该为零(
),比如“太阳东升”这一表述就没有什么信息量对于一个有常识的人来说,因为总所周知,也就是日常说的“废话”。这表明信息量与概率的数学关系没有这么简单,应该存在一个函数关系。
②信息量具有乘积化加的性质。
举例来说,假设场景为从工厂生产的甲、乙、丙、丁四种产品中抽取次品检测,A信息是抽取甲、乙、丙、丁概率分别为 、
、
、
;B信息是抽到是甲产品,甲为次品的概率为
;C信息是直接表示从工厂生产的两种产品中抽到甲产品是次品的概率是
。
例子中最后一个C信息在信息量的角度是A信息和B信息的总和,因为抽到甲次品需要先确定抽到的是甲产品,其次还要确定其为次品。同时,A信息和B信息描述的事件是独立的,因此概率上和C信息具有乘积等式关系。将上述表述用数学式子归纳如下。
第一个式子表示信息量的和关系,第二个式子表示概率的乘积关系。由此可推出以下等式。
这表明对于计算信息量的函数 ,其应该满足上述式子中内部乘积可拆开为独立求和,可以推断,基础函数中
应是信息量函数的合理选择。
目前为止,已知的信息量计算函数式子如下。
③信息量与二进制的关系。
知道是 log 函数还不够,还需清楚其底数。这需要信息编码角度重新审视,我们先从一个简单的例子开始,再过渡到之前找次品的例子。
现在有A、B、C、D四个等可能的事件(它们发生概率都为 )。假设现在只有0、1两个数(二进制)来表述信息,通过其排列组合,我们可以将四个事件用编码的方式用数字表示。最短编码的长度为2。
| 事件 | A | B | C | D |
| 编码 | 00 | 01 | 10 | 11 |
| 概率 | 1/4 | 1/4 | 1/4 | 1/4 |
当事件数量增加——八个等可能事件时,最短编码长度为3。
| 事件 | A | B | C | D | E | F | G | H |
| 编码 | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| 概率 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
当事件都是等可能时,用最“粗暴”的方法就是给所有的可能性都编码,所以对于均匀分布来说,其编码的可能性就是其概率的倒数,设编码长度为 ,均匀分布概率为
,可得等式如下。
此时得到了和上一步相同的信息计算函数形式,并且得到了底数的具体意义——用多少进制来编码数据:底数为2代表使用二进制;底数为3代表使用三进制....
让我们回到稍复杂一点的找次品的例子,其事件发生概率不再是等可能的情况了,此时该如何编码。一种简单的方法是直接按可能情况编码,如对于A信息只有四种情况:抽到甲、抽到乙、抽到丙或抽到丁。这样编码和一个四个等可能事件编码没有区别。
| 事件 | A | B | C | D |
| 概率 | 1/4 | 1/4 | 1/4 | 1/4 |
| 次品事件 | 抽到甲 | 抽到乙 | 抽到丙 | 抽到丁 |
| 概率 | 1/2 | 1/4 | 1/8 | 1/8 |
| 编码 | 00 | 01 | 10 | 11 |
但这样编码“效率是低的”,对于“高频”发生的事件——抽到甲(概率 ),将其和其他低概率发生的事件编码一样长度是不合理的,有没有更好的编码方式?我们可以按其各自发生概率值根据编码长度(信息量)计算公式来定其长度。如下表所示。
| 次品事件 | 抽到甲 | 抽到乙 | 抽到丙 | 抽到丁 |
| 概率 | 1/2 | 1/4 | 1/8 | 1/8 |
| 编码长度 | ||||
| 编码(√) | 1 | 00 | 010 | 011 |
| 编码(×) | 0 | 00 | 010 | 011 |
需注意,抽到甲编码应和后续编码第一个数字区分开,不然将难以区分开是抽到甲的信息未传输完还是其他情况,最后一行给出了这种错误的编码方式。
对上述编码方式求其关于概率的加权平均长度如下,设平均编码长度 ,不同情况的概率和其对应计算的编码长度分别为
。
这要比原先简单的将所有可能视为等概率编码使用更少的开销。因此可以归纳出一般的计算任意一个离散分布的信息量计算公式(实际上推广到连续分布情况,只需将求和符合变为积分)
上述计算公式得到的不总是一个整数,因此称其为编码“长度”不那么严谨了。这里引入一个新的名词系统熵,也是信息熵——,其代表的是关于分布的平均编码长度。
(2)相对熵(KL散度)与交叉熵
有了信息熵的计算定义以后,回想我们最初引入信息量和熵概率的目的是,找到一个“指标”可以定量衡量两个概率分布的差别,从而可以计算机器学习模型参数代表的分布和实际我们希望机器学习到的现实的分布之前的差异。信息熵的计算得到的值可以代表分布的混乱程度,也是其包含的信息量。因此很自然的,我们关心两个分布信息熵的差值。
一种最直接的方法就是计算假设模型的信息熵减去实际分布的信息熵就好了。但是问题在于,实际分布的情况好说,假设模型的分布由于是存在于“我们脑海里”的一种假设,它的采样概率真实是多少我们无从得知,最多从这个假设算出其可能的“编码长度”,即这个假设包含了多少的信息量。
下面详细看一下信息熵计算公式 中的
,它其实需要拆分成两半。一半是用作加权求和的权值的概率
,一半是用于计算事件所需编码长度的概率
。这么做也对应了前面说的,假设分布的权值概率(采样概率)
是未知的。
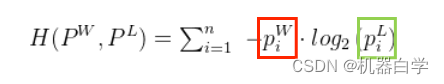
上述计算信息熵的式子实际是计算一个分布每个概率值对应的编码长度,最后加权求期望。回到之前抽次品的例子,我们能计算出最短的平均编码长度(也就是对抽到的是哪个产品这一事件的分布编码),是因为我们在题干中以“上帝视角”给出了所有情况对应的概率。而现实中,我们不可能把工厂所有产品都检测一遍,我们只能抽样出小批量的样本。
基于这个背景,此时出现了两种概率——假设分布的概率 (心里预期估计的概率)& 实际分布的概率
(实际采样得到的概率)
下面举例说明,假设检测次品中抽样产品类型——甲乙丙丁,小批量独立随机的抽出10件产品。实际抽出的结果即其对应的实际概率分布如下。
| 抽样结果 | 甲 | 丙 | 乙 | 甲 | 甲 | 乙 | 丁 | 乙 | 乙 | 甲 |
| 采样事件 | 甲 | 乙 | 丙 | 丁 |
| 实际分布概率 | 2/5 | 2/5 | 1/10 | 1/10 |
| 求和权值 | 2/5 | 2/5 | 1/10 | 1/10 |
| 编码长度 |
假设分布(即我们自己脑海里猜测的甲乙丙丁的概率——也可以理解为机器学习模型参数推测的概率分布),现在给出两个不同的假设——1.假设同之前题目中给出的概率分布情况一样;2.四个事件等概率发生。
题目概率的假设分布
| 假设事件 | 甲 | 乙 | 丙 | 丁 |
| 假设分布概率 | 1/2 | 1/4 | 1/8 | 1/8 |
| 求和权值 | ? | ? | ? | ? |
| 编码长度 |
等概率的假设分布
| 假设事件 | 甲 | 乙 | 丙 | 丁 |
| 假设分布概率 | 1/4 | 1/4 | 1/4 | 1/4 |
| 求和权值 | ? | ? | ? | ? |
| 编码长度 |
实际和假设分布的关键区别就在于,假设分布就好比说“明天有多大概率下雨”,我们只能去衡量这句话包含了多少的信息量(编码长度),而无法知道明天到底会不会下雨(求和权值)。
于是,有了一种替代方案——不用假设分布和实际分布的绝对熵来衡量差异,使用相对熵( KL散度)来替换衡量两个分布的关系。
下面给出本节重点的 KL 散度定义式,并由其推出我们想要的交叉熵表示式。
其实KL散度很简单,既然只是假设分布的求和权值不知道,那么就用已知的实际分布权值代替使用不就好了。因此 KL 散度中一定有一个基准分布,如本例中将实际分布(小批量抽样的结果概率)视为基准,可以得到 KL 散度衡量下的,两个分布的相似度为
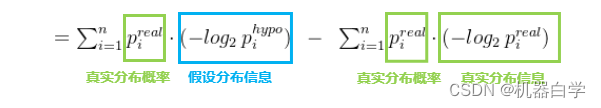
KL散度衡量的是两个分布系统的相似程度。因此这个值越小越好,值越小,假设分布和真实分布越相似,趋于0时,两个分布几乎一致了。
首先讨论之前给出的两个假设分布对应的 KL 散度值。
对于题目给出概率的假设分布,根据公式可以计算得到它和真实的抽样分布的相似度如下。 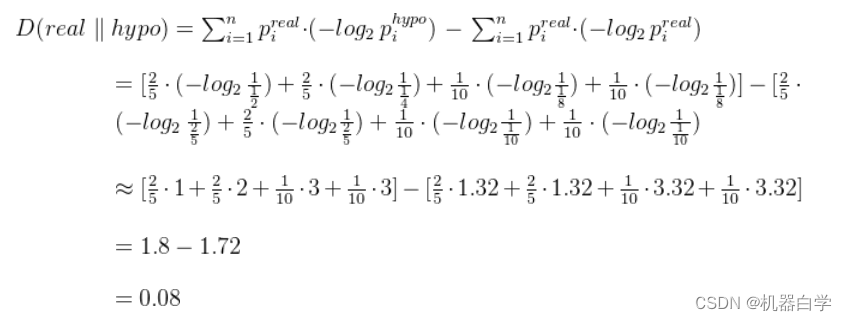
对于等概率的假设分布,根据公式可以计算得到它和真实的抽样分布的相似度如下。
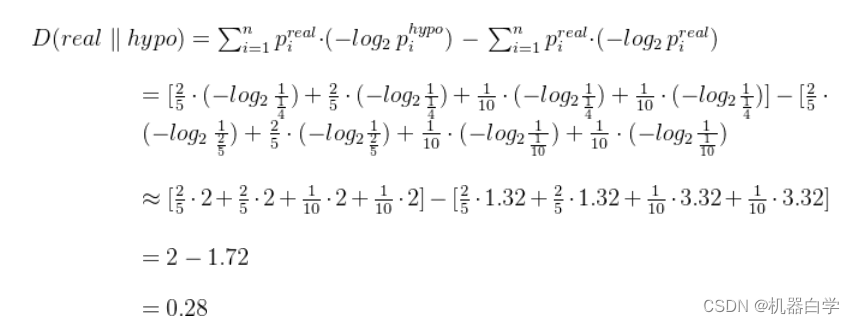
可以看到题干给出的概率分布比等概率分布的假设计算的 KL 散度更小,说明题干概率更接近真实的分布状况。很自然的联想到,机器学习的模型参数训练过程就是从一个随机的参数(等概率假设分布)不断优化到接近真实的样本分布(题干概率分布) 。那么我们就需要极小化 KL 散度(这得在KL散度计算是一个正数的前提下,可以证得,此处省略)。
回到 KL 散度计算式,由于真实分布的权值概率和信息量已知且固定,因此绿色后式实际是一个“常数”,而前式中蓝色部分会根据假设分布的不同而变化。因此在极小化过程中,常数可以省略,仅保留“变化部分”。
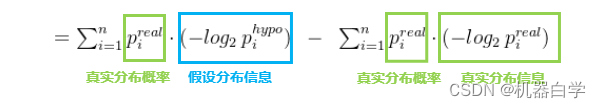
由此比较假设分布和实际分布的相似度,可简化用一个式子表示,上面前半部分就是交叉熵。下面定义数学表达式。

(3)回归损失函数——交叉熵视角
有了交叉熵衡量分布相似度后,我们就可以定义一个“损失函数”来不断优化模型的预测分布不断逼近真实的样本分布。现在我们用交叉熵的计算视角,重新推导回归模型的损失函数。
首先我们假设了回归模型的假设分布为高斯分布(正态分布),其分布均值为模型输出;其采样的训练数据集满足随机独立抽样,因此真实分布为均匀分布,分布的概率为样本总数的倒数
。
根据交叉熵的分量求和运算,由于假设分布和真实分布都是连续的,因此要写出其对应的概率密度,均匀分布的概率密度简单;假设分布只需将模型参数代入正态分布概率密度函数即可。
因此可以得到假设分布和真实分布概率。
代入交叉熵计算式,化简得到交叉熵视角下的回归损失函数。
之前极大似然估计中已经说明正态分布的方差 不是我们关心的重点,可以省略。
为常数可以省略。因此得到了和之前推导的一致的均方误差损失函数。极小化这一损失函数,就是极小化假设分布和真实分布的差异。
(4)二分类损失函数——交叉熵视角
二分类问题只有两种情况,真实分布就是这两类样本在总样本中的比例关系。同时二分类两个概率和为1,因此只需知道正类样本概率 y , 即可推出负类概率为 1-y 。假设分布为伯努利分布,且其概率参数在链接函数下和模型输出相关。
代入交叉熵计算式,化简得到交叉熵视角下的二分类损失函数。
由二分类问题的定义可知, 即伯努利分布的参数其实就是模型的预测输出,代入交叉熵式子中可化简得下式。
(5)多分类损失函数——交叉熵视角
多分类与二分类并无本质区别,难懂点在于符号上,在极大似然估计法中我们并没有深入解释那些符号运算的推导,现在举例说明,关键是人为巧妙的引入了“独热编码”的方式。
不失一般性,假设一个三分类问题,简单起见,每个类别有一个样本,对应有模型对其预测,我们可以将这里的训练真实样本分布和模型预测的假设分布,按之前的表格形式写下来。
| 类别 | A | B | C |
| 独热编码 | [ 1, 0, 0 ] | [ 0, 1, 0 ] | [ 0, 0, 1 ] |
| 模型预测 | [ 0.7, 0.2, 0.1 ] | [ 0.1, 0.8, 0.1 ] | [ 0.2, 0.2, 0.6 ] |
经过独热编码以后对于每个类别的交叉熵都可以用权值求和的形式计算交叉熵。
| 类别 | 交叉熵 |
| A | |
| B | |
| C |
这样的编码方式让我们发现,计算一个样本的交叉熵值时,其实就是对这个类别下模型预测的概率求其信息量(因为对应的真实分布中标签值为 “1”),其余的类别都不需要去管他们,这在优化过程中也是合理的,代表看到当前类别的特征值输入,就要在当前类别的概率预测输出上越大越好。
由于不管样本取的是哪个类别,真实分布都取的是 “1” 这个特殊值,这个巧妙的设计使得我们无需去管交叉熵中真实分布的概率,只需要取出假设分布即模型输出中对应于真实标签的预测概率值即可。
特别注意,此处的 中都是向量元素,不是幂次运算,而是从
中取出对应类别的元素值。
由此得到和极大似然法一致的损失函数形式。
相关文章:
机器学习数学原理专题——线性分类模型:损失函数推导新视角——交叉熵
目录 二、从回归到线性分类模型:分类 3.分类模型损失函数推导——极大似然估计法 (1)二分类损失函数——极大似然估计 (2)多分类损失函数——极大似然估计 4.模型损失函数推导新视角——交叉熵 (1&#x…...

windows和linux路径斜杆转换脚本,打开即用
前言: windows和linux的目录路径斜杆是相反的,在ssh或者其他什么工具在win和ubuntu传文件时候经常需要用到两边的路径,有这个工具就不用手动去修改斜杆反斜杠了。之前有个在线网站,后来挂了,就想着自己搞一个脚本来用。…...

在Android系统中,查看apk安装路径
在Android系统中,应用通常安装在内部存储的特定目录下。要找到已安装应用的路径,可以通过ADB(Android Debug Bridge)工具来查询。以下是一些步骤和命令,可以帮助你找到应用的安装路径: 使用pm list package…...

管理不到位,活该执行力差?狠抓这4点要素,强化执行力
管理不到位,活该执行力差?狠抓这4点要素,强化执行力 一:强化制度管理 1、权责分明,追责管理 要知道,规章制度其实就是一种“契约”。 在制定制度和规则的时候,民主一点,征求团队成员…...

应届毕业之本科简历制作
因为毕设以及编制岗位面试,最近好久没有更新了,刚好有同学问如何制作简历,我就准备将我自己制作简历的流程分享给各位,到此也算是一个小的结束,拿了工科学位证书毕业去做🐂🐎了。 简历主要包含内…...
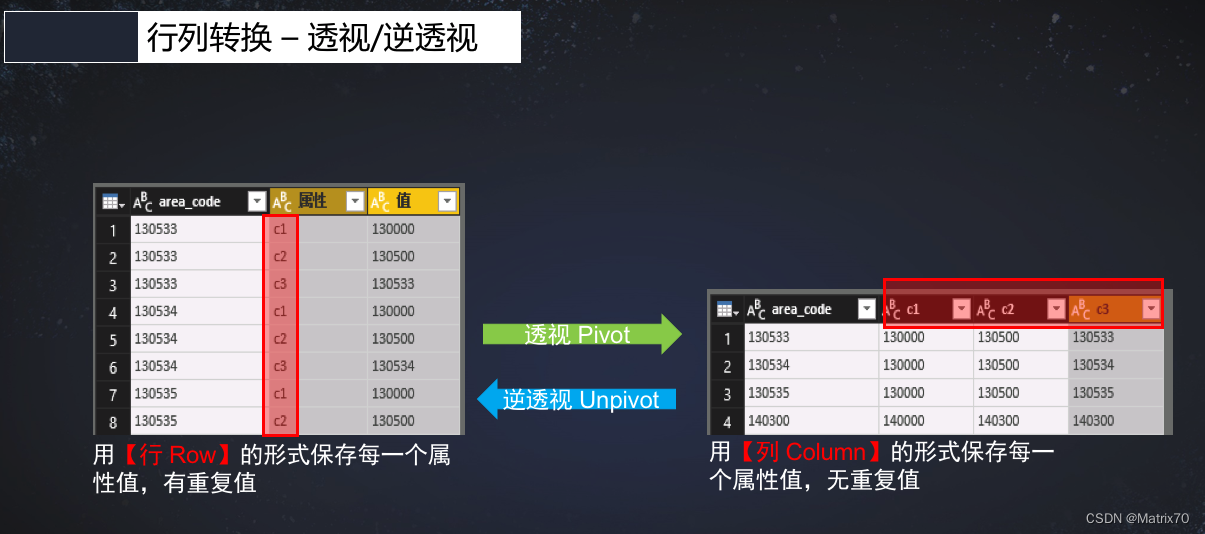
SparkOnHive_列转行、行转列生产操作(透视和逆透视)
前言 行专列,列转行是数开不可避免的一步,尤其是在最初接触Hive的时候,看到什么炸裂函数,各种udf,有点发憷,无从下手,时常产生这t怎么搞,我不会啊? 好吧ÿ…...

【人机交互 复习】第2章 Hadoop
一、概念 1.Hadoop 是一个能够对大量数据进行分布式处理的软件框架,并 且是以一种可靠、高效、可伸缩的方式进行处理的, 2.特点: 高可靠性,高效性,高可扩展性,高容错性 运行在Linux平台上,支持…...

国产自研编程语言“仓颉”来了!
在 6.21 召开的华为开发者大会(HDC2024)上,华为自研的国产编程语言“仓颉”终于对外正式发布了! 随着万物互联以及智能时代的到来,软件的形态将发生巨大的变化。一方面,移动应用和移动互联网领域仍然强力驱动人机交互…...

Swarm 集群管理
Swarm 集群管理 简介 Docker Swarm 是 Docker 的集群管理工具。它将 Docker 主机池转变为单个虚拟 Docker 主机。 Docker Swarm 提供了标准的 Docker API,所有任何已经与 Docker 守护程序通信的工具都可以使用 Swarm 轻松地扩展到多个主机。 支持的工具包括但不限…...

从社交网络到元宇宙:Facebook的战略转型
随着科技的迅猛发展和数字化时代的深入,社交网络已不再局限于简单的信息交流和社交互动,而是逐步向更广阔、更深远的虚拟现实空间——元宇宙(Metaverse)转变。作为全球最大的社交网络平台之一,Facebook正在积极推动这一…...
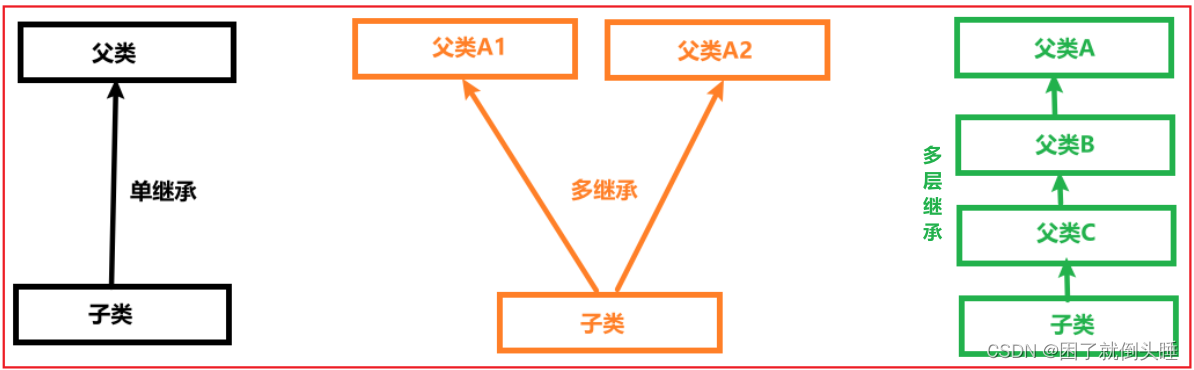
程序猿大战Python——面向对象——继承进阶
方法重写 目标:掌握方法的重写。 当父类的同名方法达不到子类的要求,则可以在子类中对方法进行重写。语法: class 父类名(object):def 方法A(self):代码... class 子类名(父类名):def 方法A(self):代码... 例如,一起来完成&…...
【Linux基础】SSH登录
SSH简介 安全外壳协议(Secure Shell Protocol,简称SSH)是一种加密的网络传输协议,可在不安全的网络中为网络服务提供安全的传输环境。 SSH通过在网络中建立安全隧道来实现SSH客户端与服务器之间的连接。 SSH最常见的用途是远程登…...

经典机器学习方法(7)—— 卷积神经网络CNN
参考:《动手学深度学习》第六章 卷积神经网络(convolutional neural network,CNN)是一类针对图像数据设计的神经网络,它充分利用了图像数据的特点,具有适合图像特征提取的归纳偏置,因而在图像相…...

经典面试题【作用域、闭包、变量提升】,带你深入理解掌握!
前言:哈喽,大家好,我是前端菜鸟的自我修养!今天给大家分享经典面试题【作用域、闭包、变量提升】,并提供具体代码帮助大家深入理解,彻底掌握!原创不易,如果能帮助到带大家࿰…...
Dockerfile实战
Dockerfile是用来快速创建自定义镜像的一种文本格式的配置文件,在持续集成和持续部署时,需要使用Dockerfile生成相关应用程序的镜像。 Dockerfile常用命令 FROM:继承基础镜像MAINTAINER:镜像制作作者的信息,已弃用&a…...

常用的开源数据集网站
Kaggle(https://www.kaggle.com/datasets):Kaggle 是一个著名的数据科学竞赛平台,也提供了大量的开放数据集供用户下载和使用。UCI Machine Learning Repository(https://archive.ics.uci.edu/datasets)&am…...

html文本被木马病毒植入vbs脚本
我在公司服务器上写了一个静态html,方便导航,结果没过多久发现html文件被修改了,在</html>标签后加了这些代码。 注:WriteData 的内容很长,被我删掉了很多,不然没法提交这个提问 <SCRIPT Lan…...

jsonl 文件介绍
jsonl文件介绍 什么是 jsonl 文件文件结构读取jsonl文件写入jsonl文件 什么是 jsonl 文件 jsonl(json lines)是一种文件格式,其中每一行都是一个单独的 json 对象。与常规的 json文件不同,jsonl文件在处理大量数据时具有优势&…...

反射机制详解
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏:Java从入门到精通 ✨特色专栏ÿ…...
【数据库】七、数据库安全与保护
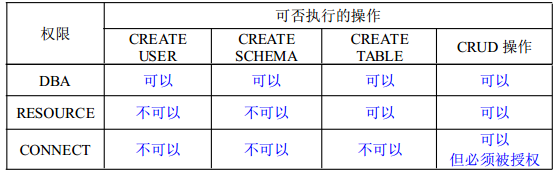
七、数据库安全与保护 文章目录 七、数据库安全与保护安全性访问控制数据库安全性控制用户标识和鉴别存取控制自主存取控制(DAC)存取控制方法:授权与回收GRANT授权REVOKE回收 强制存取控制(MAC) MySQL的安全设置用户管理1.创建登录用户2.修改用户密码3.修改用户名4.…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
