昇思25天学习打卡营第6天|函数式自动微分
函数式自动微分
相关前置知识复习
深度学习的重点之一是神经网络。而神经网络很重要的一环是反向传播算法,这个算法用于调整神经网络的权重。
反向传播算法
这里举例说明反向传播在做什么。
假设你是一个学生,一次考试过后,你收到了一份老师打分后的试卷。
前向传播就是考试的过程,你通过自己学习的知识来解答试卷上的每个问题。这就是用神经网络的权重(已有的知识)推理(解答)输入数据(问题),得到预测结果(最终的答卷)。
计算误差是你评估自己答案和标准答案的差距。这里在神经网络中是使用损失函数来衡量预测结果和实际结果之间的差距。
反向传播是分析错误的问题,分析具体是哪个知识点没掌握清楚,再去针对性的学习对应的知识,加强弱项。这里在申请网络中就是使用误差来反向调整神经网络中的权重。
反向传播的步骤是:
- 前向传播:输入数据通过神经网络计算出预测结果
- 计算误差:通过神经网络的预测结果和实际结果,计算损失函数
- 反向传播:将误差从输出层向输入层反向传播,计算每一层的误差。
- 调整权重:根据计算出的误差,使用优化算法(如梯度下降)调整每一层的权重,以减少误差。
链式法则
链式法则(Chain Rule)是微积分的重要概念,用于计算复合函数的导数。这是计算梯度的基础。简单来说链式法则的基本思想是将复杂的过程分解成多个简单的部分,再将各部分的结果组合起来得到总结果。
假设我们有两个函数
f f f和 g g g,并且它们是复合的,即 y = f ( g ( x ) ) y=f(g(x)) y=f(g(x))。根据链式法则,复合函数
y y y 对 x x x 的导数可以表示为: d y d x = d y d g ⋅ d g d x \frac{d_y}{d_x}= \frac{d_y}{d_g} \cdot \frac{d_g}{d_x} dxdy=dgdy⋅dxdg
为什么要在神经网络这里强调链式法则呢?
举个小例子。想象神经网络的结构,第一层传给第二层,第二层传给第三层,每一层的输出都是后一层的输入,整个就是一条链。通过最后一层的输出,计算损失函数对最终输出的导数,再根据链式法则,可以逐层往前推导梯度,将误差从输出层传递回输入层,计算出每个参数的梯度,再进行参数更新,完成反向传递。
自动微分
上面阐述了,神经网络的误差需要通过链式法则传递,从而计算出每个参数的梯度。自动微分利用链式法则自动计算反向传播的梯度,也就是将梯度计算过程变得自动化了。
构建模型
以下我们构建一个简单的线性模型来介绍如何进行函数式自动微分。
普通的线性模型: y = w × b + b y = w \times b+ b y=w×b+b
输入x,输出y,通过调整w和b参数来优化预测。
# 环境配置
import numpy as np
import mindspore
from mindspore import nn
from mindspore import ops
from mindspore import Tensor, Parameter
x = ops.ones(5, mindspore.float32) # 形状为5的全1输入
y = ops.zeros(3, mindspore.float32) # 形状为3的全0输出
w = Parameter(Tensor(np.random.randn(5, 3), mindspore.float32), name='w') # 线性函数的权重
b = Parameter(Tensor(np.random.randn(3,), mindspore.float32), name='b') # 线性函数的偏差
def function(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss
解读一下这段代码:
z是线性函数的组合,ops.matmul(x, w) 是输入x和权重w的矩阵乘法,然后再将偏置向量b加入到结果中。
这里使用binary_cross_entropy_with_logits作为损失函数。这个函数计算了预测值和目标值之间的二值交叉熵损失。
通过 f u n c t i o n ( x , y , w , b ) function(x,y,w,b) function(x,y,w,b)可以计算到loss值。
模型参数优化
为了优化模型参数,需要计算对两个参数的导数。
- ∂ loss ∂ w \frac{\partial \operatorname{loss}}{\partial w} ∂w∂loss
- ∂ loss ∂ b \frac{\partial \operatorname{loss}}{\partial b} ∂b∂loss
这里使用mindspore.grad函数,来获得function的微分函数用以计算梯度。
grad函数包括两个参数:
- fn:待求导的函数。
- grad_position:需要求导的参数的索引。
function的入参是x,y,w,b, 我们需要对w,b求导。w,b在入参中的索引是2,3。因此grad_postion为(2,3),可得function的微分函数
grad_fn = mindspore.grad(function, (2, 3))
停止梯度
一般来讲,只会求loss对参数的导数,因此只需要输出loss就可以。但如果要求的话,也可以输出多个loss以外的参数。在我们的例子里,也就是在function的函数中增加除了loss之外的输出值。
def function_with_logits(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss, zgrad_fn = mindspore.grad(function_with_logits, (2, 3))
grads = grad_fn(x, y, w, b)
这里增加了对z的输出。在后续grad_fn调用时,z也会参与到梯度计算,对w和b的梯度结果造成影响。
stop gradient用以阻止某些张量的梯度计算。通俗的说,当对张量 z 应用 Stop Gradient 操作后,在反向传播过程中,其梯度会被置零,从而不会影响之前的计算。具体操作如下:
def function_stop_gradient(x, y, w, b):z = ops.matmul(x, w) + bloss = ops.binary_cross_entropy_with_logits(z, y, ops.ones_like(z), ops.ones_like(z))return loss, ops.stop_gradient(z)
这样的函数定义下,函数依然输出z,但是对z进行了阻断,不会影响到后续梯度计算是对其他参数(w,b)更新。
Auxiliary data
Auxiliary data意思是辅助数据,是函数第一个输出以外的其他输出。一般loss是第一个输出,其他都是Auxiliary data。
has_aux指具有辅助数据,可以在grad函数中设置,就能自动将辅助数据添加stop gradient操作。
grad_fn = mindspore.grad(function_with_logits, (2, 3), has_aux=True)
神经网络实现自动微分
上面的操作是自己手动搭建了一个模型。在之前的章节中我们使用nn.Cell构建了神经网络,现在来看看如何在Cell模型中如何实现函数式自动微分。
初始化模型
# 模型初始化,定义参数w和b,并构建模型
class Network(nn.Cell):def __init__(self):super().__init__()self.w = wself.b = bdef construct(self, x):z = ops.matmul(x, self.w) + self.breturn z
# 实例化模型
model = Network()
# 定义损失函数
loss_fn = nn.BCEWithLogitsLoss()
# 定义前向计算函数
def forward_fn(x, y):z = model(x)loss = loss_fn(z, y)return loss
# 上面的步骤之前的文章已经介绍过了。
这里我们使用value_and_grad接口获得微分函数。w、b两个参数已经是网络属性的一部分了,因此不需要再次进行指定了,而是使用model.trainable_params()获取可求导的参数。
grad_fn = mindspore.value_and_grad(forward_fn, None, weights=model.trainable_params())
总结
本章使用了两种方式实现了自动微分,也就是梯度计算。一种是手动构建模型,一种使用nn.Cell搭建的神经网络。此外,本节也复习了一些深度学习的基础知识
打卡凭证

相关文章:

昇思25天学习打卡营第6天|函数式自动微分
函数式自动微分 相关前置知识复习 深度学习的重点之一是神经网络。而神经网络很重要的一环是反向传播算法,这个算法用于调整神经网络的权重。 反向传播算法 这里举例说明反向传播在做什么。 假设你是一个学生,一次考试过后,你收到了一份老…...

作业7.2
用结构体数组以及函数完成: 录入你要增加的几个学生,之后输出所有的学生信息 删除你要删除的第几个学生,并打印所有的学生信息 修改你要修改的第几个学生,并打印所有的学生信息 查找你要查找的第几个学生,并打印该的学生信息 1 /*…...
)
PCL 点云聚类(基于体素连通性)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里的思路很简单,我们通过将点云转换为体素,基于体素的连通性实现对点云的聚类(有点类似于欧式聚类),不过这种方式进行的聚类有些粗糙,但聚类速度相对会快很多,具体的实现效果可以详细阅读代码。 二、实现代…...
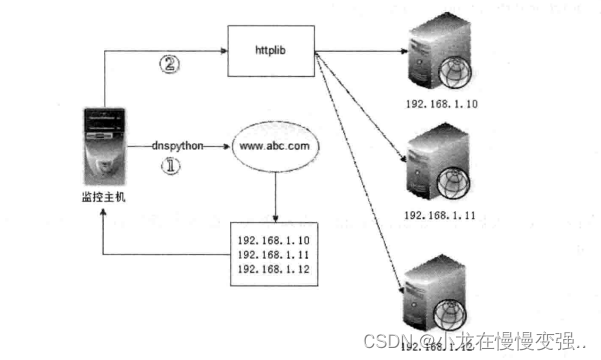
python自动化运维--DNS处理模块dnspython
1.dnspython介绍 dnspython是Pyhton实现的一个DNS工具包,他几乎支持所有的记录类型,可以用于查询、传输并动态更新ZONE信息,同事支持TSIG(事物签名)验证消息和EDNS0(扩展DNS)。在系统管理方面&a…...

成人职场商务英语学习柯桥外语学校|邮件中的“备注”用英语怎么说?
在英语中,"备注"通常可以翻译为"Notes" 或 "Remarks"。 这两个词在邮件中都很常用。例如: 1. Notes Notes: 是最通用和最常见的表达,可以用在各种情况下,例如: 提供有关电子邮件内容的附加信息 列…...

AndroidStudio报错macMissing essential plugin
电脑重启后打开studio: Missing essential plugin: org.jetbrains.android Please reinstall Android Studio from scratch. 无法使用 对应Mac下disabled_plugins.txt位于如下目录: /Users/ACB/Library/Application Support/Google/AndroidStudio4.2 …...

doris集群物理部署保姆级教程
doris物理安装 1、安装要求 Linux 操作系统版本需求 查看CentOs版本(>7.1) cat /etc/redhat-release 1)设置系统最大打开文件句柄数 vi /etc/security/limits.conf soft nofile 65536hard nofile 65536 echo ‘’’ soft nofile 655360hard nofile 655…...
探囊取物之多形式登录页面(基于BootStrap4)
基于BootStrap4的登录页面,支持手机验证码登录、账号密码登录、二维码登录、其它统一登录 低配置云服务器,首次加载速度较慢,请耐心等候;演练页面可点击查看源码 预览页面:http://www.daelui.com/#/tigerlair/saas/pr…...

【ONLYOFFICE】| 桌面编辑器从0-1使用初体验
目录 一. 🦁 写在前面二. 🦁 在线使用感受2.1 创建 ONLYOFFICE 账号2.2 编辑pdf文档2.3 pdf直接创建表格 三. 🦁 写在最后 一. 🦁 写在前面 所谓桌面编辑器就是一种用于编辑文本、图像、视频等多种自媒体的软件工具,具…...
)
20、PHP字符串的排列(含源码)
题目: PHP字符串的排列? 描述: 输入一个字符串,按字典序打印出该字符串中字符的所有排列。 例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。 输入描述: 输入一个字符串,长度不超过9(可…...

Linux 标准IO的fopen和fclose
getchar(),putchar() ‐‐‐‐ 一个字符 gets(buf),puts(buf) ‐‐‐‐ 一串字符 scanf(),printf() ‐‐‐‐ 一个字符,一串字符都可以 fopen函数的形式 FILE * fopen(constchar *path , cost char *mode) /* * description : 打开一个文件 * param ‐ path…...

一个计算密集小程序在不同CPU下的表现
本文比较了几款CPU对同一测试程序的比较结果,用的是Oracle公有云OCI上的计算实例,均分配的1 OCPU,内存用的默认值,不过内存对此测试程序运行结果不重要。 本文只列结果,不做任何评价。下表中,最后一列为测…...

圈子系统搭建教程,以及圈子系统的功能特点,圈子系统,允许二开,免费源码,APP小程序H5
圈子是一款社区与群组的交友工具。你可以在软件内创造一个兴趣的群组从而达到按圈子来交友的效果用户可以根据自己的兴趣爱好。 1. 创建圈子 轻松创建专属圈子,支持付费型社群。 2. 加入圈子 加入不同圈子,设置不同名片,保护隐私。 3. 定…...
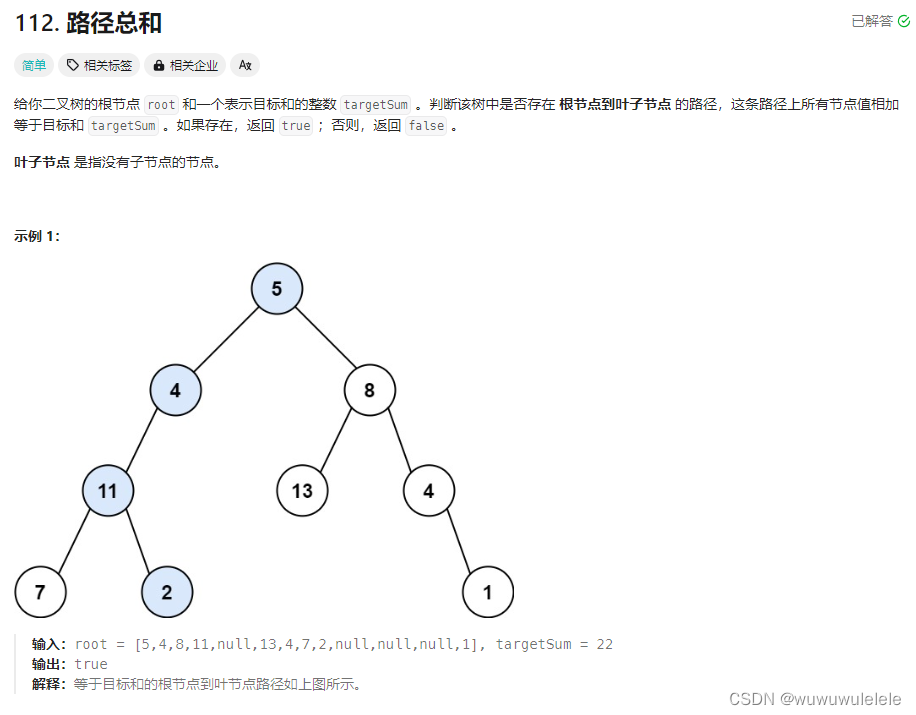
递归算法练习
112. 路径总和 package Tree;import java.util.HashMap; import java.util.Map;class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val val;} }/*** 求 树的路径和* <p>* 递归 递减* <p>* 询问是否存在从*当前节点 root 到叶…...

WebDriver 类的常用属性和方法
目录 🎍简介 🎊WebDriver 核心概念 🎉WebDriver 常用属性 🎁WebDriver 常用方法 🐷示例代码 🎪注意事项 🎐结语 🧣参考资料 🎍简介 Selenium WebDriver 是一个用…...

基于x86+FPGA+AI轴承缺陷视觉检测系统,摇枕弹簧智能检测系统
一、承缺陷视觉检测系统 应用场景 轴类零件自动检测设备,集光、机、软件、硬件,智能图像处理等先进技术于一体,利用轮廓特征匹配,目标与定位,区域选取,边缘提取,模糊运算等算法实现人工智能高…...

短剧小程序系统cps分销开发搭建
短剧小程序系统CPS分销开发搭建是一个相对复杂但具有广阔商业前景的过程。以下是关于短剧小程序系统CPS分销开发搭建的详细步骤和要点: 需求分析与市场调研: 深入了解市场需求、用户画像和竞品分析,明确产品定位和功能需求。研究目标用户的消…...

代理IP的10大误区:区分事实与虚构
在当今的数字时代,代理已成为在线环境不可或缺的一部分。它们的用途广泛,从增强在线隐私到绕过地理限制。然而,尽管代理无处不在,但仍存在许多围绕代理的误解。在本博客中,我们将探讨和消除一些最常见的代理误解&#…...

数组-长度最小的子数组
M长度最小的子数组(leetcode209) /*** param {number} target* param {number[]} nums* return {number}*/ var minSubArrayLen function(target, nums) {const n nums.length;let ans n 1;let sum 0; // 子数组元素和let left 0; // 子数组…...

深度学习之交叉验证
交叉验证(Cross-Validation)是一种用于评估和验证机器学习模型性能的技术,尤其是在数据量有限的情况下。它通过将数据集分成多个子集,反复训练和测试模型,以更稳定和可靠地估计模型的泛化能力。常见的交叉验证方法有以…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
