Python骨架肌体运动学数学模型
🎯要点
🎯运动学矢量计算 | 🎯跳远的运动学计算 | 🎯关节肢体运动最小加加速度模型 | 🎯膝关节和踝关节角度二维运动学计算 | 🎯上下肢体关节连接运动链数学模型 | 🎯刚体连接点速度加速度计算 | 🎯刚体变换二维三维运动学计算 | 🎯奇异值分解算法刚体变换 | 🎯三维运动角速度计算 | 🎯肌体和步态模型
📜Python,R,C++/C#和MATLAB运动学刚体动力学用例
📜Python重力弹弓流体晃动微分方程模型和交直流电阻电容电路
📜Python和R概率统计算法建模评估气象和运动
📜Python流体数据统计模型和浅水渗流平流模型模拟
📜Python自行车六自由度飞行器多连接件非线性运动方程模型
📜Python协作运动机器人刚体力学解耦模型
📜ROS2(Cpp或Python)机器学习路径选择三维模拟平衡车及YOLOv8视觉消息
📜Python | C++ | MATLAB机器人正逆向运动学动力学求解器及算法
📜Python | C# | MATLAB 库卡机器人微分运动学 | 欧拉-拉格朗日动力学 | 混合动力控制
📜C++和Python蚂蚁搬食和蚊虫趋光性和浮标机群行为算法神经网络
📜Python人形机踊跃跨栏举重投篮高维数动作算法模型
📜MATLAB和Python发那科ABB库卡史陶比尔工业机器人模拟示教框架
📜MATLAB雨刮通风空调模糊器和发电厂电力聚变器卷积神经
🍪语言内容分比


🍇Python运动学可视化
运动学是力学的一个分支,涉及物体的运动,而不考虑引起运动的力。给定一个描述粒子位置矢量随时间变化的方程,就可以计算各种运动学属性。最重要的是速度和加速度。如果粒子沿直线运动,则运动是直线运动。类似地,沿着弯曲路径行进的粒子也进行曲线运动。
x x x、 y y y 和 z z z 笛卡尔坐标系定义了粒子在欧几里得空间中的空间位置。方程 1 显示了粒子位置随时间的变化。秒 (s) 是时间单位,米 (m) 是位置单位。
r ⃗ ( t ) = x ( t ) ı ^ + y ( t ) ȷ ^ + z ( t ) k ^ ( 1 ) \vec{r}(t)=x(t) \hat{\imath}+y(t) \hat{\jmath}+z(t) \hat{k}\qquad(1) r(t)=x(t)^+y(t)^+z(t)k^(1)
曲率半径 (rho) 是从粒子 P 到路径 C 的曲率中心的距离。当粒子在空间中移动时,曲率半径会根据描述运动的函数而变化。
速度是由方程 2 表示的位置的一阶导数。速度矢量与粒子的轨迹相切。
v ⃗ ( t ) = d x ( t ) d t ı ^ + d y ( t ) d t ȷ ^ + d z ( t ) d t k ^ ( 2 ) \vec{v}(t)=\frac{d x(t)}{d t} \hat{\imath}+\frac{d y(t)}{d t} \hat{\jmath}+\frac{d z(t)}{d t} \hat{k}\qquad(2) v(t)=dtdx(t)^+dtdy(t)^+dtdz(t)k^(2)
该方向上的单位矢量是单位切矢量,由公式 3 给出。它等于速度矢量除以幅值。
u ^ t = v ⇀ v ( 3 ) \hat{u}_t=\frac{\stackrel{\rightharpoonup}{v}}{v}\qquad(3) u^t=vv⇀(3)
向量有方向和大小。公式 4 显示了如何计算 3 维位置矢量的大小。它可以应用于任何向量并扩展到任意数量的维度。
∥ r ⃗ ∥ = r = x 2 + y 2 + z 2 ( 4 ) \|\vec{r}\|=r=\sqrt{x^2+y^2+z^2}\qquad(4) ∥r∥=r=x2+y2+z2(4)
加速度是位置的二阶导数或速度的一阶导数。法向分量和切向分量包括加速度。
- 切向加速度与速度方向相同。
- 法向加速度是朝着粒子路径的曲率中心的方向。
方程 5 显示了加速度的两个分量。单位切向加速度矢量和法向加速度矢量是正交单位矢量。因此,它们形成一个称为密切平面的平面。
a ⃗ ( t ) = a t u ^ t ⏟ 切向 + a n u ^ n ⏟ 法向 ( 5 ) \vec{a}(t)=\underbrace{a_t \hat{u}_t}_{\text {切向 }}+\underbrace{a_n \hat{u}_n}_{\text {法向 }}\qquad(5) a(t)=切向 atu^t+法向 anu^n(5)
单位副法向量垂直于密切平面,构成右手正交系。因此,方程 6 给出了单位副法线。
u ^ b = u ^ t × u ^ n = v ⃗ × a ⃗ ∥ v ⃗ × a ⃗ ∥ ( 6 ) \hat{u}_b=\hat{u}_t \times \hat{u}_n=\frac{\vec{v} \times \vec{a}}{\|\vec{v} \times \vec{a}\|}\qquad(6) u^b=u^t×u^n=∥v×a∥v×a(6)
单位法线指向曲率中心,这意味着曲率中心 C 位于密切平面内。因此,相对于粒子 P,曲率中心 C 由方程 7 给出。
r ⃗ c / p = ρ u ^ n ( 7 ) \vec{r}_{c / p}=\rho \hat{u}_n\qquad(7) rc/p=ρu^n(7)
向量相加给出了 C 的位置向量,如公式 8 所示。
r ⃗ c = r ⃗ + r ⃗ c / p ( 8 ) \vec{r}_c=\vec{r}+\vec{r}_{c / p}\qquad(8) rc=r+rc/p(8)
Python模拟三维运动学
模拟从 0 秒开始,360 秒后结束。以下代码显示了时间线束参数。
t0 = 0
tf = 720
dt = 1
time = np.arange(t0, tf, dt, dtype='float')
方程 9 定义了粒子的位置如何随时间变化,从而定义了轨迹。
r ⃗ ( t ) = sin ( 3 t ) ı ^ + cos ( t ) ȷ ^ + cos ( 2 t ) k ^ ( 9 ) \vec{r}(t)=\sin (3 t) \hat{\imath}+\cos (t) \hat{\jmath}+\cos (2 t) \hat{k}\qquad(9) r(t)=sin(3t)^+cos(t)^+cos(2t)k^(9)
以下显示了该符号运动方程以及速度和加速度导数的声明。还提出了切向加速度方程,它是速度大小的导数。
t = sp.symbols('t')
R = [sp.cos(t), sp.sin(t), t / 5]
V = vector_derivative(R, t)
A = vector_derivative(V, t)
At = vector_magnitude(V).diff(t)
矢量方程
def vector_derivative(vector, wrt):return [component.diff(wrt) for component in vector]def vector_magnitude(vector):magnitude = 0for component in vector:magnitude += component ** 2return magnitude ** (1 / 2)def unit_vector(from_vector_and_magnitude=None, from_othogonal_vectors=None, from_orthogonal_unit_vectors=None):if from_vector_and_magnitude is not None:vector_a, magnitude = from_vector_and_magnitude[0], from_vector_and_magnitude[1]return [component / magnitude for component in vector_a]if from_othogonal_vectors is not None:vector_a, vector_b = from_othogonal_vectors[0], from_othogonal_vectors[1]vector_normal = np.cross(vector_a, vector_b)return unit_vector(from_vector_and_magnitude=(vector_normal, vector_magnitude(vector_normal)))if from_orthogonal_unit_vectors is not None:u1, u2 = from_orthogonal_unit_vectors[0], from_orthogonal_unit_vectors[1]return np.cross(u1, u2)def evaluate_vector(vector, time_step):numerical_vector = [float(component.subs(t, time_step).evalf()) for component in vector]magnitude = vector_magnitude(numerical_vector)return numerical_vector, magnitude
定义了相关的矢量函数后,就可以开始随时间传播。以下显示了用于运行模拟的代码。
propagation_time_history = []for ti in time:ti_r = d2r(ti)r, r_mag = evaluate_vector(R, ti_r)v, v_mag = evaluate_vector(V, ti_r)v_theta = [r2d(angle) for angle in direction_angles(v, v_mag)]a_theta = [r2d(angle) for angle in direction_angles(a, a_mag)]ut = unit_vector(from_vector_and_magnitude=(v, v_mag))ub = unit_vector(from_othogonal_vectors=(v, a))un = unit_vector(from_orthogonal_unit_vectors=(ub, ut))at = float(At.subs(t, ti_r).evalf())rc = r + (rho * un)rc_mag = vector_magnitude(rc)iteration_results = {'t': ti, 'rx': r[0], 'ry': r[1], 'rz': r[2], 'r_mag': r_mag,'vx': v[0], 'vy': v[1], 'vz': v[2], 'v_mag': v_mag,'rcx': rc[0], 'rcy': rc[1], 'rcz': rc[2], 'rc_mag': rc_mag, 'rho': rho,'ax': a[0], 'ay': a[1], 'az': a[2], 'a_mag': a_mag, 'an': an, 'at': at,'ubx': ub[0], 'uby': ub[1], 'ubz': ub[2],'utx': ut[0], 'uty': ut[1], 'utz': ut[2],'unx': un[0], 'uny': un[1], 'unz': un[2]}propagation_time_history.append(iteration_results)df = pd.DataFrame(propagation_time_history)👉参阅&更新:计算思维 | 亚图跨际
相关文章:

Python骨架肌体运动学数学模型
🎯要点 🎯运动学矢量计算 | 🎯跳远的运动学计算 | 🎯关节肢体运动最小加加速度模型 | 🎯膝关节和踝关节角度二维运动学计算 | 🎯上下肢体关节连接运动链数学模型 | 🎯刚体连接点速度加速度计算…...
)
二叉树的序列化和反序列化(Java)
概述 关于面试中常见的其他二叉树算法题,参考面试算法之二叉树(Java)。二叉树的定义(注意到有使用lombok提供的两个注解): lombok.Data lombok.AllArgsConstructor private static class TreeNode {private TreeNode left;priva…...

Java中的泛型类
Java中的泛类 Java 的泛型(Generics)是一种语言特性,允许你定义类、接口和方法时使用类型参数。这使得代码更具可读性和安全性,因为编译器能够在编译时检查类型,而不是在运行时。 泛型类 定义泛型类时,可…...

57、Flink 的项目配置概述
1)概览 1.开始 要开始使用 Flink 应用程序,请使用以下命令、脚本和模板来创建 Flink 项目。 可以使用如下的 Maven 命令或快速启动脚本,基于原型创建一个项目。 a)Maven 命令 mvn archetype:generate \-Darch…...

零基础自学爬虫技术该从哪里入手?
零基础学习Python并不一定是困难的,这主要取决于个人的学习方法、投入的时间以及学习目标的设定。Python是一门相对容易入门的编程语言,它有着简洁的语法、丰富的库和广泛的应用领域(如数据分析、Web开发、人工智能等),…...

Vue.js 基础入门指南
前言 在前端开发的广阔领域中,Vue.js 无疑是一颗璀璨的明星,以其渐进式框架的特性吸引了无数开发者的目光。Vue.js 旨在通过简洁的 API 实现响应式的数据绑定和组合的视图组件,使得构建用户界面变得既快速又简单。本文将带你走进 Vue.js 的世…...

山泰科技集团陈玉东:争当数字化时代的知识产权卫士
随着互联网和数字技术的飞速普及,大版权时代已经悄然到来。在这个新时代,信息的传播速度、广度和深度均达到了前所未有的高度,极大地拓展了人们的精神世界和知识视野。然而,这一科技发展的浪潮也为版权保护带来了前所未有的挑战。…...
WBCE CMS v1.5.2 远程命令执行漏洞(CVE-2022-25099)
前言 CVE-2022-25099 是一个影响 WBCE CMS v1.5.2 的严重安全漏洞,具体存在于 /languages/index.php 组件中。该漏洞允许攻击者通过上传精心构造的 PHP 文件在受影响的系统上执行任意代码。 技术细节 受影响组件:/languages/index.php受影响版本&…...

鸿蒙语言基础类库:【@ohos.url (URL字符串解析)】
URL字符串解析 说明: 本模块首批接口从API version 7开始支持。后续版本的新增接口,采用上角标单独标记接口的起始版本。开发前请熟悉鸿蒙开发指导文档:gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 导入…...

【AutoencoderKL】基于stable-diffusion-v1.4的vae对图像重构
模型地址:https://huggingface.co/CompVis/stable-diffusion-v1-4/tree/main/vae 主要参考:Using-Stable-Diffusion-VAE-to-encode-satellite-images sd1.4 vae 下载到本地 from diffusers import AutoencoderKL from PIL import Image import torch import to…...
)
《警世贤文》摘抄:守法篇、惜时篇、修性篇、修身篇、待人篇、防人篇(建议多读书、多看报、少吃零食多睡觉)
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/140243440 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
vue2+element-ui新增编辑表格+删除行
实现效果: 代码实现 : <el-table :data"dataForm.updateData"border:header-cell-style"{text-align:center}":cell-style"{text-align:center}"><el-table-column label"选项字段"align"center&…...

Day05-组织架构-角色管理
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1.组织架构-编辑部门-弹出层获取数据2.组织架构-编辑部门-编辑表单校验3.组织架构-编辑部门-确认取消4.组织架构-删除部门5.角色管理-搭建页面结构6.角色管理-获取数…...

【LLM】二、python调用本地的ollama部署的大模型
系列文章目录 往期文章: 【LLM】一、利用ollama本地部署大模型 目录 文章目录 前言 一、ollama库调用 二、langchain调用 三、requests调用 四、相关参数说明: 总结 前言 本地部署了大模型,下一步任务便是如何调用的问题,…...

20240708 每日AI必读资讯
🤖破解ChatGPT惊人耗电!DeepMind新算法训练提效13倍,能耗暴降10倍 - 谷歌DeepMind研究团队提出了一种加快AI训练的新方法——多模态对比学习与联合示例选择(JEST),大大减少了所需的计算资源和时间。 - JE…...
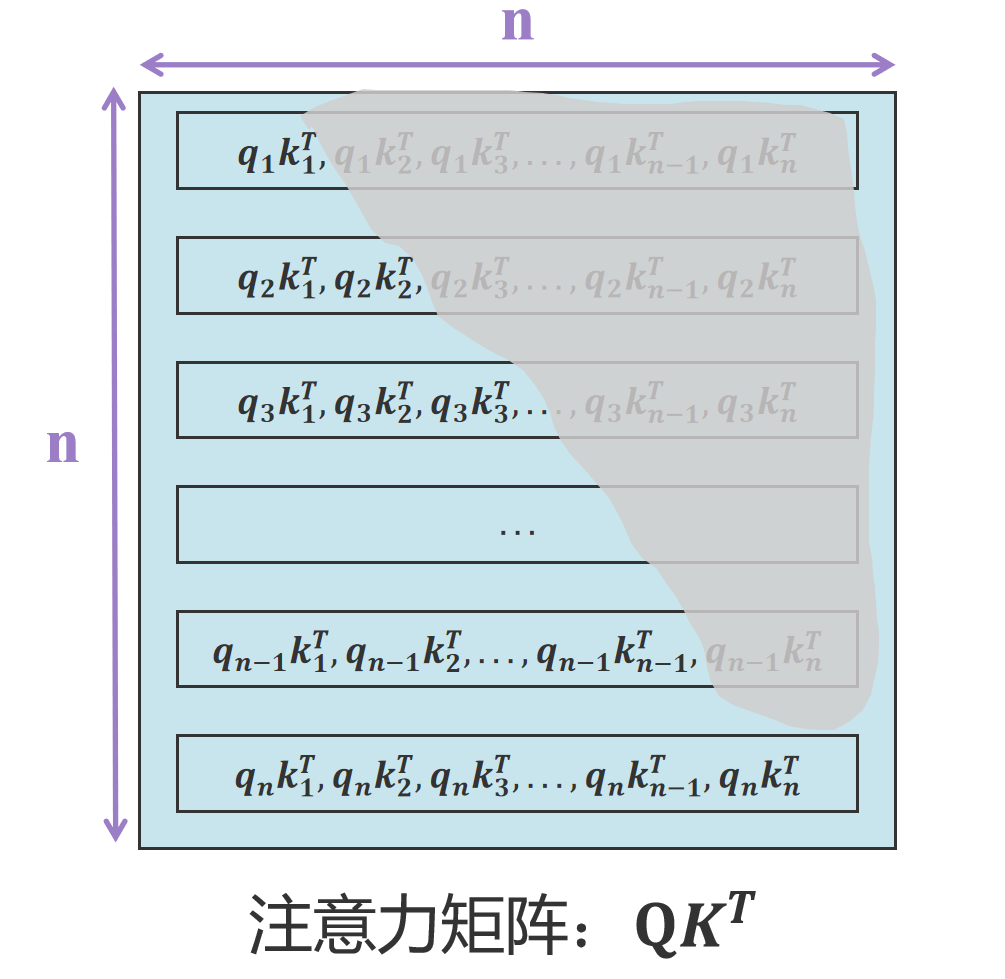
为什么KV Cache只需缓存K矩阵和V矩阵,无需缓存Q矩阵?
大家都知道大模型是通过语言序列预测下一个词的概率。假定{ x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3,…, x n − 1 x_{n-1} xn−1}为已知序列,其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x…...

VS code修改底部的行号的状态栏颜色
VSCode截图 相信很多小伙伴被底部的蓝色状态栏困扰很久了 处理的方式有两种: 1、隐藏状态栏 2、修改其背景颜色 第一种方法大伙都会,今天就使用第二种方法。 1、点击齿轮进入setting 2、我现在用的新版本,设置不是以前那种json格式展示&…...

【鸿蒙学习笔记】MVVM模式
官方文档:MVVM模式 [Q&A] 什么是MVVM ArkUI采取MVVM Model View ViewModel模式。 Model层:存储数据和相关逻辑的模型。View层:在ArkUI中通常是Component装饰组件渲染的UI。ViewModel层:在ArkUI中,ViewModel是…...

端、边、云三级算力网络
目录 端、边、云三级算力网络 NPU Arm架构 OpenStack kubernetes k3s轻量级Kubernetes kubernetes和docker区别 DCI(Data Center Interconnect) SD/WAN TF 端、边、云三级算力网络 算力网络从传统云网融合的角度出发,结合 边缘计算、网络云化以及智能控制的优势,通…...

java —— JSP 技术
一、JSP (一)前言 1、.jsp 与 .html 一样属于前端内容,创建在 WebContent 之下; 2、嵌套的 java 语句放置在<% %>里面; 3、嵌套 java 语句的三种语法: ① 脚本:<% java 代码 %>…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
