利用git reflog 命令来查看历史提交记录,并使用提交记录恢复已经被删除掉的分支
一.问题描述
当我们在操作中手误删除了某个分支,那该分支中提交的内容也没有了,我们可以利用git reflog这个命令来查看历史提交的记录从而恢复被删除的分支和提交的内容
二.模拟问题
1.创建git仓库,并提交一个文件
[root@centos7-temp /data]# git init
已初始化空的 Git 仓库于 /data/.git/[root@centos7-temp /data]# vim test.txt[root@centos7-temp /data]# cat test.txt
11111
[root@centos7-temp /data]# git add test.txt[root@centos7-temp /data]# git commit -m "first commit"
[master(根提交) af8a35f] first commit1 file changed, 1 insertion(+)create mode 100644 test.txt2.再次编辑test.txt文件并提交
[root@centos7-temp /data]# vim test.txt [root@centos7-temp /data]# cat test.txt
11111
22222[root@centos7-temp /data]# git add test.txt [root@centos7-temp /data]# git commit -m "second commit"
[master 9f10533] second commit1 file changed, 1 insertion(+)3.查看当前所处分支和提交记录
#可以看到所处分支是在master分支,在master分支中有两条提交记录
[root@centos7-temp /data]# git branch
* master[root@centos7-temp /data]# git log
commit 9f105338768642dd9306f4e0d83897847894176a (HEAD -> master)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:55:48 2023 +0800second commitcommit af8a35fd2647b15059297c4d18d18de89f14601b
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:52:58 2023 +0800first commit
4.创建并切换至新分支
[root@centos7-temp /data]# git checkout -b main
切换到一个新分支 'main'5.查看当前所处分支
[root@centos7-temp /data]# git branch
* mainmaster
6.在main分支上继续编辑test.txt文件并提交
[root@centos7-temp /data]# vim test.txt [root@centos7-temp /data]# cat test.txt
11111
22222
33333[root@centos7-temp /data]# git add test.txt [root@centos7-temp /data]# git commit -m "third commit"
[main 14cc0a8] third commit1 file changed, 1 insertion(+)7.查看提交记录
[root@centos7-temp /data]# git log
commit 14cc0a8bc11ddb183d15241858108da85507d13c (HEAD -> main)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 15:06:10 2023 +0800third commitcommit 9f105338768642dd9306f4e0d83897847894176a (master)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:55:48 2023 +0800second commitcommit af8a35fd2647b15059297c4d18d18de89f14601b
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:52:58 2023 +0800first commit
8.切换到master分支下,然后删除main分支
[root@centos7-temp /data]# git checkout master
切换到分支 'master'[root@centos7-temp /data]# git branch -D main
已删除分支 main(曾为 14cc0a8)。
9.查看所有分支,验证下main分支是否真的被删除了
[root@centos7-temp /data]# git branch
* master10.查看提交记录
#分支因为没有合并到master分支,就被删除了。所以此时master分支没有main分支上做的新的修改记录
[root@centos7-temp /data]# git log
commit 9f105338768642dd9306f4e0d83897847894176a (HEAD -> master)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:55:48 2023 +0800second commitcommit af8a35fd2647b15059297c4d18d18de89f14601b
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:52:58 2023 +0800first commit三.恢复main分支
1.查看所有分支的操作记录,对比之前在main分支查看的提交记录
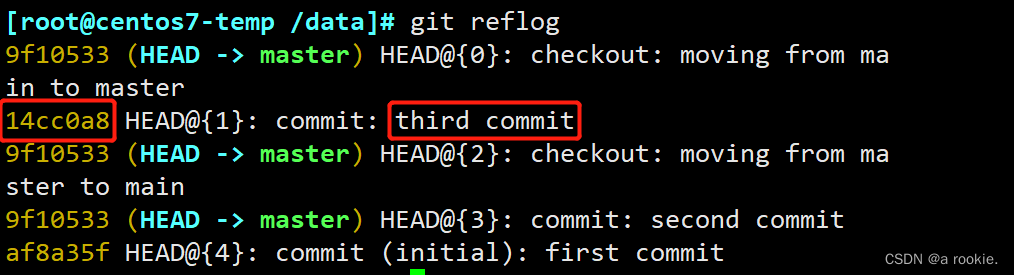
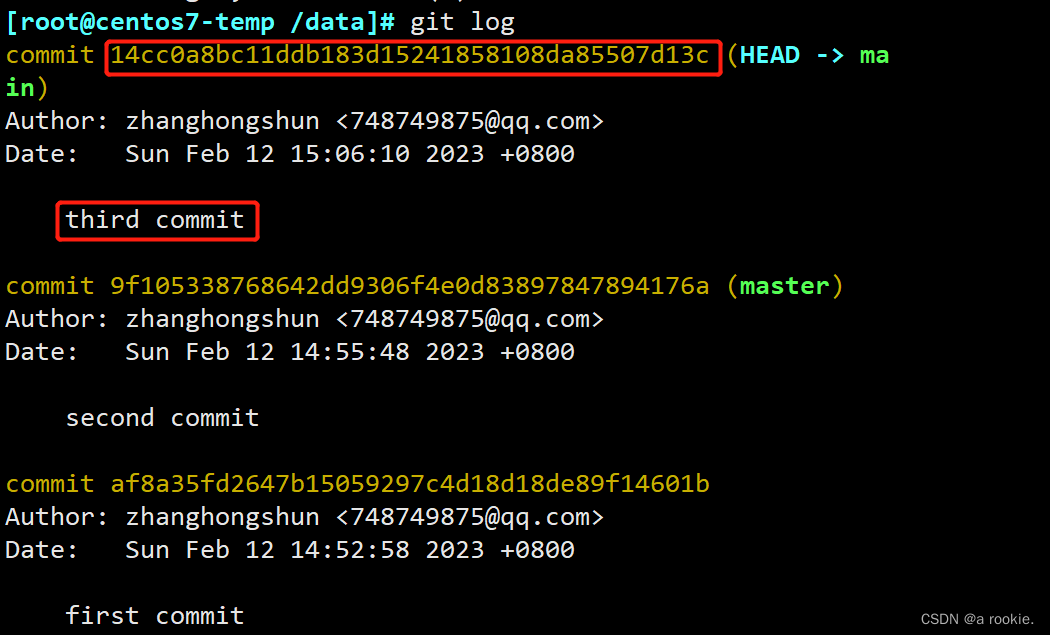
2.根据main的最后一次提交记录来恢复main分支
[root@centos7-temp /data]# git checkout -b main 14cc0a8
切换到一个新分支 'main'[root@centos7-temp /data]# git branch
* mainmaster[root@centos7-temp /data]# git log
commit 14cc0a8bc11ddb183d15241858108da85507d13c (HEAD -> main)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 15:06:10 2023 +0800third commitcommit 9f105338768642dd9306f4e0d83897847894176a (master)
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:55:48 2023 +0800second commitcommit af8a35fd2647b15059297c4d18d18de89f14601b
Author: zhanghongshun <748749875@qq.com>
Date: Sun Feb 12 14:52:58 2023 +0800first commit相关文章:

利用git reflog 命令来查看历史提交记录,并使用提交记录恢复已经被删除掉的分支
一.问题描述 当我们在操作中手误删除了某个分支,那该分支中提交的内容也没有了,我们可以利用git reflog这个命令来查看历史提交的记录从而恢复被删除的分支和提交的内容 二.模拟问题 1.创建git仓库,并提交一个文件 [rootcentos7-temp /da…...
【软件测试】大厂测试开发你真的了解吗?测试开发养成记......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 在一些大公司里&…...

Redis中的hash结构和扩容机制
1.rehash原理 hash包含两个数据结构为字典数组ht[0]和ht[1]。其中ht[0]用来存放数据,ht[1]在rehash时使用。 扩容时,ht[1]的大小为第一个大于等于ht[0].used*2的2的幂次方的数; 收缩时,ht[1]的大小为第一个大于等于ht[0].used的…...
【2023.02.08】)
【C++奇技淫巧】前置自增与后置自增的区别(++i,i++)【2023.02.08】
简介 先说i和i的区别,判断语句中if(i)是拿i的值先判断,而后自增;if(i)是先自增i再进行判断。涉及到左值与右值也有点区别,i返回的是右值,i返回的是左值。也就是下面的代码要解释的东西。 #include <iostream>i…...
实战打靶集锦-005-HL
**写在前面:**记录一次曲折的打靶经历。 目录1. 主机发现2. 端口扫描3. 服务枚举4. 服务探查4.1 浏览器访问4.2 目录枚举4.3 探查admin4.4 探查index4.5 探查login5 公共EXP搜索6. 再次目录枚举6.1 探查superadmin.php6.2 查看页面源代码6.3 base64绕过6.4 构建反弹…...
)
铁路系统各专业介绍(车机工电辆)
目录 1 车务段 1.1 职能简介 1.2 路段名单 1.3 岗位级别 2 机务段 2.1 职能简介 2.2 路段名单 2.3 岗位级别 3 工务段 3.1 职能简介 3.2 路段名单 3.3 岗位级别 4 电务段 4.1 职能简介 4.2 路段名单 4.3 岗位级别 5 车辆段 5.1 职能简介 5.2 路段名单 5.3 …...

2/11考试总结
时间安排 7:30–7:50 读题,T1貌似是个 dp ,T2 数据结构,T3 可能是数据结构。 7:50–9:45 T1,点规模非常大,可以达到 1e18 级别,感觉应该没法直接做,考虑每条新增的边的贡献,想到用 …...

Java Set集合
7 Set集合 7.1 Set集合的概述和特点 Set集合的特点 不包含重复元素的集合没有带索引的方法,所以不能使用普通for循环 Set集合是接口通过实现类实例化(多态的形式) HashSet:添加的元素是无序,不重复,无索引…...
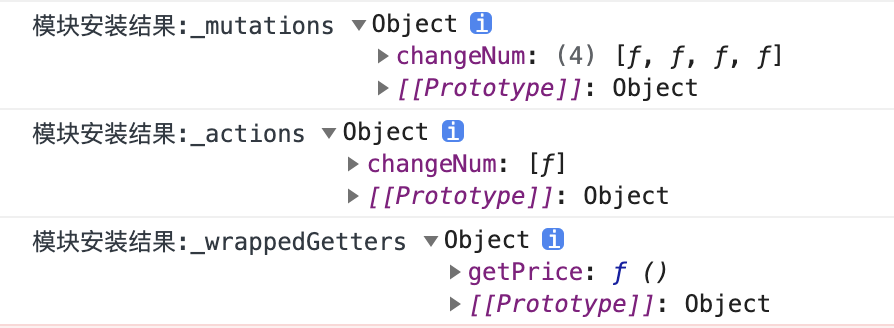
【手写 Vuex 源码】第七篇 - Vuex 的模块安装
一,前言 上一篇,主要介绍了 Vuex 模块收集的实现,主要涉及以下几个点: Vuex 模块的概念;Vuex 模块和命名空间的使用;Vuex 模块收集的实现-构建“模块树”; 本篇,继续介绍 Vuex 模…...
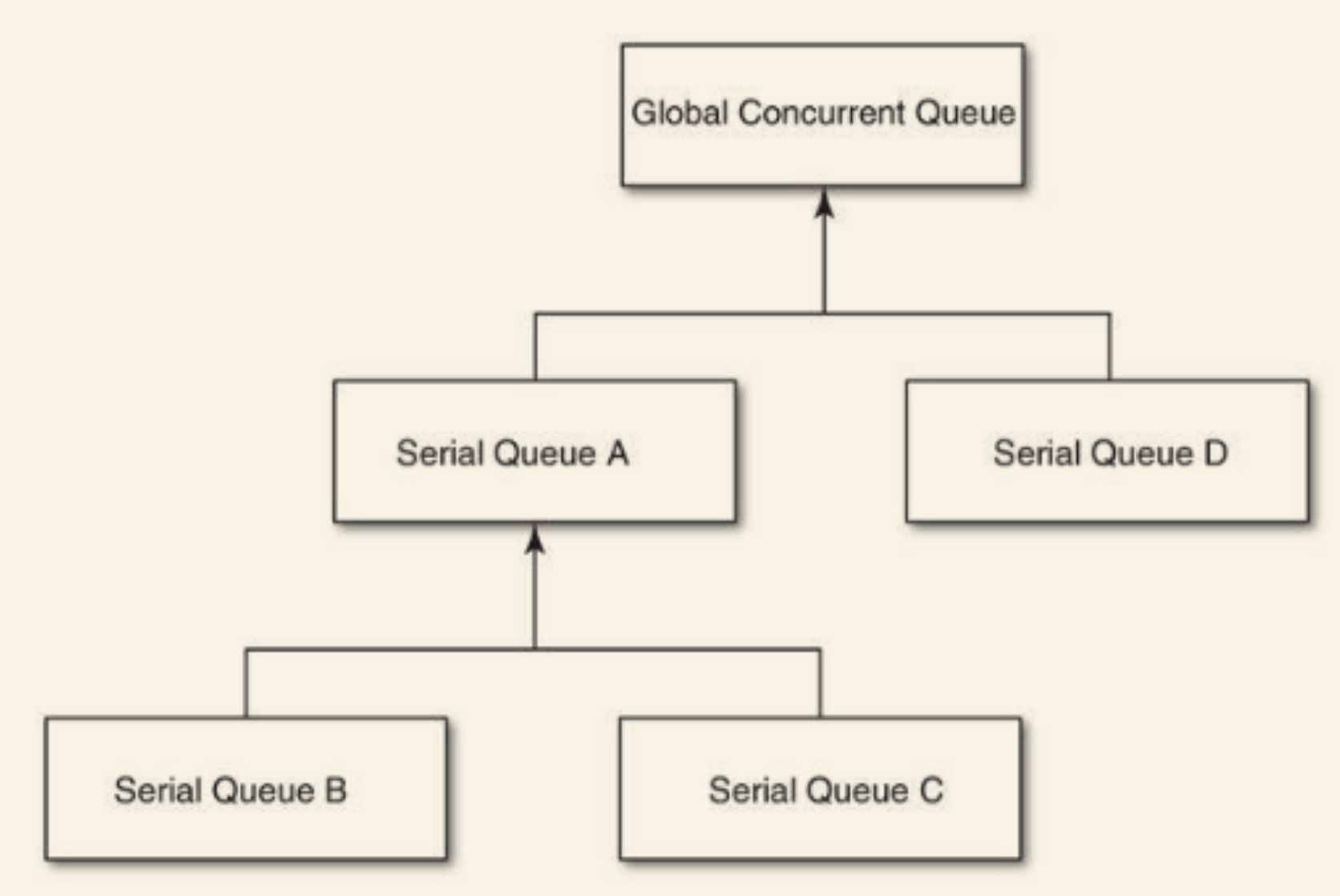
EOC第六章《块与中枢派发》
文章目录第37条:理解block这一概念第38条:为常用的块类型创建typedef第39条:用handler块降低代码分散程度第41条:多用派发队列,少用同步锁方案一:使用串行同步队列来将读写操作都安排到同一个队列里&#x…...
八、Git远程仓库操作——跨团队成员的协作
前言 前面一篇博文介绍了git团队成员之间的协作,现在在介绍下如果是跨团队成员的话,如何协作? 跨团队成员协作,其实就是你不属于那个项目的成员,你没有权限向那个仓库提交代码。但是github还有另一种 pull request&a…...

算法刷题打卡第88天:字母板上的路径
字母板上的路径 难度:中等 我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board ["abcde", "fghij", "klmno", "pqrst", "uvwxy", "…...

UVa The Morning after Halloween 万圣节后的早晨 双向BFS
题目链接:The Morning after Halloween 题目描述: 给定一个二维矩阵,图中有障碍物和字母,你需要把小写字母移动到对应的大写字母位置,不同的小写字母可以同时移动(上下左右四个方向或者保持不动 ࿰…...
)
Connext DDS属性配置参考大全(3)
Transport传输dds.participant.logging.time_based_logging.process_received_messagedds.participant.logging.time_based_logging.process_received_message.timeout...
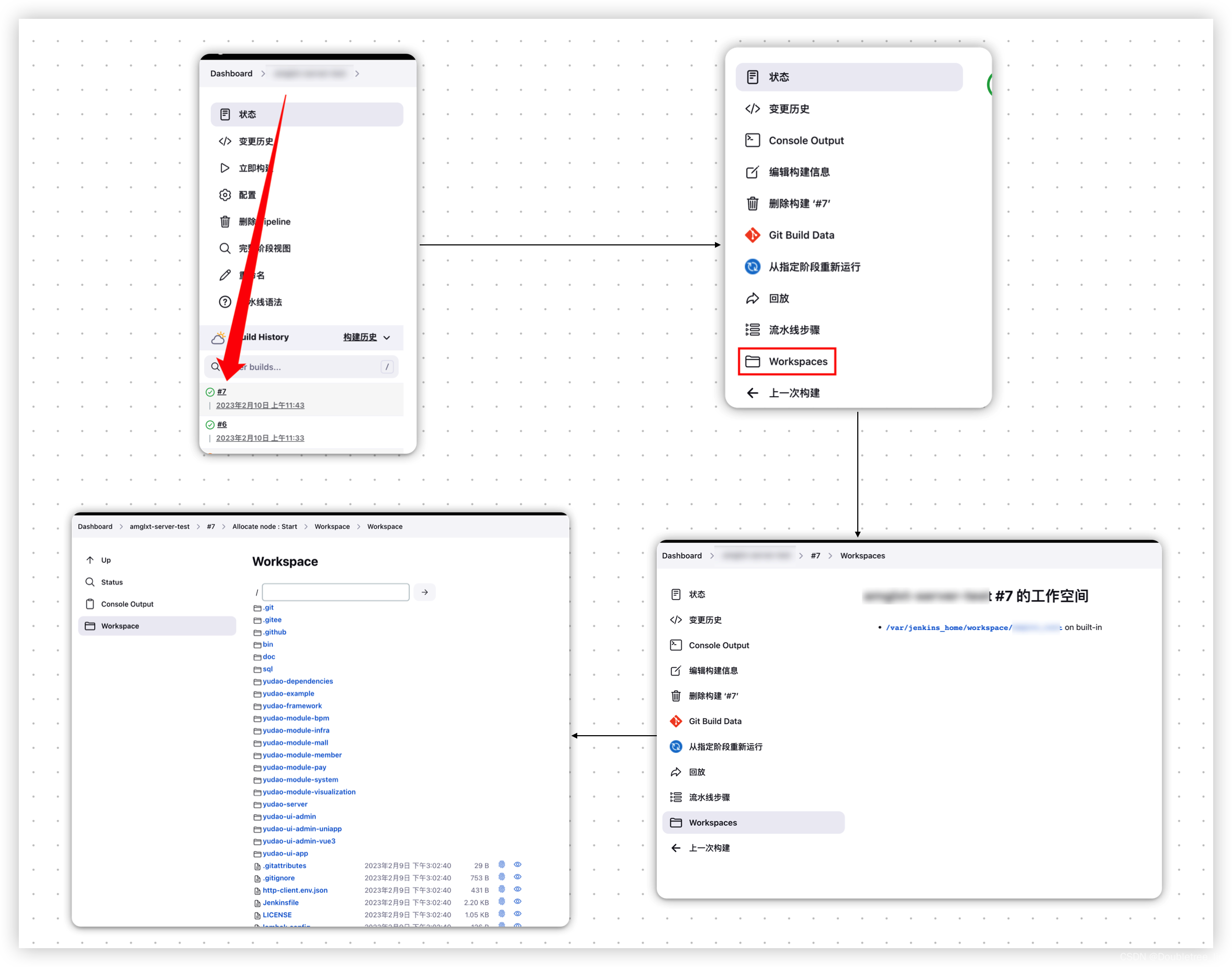
Docker-安装Jenkins-使用jenkins发版Java项目
文章目录0.前言环境背景1.操作流程1.1前期准备工作1.1.1环境变量的配置1.2使用流水线的方式进行发版1.2.1新建流水线任务1.2.2流水线操作工具tools步骤stages步骤1:拉取代码编译步骤2:发送文件并启动0.前言 学海无涯,旅“途”漫漫,“途”中小记ÿ…...

spring 中的 Bean 是否线程安全
文章目录结论1、spring中的Bean从哪里来?2、spring中什么样的Bean存在线程安全问题?3、如何处理spring Bean的线程安全问题?结论 其实,Spring 中的 Bean 是否线程安全,其实跟 Spring 容器本身无关。Spring框架中没有提…...
微电网两阶段鲁棒优化经济调度方法[3]【升级优化版本】(Matlab代码实现)
💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑…...

C++入门教程||C++ 数据类型||C++ 变量类型
C 数据类型 使用编程语言进行编程时,需要用到各种变量来存储各种信息。变量保留的是它所存储的值的内存位置。这意味着,当您创建一个变量时,就会在内存中保留一些空间。 您可能需要存储各种数据类型(比如字符型、宽字符型、整型…...
【visio使用技巧】图片导出pdf时去掉多余空白
问题 在visio导出pdf格式的图片时,往往会存在多余的白边,如下图所示: 解决方法 依次点击:菜单栏→文件→选项→自定义功能区→勾选“开发工具”→确定。 依次点击菜单栏→开发工具→显示ShapeSheet→页→Print Properties→将…...

Rust语言之Option枚举类型
概述 Option是Rust语言设计中最重要的枚举类型之一,它编码了其它语言中空值与非空值的概念,差异在于,Rust不会允许你像其它语言一样以非空值的方式来使用一个空值,这避免了很多错误。Option在标准库中的定义如下: pu…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
