【每日一题Day115】LC2335装满杯子需要的最短总时长 | 贪心
装满杯子需要的最短总时长【LC2335】
You have a water dispenser that can dispense cold, warm, and hot water. Every second, you can either fill up
2cups with different types of water, or1cup of any type of water.You are given a 0-indexed integer array
amountof length3whereamount[0],amount[1], andamount[2]denote the number of cold, warm, and hot water cups you need to fill respectively. Return the minimum number of seconds needed to fill up all the cups.
什么时候天晴呀(又在草稿里没发出来)
-
思路:如果存在两个杯子,那么每次装两杯;如果只存在一个杯子,那么每次装一杯。因此每次选择最大值和次大值进行装杯,尽可能每次装满两个杯子,减小最短时长。那么总时长取决于杯子的最大值maxmaxmax与剩下两个值的和sum−maxsum-maxsum−max的大小关系:
- 杯子的最大值大于剩下两个值的和,在装该类水杯时,可以顺便把另外两个装满,那么总时长即为杯子的最大值个数。
- 杯子的最大值小于等于剩下两个值的和,那么每次选择最大值和次大值进行装杯,那么总时长即为⌈sum/2⌉\lceil sum/2 \rceil⌈sum/2⌉。
- 局部最优:三种杯子的数量均匀减小,每次尽可能装满两个杯子
- 全局最优:装满杯子的总时长最短
-
实现
class Solution {public int fillCups(int[] amount) {int max = 0;int sum = 0;for (int num : amount){sum += num;max = Math.max(num, max);}if (max > sum - max) {return max;}else{return sum / 2 + sum % 2;}} }- 复杂度
- 时间复杂度:O(1)O(1)O(1)
- 空间复杂度:O(1)O(1)O(1)
- 复杂度
相关文章:

【每日一题Day115】LC2335装满杯子需要的最短总时长 | 贪心
装满杯子需要的最短总时长【LC2335】 You have a water dispenser that can dispense cold, warm, and hot water. Every second, you can either fill up 2 cups with different types of water, or 1 cup of any type of water. You are given a 0-indexed integer array amo…...

Flink流计算处理-旁路输出
使用Flink做流数据处理时,除了主流数据输出,还自定义侧流输出即旁路输出,以实现灵活的数据拆分。 定义旁路输出标签 首先需要定义一个OutputTag,代码如下: // 这需要是一个匿名的内部类,以便我们分析类型…...
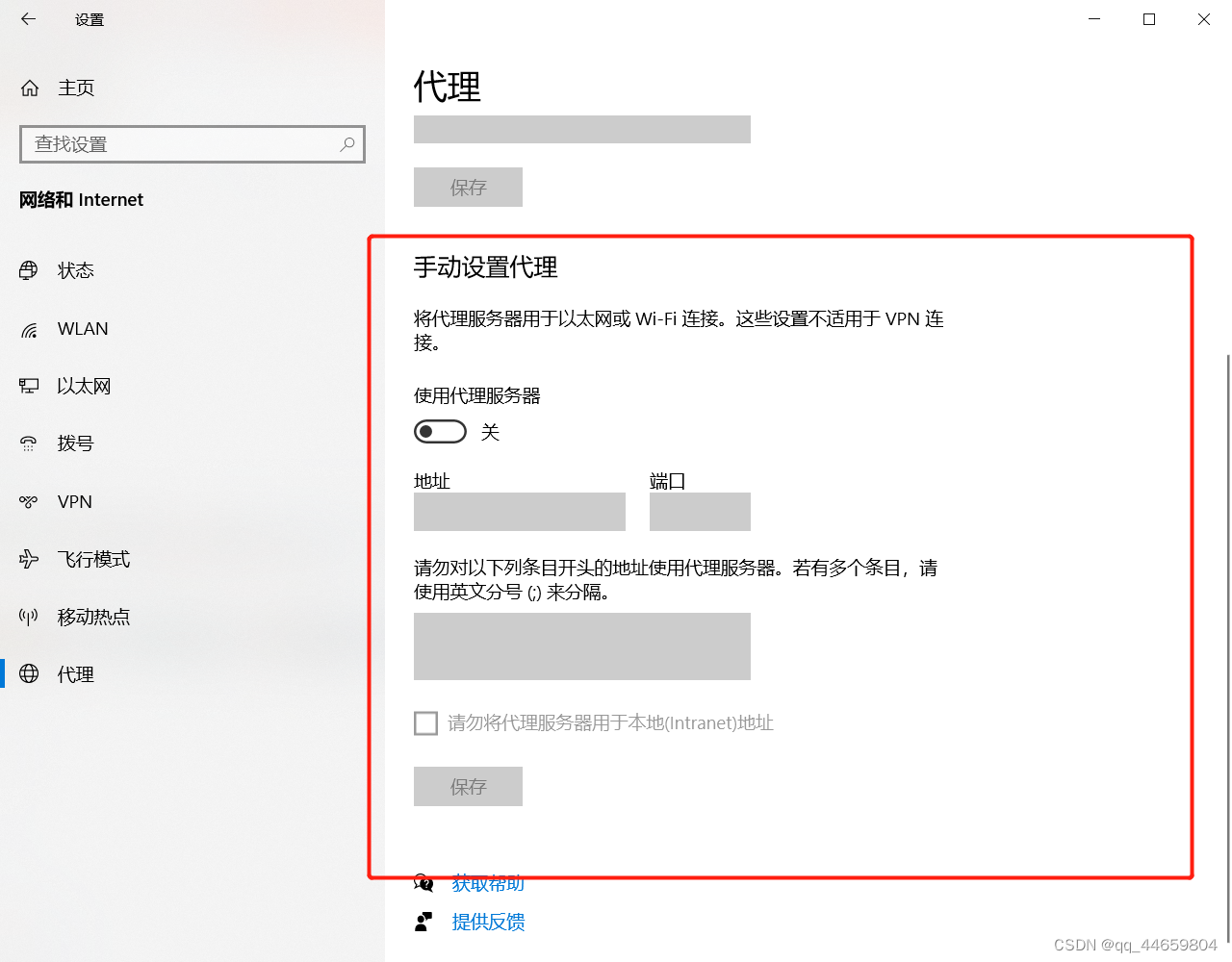
nginx正向代理的配置和使用
nginx正向代理的配置和使用 nginx正向代理的配置和使用nginx正向代理的配置和使用安装包准备下载nginx安装包下载正向代理模块的包版本与模块对照表部署nginx服务上传nginx包和正向模块包解压,改名安装nginx配置正向代理创建nginx用户检查nginx配置并启动nginx服务所在服务器验…...

Oracle Trace File Analyzer 介绍及简单使用
一、什么是Oracle Trace File Analyzer Oracle Autonomous Health Framework(AHF) 包含 Oracle ORAchk, Oracle EXAchk, and Oracle Trace File Analyzer(TFA). AHF工具包包含了Oracle常用的多种诊断工具,如 ORAchk, Oracle EXAchk, and Oracle Trace File Analyzer…...
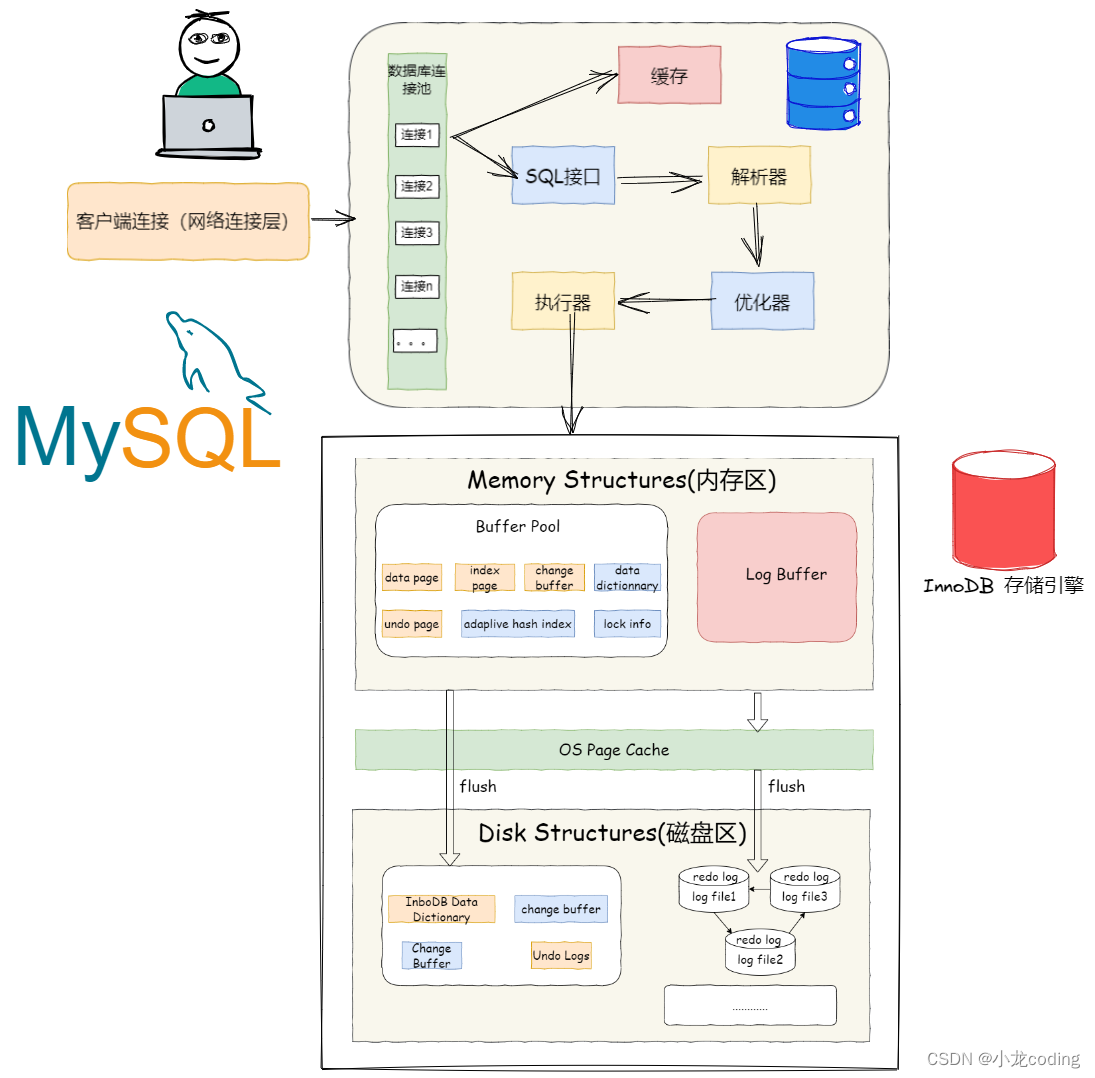
面试实战篇 | 快手本地生活,结合项目谈Redis实战项目场景?MySQL InnoDB存储引擎如何工作的?策略模式?
本期是【你好,面试官】系列文章的第21期,持续更新中…。 《你好,面试官》系列目前已经连载20篇了,据说看了这个系列的朋友都拿到了大厂offer~ 你好,面试官 | 你真的理解面向 “对象”?你好,面…...
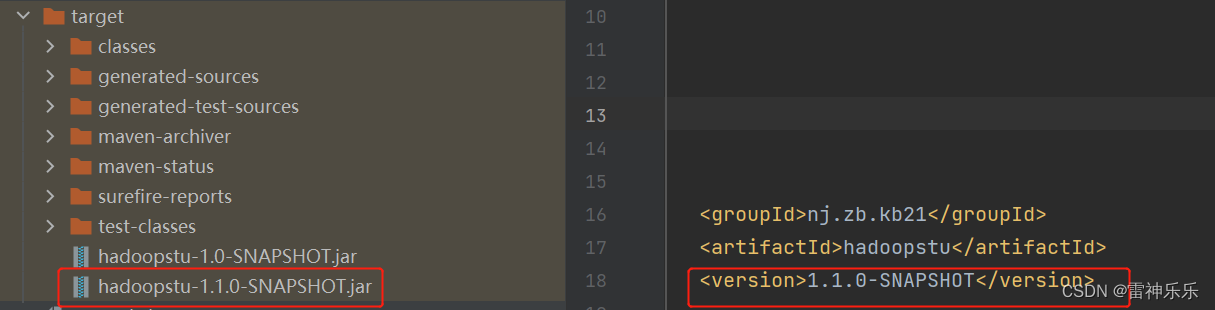
Hadoop之——WordCount案例与执行本地jar包
目录 一、WordCount代码 (一)WordCount简介 1.wordcount.txt (二)WordCount的java代码 1.WordCountMapper 2.WordCountReduce 3.WordCountDriver (三)IDEA运行结果 (四)Hadoop运行wordcount 1.在HDFS上新建一个文件目录 2.新建一个文件,并上传至该目录下…...
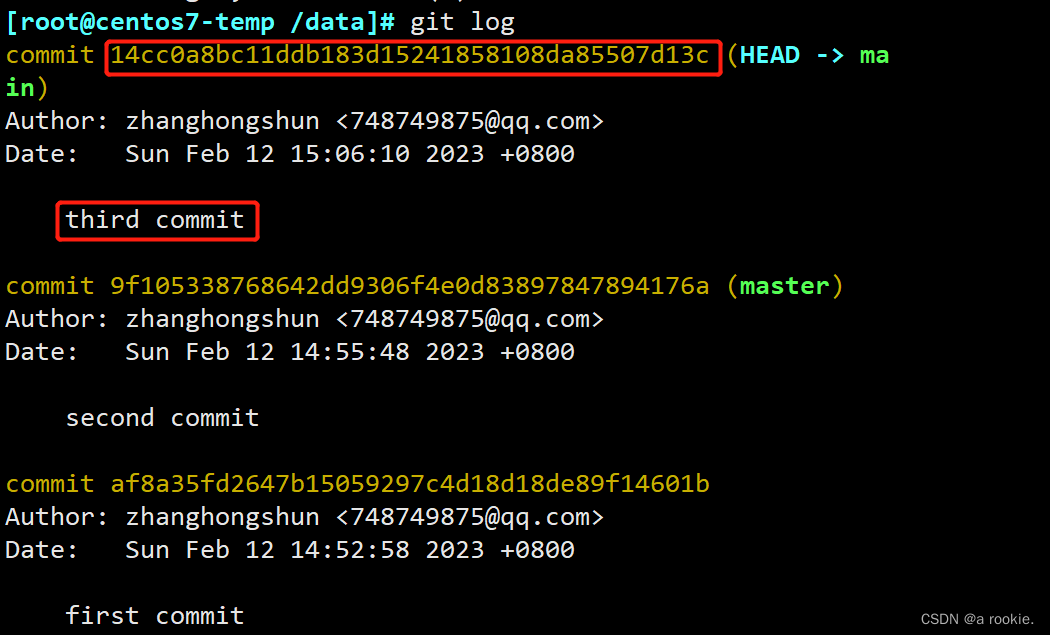
利用git reflog 命令来查看历史提交记录,并使用提交记录恢复已经被删除掉的分支
一.问题描述 当我们在操作中手误删除了某个分支,那该分支中提交的内容也没有了,我们可以利用git reflog这个命令来查看历史提交的记录从而恢复被删除的分支和提交的内容 二.模拟问题 1.创建git仓库,并提交一个文件 [rootcentos7-temp /da…...
【软件测试】大厂测试开发你真的了解吗?测试开发养成记......
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 在一些大公司里&…...

Redis中的hash结构和扩容机制
1.rehash原理 hash包含两个数据结构为字典数组ht[0]和ht[1]。其中ht[0]用来存放数据,ht[1]在rehash时使用。 扩容时,ht[1]的大小为第一个大于等于ht[0].used*2的2的幂次方的数; 收缩时,ht[1]的大小为第一个大于等于ht[0].used的…...
【2023.02.08】)
【C++奇技淫巧】前置自增与后置自增的区别(++i,i++)【2023.02.08】
简介 先说i和i的区别,判断语句中if(i)是拿i的值先判断,而后自增;if(i)是先自增i再进行判断。涉及到左值与右值也有点区别,i返回的是右值,i返回的是左值。也就是下面的代码要解释的东西。 #include <iostream>i…...
实战打靶集锦-005-HL
**写在前面:**记录一次曲折的打靶经历。 目录1. 主机发现2. 端口扫描3. 服务枚举4. 服务探查4.1 浏览器访问4.2 目录枚举4.3 探查admin4.4 探查index4.5 探查login5 公共EXP搜索6. 再次目录枚举6.1 探查superadmin.php6.2 查看页面源代码6.3 base64绕过6.4 构建反弹…...
)
铁路系统各专业介绍(车机工电辆)
目录 1 车务段 1.1 职能简介 1.2 路段名单 1.3 岗位级别 2 机务段 2.1 职能简介 2.2 路段名单 2.3 岗位级别 3 工务段 3.1 职能简介 3.2 路段名单 3.3 岗位级别 4 电务段 4.1 职能简介 4.2 路段名单 4.3 岗位级别 5 车辆段 5.1 职能简介 5.2 路段名单 5.3 …...

2/11考试总结
时间安排 7:30–7:50 读题,T1貌似是个 dp ,T2 数据结构,T3 可能是数据结构。 7:50–9:45 T1,点规模非常大,可以达到 1e18 级别,感觉应该没法直接做,考虑每条新增的边的贡献,想到用 …...

Java Set集合
7 Set集合 7.1 Set集合的概述和特点 Set集合的特点 不包含重复元素的集合没有带索引的方法,所以不能使用普通for循环 Set集合是接口通过实现类实例化(多态的形式) HashSet:添加的元素是无序,不重复,无索引…...
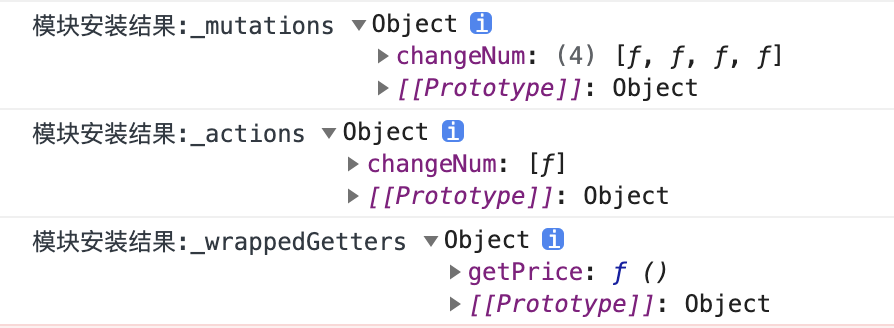
【手写 Vuex 源码】第七篇 - Vuex 的模块安装
一,前言 上一篇,主要介绍了 Vuex 模块收集的实现,主要涉及以下几个点: Vuex 模块的概念;Vuex 模块和命名空间的使用;Vuex 模块收集的实现-构建“模块树”; 本篇,继续介绍 Vuex 模…...
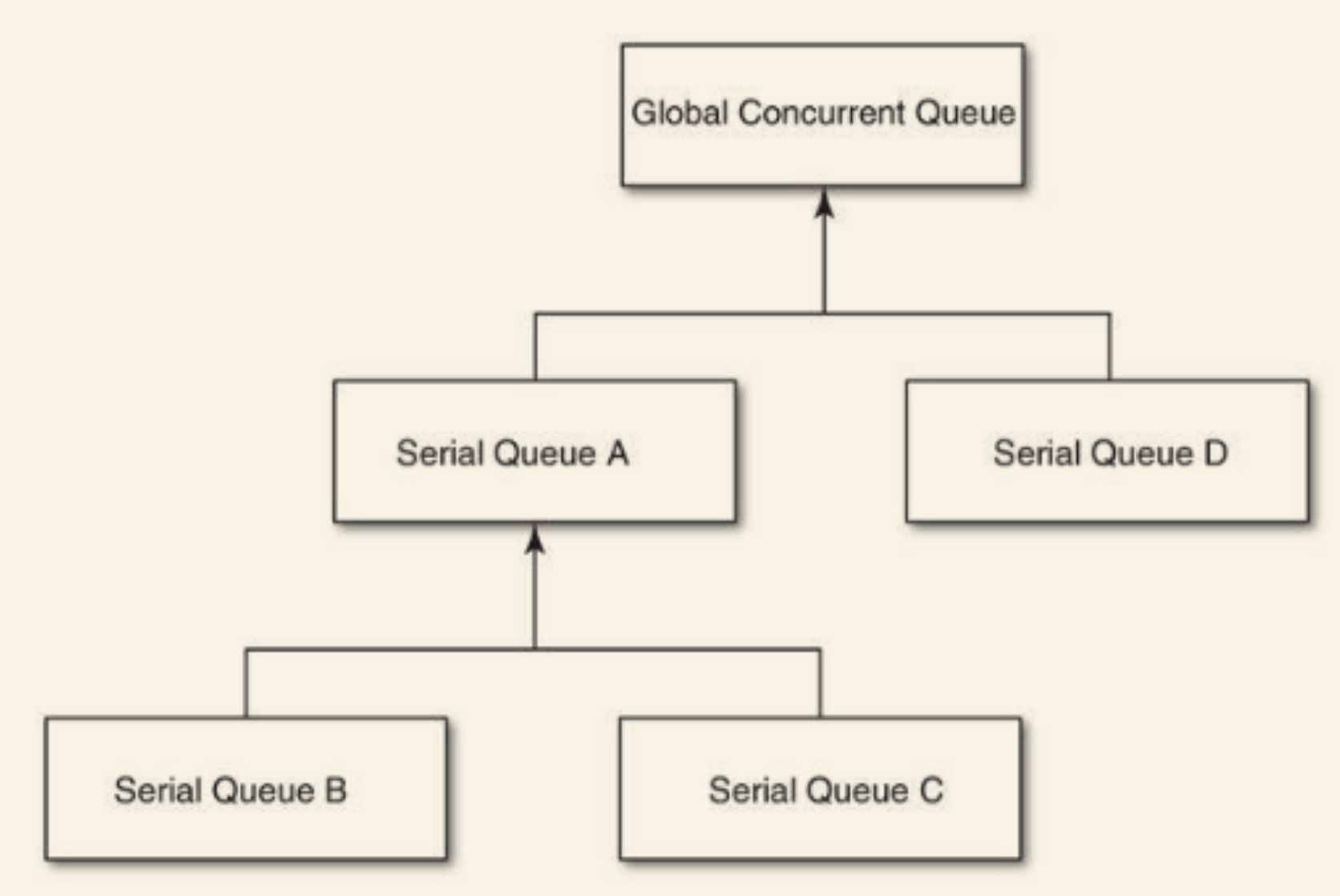
EOC第六章《块与中枢派发》
文章目录第37条:理解block这一概念第38条:为常用的块类型创建typedef第39条:用handler块降低代码分散程度第41条:多用派发队列,少用同步锁方案一:使用串行同步队列来将读写操作都安排到同一个队列里&#x…...
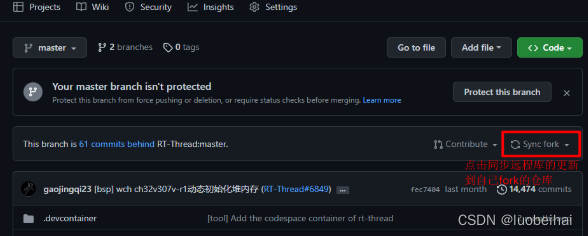
八、Git远程仓库操作——跨团队成员的协作
前言 前面一篇博文介绍了git团队成员之间的协作,现在在介绍下如果是跨团队成员的话,如何协作? 跨团队成员协作,其实就是你不属于那个项目的成员,你没有权限向那个仓库提交代码。但是github还有另一种 pull request&a…...

算法刷题打卡第88天:字母板上的路径
字母板上的路径 难度:中等 我们从一块字母板上的位置 (0, 0) 出发,该坐标对应的字符为 board[0][0]。 在本题里,字母板为board ["abcde", "fghij", "klmno", "pqrst", "uvwxy", "…...

UVa The Morning after Halloween 万圣节后的早晨 双向BFS
题目链接:The Morning after Halloween 题目描述: 给定一个二维矩阵,图中有障碍物和字母,你需要把小写字母移动到对应的大写字母位置,不同的小写字母可以同时移动(上下左右四个方向或者保持不动 ࿰…...
)
Connext DDS属性配置参考大全(3)
Transport传输dds.participant.logging.time_based_logging.process_received_messagedds.participant.logging.time_based_logging.process_received_message.timeout...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...

python学习day39
图像数据与显存 知识点回顾 1.图像数据的格式:灰度和彩色数据 2.模型的定义 3.显存占用的4种地方 a.模型参数梯度参数 b.优化器参数 c.数据批量所占显存 d.神经元输出中间状态 4.batchisize和训练的关系 import torch import torchvision import torch.nn as nn imp…...
