算法:排序
排序算法
- 1. 简单排序
- 1.1 直接插入排序
- 1.2 冒泡排序
- 1.3 简单选择排序
- 2. 希尔排序
- 3. 快速排序
- 4. 堆排序
- 5. 归并排序
将文件的内容按照某种规则进行排列。
排序算法的稳定判定:若在待排序的一个序列中, R i R_i Ri和 R j R_j Rj的关键码相同,即 k i = k j k_i=k_j ki=kj,且在排序前 R i R_i Ri领先于 R j R_j Rj,那么当排序后,如果 R i R_i Ri和 R j R_j Rj的相对次序保持不变, R i R_i Ri仍领先于 R j R_j Rj,则称此类排序方法为稳定的。若可能出现 R j R_j Rj领先于 R i R_i Ri的情况,则称此列排序是不稳定的。
排序可分为内部排序和外部排序,通过是否全部在内存中排序进行判定。
排序完成两个操作:
- 比较两个关键码的大小;
- 将记录从一个位置移动到另一个为止。
1. 简单排序
1.1 直接插入排序
将某个数据插入已经排好的队列中。
void insertSort(int data[], int n)
{int i, j;int temp;for (i = 1; i < n; i++){if (data[i] < data[i - 1]) {temp = data[i]; data[i] = data[i - 1];for (j = i - 2; j >= 0 && data[j] > temp; j--) data[j + 1] = data[j];data[j+1] = temp;}}
}
运行结果:
int array[8] = {12, 18184, 45, 78, 45, 555, 47, 36};insertSort(array, 8);for (int i = 0; i < 8; i++)
{printf("%d\n", array[i]);
}

直接插入排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。排序过程中仅需要一个元素的辅助空间,空间复杂度为 O ( 1 ) O(1) O(1)。直接插入排序是一种稳定的排序方法。
1.2 冒泡排序
顾名思义,冒泡法就是像气泡上浮一样把数据逐渐传递上去。
void bubbleSort(int data[], int n)
{int i, j, tag = 1; //tag表示排序过程中是否交换过元素值int temp;for (i = 1; tag && i < n; i++){tag = 0;for (j = 0; j < n - i; j++){if (data[j]>data[j+1]){temp = data[j];data[j] = data[j+1];data[j + 1] = temp;tag = 1;}}}
}
int array[8] = {12, 18184, 45, 78, 45, 555, 47, 36};
//insertSort(array, 8);
bubbleSort(array, 8);for (int i = 0; i < 8; i++)
{printf("%d\n", array[i]);
}

冒泡排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。排序过程中仅需要一个元素的辅助空间,空间复杂度为 O ( 1 ) O(1) O(1)。冒泡排序是一种稳定的排序方法。
1.3 简单选择排序
逐步找出最小的元素,依次放置。
void selectSort(int data[], int n)
{int i, j, k;int temp;for (i = 0; i < n-1; i++){k = i;for ( j = i+1; j < n; j++){if (data[j] < data[k]) k = j;}if (k!=i){temp = data[i];data[i] = data[k];data[k] = temp;}}
}
算法结果:
int array[8] = {12, 18184, 45, 78, 45, 555, 47, 36};//insertSort(array, 8);
//bubbleSort(array, 8);
selectSort(array, 8);for (int i = 0; i < 8; i++)
{printf("%d\n", array[i]);
}

简单选择排序的时间复杂度为 O ( n 2 ) O(n^2) O(n2)。排序过程中仅需要一个元素的辅助空间,空间复杂度为 O ( 1 ) O(1) O(1)。简单选择排序是一种不稳定的排序方法。
2. 希尔排序
希尔排序又称为“缩小增量排序”,是对直接插入排序方法的改进。
希尔排序的基本思想是:先将整个待排记录序列分割成若干子序列,然后分别进行直接插入排序,待整个序列中的记录基本有序时,再对全体记录进行一次直接插入排序。具体做法是先取一个小于n的整数 d 1 d_1 d1作为第一个增量,将所有相距为 d 1 d_1 d1的记录放在同一个组中,从而把文件的全部记录分成 d 1 d_1 d1组,在各组内进行直接插入排序;然后取第二个增量 d 2 ( d 2 < d 1 ) d_2(d_2<d_1) d2(d2<d1),重复上述分组和排序工作,依此类推,直至所取的增量 d i = 1 ( d i < d i − 1 < . . . < d 2 < d 1 ) d_i=1(d_i<d_{i-1}<...<d_2<d_1) di=1(di<di−1<...<d2<d1),即所有记录放在同一组进行直接插入排序,将所有记录排列有序为止。

/*************************************************Function:shellSort,希尔排序方法Description: 整数序列排序,从小到大Input: data[] 排序数组n 数组大小delta[] 长度为m且递减有序的增量序列最后一个元素为1m delta[]数组大小Output:输出转换结果Return: 0
*************************************************/
void shellSort(int data[], int n, int delta[], int m)
{int k, i, dk, j; int temp;for ( i = 0; i < m; i++){dk = delta[i];for (k = dk; k < n; ++k){if (data[k]<data[k-dk]){temp = data[k];for (j = k - dk; j>0&&temp<data[j]; j-=dk){data[j + dk] = data[j];}data[j + dk] = temp;}}}
}
希尔排序的时间复杂度为 O ( N 1.3 ) O(N^{1.3}) O(N1.3).希尔排序是不稳定的排序方法。
3. 快速排序
快速排序
一趟快速排序的过程称为一次划分,具体做法是:附设两个元素位置指示变量 i i i和 j j j,它们的初值分别指向待排序列的第一个记录和最后一个记录。设枢轴记录(通常是第一个记录)的关键码为 pivot,则首先从j所给位置起向前搜索,找到第一个关键码小于 pivot 的记录时停止,然后从i所给位置起向后搜索,找到第一个关键码大于pivot 的记录时停止,此时交换j所给位置和i所给位置的元素,重复该过程直至i与i相等为止,完成一趟划分。
//用data[low]的值作为枢轴元素pivot进行划分
//不断劈成两半之后排序
int partition(int data[], int low, int high)
{int i, j;int pivot;while (i<j){while (i<j&&data[j]>=pivot){j--;}data[i] = data[j];while (i < j && data[i] <= pivot){i++;}data[j] = data[i];}data[i] = pivot;return i;
}/*************************************************Function:quickSort,快速排序方法Description: 整数序列排序,从小到大Input: data[] 排序数组low 数组最低位high 数组最高位Output:输出转换结果Return: 0
*************************************************/
void quickSort(int data[], int low, int high)
{if (low < high){int loc = partition(data, low, high);quickSort(data,low,loc-1);quickSort(data, loc + 1, high);}
}
4. 堆排序
5. 归并排序
相关文章:

算法:排序
排序算法 1. 简单排序1.1 直接插入排序1.2 冒泡排序1.3 简单选择排序 2. 希尔排序3. 快速排序4. 堆排序5. 归并排序 将文件的内容按照某种规则进行排列。 排序算法的稳定判定:若在待排序的一个序列中, R i R_i Ri和 R j R_j Rj的关键码相同…...

MyBatis-Plus 更新对象时如何将字段值更新为 null
MyBatis-Plus 是一个 MyBatis 的增强工具,在简化开发、提高效率方面表现非常出色。然而,在使用 MyBatis-Plus 更新对象时,默认情况下是不会将字段值更新为 null 的。这是因为 MyBatis-Plus 使用了非空字段策略(FieldStrategy&…...

Unreal5从入门到精通之如何在VR中使用3DUI
文章目录 前言创建3DUI1.新建控件蓝图2.添加控件到画布上3.新建Actor蓝图MyUIActor4.添加控件组件Widget5.设置控件类和画布大小6.创建MyUIActor实例到场景中3DUI和VR射线交互1.添加按钮的点击事件2.设置MyUIActor碰撞响应3.VRPawn添加控件交互组件4.添加手柄Trigger点击事件绑…...

ViSual studio如何安装 并使用GeographicLib
在C的 Boost.Geometry、GDAL/OGR 和 GeographicLib。这些库都可以用于计算两个经纬度点之间的地面距离。 . Boost.Geometry 描述:Boost库的一部分,提供了几何计算功能,包括计算两点之间的地面距离。 优势:轻量级、易于集成到C项…...
——分布式缓存 Ehcache 整合)
Java程序设计:spring boot(11)——分布式缓存 Ehcache 整合
目录 1 Spring Cache 相关注解说明 1.1 CacheConfig 1.2 Cacheable 1.3 CachePut 1.4 CacheEvict 1.5 Caching 2 环境配置 2.1 pom.xml 依赖添加 2.2 ehcahe.xml ⽂件添加 2.3 application.yml 缓存配置 2.4 启动缓存 2.5 JavaBean 对象实现序列化 3 缓存实现 3.…...

豆包,攻克数字是个什么工具?《GKData-挖掘数据的无限可能》(数据爬虫采集工具)
豆包,攻克数字是个什么工具? “攻克数字” 指的是 “攻克数字(GKData)” 这样一款工具。是一款针对网页、APP中数据自动解析转表存入数据库的软件,为数据工作者而生。它是一个不会编程也能用的可视化数据解析为标准二…...

说一说QWidget
目录 关于QWidget 作为界面组件时,你需要有印象的 1. 控制属性 2. 组件状态与交互属性 3. 外观和样式属性 4. 布局与子组件管理属性 5. 图标和光标属性 6. 大小策略属性 作为单独的窗体的属性 写Qt快两年了,也写过一些规模偏大的软件,…...

Web3.0技术入门
Web3.0技术入门是一个涉及多个方面和领域的复杂过程,以下是一些关键的步骤和要点,帮助您初步了解并掌握Web3.0技术。 一、了解Web3.0的基本概念 Web3.0也被称为下一代互联网,它是对当前互联网(Web2.0)的演进和升级。…...

spygalss cdc 检测的bug(二)
当allow_qualifier_merge设置为strict的时候,sg是要检查门的极性的。 如果qualifier和src经过与门汇聚,在同另一个src1信号或门汇聚,sg是报unsync的。 假设当qualifier为0时,0&&src||src1src1,src1无法被gat…...
之 选择公理(Axiom of Choice)注解)
集合论(ZFC)之 选择公理(Axiom of Choice)注解
直观感受(Intuition) 集合论(ZFC)中的 "C" 指的是选择公理(Axiom of Choice)中的"choice"。简单来说,对于任一非空集合 S,那么存在一个函数 f,选择出…...

JS:字符串操作
目录 1、 字符串分割 1、 字符串分割 var str "123,456,789"; console.log(str.split(,)); // ["123", "456", "789"]...

.NET 一款二进制文件转换Shellcode的工具
01阅读须知 此文所提供的信息只为网络安全人员对自己所负责的网站、服务器等(包括但不限于)进行检测或维护参考,未经授权请勿利用文章中的技术资料对任何计算机系统进行入侵操作。利用此文所提供的信息而造成的直接或间接后果和损失…...

【CSS】——基础入门常见操作
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:CSS引入 二:CSS对元素进行美化 1:style修饰 2:选…...
词法分析)
LuaJIT源码分析(五)词法分析
LuaJIT源码分析(五)词法分析 lua虽然是脚本语言,但在执行时,还是先将脚本编译成字节码,然后再由虚拟机解释执行。在编译脚本时,首先需要对源代码进行词法分析,把源代码分解为token流。lua的toke…...

005 匿名信
005 匿名信 题目描述 电视剧《分界线》里面有一个片段,男主为了向警察透露案件细节,且不暴露自己,于是将报刊上的字剪下来,剪拼成一封匿名信。现在有一名举报人,希望借鉴这种方式,使用英文报刊完成举报操…...

聊聊Web3D 发展趋势
随着 Web 技术的不断演进,Web3D 正逐渐成为各行业数字化的重要方向。Web3D 是指在网页中展示 3D 内容的技术集合。近年来,由于 WebGL、WebGPU 等技术的发展,3D 内容已经能够直接在浏览器中渲染,为用户提供更加沉浸、互动的体验。以…...

【数据结构与算法】LeetCode: 贪心算法
文章目录 LeetCode: 贪心算法买卖股票的最佳时机 (Hot100)买卖股票的最佳时机 II跳跃游戏 (Hot100)跳跃游戏 II(Hot100)划分字母区间 (Hot100)分发饼干K次取反后最大化的…...

Date 日期类的实现(c++)
本文用c实现日期类 将会实现以下函数 bool operator<(const Date& d);bool operator<(const Date& d);bool operator>(const Date& d);bool operator>(const Date& d);bool operator(const Date& d);bool operator!(const Date& d);Date&…...

智能家居10G雷达感应开关模块,飞睿智能uA级别低功耗、超高灵敏度,瞬间响应快
在当今科技飞速发展的时代,智能家居已经逐渐成为人们生活中不可或缺的一部分。从智能灯光控制到智能家电的联动,每一个细节都在为我们的生活带来便利和舒适。而在众多智能家居产品中,10G 雷达感应开关模块以其独特的优势,正逐渐成…...

头歌——人工智能(机器学习 --- 决策树2)
文章目录 第5关:基尼系数代码 第6关:预剪枝与后剪枝代码 第7关:鸢尾花识别代码 第5关:基尼系数 基尼系数 在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益率…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

Java严格模式withResolverStyle解析日期错误及解决方案
在Java中使用DateTimeFormatter并启用严格模式(ResolverStyle.STRICT)时,解析日期字符串"2025-06-01"报错的根本原因是:模式字符串中的年份格式yyyy被解释为YearOfEra(纪元年份),而非…...
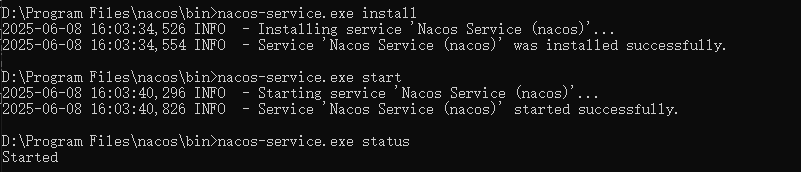
Windows开机自动启动中间件
WinSW(Windows Service Wrapper 是一个开源的 Windows 服务包装器,它可以帮助你将应用程序打包成系统服务,并实现开机自启动的功能。 一、下载 WinSW 下载 WinSW-x64.exe v2.12.0 (⬇️ 更多版本下载) 和 sample-minimal.xml 二、配置 WinS…...
