数楼梯(加强版)
数楼梯(加强版)
题目背景:
小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上.
他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题.
题目描述:
1楼到2楼楼梯有n级台阶。小明每次可以爬一格、走两格或者跨三格。问最终有几种方案到二楼?答案对998244353取模。
输入格式:
一行一个数n。
输出格式:
一行一个数,表示方案数。
输入输出样例
输入 #1:
3
输出 #1:
4
输入 #2:
5
输出 #2:
13
提示说明:
n≤1000
时间:1000ms
空间:256M
(上楼梯时不能往回走)
如果觉得这道题太难可以前往P1255先做数楼梯简单版:
https://www.luogu.com.cn/problem/P1255
思路:
1.暴力法
很容易看出来,这是一道递归题,我们可以用暴力递归来解决。
#include<iostream>
using namespace std;
static const int mod=998244353;
long long sum=0;
int n;
long long fun(int x){if(x==n)return 1;if(x>n)return 0;long long s1=0,s2=0,s3=0;s1+=fun(x+1)%mod;s2+=fun(x+2)%mod;s3+=fun(x+3)%mod;return (s1+s2+s3)%mod;
}
int main(){cin>>n;cout<<fun(0)<<endl; return 0;
}但是这个份代码会超时,非常慢,所以要进行优化!
2.递推法
我们用 f(x) 表示爬到第 x 级台阶的方案数,考虑最后一步可能跨了一级台阶,也可能跨了两级台阶,所以我们可以列出如下式子:
f(x)=f(x−1)+f(x−2)
它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x−2 级台阶的方案数的和。很好理解,因为每次只能爬 1 级或 2 级,所以 f(x) 只能从 f(x−1)和 f(x−2) 转移过来,而这里要统计方案总数,我们就需要对这两项的贡献求和。
以上是动态规划的转移方程,下面我们来讨论边界条件。我们是从第 0 级开始爬的,所以从第 0 级爬到第 0 级我们可以看作只有一种方案,即 f(0)=1;从第 0 级到第 1 级也只有一种方案,即爬一级,f(1)=1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下,根据转移方程得到 f(2)=2,f(3)=3,f(4)=5,……,我们把这些情况都枚举出来,发现计算的结果是正确的。
我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n)的实现,但是由于这里的 f(x) 只和 f(x−1)) 与 f(x−2)有关,所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。下面的代码中给出的就是这种实现。
#include<iostream>
using namespace std;
static const int mod=998244353;
void fun(int n){long long max[1001];int i=0;max[0]=1;max[1]=2;max[2]=4;for(int j=3;j<n;j++)max[j]=(max[j-1]+max[j-2]+max[j-3])%mod;cout<<max[n-1]<<endl;
}
int main(){int n;cin>>n;fun(n); return 0;
}总结:
对于这道题,有些像斐波那契数列,需要将递归进行优化才可以解决。
题目链接:
数楼梯(加强版) - 洛谷https://www.luogu.com.cn/problem/U267577
相关文章:

数楼梯(加强版)
数楼梯(加强版) 题目背景: 小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上. 他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题. 题目描述: 1楼到2楼楼梯有n级台阶。小明每…...

MySQL-数据类型
数据类型简介数据表由多列字段构成,每一个字段指定了不同的数据类型,指定了数据类型之后,也就决定了向字段插入的数据内容。不同的数据类型也决定了 MySQL 在存储它们的时候使用的方式,以及在使用它们的时候选择什么运算符号进行运…...

剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)
剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)1. 题目2. 解题思路3. 数据类型功能函数总结4. java代码5. 踩坑记录1. 题目 从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。 例如: 给定二叉…...

C#网络爬虫开发
1前言爬虫一般都是用Python来写,生态丰富,动态语言开发速度快,调试也很方便但是我要说但是,动态语言也有其局限性,笔者作为老爬虫带师,几乎各种语言都搞过,现在这个任务并不复杂,用我…...

Fastjson 总结
0x00 前言 这一篇主要是针对已经完成的fastjson系列做一个知识点总结,一来是为了更加有条理的梳理已经存在的内容,二来是为了更好的复习和利用。 0x01 Fastjson基础知识点 1.常见问题: 问:fastjson的触发点是什么?…...

文件路径模块os.path
文件路径模块os.path 文章目录文件路径模块os.path1.概述2.解析路径2.1.拆分路径和文件名split2.2.获取文件名称basename2.3.返回路径第一部分dirname2.4.扩展名称解析路径splitext2.5.返回公共前缀路径commonprefix3.创建路径3.1.拼接路径join3.2.获取家目录3.3.规范化路径nor…...
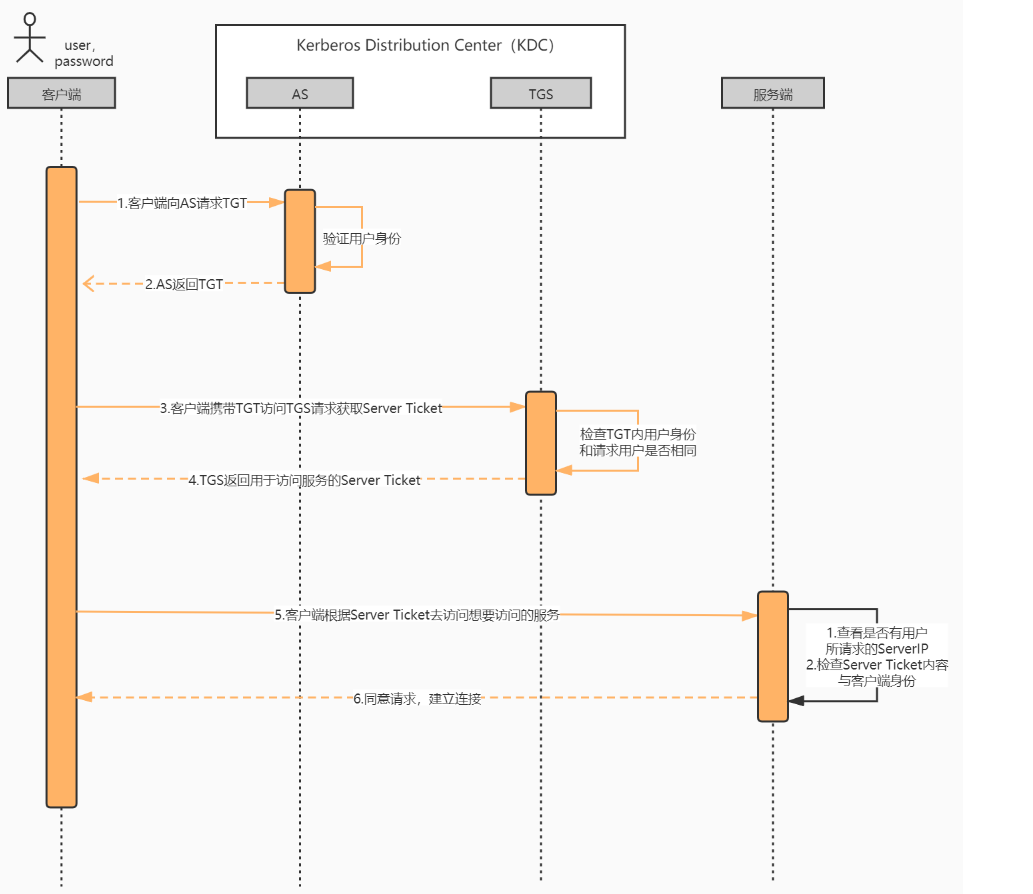
Kerberos简单介绍及使用
Kerberos作用 简单来说安全相关一般涉及以下方面:用户认证(Kerberos的作用)、用户授权、用户管理.。而Kerberos功能是用户认证,通俗来说解决了证明A是A 的问题。 认证过程(时序图) 核心角色/概念 KDC&…...

DOM编程-全选、全不选和反选
<!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title>全选、全不选和反选</title> </head> <body bgcolor"antiquewhite"> <script type"text/jav…...

C++11可变模板参数
C11可变模板参数一、简介二、语法三、可变模版参数函数3.1、递归函数方式展开参数包3.2、逗号表达式展开参数包一、简介 C11的新特性–可变模版参数(variadic templates)是C11新增的最强大的特性之一,它对参数进行了高度泛化,它能…...

Linux多线程
目录 一、认识线程 1.1 线程概念 1.2 页表 1.3 线程的优缺点 1.3.1 优点 1.3.2 缺点 1.4 线程异常 二、进程 VS 线程 三、Linux线程控制 3.1 POSIX线程库 3.1 线程创建 3.3 线程等待 3.4 线程终止 3.4.1 return退出 3.4.2 pthread_exit() 3.4.3 pthread_cancel…...
Webpack5 环境下 Openlayers 标注(Icon) require 引入图片问题
Webpack5 环境下 Openlayers 标注(Icon) require 引入图片问题环境版本Openlayers 使用 require 问题Webpack5 正确配置构建新环境的时候,偶然发现 Openlayers 使用 require 的方式加载图片(Icon)报错,开始…...

Zookeeper安装部署
文章目录Zookeeper安装部署Zookeeper安装部署 将Zookeeper安装包解压缩, [rootlocalhost opt]# ll 总用量 14032 -rw-r--r--. 1 root root 12392394 10月 13 11:44 apache-zookeeper-3.6.0-bin.tar.gz drwxrwxr-x. 6 root root 4096 10月 18 01:44 redis-5.0.4 …...
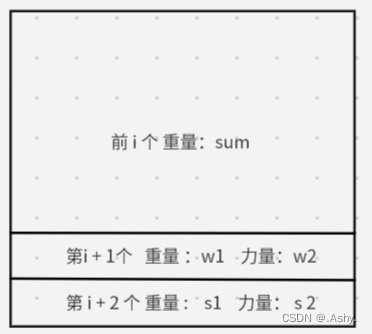
Cow Acrobats ( 临项交换贪心 )
题目大意: N 头牛 , 每头牛有一个重量(Weight)和一个力量(Strenth) , N头牛进行排列 , 第 i 头牛的风险值为其上所有牛总重减去自身力量 , 问如何排列可以使最大风险值最小 , 求出这个最小的最大风险值&am…...

MySQL:为什么说应该优先选择普通索引,尽量避免使用唯一索引
前言 在使用MySQL的过程中,随着表数据的逐渐增多,为了更快的查询我们需要的数据,我们会在表中建立不同类型的索引。 今天我们来聊一聊,普通索引和唯一索引的使用场景, 以及为什么说推荐大家优先使用普通索引…...

Spring Cloud alibaba之Feign
JAVA项目中如何实现接口调用?HttpclientHttpclient是Apache Jakarta Common下的子项目,用来提供高效的、最新的、功能丰富的支持Http协议的客户端编程工具包,并且它支持HTTP协议最新版本和建议。HttpClient相比传统JDK自带的URL Connection&a…...
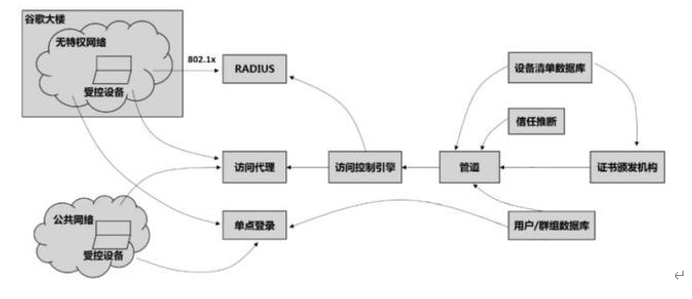
零信任-Google谷歌零信任介绍(3)
谷歌零信任的介绍? "Zero Trust" 是一种网络安全模型,旨在通过降低网络中的信任级别来防止安全威胁。在零信任模型中,不论请求来自内部网络还是外部网络,系统都将对所有请求进行详细的验证和审核。这意味着每次请求都需…...
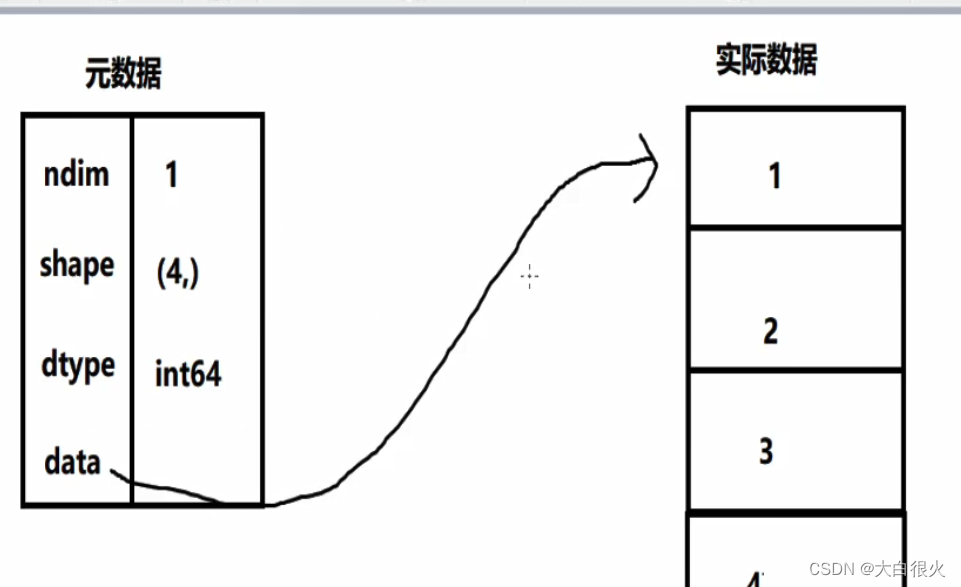
Numpy基础——人工智能基础
文章目录一、Numpy概述1.优势2.numpy历史3.Numpy的核心:多维数组4.numpy基础4.1 ndarray数组4.2 内存中的ndarray对象一、Numpy概述 1.优势 Numpy(Nummerical Python),补充了Python语言所欠缺的数值计算能力;Numpy是其它数据分析及机器学习库的底层库&…...

电商仓储与配送云仓是什么?
仓库是整个供给链的关键局部。它们是产品暂停和触摸的点,耗费空间和时间(工时)。空间和时间反过来也是费用。经过开发数学和计算机模型来微调仓库的规划和操作,经理能够显著降低与产品分销相关的劳动力本钱,进步仓库空间应用率,并…...

【零基础入门前端系列】—HTML介绍(一)
【零基础入门前端系列】—HTML介绍(一) 一、什么是HTML HTML是用来描述网页的一种语言HTML指的是超文本标记语言:HyperText Markup LanguageHTML不是一种编程语言,而是一种超文本标记语言,标记语言是一套标记标签(ma…...

Elasticsearch索引库和文档的相关操作
前言:最近一直在复习Elasticsearch相关的知识,公司搜索相关的技术用到了这个,用公司电脑配了环境,借鉴网上的课程进行了总结。希望能够加深自己的印象以及帮助到其他的小伙伴儿们😉😉。 如果文章有什么需要…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...
