前端工程师leetcode算法面试必备-二分搜索算法(下)索算法(下)
一、287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
1、HashMap
在没有其它附加条件的情况下,读者第一时间会想到通过 HashMap 来记录出现过的数字,从而找到重复数:
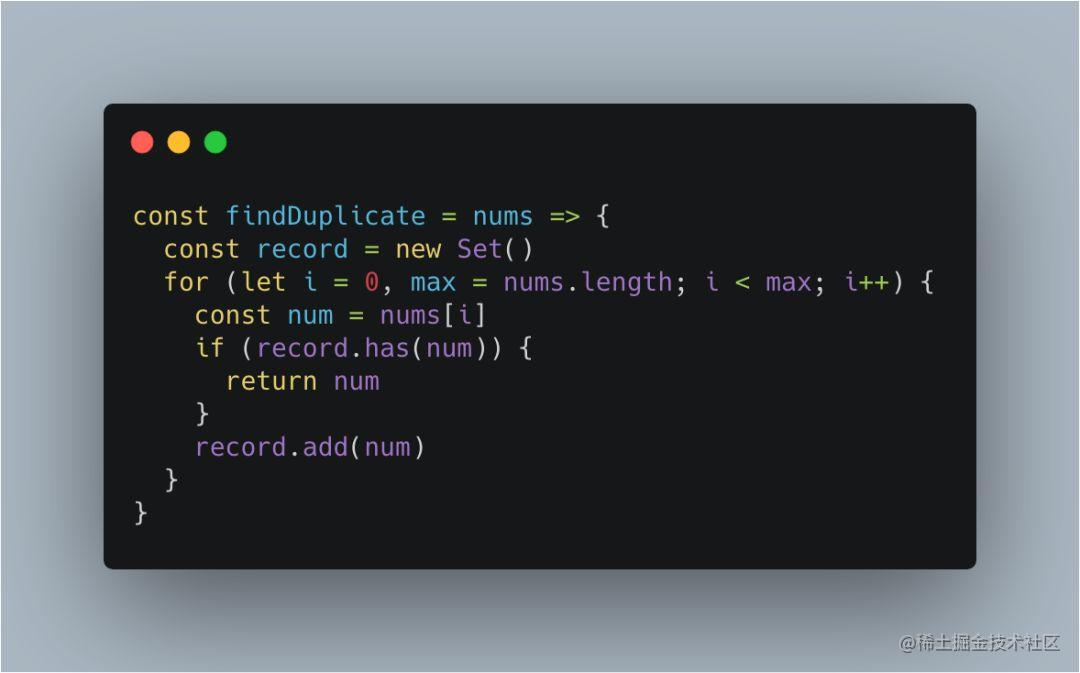
上述实现代码的时间复杂度和空间复杂度都为 O(n),如果只允许使用 O(1) 的空间复杂度,该如何解决这道题目呢?
2、Binary Search
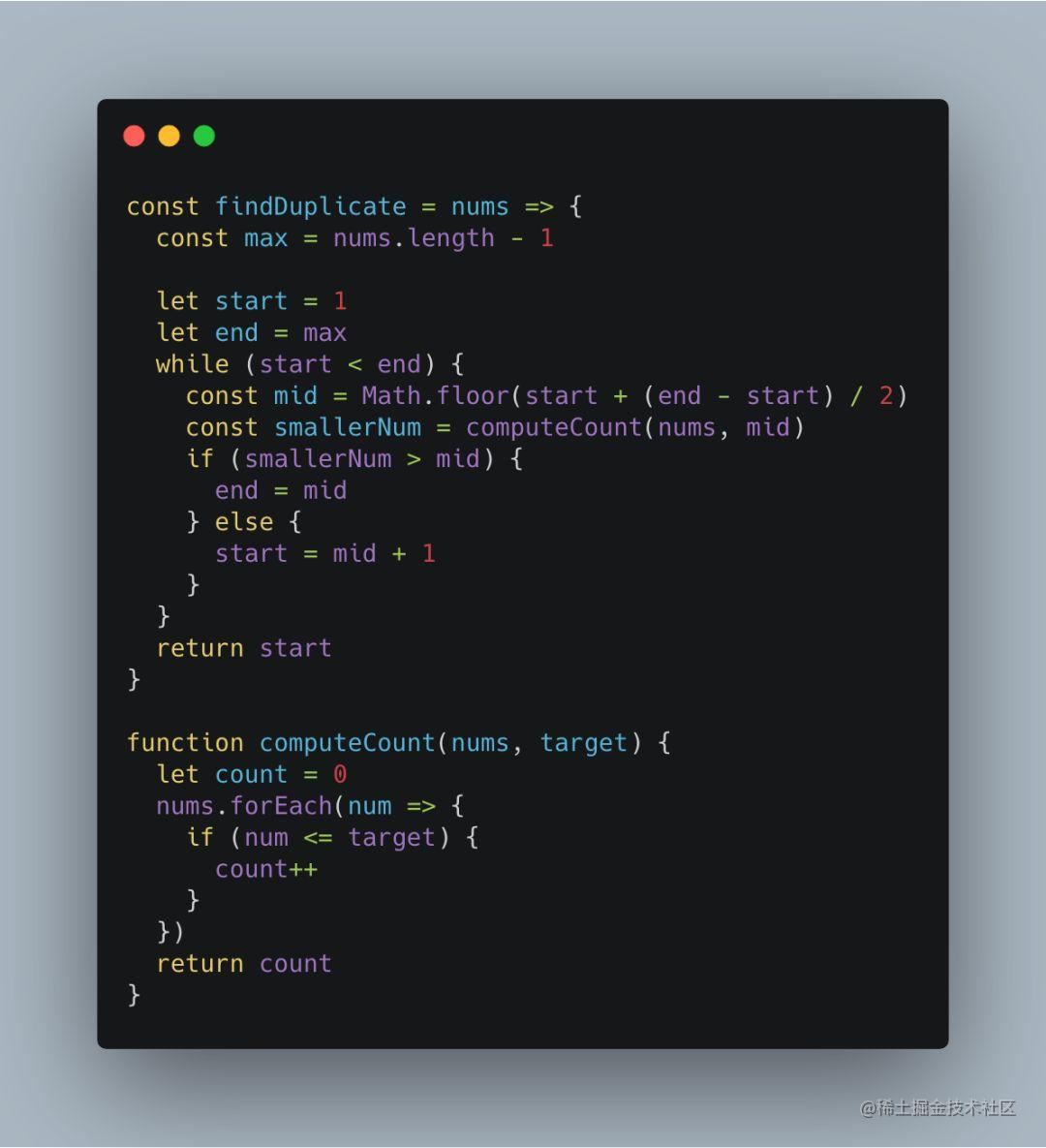
这种条件下,最容易想到的就是通过两重循环暴力搜索当前数字是否与后面的数字重复的方法来解决,但是这种方案的时间复杂度为 O(n^2),既然涉及到了搜索,就可以尝试通过二分搜索算法将时间复杂度降低到 O(nlogn)。
根据前面的刷题经验,可以很容易地找出有序数组:1 到 n 的递增整数序列。
接下来的难点就是通过重复数的特性来确定下一轮搜索区间是落在左半区间还是右半区间:
-
首先需要遍历 nums 数组,获取不大于当前中间数的数字的个数;
-
如果个数大于中间数,那么下一轮搜索区间落在左半区间;
-
如果个数小于中间数,那么下一轮搜索区间落在右半区间;
二、209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
1、Binary Search
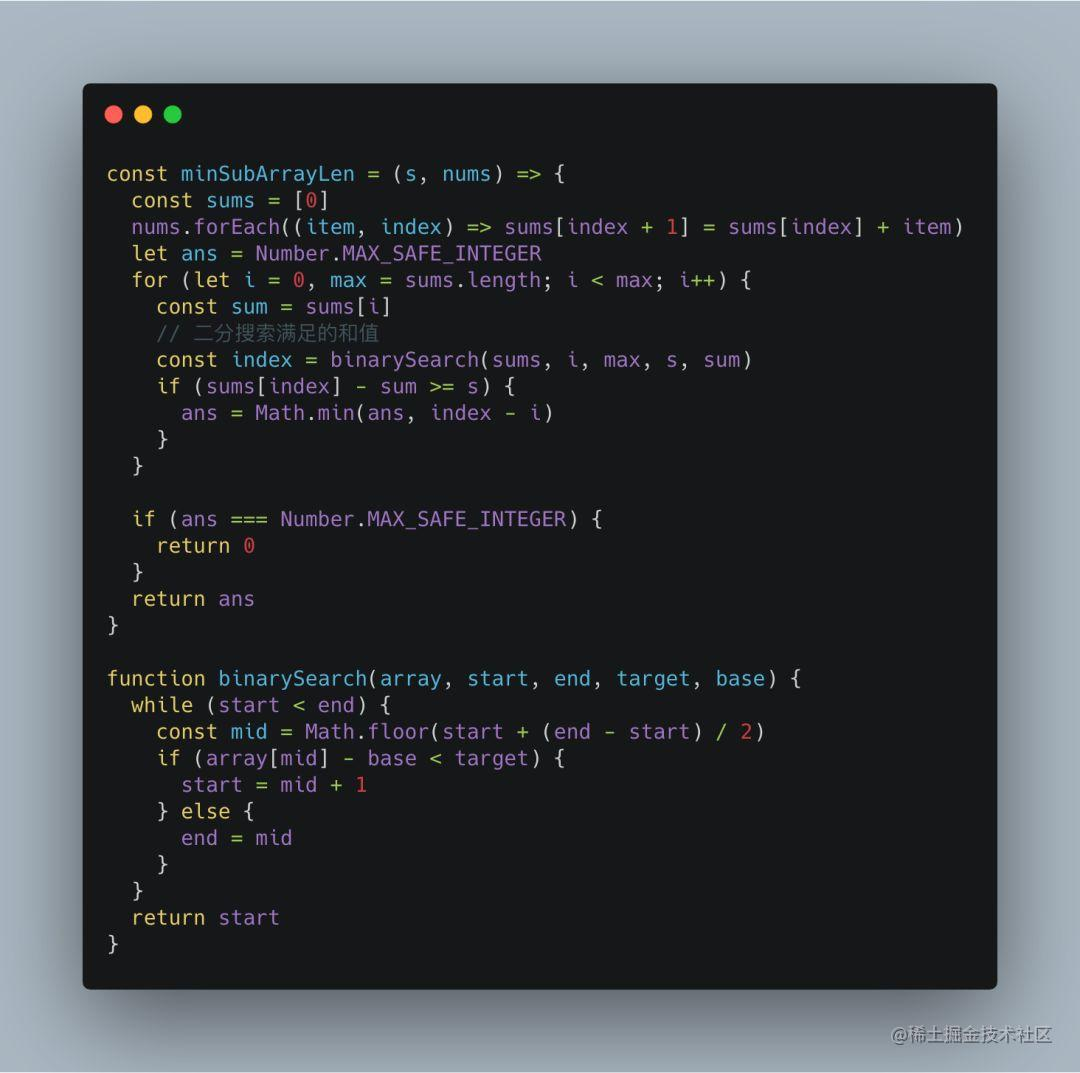
这道题目中的有序数组不太好找,需要用到一个技巧:构造前缀和数组。
nums = [2, 3, 1, 2, 4, 3]# 前缀和sums = [0, 2, 5, 6, 8, 12, 15]
从而上述示例中可以发现前缀和数组是一个有序数组,那么对于任意 i 到 j 的连续子数组之和,可以通过 sums[j+1] - sums[i] 求出。
并且根据前缀和的差值与 s 的比较,可以判断满足条件的连续子数组的终止下标落在哪个区间内。
参考视频:传送门
通过前缀和对数组的预处理以及二分搜索算法,时间复杂度为 O(nlogn)。
2、Two Points
除了上述二分搜索算法的处理方法之外,可能最简单暴力的方法就是通过嵌套循环找出长度最小的连续子数组,但是这种方法的时间复杂度为 O(n^2),有没有方法将其降低到 O(n) 的时间复杂度呢?。
这里就要提及一下滑动窗口算法,它常用于处理连续子元素问题,将嵌套循环问题转化为单循环问题。
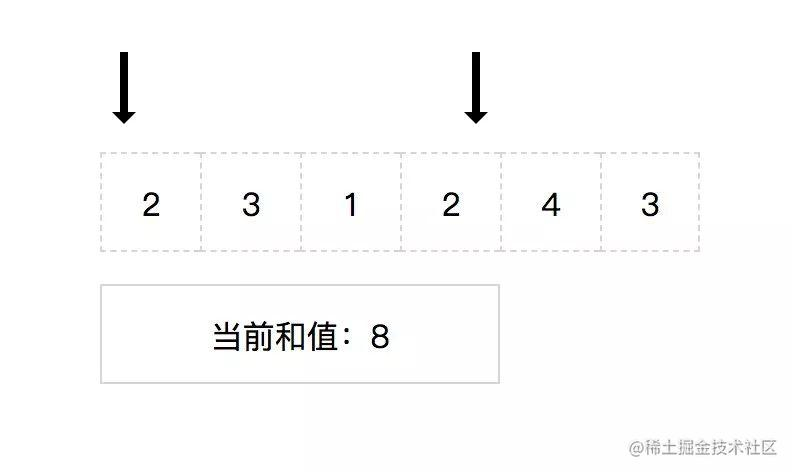
在本题中,通过头指针和尾指针维护当前连续子数组的和值窗口:
-
当前窗口的和值大于 s ,那么头指针向后移动一位;
-
当前窗口的和值小于 s ,那么尾指针向后移动一位;
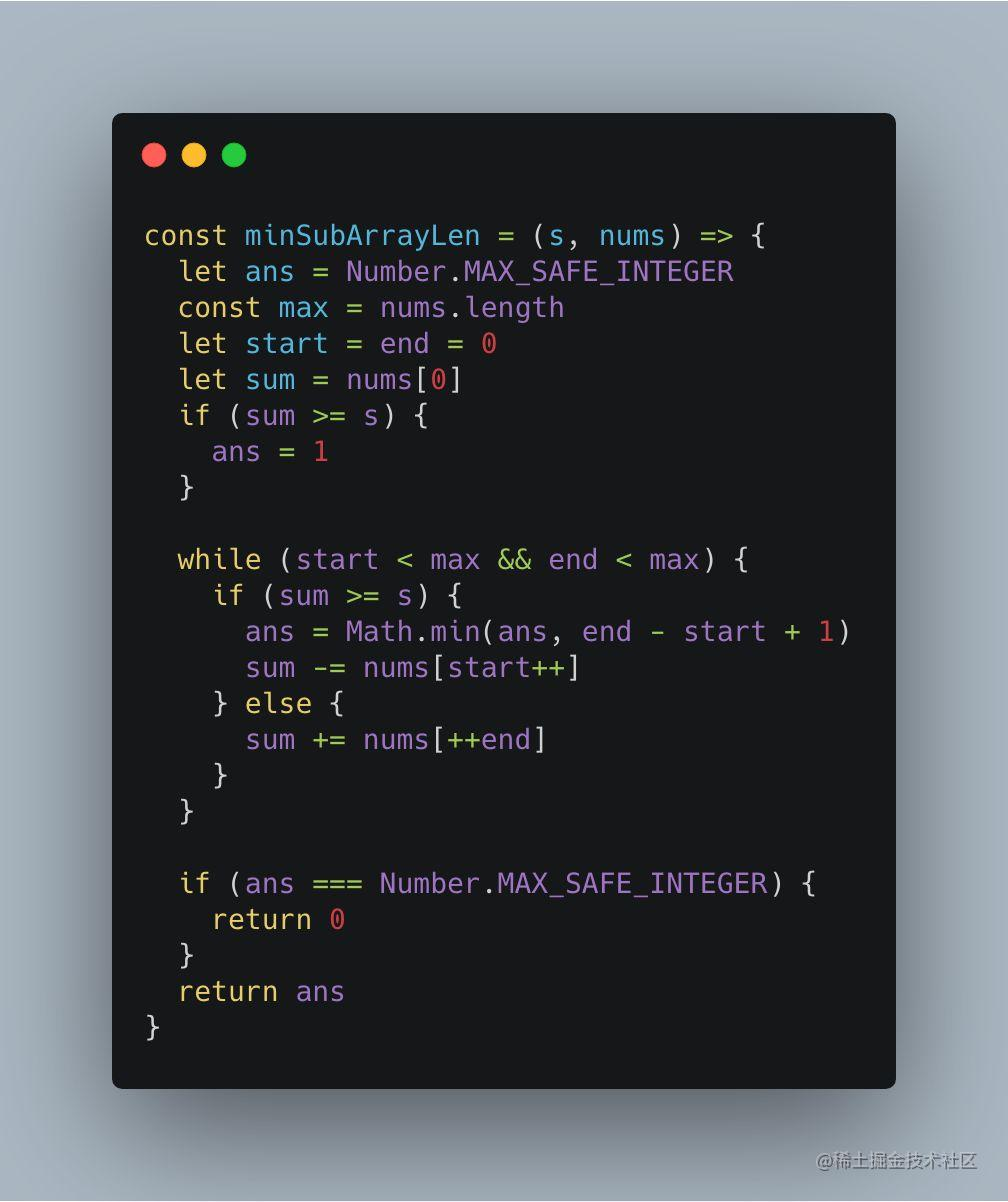
三、153. 寻找旋转排序数组中的最小值
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。请找出其中最小的元素。你可以假设数组中不存在重复元素。
这一类型的题目在 Easy 中也出现过,如:【852. 山脉数组的峰顶索引】和【162. 寻找峰值】。
本题中,原本的递增数组被转化成包含两个递增序列的数组,并且其中无重复元素,那么就可以得出:第一个递增数组中的任意一个元素都大于第二个递增数组中的元素。
有了这一关键信息,对于任一中间数,都可以将其与当前搜索区间的最后一个元素相比较,从而知道当前中间数在哪一个递增序列上,而所求的最小值存在于第二个递增序列的头部,那么不断将搜索区间往这一方向收缩,即可得到最小值:
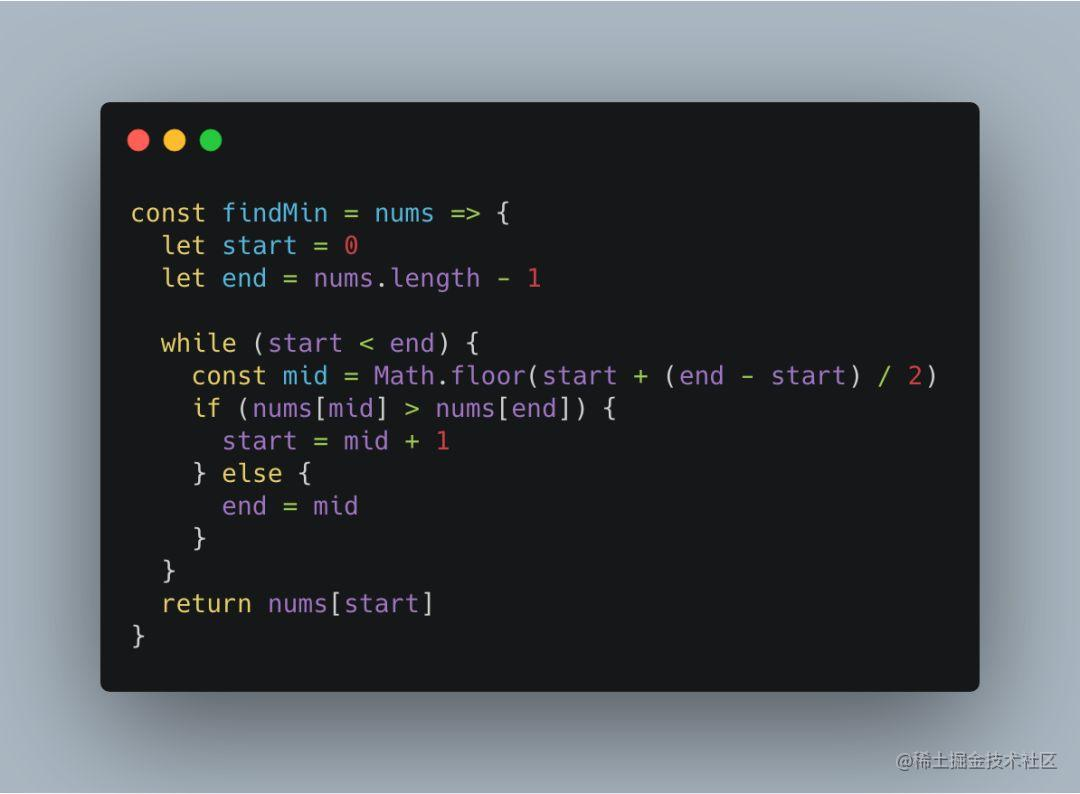
四、33. 搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。你可以假设数组中不存在重复的元素。你的算法时间复杂度必须是 O(log n) 级别。
这道题是【153. 寻找旋转排序数组中的最小值】的进阶题型。
在 153 中,只需要将搜索区间不断向第二个递增区间收缩,即可得到最小值。而本题中的目标值的位置并不确定,所以在每次确定搜索区间时,需要考虑很多种情况:
-
如果当前搜索区间只落在一个递增区间上,那么和一般的处理方法没什么异样;
-
如果当前搜索区间横跨两个递增区间,那么就需要根据中间数在第一个递增区间还是第二个递增区间上分别处理;
具体的条件判断,请查看下面的代码实现:

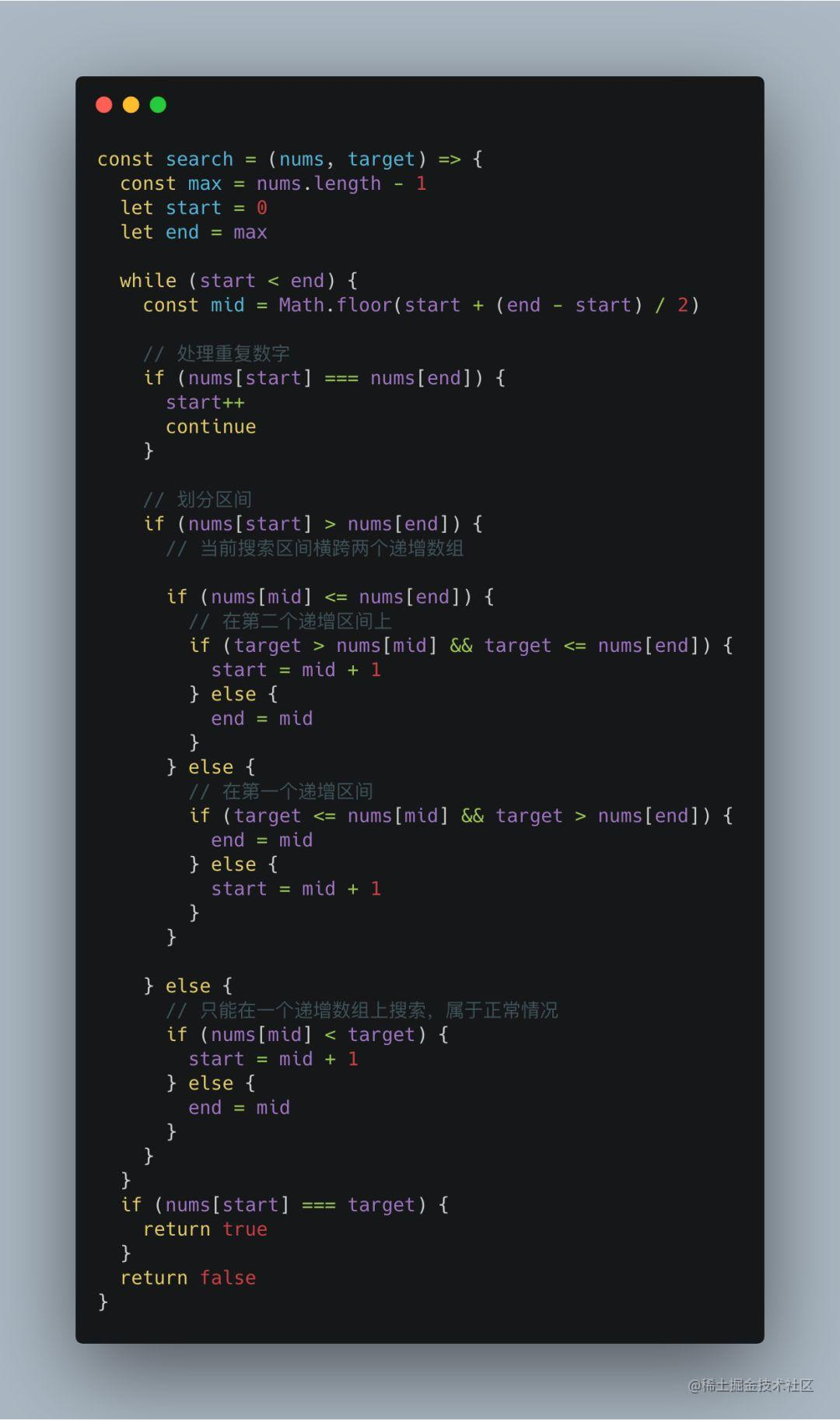
五、81. 搜索旋转排序数组 II
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true,否则返回 false。
这道题目在【33. 搜索旋转排序数组】的基础上去除了”不存在重复元素“这一条件。
回顾 33 题的解法,在寻找下一个搜索区间时,通过该搜索区间的头部元素和尾部元素的比较得出当前搜索区间是否横跨两个递增序列。一旦没有无重复元素这一条件,那么根据头尾两个元素无法判断当前搜索区间是否横跨两个递增序列。
本题要求计算元素的存在性,那么一个元素的重复元素对其存在性是没有任何影响的,所以只要在二分搜索的过程中,剔除掉头尾部的重复元素即可:
写在最后
算法作为计算机的基础学科,用 JavaScript 刷,一点也不丢人ε=ε=ε=┏(゜ロ゜;)┛。
本系列文章会分别给出一种算法的3种难度的总结篇(简单难度,中等难度以及困难难度)。在简单难度中,会介绍该算法的基本知识与实现,另外两个难度,着重讲解解题的思路。
如果本文对您有所帮助,可以点赞或者关注来鼓励博主。
相关文章:

前端工程师leetcode算法面试必备-二分搜索算法(下)索算法(下)
一、287. 寻找重复数 给定一个包含 n 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。 1、HashMap 在没有其它附加条件的情况下&…...
使用Autowired为什么会被IDEA警告,应该怎么修改最佳
问题原因 关于这个问题,其实答案相对统一,实际上用大白话说起来也容易理解。 初始化问题 先看一下Java初始化类的顺序:父类的静态字段 > 父类静态代码块 > 子类静态字段 > 子类静态代码块 > 父类成员变量 > 父类构造代码块 &…...
)
面向对象(中)
面向对象(中) 一、 面向对象之继承性 继承性的好处 减少代码的冗余,提高了代码的复用性。 便于功能的扩展。 为多态性的使用,提供了前提。 继承性的格式 class A extends B{} A:子类、派生类、subclass B:…...
【云原生】promehtheus整合grafana实现可视化监控实战
文章目录前言一. 实验环境二. 安装grafana2.1 grafana的介绍2.2 为什么选择grafana?2.3 grafana下载及安装三. 网页端配置grafana3.1 浏览器访问grafana网页3.2 使用grafana 获取prometheus的数据源3.3 grafana导入prometheus模板总结前言 大家好,又见面…...

Linux 内核定时器实验
目录 一、内核时间管理简介 二、内核定时器简介 三、驱动编写 1、修改makefile 2、添加定义 3、初始化led函数 4、添加调用 5、初始化定时器与定时器处理函数 这部分代码如下 四、ioctl函数 五、内核添加unlocked_ioctl 函数 1、添加设备操作集unlocked_ioctl成员 2…...
喜欢大屏电视?那就选择酷开系统,实现智能生活享受
随着科技的发展和我们生活水平的提高,越来越多的消费者开始认可并习惯使用各种高质量的科技产品,比如喜欢玩游戏的消费者,他们往往会追求流畅性更强、刷新率更快的大显示屏,以此获得更真实刺激的游戏体验,而喜欢追剧的…...

PMP应该如何备考?
备考之初的我们,总会四处搜索PMP备考经验,希望能拿到那些高分通关前辈的备考经验和方法。众所周知PMP考试因为有35个学时培训的基本要求,所以肯定是要通过培训机构报名的。 一,首先我们需要了解到新的考纲 1.PMP模块划分发生变化…...

AcWing《蓝桥杯集训·每日一题》—— 3956.截断数组
AcWing《蓝桥杯集训每日一题》—— 3956. 截断数组 文章目录AcWing《蓝桥杯集训每日一题》—— 3956. 截断数组一、题目二、解题思路三、代码实现本次博客我是通过Notion软件写的,转md文件可能不太美观,大家可以去我的博客中查看:北天的 BLOG…...
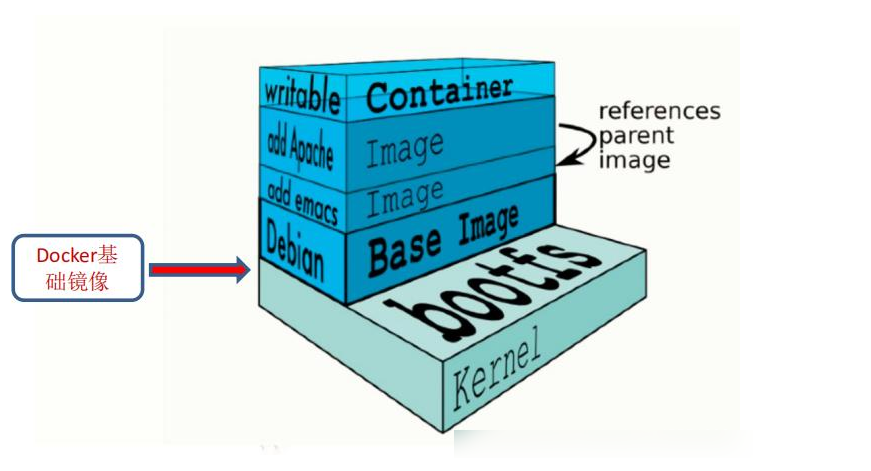
Docker的数据管理
一、管理docker容器中数据 管理Docker 容器中数据主要有两种方式:数据卷(Data Volumes)和数据卷容器( DataVolumes Containers) 。 1、 数据卷 数据卷是一个供容器使用的特殊目录,位于容器中。可将宿主机的目录挂载到数据卷上,对数据卷的修改操作立刻…...

RxJS处理异步数据流
什么是异步? 异步(Asynchronous)指的是不同步发生的事件或操作。通常,同步操作是指一系列代码按照顺序依次执行,直到当前代码块执行完毕后才继续执行下一个代码块;而异步操作则是指某些代码会被提交到后台执行&#…...

IP地址与用户行为
IP地址能够解决网络风险和提高网络安全的原因是:所有的网络请求都会带有IP信息,是访问者的独立标识,另外ip地址的分配和管理比较严格,难以造假。另外ip属于网络层,可以轻松的对其进行阻断。现有的各种网络安全、负载均…...

底层逻辑2
有些创业者,在3D打印⽕爆的时候做3D打印,在VR(虚拟现 实)蓬勃发展的时候转⾏做VR,在区块链成为热⻔话题的时候摇身⼀ 变成了区块链专家,⽽⼈⼯智能⽕了以后,他们⼜全身⼼投⼊⼈⼯智 能这⼀⾏。再…...

TCP报头详解及TCP十种核心机制(一)
目录 前言: TCP报头 TCP核心机制 一、确认应答 二、超时重传 小结: 前言: 这篇文章详细介绍了TCP报头中的一些核心数据,及两种TCP核心机制。其他的一些机制会在后面文章中详细介绍。 TCP报头 解释: 1ÿ…...

Linux用户的添加、修改和删除以及相关配置文件:useradd、passwd、usermod、userdel、相关配置文件
目录 账户的创建(useradd) 第一步:创建账号 第二步:创建密码 useradd参考文件 CROUP100 HOME/home INACTIVE-1 EXPIRE SHELL/bin/bash SKEL/etc/skel UID/GID密码参数参考:/etc/login.defs 密码参数显示命…...
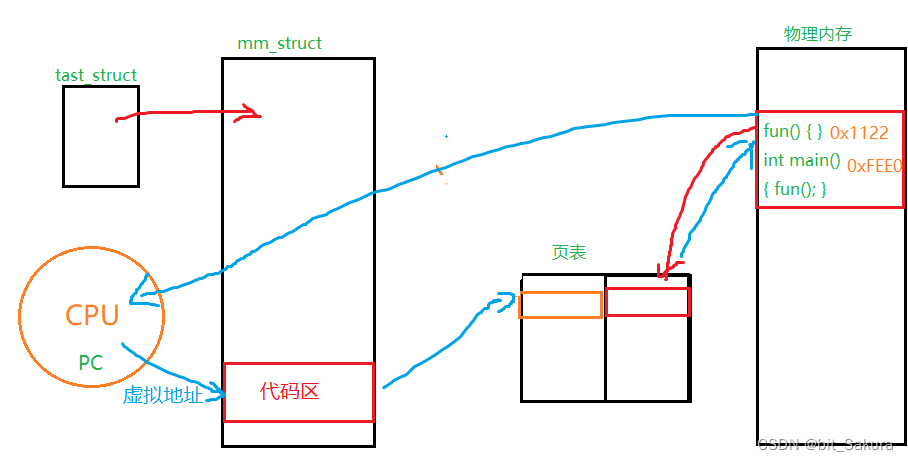
进程地址空间
目录 回顾C/C语言的程序地址空间 感性认识虚拟地址空间 虚拟地址空间与物理空间如何建立映射关系 为什么要虚拟地址空间? 回顾C/C语言的程序地址空间 在学习C/C语言时我们知道了一个概念叫程序地址空间。通俗来说就是如下一张表,从中可以得知系统的几…...
数楼梯(加强版)
数楼梯(加强版) 题目背景: 小明一天放学回家,看到从1楼到2楼共有n个台阶,因为好奇,他想尝试一下总共有几种方案到二楼?他可以1步,2步,3步的跳,不能跳3步以上. 他试了很多次都没有解决这个问题,于是请求聪明的你帮忙解决这个问题. 题目描述: 1楼到2楼楼梯有n级台阶。小明每…...

MySQL-数据类型
数据类型简介数据表由多列字段构成,每一个字段指定了不同的数据类型,指定了数据类型之后,也就决定了向字段插入的数据内容。不同的数据类型也决定了 MySQL 在存储它们的时候使用的方式,以及在使用它们的时候选择什么运算符号进行运…...

剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)
剑指 Offer 32 - II. 从上到下打印二叉树 II(java解题)1. 题目2. 解题思路3. 数据类型功能函数总结4. java代码5. 踩坑记录1. 题目 从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。 例如: 给定二叉…...

C#网络爬虫开发
1前言爬虫一般都是用Python来写,生态丰富,动态语言开发速度快,调试也很方便但是我要说但是,动态语言也有其局限性,笔者作为老爬虫带师,几乎各种语言都搞过,现在这个任务并不复杂,用我…...

Fastjson 总结
0x00 前言 这一篇主要是针对已经完成的fastjson系列做一个知识点总结,一来是为了更加有条理的梳理已经存在的内容,二来是为了更好的复习和利用。 0x01 Fastjson基础知识点 1.常见问题: 问:fastjson的触发点是什么?…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
