算法通关(3) -- kmp算法
KMP算法的原理
从题目引出
有两个字符串s1和s2,判断s1字符串是否包含s2字符串,如果包含返回s1包含s2的最左开头位置,不包含返回-1,如果是按照暴力的方法去匹配,以s1的每个字符作为开头,用s2的整体去匹配,那么得到的时间复杂度达到O(m*n),若字符串长度过长,那么可能导致不能AC。。。那么可不可以利用前面的匹配过程去帮助匹配加速,某些位置不用按照一个位置一个位置的去匹配。有的,这就是今天要了解的KMP算法。
1.next数组的定义
先知道是怎么回事就行
用s2去匹配s1,next数组是对于s2来说的;含义:不包含当前,它前面字符串前缀和后缀最大匹配长度,也不能包含整体:例如前面的字符串abc,如果包含整体,abc一定匹配abc,没有了意义.

对于0位置的a来说,它的前缀什么都没有,因此放一个-1表示不存在;对于1位置的a来说,前面有一个a,但是只有一个字母,不能够进行匹配,匹配则违反了包含整体(此时整体只有一个1),因此1位置是0;对于2位置b来说,前面是aa,前缀一个a,后缀一个a,刚好匹配,因此填1;

对于3位置的a来说,前面是aab,取一个(前缀是a,后缀是b,不行),取两个(前缀是aa,后缀是ab,不行),因此是0.。。。依次类推,对于6位置的x来说,前面是aabaab,最长匹配字符串是3,因此填3;

同理:对于12位置的a来说,选择5个是最大的匹配长度。 记住,不包含当前下标的字符!!!
2.如何加速匹配?

匹配到13位置不相同,下次位置从哪里匹配?匹配不上的next位置是6,那么让s2的6位置的c去匹配s1的13位置,也就是说,前面的1~6位置被放弃了!!!这里引出两个问题:
1:为什么放弃前面的?2:s2的0~5位置为什么不用验证,可以直接从6位置的c开始和s1的13进行匹配?
第二个问题:
先回答第二个问题:因为next数组是不包含当前,它前面字符串前缀和后缀最大匹配长度,为什么是6,因为那个位置的s2字符串前面数6个和后面数6个得到的字符串相同!!!如图:
由于s1和s2的匹配,可知m1和n1相同,m2和n2相同,又因为next数组,n2和n1相同,那么这四个都相同,就可以得出n1和m2相同,既然相同了,那么就没必要费时间从头开始了。继续匹配如下图:

第一个问题:

四个红色方框长度相同.上面说的是s2从k位置开始匹配,假设可以从小于k的位置进行匹配,例如图中的m位置,因为s1的m位置之后和s2之后的字符相同(不包含j位置,因为是从哪里进行的退出),
从m位置进行匹配可以成功,那么s1的绿色和s2的绿色(下边)一定可以匹配成功,由于s1的绿色第一次匹配时和s2的绿色(上边)匹配成功,因此可以得到s2的这两端绿色是相同的字符串
而这个长度超过了next数组给定的长度,因为只要匹配上,next算的是不包含当前,它前面字符串前缀和后缀最大匹配长度,违背了next记录最大长度。这样子就加速了匹配的进程
3.KMP算法代码
int kmp(const string& s1, const string& s2) {// x是s1的比对位置// y是s2的比对位置int n = s1.length(), m = s2.length(), x = 0, y = 0; // 获取next数组 vector<int> next = nextArray(s2, m);// 不越界while (x < n && y < m) {if (s1[x] == s2[y]) {// 每个位置可以匹配的上x++;y++;}// 当前不等else if (y == 0) {// 如果是s2的0位置没有匹配出来,无法往前跳了// s1换个位置开头吧,s2不动x++;}else {// s2的其他位置没有匹配出来,按照s2的y位置的next[y]跳跃// s1不动,s2换个位置配y = next[y];}}// s2匹配ok了,就找到了// 越界还没有找的,返回-1return y == m ? x - y : -1;
}4.next数组如何快速生成

按照前面的next值求下一个位置的next值
情况1:不用跳
求得“?”位置的next值,看的是前面字符的最大匹配长度,得知是8;也可以看前面“x”位置的next值,是7,看他与7位置的字符是否相同,这里相同,因为不相同就必须跳了,那就+1,得到8,为什么不能够更长呢?如图:
情况2:需要跳
用图来说吧

如果没有对上,继续跳,如果跳到头都没有跳出来,那么要求的next就是0。
为什么这样子,其实找的前缀和后缀都是在s2这个字符串中,即在一个字符串中找到尽可能的长的前缀和后缀,这就是next数组的含义,因为要保留尽量长!!!举个例子
5:next数组代码
vector<int> nextArray(const string& s, int m) {// m是字符串s2的长度if (m == 1) {return { -1 };}// next的第一个位置和第二个位置是固定的vector<int> next(m);next[0] = -1;next[1] = 0;// 从第二个位置开始填int i = 2, cn = 0;// 没有越界while (i < m) {// i 表示当前要求的next值的位置// cn表示当前要和一个字符比对的下标if (s[i - 1] == s[cn]) {// 后面的字符是cn位置// 为什么是++cn,而不是cn+1// 因为为了下面可能用到cn的值,如果后面的字符是cn位置,那么直接用// 当前位置求完了,求下一个位置就是++next[i++] = ++cn;}else if (cn > 0) {// 不一样,向前跳cn = next[cn];}else {// 已经等于0了,再往前跳到-1位置next[i++] = 0;}}// 得到next数组return next;
}KMP算法相关题目
题目1:
P4391 [BOI2009] Radio Transmission 无线传输 - 洛谷 | 计算机科学教育新生态
总长度是k个最短长度(设为n)的字串加上尾巴的一些,尾巴长度为L,那么总长度为k*n+L,前缀最大的长度串是(k-1)*n+L,因为此例中是以a开头,下一个a是经过了一次循环后的a,因此可以得到最大长度串。

两个疑惑:它可以更短吗?不可以,因为next求得就是它前面字符串前缀和后缀最大匹配长度。
它可以更长吗?不可以,举个例子:


因此可以得出结论:不能够变得更短,也不能变得更长!!!
代码如下:
#include <iostream>
#include <vector>
#include <string>using namespace std;
const int MAXN = 1000001;
int next_[MAXN];
int n;
string s;void nextArray() {next_[0] = -1;next_[1] = 0;int i = 2, cn = 0;while (i <= n) {if (s[i - 1] == s[cn]) {next_[i++] = ++cn;}else if (cn > 0) {cn = next_[cn];}else {next_[i++] = 0;}}
}int compute() {nextArray();return n - next_[n];
}int main() {cin >> n;cin >> s;cout << compute() << endl;return 0;
}题目2:
[USACO15FEB] Censoring S - 洛谷
利用栈,压入s1位置字符的下标以及s2位置字符的下标。
如果位置字符下标的值对应,那么两个字符向前++,当s2越界了,那么表示s1的一段和s2匹配上了,那么使栈的长度-s2的长度,然后根据栈顶元素的下标,让s2找到正确的下标。如图:
代码如下:
#include <iostream>
#include <vector>
#include <string>using namespace std;const int MAXN = 1000001;
int next_[MAXN];
// 栈1压s1,栈2压s2
int stack1[MAXN];
int stack2[MAXN];
int _size;
string s1, s2;// 生成s2的next数组
void nextArray(int m) {next_[0] = -1;next_[1] = 0;int i = 2, cn = 0;while (i < m) {if (s2[i - 1] == s2[cn]) {next_[i++] = ++cn;}else if (cn > 0) {cn = next_[cn];}else {next_[i++] = 0;}}
}void compute() {_size = 0;int n = s1.length(), m = s2.length(), x = 0, y = 0;// s2的next数组nextArray(m);while (x < n) {if (s1[x] == s2[y]) {// 对应的上,s1和s2两者++stack1[_size] = x;stack2[_size] = y;_size++;x++;y++;}// 对应不上,而且y来到s2的开头位置else if (y == 0) {// stack1[_size] = x;stack2[_size] = -1;_size++;x++;}// 对应不上,没来到开头位置,往前跳else {y = next_[y];}// s2遍历完了if (y == m) {// 相当于栈直接弹出了m条记录_size -= m;// 处理s2的y// 栈中有东西,跳到栈顶的下一个位置// 没有就是0下标y = _size > 0 ? (stack2[_size - 1] + 1) : 0;}}
}int main() {cin >> s1 >> s2;compute();for (int i = 0; i < _size; i++) {cout << s1[stack1[i]];}cout << endl;return 0;
}
相关文章:

算法通关(3) -- kmp算法
KMP算法的原理 从题目引出 有两个字符串s1和s2,判断s1字符串是否包含s2字符串,如果包含返回s1包含s2的最左开头位置,不包含返回-1,如果是按照暴力的方法去匹配,以s1的每个字符作为开头,用s2的整体去匹配,…...

5G网卡network connection: disconnected
日志 5G流程中没有报任何错误,但是重新拿地址了,感觉像是驱动层连接断开了,dmesg中日志如下: [ 1526.558377] ippassthrough:set [ ip10.108.40.47 mask27 ip_net10.108.40.32 router10.108.40.33 dns221.12.1.227 221.12.33.227] br-lan […...

微积分复习笔记 Calculus Volume 1 - 4.9 Newton’s Method
4.9 Newton’s Method - Calculus Volume 1 | OpenStax...

Flutter自定义矩形进度条实现详解
在Flutter应用开发中,进度条是一个常见的UI组件,用于展示任务的完成进度。本文将详细介绍如何实现一个支持动画效果的自定义矩形进度条。 功能特点 支持圆角矩形外观平滑的动画过渡效果可自定义渐变色可配置边框宽度和颜色支持进度更新动画 实现原理 …...

如何设置 TORCH_CUDA_ARCH_LIST 环境变量以优化 PyTorch 性能
引言 在深度学习领域,PyTorch 是一个广泛使用的框架,它允许开发者高效地构建和训练模型。为了充分利用你的 GPU 硬件,正确设置 TORCH_CUDA_ARCH_LIST 环境变量至关重要。这个变量告诉 PyTorch 在构建过程中应该针对哪些 CUDA 架构版本进行优…...

CSS的三个重点
目录 1.盒模型 (Box Model)2.位置 (position)3.布局 (Layout)4.低代码中的这些概念 在学习CSS时,有三个概念需要重点理解,分别是盒模型、定位、布局 1.盒模型 (Box Model) 定义: CSS 盒模型是指每个 HTML 元素在页面上被视为一个矩形盒子。…...

【笔记】前后端互通中前端登录无响应
后来的前情提要 : 后端的ip地址在本地测试阶段应该设置为localhost 前端中写cors的配置 后端也要写cors的配置 且两者的url都要为localhost 前端写的baseUrl是指定对应的后端的ip地址以及端口号 很重要 在本地时后端的IP的地址也必须为本地的 F12的网页报错是&a…...

AI引领PPT创作:迈向“免费”时代的新篇章?
AI引领PPT创作:迈向“免费”时代的新篇章? 在信息爆炸的时代,演示文稿(PPT)作为传递信息和展示观点的重要工具,其制作效率和质量直接关系到演讲者的信息传递效果。随着人工智能(AI)…...

HTB:Perfection[WriteUP]
目录 连接至HTB服务器并启动靶机 1.What version of OpenSSH is running? 使用nmap对靶机TCP端口进行开放扫描 2.What programming language is the web application written in? 使用浏览器访问靶机80端口页面,并通过Wappalyzer查看页面脚本语言 3.Which e…...

鸿蒙next打包流程
目录 下载团结引擎 添加开源鸿蒙打包支持 打包报错 路径问题 安装DevEcoStudio 可以在DevEcoStudio进行打包hap和app 包结构 没法直接用previewer运行 真机运行和测试需要配置签名,DevEcoStudio可以自动配置, 模拟器安装hap提示报错 安装成功,但无法打开 团结1.3版本新增工具…...

uni-app 实现自定义底部导航
原博:https://juejin.cn/post/7365533404790341651 在开发微信小程序,通常会使用uniapp自带的tabBar实现底部图标和导航,但现实有少量应用使用uniapp自带的tabBar无法满足需求,这时需要自定义底部tabBar功能。 例如下图的需求&am…...

Vue前端开发:animate.css第三方动画库
在实际的项目开发中,如果自定义元素的动画,不仅效率低下,代码量大,而且还存在浏览器的兼容性问题,因此,可以借助一些优秀的第三动画库来协助完成动画的效果,如animate.css和gsap动画库ÿ…...

Java中的I/O模型——BIO、NIO、AIO
1. BIO(Blocking I/O) 1. 1 BIO(Blocking I/O)模型概述 BIO,即“阻塞I/O”(Blocking I/O),是一种同步阻塞的I/O模式。它的主要特点是,当程序发起I/O请求(比如…...
)
【软考知识】敏捷开发与统一建模过程(RUP)
敏捷开发模式 概述敏捷开发的主要特点包括:敏捷开发的常见实践包括:敏捷开发的优势:敏捷开发的挑战:敏捷开发的方法论: ScrumScrum 的核心概念Scrum 的执行过程Scrum 的适用场景 极限编程(XP)核…...
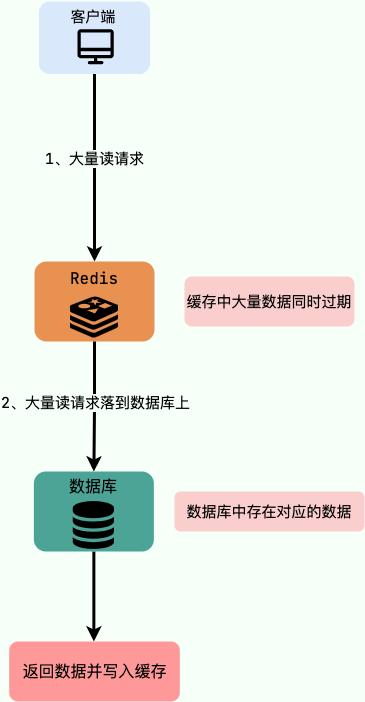
Redis常见面试题(二)
Redis性能优化 Redis性能测试 阿里Redis性能优化 使用批量操作减少网络传输 Redis命令执行步骤:1、发送命令;2、命令排队;3、命令执行;4、返回结果。其中 1 与 4 消耗时间 --> Round Trip Time(RTT,…...
业务模块部署
一、部署前端 1.1 window部署 下载业务模块前端包。 (此包为耐威迪公司发布,请联系耐威迪客服或售后获得) 包名为:业务-xxxx-business (注:xxxx为发布版本号) 此文件部署位置为:……...

【LeetCode】【算法】48. 旋转图像
LeetCode 48. 旋转图像 题目描述 给定一个 n n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。 你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。 思路 思路:再次拜见K神…...

【STM32F1】——9轴姿态模块JY901与串口通信(上)
【STM32F1】——9轴姿态模块JY901与串口通信(上) 一、简介 本篇主要对调试JY901模块的过程进行总结,实现了以下功能。 串口普通收发:使用STM32F103C8T6的USART2实现9轴姿态模块JY901串口数据的读取,并利用USART1发送到串口助手。 串口DMA收发:使用STM32F103C8T6的USART…...

Docker网络概述
1. Docker 网络概述 1.1 网络组件 Docker网络的核心组件包括网络驱动程序、网络、容器以及IP地址管理(IPAM)。这些组件共同工作,为容器提供网络连接和通信能力。 网络驱动程序:Docker支持多种网络驱动程序,每种驱动程…...

Vite与Vue Cli的区别与详解
它们的功能非常相似,都是提供基本项目脚手架和开发服务器的构建工具。 主要区别 Vite在开发环境下基于浏览器原生ES6 Modules提供功能支持,在生产环境下基于Rollup打包; Vue Cli不区分环境,都是基于Webpack。 在生产环境下&…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
