【动态规划】斐波那契数列模型总结
一、第 N 个泰波那契数
题目链接: 第 N 个泰波那契数
题目描述:

题目分析:
1、状态表示:
dp[i] 表示:第 i 个斐波那契数的值
2、状态转移方程:
由题意可知第 i 个数等于其前三个数之和
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3、初始化:
由于递推公式中存在 i-1、i-2、i-3,当 i=0、1、2的时候,就会出现-1,-2,-3这种非法的下标值,导致数组访问异常。因此,我们需要在填表前将 0,1,2 位置的值初始化。题目中也直接告诉了我们这些位置的初始值:
dp[0]=0 、 dp[1]=1 、 dp[2]=1
4、优化
其实每次在求取 dp[i] 的时候,只需要知道其前三个元素的值即可。也就是说我们在每次更新后只需要保存最后的三个数即可。通过三个数的值就能更新出下一个 dp 值。
代码实现:
class Solution {public int tribonacci(int n) {int[] dp=new int[]{0,1,1};if(n==0)return 0;if(n<3)return 1;for(int i=3;i<=n;i++){dp[i%3]=dp[0]+dp[1]+dp[2];}return dp[n%3];}
}
二、三步问题
题目链接: 三步问题
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
到达第 i 级台阶的所有方法我们不好确定,但我们可以确定到达第 i 级台阶的上一步只有三种可能:
- 从 i-1置上一级台阶,且到达 i-1 位置的方法数为 dp[i-1]
- 从 i-2置上二级台阶,且到达 i-2 位置的方法数为 dp[i-2]
- 从 i-3置上三级台阶,且到达 i-3 位置的方法数为 dp[i-3]
而到达第 i 级台阶的方法数就应该为其所有上一步的方式之和:
因此dp[i]=dp[i-1] + dp[i-2] + dp[i-3]
注意:由于这里计算的结果可能会很大。因此我们需要对结果进行取模。并且为了防止求和时溢出,在每次求和时都要先取模再求和
3、初始化:
由于递推公式中存在 i-1、i-2、i-3,当 i=0、1、2的时候,就会出现-1,-2,-3这种非法的下标值,导致数组访问异常。因此,我们需要在填表前将 0,1,2 位置的值初始化。由题意很容易就能求出这些位置的初始值:
dp[0]=1 、 dp[1]=2 、 dp[2]=4
代码实现:
class Solution {public int waysToStep(int n) {if(n==1||n==2)return n;if(n==3)return 4;int[] dp=new int[n+1];dp[1]=1;dp[2]=2;dp[3]=4;int MOD=(int)1e9+7;for(int i=4;i<=n;i++){dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;}return dp[n];}
}
三、 使用最小花费爬楼梯
题目链接:使用最小花费爬楼梯
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
- 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 1] + csot[i - 1]
- 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 2] + csot[i - 2]
我们每次只需要取两种情况的最小值即可。
因此:dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3、初始化:
很明显 i=0 或 i=1时是无法使用递推公式的。因此我们需要先把他们给初始化了。
由题意可得 dp[0] = dp[1] = 0 ,因为可以直接选择从第0级或第1级台阶开始爬楼梯,不需要任何花费。
代码实现:
class Solution {public int minCostClimbingStairs(int[] cost) {int n=cost.length;int[] dp=new int[n+1];for(int i=2;i<=n;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
}
四、解码方法
题目链接: 解码方法
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
- 让 i 位置上的数单独解码成⼀个字⺟;
- 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。
- 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;
- 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
- 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码⽅法,原因同上。此时 dp[i] = dp[i - 2]
- 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 ...... 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。
- 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1]
- 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] += dp[i - 2]
- 如果上述两个判断都不成⽴,说明没有解码⽅法, dp[i] 就是默认值 0 。
3、初始化:
代码实现:
class Solution {public int numDecodings(String s) {char[] cs=s.toCharArray();int n=s.length();if(cs[0]-'0'==0)return 0;int[] dp=new int[n+1];dp[1]=1;dp[0]=1;for(int i=2;i<=n;i++){if(cs[i-1]-'0'!=0)dp[i]=dp[i-1];if(cs[i-2]-'0'==0)continue;int x=(cs[i-2]-'0')*10+cs[i-1]-'0';if(x<=26){dp[i]+=dp[i-2];}}return dp[n];}
}
那么本篇文章就到此为止了,如果觉得这篇文章对你有帮助的话,可以点一下关注和点赞来支持作者哦。如果有什么讲的不对的地方欢迎在评论区指出,希望能够和你们一起进步✊

相关文章:

【动态规划】斐波那契数列模型总结
一、第 N 个泰波那契数 题目链接: 第 N 个泰波那契数 题目描述: 题目分析: 1、状态表示: dp[i] 表示:第 i 个斐波那契数的值 2、状态转移方程: 由题意可知第 i 个数等于其前三个数之和 dp[i] dp[i-…...

EasyUI弹出框行编辑,通过下拉框实现内容联动
EasyUI弹出框行编辑,通过下拉框实现内容联动 需求 实现用户支付方式配置,当弹出框加载出来的时候,显示用户现有的支付方式,datagrid的第一列为conbobox,下来选择之后实现后面的数据直接填充; 点击新增:新…...
使用 PageOffice 实现word文件在线留痕)
国产linux系统(银河麒麟,统信uos)使用 PageOffice 实现word文件在线留痕
PageOffice 国产版 :支持信创系统,支持银河麒麟V10和统信UOS,支持X86(intel、兆芯、海光等)、ARM(飞腾、鲲鹏、麒麟等)、龙芯(LoogArch)芯片架构。 查看本示例演示效果 …...
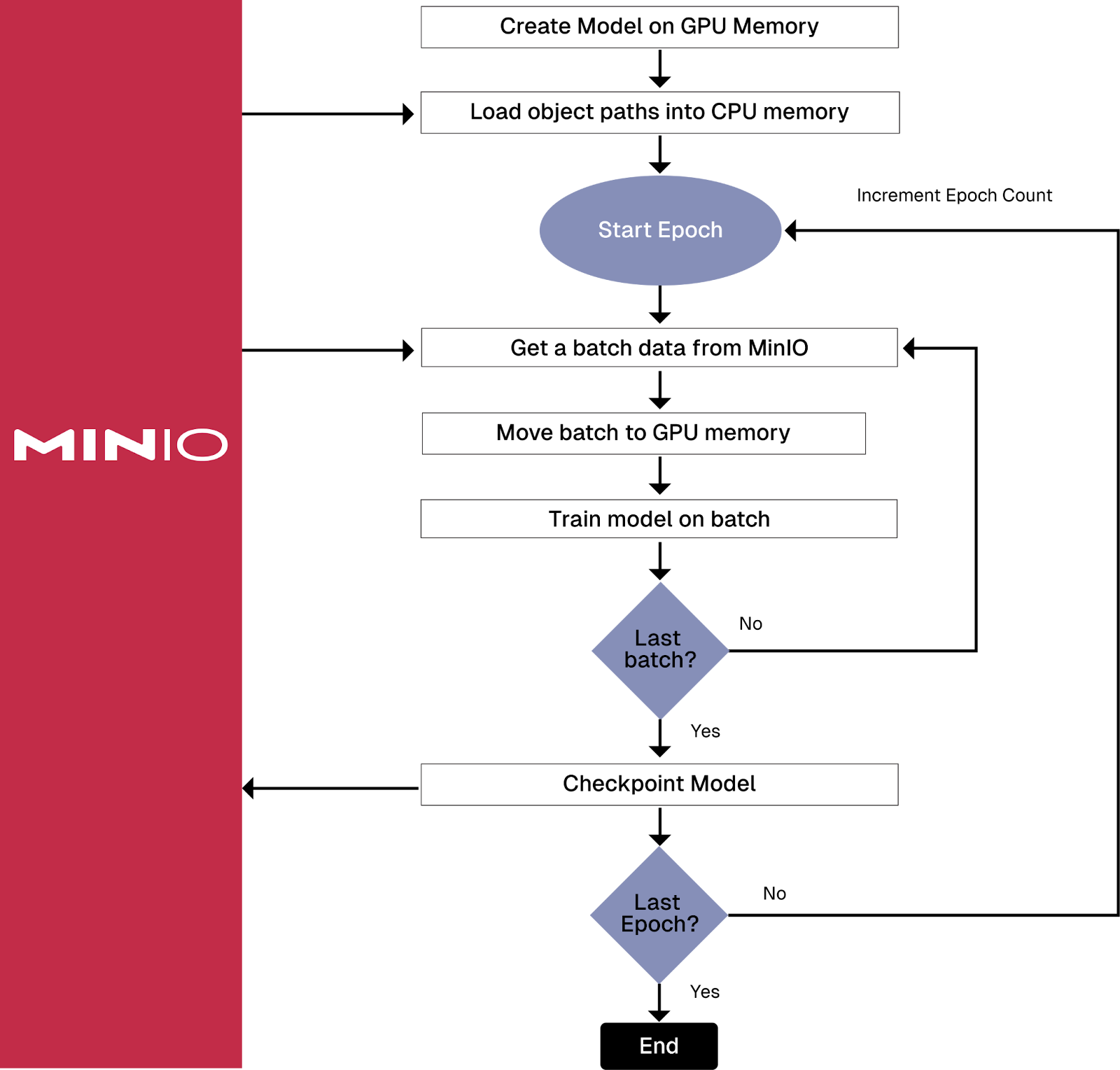
使用亚马逊 S3 连接器为 PyTorch 和 MinIO 创建地图式数据集
在深入研究 Amazon 的 PyTorch S3 连接器之前,有必要介绍一下它要解决的问题。许多 AI 模型需要使用无法放入内存的数据进行训练。此外,许多为计算机视觉和生成式 AI 构建的真正有趣的模型使用的数据甚至无法容纳在单个服务器附带的磁盘驱动器上。解决存…...

自动化运维:提升效率与稳定性的关键技术实践
自动化运维:提升效率与稳定性的关键技术实践 在数字化转型的浪潮中,企业对于IT系统的依赖日益加深,系统的复杂性和规模也随之膨胀。面对这一挑战,传统的运维模式——依靠人工进行服务器的监控、配置变更、故障排查等任务…...

Google Go编程风格指南-介绍
关于 首先应该明确的是:Go语言是Google搞出来的,这个编程风格指南也是它提出来的,详见:https://google.github.io/styleguide/go/。 然后国内翻译组跟上,于是有了中文版:https://gocn.github.io/stylegui…...

思科模拟器路由器配置实验
一、实验目的 了解路由器的作用。掌握路由器的基本配置方法。掌握路由器模块的使用和互连方式。 二、实验环境 设备: 2811 路由器 1 台计算机 2 台Console 配置线 1 根网线若干根 拓扑图:实验拓扑图如图 8-1 所示。计算机 IP 地址规划:如表…...

机器学习—选择激活函数
可以为神经网络中的不同神经元选择激活函数,我们将从如何为输出层选择它的一些指导开始,事实证明,取决于目标标签或地面真相标签y是什么,对于输出层的激活函数,将有一个相当自然的选择,然后看看激活函数的选…...

[ Linux 命令基础 4 ] Linux 命令详解-文本处理命令
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

Odoo:免费开源的钢铁冶金行业ERP管理系统
文 / 开源智造 Odoo亚太金牌服务 简介 Odoo免费开源ERP集成计质量设备大宗原料采购,备件设材全生命周期,多业务模式货控销售,全要素追溯单品,无人值守计量物流,大宗贸易交易和精细化成本管理等方案;覆盖…...

33.Redis多线程
1.Redis队列与Stream Redis5.0 最大的新特性就是多出了一个数据结构 Stream,它是一个新的强大的支持多播的可持久化的消息队列。 Redis Stream 的结构如上图所示,每一个Stream都有一个消息链表,将所有加入的消息都串起来,每个消息都有一个唯…...

【Python】解析 XML
1、Python 对 XML 的解析 1.1 SAX (simple API for XML ) SAX 解析器使用事件驱动模型,通过在解析XML的过程中触发一个个的事件并调用用户定义的回调函数来处理XML文件。 xml.sax 模块牺牲了便捷性来换取速度和内存占用。 事件驱动指一种基于回调(ca…...

【复平面】-复数相乘的几何性质
文章目录 从数学上证明1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z22. 应用三角恒等式3. 得出结果 从几何角度证明1.给出待乘的复数 u i u_i ui2.给出任意复数 l l l3.复数 l l l 在不同坐标轴下的表示图 首先说结论: 在复平面中,两个复数&a…...

为什么ta【给脸不要脸】:利他是一种选择,善良者的自我救赎与智慧策略
你满腔热忱,他却视而不见; 你伸出援手,他却恩将仇报; 你谦让包容,他却得寸进尺; 你善意提拔,他却并不领情,反而“给脸不要脸”。 所有人都曾被这种“好心当成驴肝肺”遭遇内耗&a…...

mysql 配置文件 my.cnf 增加 lower_case_table_names = 1 服务启动不了的原因
原因:在MySQL8.0之后的版本,只允许在数据库初始化时指定,之后不允许修改了 mysql 配置文件 my.cnf 增加 lower_case_table_names 1 服务启动不了 报错信息:Job for mysqld.service failed because the control process exited …...
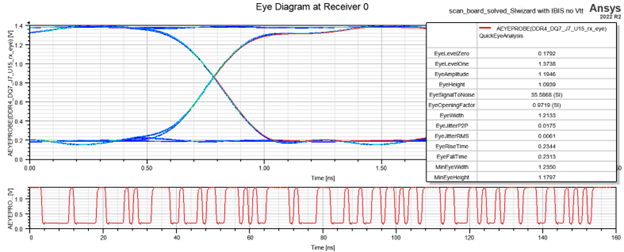
SIwave:释放 SIwizard 求解器的强大功能
SIwave 是一种电源完整性和信号完整性工具。SIwizard 是 SIwave 中 SI 分析的主要工具,也是本博客的主题。 SIwizard 用于研究 RF、clock 和 control traces 的信号完整性。该工具允许用户进行瞬态分析、眼图分析和 BER 计算。用户可以将 IBIS 和 IBIS-AMI 模型添加…...
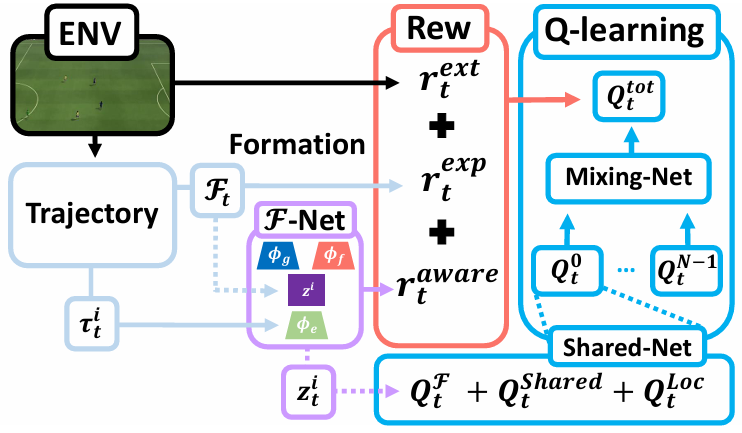
强化学习不愧“顶会收割机”!2大创新思路带你上大分,毕业不用愁!
强化学习之父Richard Sutton悄悄搞了个大的,提出了一个简单思路:奖励聚中。这思路简单效果却不简单,等于是给几乎所有的强化学习算法上了一个增强buff,所以这篇论文已经入选了首届强化学习会议(RLC 2024)&a…...

mac 修改启动图图标数量
调整每行显示图标数量: defaults write com.apple.dock springboard-rows -int 7 调整每列显示的数量 defaults write com.apple.dock springboard-columns -int 8 最后重置一下启动台 defaults write com.apple.dock ResetLaunchPad -bool TRUE;killall Dock 其…...

网站架构知识之Ansible进阶(day022)
1.handler触发器 应用场景:一般用于分发配置文件时候,如果配置文件有变化,则重启服务,如果没有变化,则不重启服务 案列01:分发nfs配置文件,若文件发生改变则重启服务 2.when判断 用于给ans运…...

VMware调整窗口为可以缩小但不改变显示内容的大小
也就是缩小窗口不会影响内容的大小 这样设置就好...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
