C++ 二叉搜索树(Binary Search Tree, BST)深度解析与全面指南:从基础概念到高级应用、算法优化及实战案例
🌟个人主页:落叶
🌟当前专栏: C++专栏
目录
⼆叉搜索树的概念
⼆叉搜索树的性能分析
⼆叉搜索树的插⼊
⼆叉搜索树的查找
二叉搜索树中序遍历
⼆叉搜索树的删除
cur的左节点为空的情况
cur的右节点为空的情况
左,右节点都不为空的情况
二叉搜索树【实现代码】
⼆叉搜索树key和key/value使⽤场景
key/value搜索场景
key/value⼆叉搜索树代码实现
⼆叉搜索树的概念
⼆叉搜索树⼜称⼆叉排序树,它或者是⼀棵空树,或者是具有以下性质的⼆叉树:
- 若它的左⼦树不为空,则左⼦树上所有结点的值都⼩于等于根结点的值
- 若它的右⼦树不为空,则右⼦树上所有结点的值都⼤于等于根结点的值
- 它的左右⼦树也分别为⼆叉搜索树
- ⼆叉搜索树中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,具体看使⽤场景定义,后续我 们学习map/set/multimap/multiset系列容器底层就是⼆叉搜索树,其中map/set不⽀持插⼊相等 值,multimap/multiset⽀持插⼊相等值

⼆叉搜索树的性能分析
最优情况下,⼆叉搜索树为完全⼆叉树(或者接近完全⼆叉树),其⾼度为: O(log2 N)

所以综合⽽⾔⼆叉搜索树增删查改时间复杂度为: O(N)
那么这样的效率显然是⽆法满⾜我们需求的,我们后续课程需要继续讲解⼆叉搜索树的变形,平衡⼆ 叉搜索树AVL树和红⿊树,才能适⽤于我们在内存中存储和搜索数据。
另外需要说明的是,⼆分查找也可以实现 O(logN) 级别的查找效率,但是⼆分查找有两⼤缺陷:
- 需要存储在⽀持下标随机访问的结构中,并且有序。
- 插⼊和删除数据效率很低,因为存储在下标随机访问的结构中,插⼊和删除数据⼀般需要挪动数 据。
这⾥也就体现出了平衡⼆叉搜索树的价值。

⼆叉搜索树的插⼊
插⼊的具体过程如下:
- 树为空,则直接新增结点,赋值给root指针
- 树不空,按⼆叉搜索树性质,插⼊值⽐当前结点⼤往右⾛,插⼊值⽐当前结点⼩往左⾛,找到空位 置,插⼊新结点。
- 如果⽀持插⼊相等的值,插⼊值跟当前结点相等的值可以往右⾛,也可以往左⾛,找到空位置,插 ⼊新结点。(要注意的是要保持逻辑⼀致性,插⼊相等的值不要⼀会往右⾛,⼀会往左⾛)
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};下面我们可以看到,要插入一个16节点,比8大往右边走,比10大往右走,比14大往右走,走到空了就可以插入16这个节点了。

下面我们要插入3这个节点,比8小往左边走, 如果和3允许冗余的情况下往后大的走。

当cur循环到空时候,就在这个位置插入3这个节点,还需要parent记录上一个节点,用来和3节点进行连接。

接下来创建节点,构造用于申请新节点后初始化

//定义根节点赋值为空

第一步:判断根节点是不是空,是空把节点给根节点。
第二步:循环等于空就停下来,key小于当前节点往左边走,大于就往右走。
第三步:new一块新节点数值是key的,key和parent比较,parent就是记录上一个节点,小于和左边连接,大于和右边连接。

//节点
template<class K>
struct BS_Node
{K _key;BS_Node<K>* _left;//左BS_Node<K>* _right;//右//构造-用于申请新节点后初始化BS_Node(const K& key):_key(key),_left(nullptr),_right(nullptr){}
};template<class K>
class BStree
{typedef BS_Node<K> Node;
public://插入bool insert(const K& key){//根节点为空if (_root == nullptr){//当前就给根节点_root = new Node(key);}//parent用于记录上一个节点,用来和新节点连接Node* parent = nullptr;Node* cur = _root;//循环到cur为空,就停下来while (cur != nullptr){//key小于当前节点往左边走if (key < cur->_key){//记录上一个节点parent = cur;cur = cur->_left;}//key大于当前节点往右边走else if(key > cur->_key){//记录上一个节点parent = cur;cur = cur->_right;}else{return true;}}//new一块新节点给curcur = new Node(key);if (key < parent->_key){//小于,和左边连接parent->_left = cur;}else{//大于,和右边连接parent->_right = cur;}return false;}private:Node* _root = nullptr;
};⼆叉搜索树的查找
- 从根开始⽐较,查找x,x⽐根的值⼤则往右边⾛查找,x⽐根值⼩则往左边⾛查找。
- 最多查找⾼度次,⾛到到空,还没找到,这个值不存在。
- 如果不⽀持插⼊相等的值,找到x即可返回
- 如果⽀持插⼊相等的值,意味着有多个x存在,⼀般要求查找中序的第⼀个x。如下图,查找3,要 找到1的右孩⼦的那个3返回

当我们要查询4从根节点开始,比8小往左边走,比3大往右边走,比6小往左走,找到4了,返回true。

.从根节点开始查询 ,cur不等于空,找到空了,就说明没有这个值。
小于当前节点往左边走,大于当前节点往右边走,等于就返回true。

二叉搜索树中序遍历
中序遍历定义在私有里,因为要从根节点开始遍历,需要用到根节点中序遍历。
然后在公有定义一个成员函数来,调用私有的中序遍历。

把数组的值插入到搜索二叉树,中序遍历打印出来。
因为没有9所以查询不到,返回false就是0。

⼆叉搜索树的删除
⾸先查找元素是否在⼆叉搜索树中,如果不存在,则返回false。
如果查找元素存在则分以下四种情况分别处理:(假设要删除的结点为N)
- 要删除结点N左右孩⼦均为空
- 要删除的结点N左孩⼦位空,右孩⼦结点不为空
- 要删除的结点N右孩⼦位空,左孩⼦结点不为空
- 要删除的结点N左右孩⼦结点均不为空
对应以上四种情况的解决⽅案:
- 把N结点的⽗亲对应孩⼦指针指向空,直接删除N结点(情况1可以当成2或者3处理,效果是⼀样 的)
- 把N结点的⽗亲对应孩⼦指针指向N的右孩⼦,直接删除N结点
- 把N结点的⽗亲对应孩⼦指针指向N的左孩⼦,直接删除N结点
- ⽆法直接删除N结点,因为N的两个孩⼦⽆处安放,只能⽤替换法删除。找N左⼦树的值最⼤结点 R(最右结点)或者N右⼦树的值最⼩结点R(最左结点)替代N,因为这两个结点中任意⼀个,放到N的 位置,都满⾜⼆叉搜索树的规则。替代N的意思就是N和R的两个结点的值交换,转⽽变成删除R结 点,R结点符合情况2或情况3,可以直接删除。
节点的删除,我们需要查询对应的节点,然后进行删除。

cur的左节点为空的情况
如果cur的左节点为空,那么parent这个父节点和cur的右节点进行连接。

如果要删除的节点是根节点,那么把_root这个根节点往右走,然后释放cur节点。

cur的右节点为空的情况
右节点为空,那么parent这个父节点和cur的左节点进行连接。

如果要删除的节点是根节点,那么把_root这个根节点往左走,然后释放cur节点。


左,右节点都不为空的情况
如果要删除3,需要右节点的最左的那个节点的数值拿来替换。
mincur是找cur右子树最小的那个节点,用来替换。
tab保存上一个节点,用来和mincur的右节点连接,如果右节点是空,那就是连接空节点。
把4的数值赋值给3这个节点,然后释放4这个节点。

如果要删除根节点,需要右节点的最左的那个节点的数值拿来替换。
我们发现10的左节点已经完成空了,那就是用10这个节点来替换了。

下面这个返回true,是查询到要删除的节点,就返回true.
找不到返回false.

二叉搜索树【实现代码】
Search for a binary tree.h【头文件】
#pragma once
#include<iostream>
using namespace std;namespace key
{//节点template<class K>struct BS_Node{K _key;BS_Node<K>* _left;//左BS_Node<K>* _right;//右//构造-用于申请新节点后初始化BS_Node(const K& key):_key(key), _left(nullptr), _right(nullptr){}};template<class K>class BStree{typedef BS_Node<K> Node;public://插入bool insert(const K& key){//根节点为空if (_root == nullptr){//当前就给根节点_root = new Node(key);}//parent用于记录上一个节点,用来和新节点连接Node* parent = nullptr;Node* cur = _root;//循环到cur为空,就停下来while (cur != nullptr){//key小于当前节点往左边走if (key < cur->_key){//记录上一个节点parent = cur;cur = cur->_left;}//key大于当前节点往右边走else if (key > cur->_key){//记录上一个节点parent = cur;cur = cur->_right;}else{return true;}}//new一块新节点给curcur = new Node(key);if (key < parent->_key){//小于,和左边连接parent->_left = cur;}else{//大于,和右边连接parent->_right = cur;}return false;}//查询bool find(const K& key){//从根节点开始查询Node* cur = _root;while (cur != nullptr){//小于当前节点,往左走if (key < cur->_key){cur = cur->_left;}//大于当前节点,往右走else if (key > cur->_key){cur = cur->_right;}else{return true;}}return false;}//删除bool Erase(const K& key){//查找Node* cur = _root;//parent用来记录上一个节点Node* parent = nullptr;while (cur != nullptr){if (key < cur->_key){//parent记录上一个节点parent = cur;cur = cur->_left;}else if (key > cur->_key){//parent记录上一个节点parent = cur;cur = cur->_right;}else//找到了进行删除{//当前节点的左节点为nullif (cur->_left == nullptr){//*****************************//要删除的节点等于根节点if (cur == _root){//让根节点往右走就行了_root = cur->_right;}//*****************************else{//父节点的左节点等于curif (parent->_left == cur){//cur节点的左节点为null,用cur的右节点和父节点连接parent->_left = cur->_right;}else{//cur节点的左节点为null,用cur的右节点和父节点连接parent->_right = cur->_right;}}delete cur;}//当前节点的右节点为nullelse if (cur->_right == nullptr){//*****************************//要删除的节点等于根节点if (cur == _root){//让根节点往右走就行了_root = cur->_left;}//*****************************else{//父节点的左节点等于curif (parent->_left == cur){//cur节点的右节点为null,用cur的左节点和父节点连接parent->_left = cur->_left;}else{//cur节点的右节点为null,用cur的左节点和父节点连接parent->_right = cur->_left;}}delete cur;}else//左,右都不为空的情况{//找右子树最小的节点(最左)替代我的位置//保存cur的右节点Node* mincur = cur->_right;//这个给cur,解决没有就循环就没有刷新的问题Node* tab = cur;while (mincur->_left != nullptr){//保存上一个节点tab = mincur;//一直往左边节点走,mincur = mincur->_left;}//一直往左边节点走,找到最小的那个,赋值给curcur->_key = mincur->_key;//删除的节点为根节点,右节点为mincurif (tab->_right == mincur){//tab右节点和mincur右节点进行连接tab->_right = mincur->_right;}else //左节点为mincur{//tab的左边,和mincur的右边进行连接tab->_left = mincur->_right;}delete mincur;}return true;}}return false;}//用来调用中序遍历void InOrder(){_InOrder(_root);cout << endl;}private://中序遍历void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;};
}
test.cpp【测试】
#include"Search for a binary tree.h"int main()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };key::BStree<int> t;for (auto i : a){t.insert(i);}t.InOrder();cout << t.find(9) << endl;for (auto i : a){t.Erase(i);t.InOrder();}}⼆叉搜索树key和key/value使⽤场景
只有key作为关键码,结构中只需要存储key即可,关键码即为需要搜索到的值,搜索场景只需要判断 key在不在。key的搜索场景实现的⼆叉树搜索树⽀持增删查,但是不⽀持修改,修改key破坏搜索树结 构了。
场景1:⼩区⽆⼈值守⻋库,⼩区⻋库买了⻋位的业主⻋才能进⼩区,那么物业会把买了⻋位的业主的 ⻋牌号录⼊后台系统,⻋辆进⼊时扫描⻋牌在不在系统中,在则抬杆,不在则提⽰⾮本⼩区⻋辆,⽆ 法进⼊。
场景2:检查⼀篇英⽂⽂章单词拼写是否正确,将词库中所有单词放⼊⼆叉搜索树,读取⽂章中的单 词,查找是否在⼆叉搜索树中,不在则波浪线标红提⽰。

key/value搜索场景
每⼀个关键码key,都有与之对应的值value,value可以任意类型对象。树的结构中(结点)除了需要存 储key还要存储对应的value,增/删/查还是以key为关键字⾛⼆叉搜索树的规则进⾏⽐较,可以快速查 找到key对应的value。key/value的搜索场景实现的⼆叉树搜索树⽀持修改,但是不⽀持修改key,修 改key破坏搜索树结构了,可以修改value。
场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时 查找到了英⽂对应的中⽂。
场景2:商场⽆⼈值守⻋库,⼊⼝进场时扫描⻋牌,记录⻋牌和⼊场时间,出⼝离场时,扫描⻋牌,查 找⼊场时间,⽤当前时间-⼊场时间计算出停⻋时⻓,计算出停⻋费⽤,缴费后抬杆,⻋辆离场。
场景3:统计⼀篇⽂章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第⼀次 出现,(单词,1),单词存在,则++单词对应的次数。

key/value⼆叉搜索树代码实现
Search for a binary tree.h
#pragma once
#include<iostream>
using namespace std;namespace key
{//节点template<class K,class V>struct BS_Node{K _key;V _val;BS_Node<K,V>* _left;//左BS_Node<K,V>* _right;//右//构造-用于申请新节点后初始化BS_Node(const K& key,const V& val):_key(key),_val(val), _left(nullptr), _right(nullptr){}};template<class K,class V>class BStree{typedef BS_Node<K,V> Node;public://插入bool insert(const K& key,const V&val){//根节点为空if (_root == nullptr){//当前就给根节点_root = new Node(key,val);}//parent用于记录上一个节点,用来和新节点连接Node* parent = nullptr;Node* cur = _root;//循环到cur为空,就停下来while (cur != nullptr){//key小于当前节点往左边走if (key < cur->_key){//记录上一个节点parent = cur;cur = cur->_left;}//key大于当前节点往右边走else if (key > cur->_key){//记录上一个节点parent = cur;cur = cur->_right;}else{return false;}}//new一块新节点给curcur = new Node(key,val);if (key < parent->_key){//小于,和左边连接parent->_left = cur;}else{//大于,和右边连接parent->_right = cur;}return true;}//查询Node* find(const K& key){//从根节点开始查询Node* cur = _root;while (cur != nullptr){//小于当前节点,往左走if (key < cur->_key){cur = cur->_left;}//大于当前节点,往右走else if (key > cur->_key){cur = cur->_right;}else{//找到了返回当前节点return cur;}}//找不到返回空return nullptr;}//删除bool Erase(const K& key){//查找Node* cur = _root;//parent用来记录上一个节点Node* parent = nullptr;while (cur != nullptr){if (key < cur->_key){//parent记录上一个节点parent = cur;cur = cur->_left;}else if (key > cur->_key){//parent记录上一个节点parent = cur;cur = cur->_right;}else//找到了进行删除{//当前节点的左节点为nullif (cur->_left == nullptr){//*****************************//要删除的节点等于根节点if (cur == _root){//让根节点往右走就行了_root = cur->_right;}//*****************************else{//父节点的左节点等于curif (parent->_left == cur){//cur节点的左节点为null,用cur的右节点和父节点连接parent->_left = cur->_right;}else{//cur节点的左节点为null,用cur的右节点和父节点连接parent->_right = cur->_right;}}delete cur;}//当前节点的右节点为nullelse if (cur->_right == nullptr){//*****************************//要删除的节点等于根节点if (cur == _root){//让根节点往右走就行了_root = cur->_left;}//*****************************else{//父节点的左节点等于curif (parent->_left == cur){//cur节点的右节点为null,用cur的左节点和父节点连接parent->_left = cur->_left;}else{//cur节点的右节点为null,用cur的左节点和父节点连接parent->_right = cur->_left;}}delete cur;}else//左,右都不为空的情况{//找右子树最小的节点(最左)替代我的位置//保存cur的右节点Node* mincur = cur->_right;//这个给cur,解决没有就循环就没有刷新的问题Node* tab = cur;while (mincur->_left != nullptr){//保存上一个节点tab = mincur;//一直往左边节点走,mincur = mincur->_left;}//一直往左边节点走,找到最小的那个,赋值给curcur->_key = mincur->_key;//删除的节点为根节点,右节点为mincurif (tab->_right == mincur){//tab右节点和mincur右节点进行连接tab->_right = mincur->_right;}else //左节点为mincur{//tab的左边,和mincur的右边进行连接tab->_left = mincur->_right;}delete mincur;}return true;}}return false;}//用来调用中序遍历void InOrder(){_InOrder(_root);cout << endl;}private://中序遍历void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " " <<_root->_val <<endl;_InOrder(root->_right);}Node* _root = nullptr;};
}
test.cpp
int main()
{string arr[] = { "苹果","香蕉","香蕉","西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "香蕉","香蕉","香蕉" };key::BStree<string, int> countTree;for (auto& e : arr){//key_value::BSTNode<string, int>* ret = countTree.Find(e);auto ret = countTree.find(e);if (ret == nullptr){countTree.insert(e, 1);}else{ret->_val++;}}countTree.InOrder();return 0;
}场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时 查找到了英⽂对应的中⽂。
//int main()
//{
// key::BStree<string, string> dict;
// //BSTree<string, string> copy = dict;
// dict.insert("left", "左边");
// dict.insert("right", "右边");
// dict.insert("insert", "插⼊");
// dict.insert("string", "字符串");
// string str;
// while (cin >> str)
// {
// auto ret = dict.find(str);
// if (ret)
// {
// cout << "->" << ret->_val << endl;
// }
// else
// {
// cout << "⽆此单词,请重新输⼊" << endl;
// }
// }
// return 0;
//}相关文章:

C++ 二叉搜索树(Binary Search Tree, BST)深度解析与全面指南:从基础概念到高级应用、算法优化及实战案例
🌟个人主页:落叶 🌟当前专栏: C专栏 目录 ⼆叉搜索树的概念 ⼆叉搜索树的性能分析 ⼆叉搜索树的插⼊ ⼆叉搜索树的查找 二叉搜索树中序遍历 ⼆叉搜索树的删除 cur的左节点为空的情况 cur的右节点为空的情况 左,右节点都不为…...

刷题日常(移动零,盛最多水的容器,三数之和,无重复字符的最长子串)
移动零 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。 请注意 ,必须在不复制数组的情况下原地对数组进行操作。 俩种情况: 1.当nums[i]为0的时候 直接i 2.当nums[i]不为0的时候 此时 …...

深入了解决策树---机器学习中的经典算法
引言 决策树(Decision Tree)是一种重要的机器学习模型,以直观的分层决策方式和简单高效的特点成为分类和回归任务中广泛应用的工具。作为解释性和透明性强的算法,决策树不仅适用于小规模数据,也可作为复杂模型的基石&…...

Elasticsearch对于大数据量(上亿量级)的聚合如何实现?
大家好,我是锋哥。今天分享关于【Elasticsearch对于大数据量(上亿量级)的聚合如何实现?】面试题。希望对大家有帮助; Elasticsearch对于大数据量(上亿量级)的聚合如何实现? 1000道 …...

深度学习模型:循环神经网络(RNN)
一、引言 在深度学习的浩瀚海洋里,循环神经网络(RNN)宛如一颗独特的明珠,专门用于剖析序列数据,如文本、语音、时间序列等。无论是预测股票走势,还是理解自然语言,RNN 都发挥着举足轻重的作用。…...

前端---HTML(一)
HTML_网络的三大基石和html普通文本标签 1.我们要访问网络,需不需要知道,网络上的东西在哪? 为什么我们写,www.baidu.com就能找到百度了呢? 我一拼ping www.baidu.com 就拼到了ip地址: [119.75.218.70]…...

SQL 复杂查询
目录 复杂查询 一、目的和要求 二、实验内容 (1)查询出所有水果产品的类别及详情。 查询出编号为“00000001”的消费者用户的姓名及其所下订单。(分别采用子查询和连接方式实现) 查询出每个订单的消费者姓名及联系方式。 在…...

银河麒麟桌面系统——桌面鼠标变成x,窗口无关闭按钮的解决办法
银河麒麟桌面系统——桌面鼠标变成x,窗口无关闭按钮的解决办法 1、支持环境2、详细操作说明步骤1:用root账户登录电脑步骤2:导航到kylin-wm-chooser目录步骤3:编辑default.conf文件步骤4:重启电脑 3、结语 Ὁ…...

抓包之使用chrome的network面板
写在前面 本文看下工作中非常非常常用的chrome的network面板功能。 官方介绍:地址。 1:前置 1.1:打开 右键-》检查,或者F12。 1.2:组成部分 2:控制器常用功能 详细如下图: 接着我们挑选其…...

避坑ffmpeg直接获取视频fps不准确
最近在做视频相关的任务,调试代码发现一个非常坑的点,就是直接用ffmpeg获取fps是有很大误差的,如下: # GPT4o generated import ffmpegprobe ffmpeg.probe(video_path, v"error", select_streams"v:0", sho…...

大数据新视界 -- 大数据大厂之 Hive 函数库:丰富函数助力数据处理(上)(11/ 30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

深入解析 Django 中数据删除的最佳实践:以动态管理镜像版本为例
文章目录 引言场景与模型设计场景描述 删除操作详解1. 删除单个 Tag2. 批量删除 Tags3. 删除前确认4. 日志记录 高阶优化与问题分析1. 外键约束与误删保护2. 并发删除的冲突处理3. 使用软删除 结合 Django Admin 的实现总结与实践思考 引言 在现代应用开发中,服务和…...

【java】sdkman-java多环境切换工具
#java #env #sdk #lcshand 首先我们来复习一下,可参考我原来的文章: python多个版本的切换可用pyenv nodejs多个版本的切换可用nvm 同样,java多个版本的切换可用sdkman和jenv,我偏重于使用sdkman,因为有时候我也需要…...

11.25c++继承、多态
练习: 编写一个 武器类 class Weapon{int atk; }编写3个武器派生类:短剑,斧头,长剑 class knife{int spd; }class axe{int hp; }class sword{int def; }编写一个英雄类 class Hero{int atk;int def;int spd;int hp; public:所有的…...
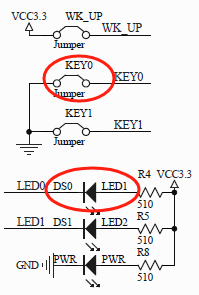
STM32F103外部中断配置
一、外部中断 在上一节我们介绍了STM32f103的嵌套向量中断控制器,其中包括中断的使能、失能、中断优先级分组以及中断优先级配置等内容。 1.1 外部中断/事件控制器 在STM32f103支持的60个可屏蔽中断中,有一些比较特殊的中断: 中断编号13 EXTI…...

阿里电商大整合,驶向价值竞争新航道
阿里一出手就是王炸。11月21日,阿里公布了最新动作:将国内和海外电商业务整合,成立新的电商事业群。这是阿里首次将所有电商业务整合到一起,也对电商行业未来发展有着借鉴意义。阿里为何要这么干?未来又将给行业带来哪…...

等保测评在云计算方面的应用讲解
等保测评(信息安全等级保护测评)在云计算方面的应用主要聚焦于如何满足等级保护相关要求,并确保云计算平台及其上运行的业务系统的安全性。以下是主要内容的讲解: 1. 云计算中的等保测评概述 等保测评是在我国网络安全等级保护制…...
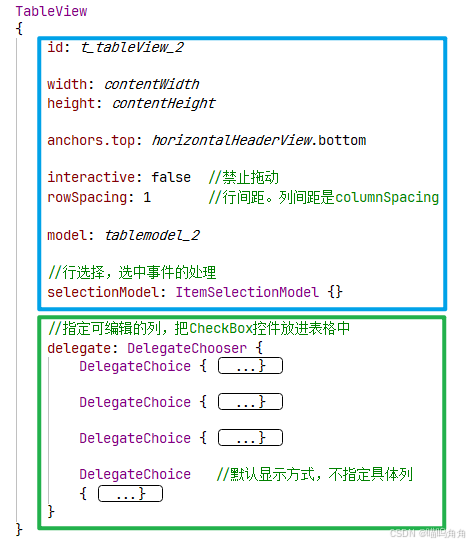
QML TableView 实例演示 + 可能遇到的一些问题(Qt_6_5_3)
一、可能遇到的一些问题 Q1:如何禁用拖动? 在TableView下加一句代码即可: interactive: false 补充:这个属性并不专属于TableView,而是一个通用属性。很多Controls下的控件都可以使用,其主要作用就是控…...
SpringBoot集成RabbitMQ实现流量削峰添谷)
SpringBoot(三十九)SpringBoot集成RabbitMQ实现流量削峰添谷
前边我们有具体的学习过RabbitMQ的安装和基本使用的情况。 但是呢,没有演示具体应用到项目中的实例。 这里使用RabbitMQ来实现流量的削峰添谷。 一:添加pom依赖 <!--rabbitmq-需要的 AMQP 依赖--> <dependency><groupId>org.springfr…...

前端 Vue 3 后端 Node.js 和Express 结合cursor常见提示词结构
cursor 提示词 后端提示词 请为我开发一个基于 Node.js 和Express 框架的 Todo List 后端项目。项目需要实现以下四个 RESTful API 接口: 查询所有待办事项 接口名: GET /api/get-todo功能: 从数据库的’list’集合中查询并返回所有待办事项参数: 无返回: 包含所…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

