【王道数据结构】第八章 | 排序
目录
8.1. 排序的基本概念
8.2. 插入排序
8.2.1. 直接插入排序
8.2.2. 折半插入排序
8.2.3. 希尔排序
8.3. 交换排序
8.3.1. 冒泡排序
8.3.2. 快速排序
8.4. 选择排序
8.4.1. 简单选择排序
8.4.2. 堆排序
8.5. 归并排序和基数排序
8.5.2. 基数排序
8.1. 排序的基本概念

- 排序:重新排列表中的元素,使表中元素满足按关键字有序的过程。
- 输入:n个记录
,对应的关键字为
。
- 输出::输入序列的一个重排
,使得
。
- 算法的稳定性:若待排序表中有两个元素
和
,其对应的关键字相同即
=
,且在排序前
在
的前面,若使用某一排序算法排序后,
仍然在
的前面,则称这个排序算法是稳定的,否则称排序算法是不稳定的。
- 排序算法的评价指标:时间复杂度、空间复杂度、稳定性。
- 排序算法的分类:
内部排序: 排序期间元素都在内存中——关注如何使时间、空间复杂度更低。
外部排序: 排序期间元素无法全部同时存在内存中,必须在排序的过程中根据要求不断地在内、外存之间移动——关注如何使时间、空间复杂度更低,如何使读/写磁盘次数更少。
- 排序算法的分类:
8.2. 插入排序

8.2.1. 直接插入排序
- 算法思想:每次将一个待排序的记录按其关键字大小,插入到前面已经排好序的子序列中,直到全部记录插入完成。
代码实现(不带哨兵):
// 对A[]数组中共n个元素进行插入排序
void InsertSort(int A[],int n){int i,j,temp;for(i=1; i<n; i++){if(A[i]<A[i-1]){ //如果A[i]关键字小于前驱temp=A[i]; for(j=i-1; j>=0 && A[j]>temp; --j)A[j+1]=A[j]; //所有大于temp的元素都向后挪A[j+1]=temp;}}
}
代码实现(带哨兵):
// 对A[]数组中共n个元素进行插入排序
void InsertSort(int A[], int n){int i,j;for(i=2; i<=n; i++){if(A[i]<A[i-1]){A[0]=A[i]; //复制为哨兵,A[0]不放元素for(j=i-1; A[0]<A[j]; --j)A[j+1]=A[j];A[j+1]=A[0];}}
}
- 算法效率分析:
- 时间复杂度:最好情况 O(n),最差情况O(
),平均情况 O(
)。
- 空间复杂度:O(1)。
- 算法稳定性:稳定。
- 适用性:适用于顺序存储和链式存储的线性表。
- 时间复杂度:最好情况 O(n),最差情况O(
对链表进行插入排序代码实现:
//对链表L进行插入排序
void InsertSort(LinkList &L){LNode *p=L->next, *pre;LNode *r=p->next;p->next=NULL;p=r;while(p!=NULL){r=p->next;pre=L;while(pre->next!=NULL && pre->next->data<p->data)pre=pre->next;p->next=pre->next;pre->next=p;p=r;}
}
8.2.2. 折半插入排序
- 算法思路: 每次将一个待排序的记录按其关键字大小,使用折半查找找到前面子序列中应该插入的位置并插入,直到全部记录插入完成。
- 注意:为了保证稳定性,当查找到和插入元素关键字一样的元素时,应该在这个元素的右半部分继续查找以确认位置。即当 A[mid] == A[0] 时,应继续在mid所指位置右边寻找插入位置。
代码实现:
//对A[]数组中共n个元素进行折半插入排序
void InsertSort(int A[], int n){ int i,j,low,high,mid;for(i=2; i<=n; i++){A[0]=A[i]; //将A[i]暂存到A[0]low=1; high=i-1;while(low<=high){ //折半查找mid=(low+high)/2;if(A[mid]>A[0])high=mid-1;elselow=mid+1;}for(j=i-1; j>high+1; --j)A[j+1]=A[j];A[high+1]=A[0];}
}
- 与直接插入排序相比,比较关键字的次数减少了,但是移动元素的次数没有变。时间复杂度仍为 O(n²)。
8.2.3. 希尔排序
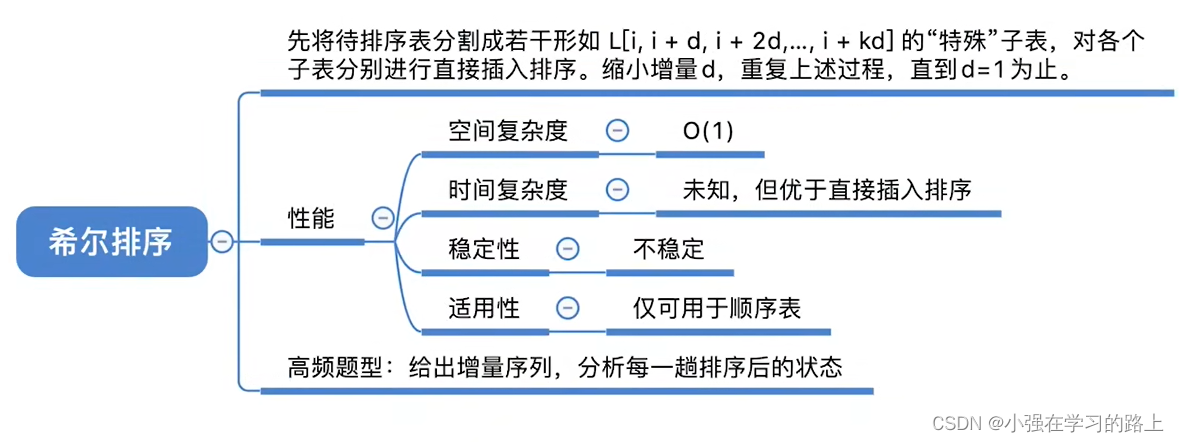
- 算法思路:先追求表中元素的部分有序,再逐渐逼近全局有序,以减小插入排序算法的时间复杂度。
- 具体实施:希尔排序:先将待排序表分割成若干形如
的“特殊”子表,对各个子表分别进行直接插入排序。缩小增量d,重复上述过程,直到d=1为止。
希尔排序代码实现:
// 对A[]数组共n个元素进行希尔排序
void ShellSort(ElemType A[], int n){int d,i,j;for(d=n/2; d>=1; d=d/2){ //步长d递减for(i=d+1; i<=n; ++i){if(A[i]<A[i-d]){A[0]=A[i]; //A[0]做暂存单元,不是哨兵for(j=i-d; j>0 && A[0]<A[j]; j-=d)A[j+d]=A[j];A[j+d]=A[0];}}}
}
- 算法效率分析:
- 时间复杂度:希尔排序时间复杂度依赖于增量序列的函数。最差情况O(
),n在某个特顶范围时可达O(
) 。
- 空间复杂度:O(1)
- 算法稳定性:不稳定。
- 时间复杂度:希尔排序时间复杂度依赖于增量序列的函数。最差情况O(
8.3. 交换排序
8.3.1. 冒泡排序

- 算法思路:从后往前(或从前往后)两两比较相邻元素的值,若为逆序(即 A [ i − 1 ] > A [ i ]) ,则交换它们,直到序列比较完。如此重复最多 n-1 次冒泡就能将所有元素排好序。为保证稳定性,关键字相同的元素不交换。
冒泡排序代码实现:
// 交换a和b的值
void swap(int &a, int &b){int temp=a;a=b;b=temp;
}// 对A[]数组共n个元素进行冒泡排序
void BubbleSort(int A[], int n){for(int i=0; i<n-1; i++){bool flag = false; //标识本趟冒泡是否发生交换for(int j=n-1; j>i; j--){if(A[j-1]>A[j]){swap(A[j-1],A[j]);flag=true;}}if(flag==false)return; //若本趟遍历没有发生交换,说明已经有序}
}
- 算法效率分析:
- 时间复杂度:最好情况O(n) ,最差情况O(
),平均情况O(
)。
- 空间复杂度:O(1)。
- 稳定性:稳定。
- 适用性:冒泡排序可以用于顺序表、链表。
- 时间复杂度:最好情况O(n) ,最差情况O(
8.3.2. 快速排序
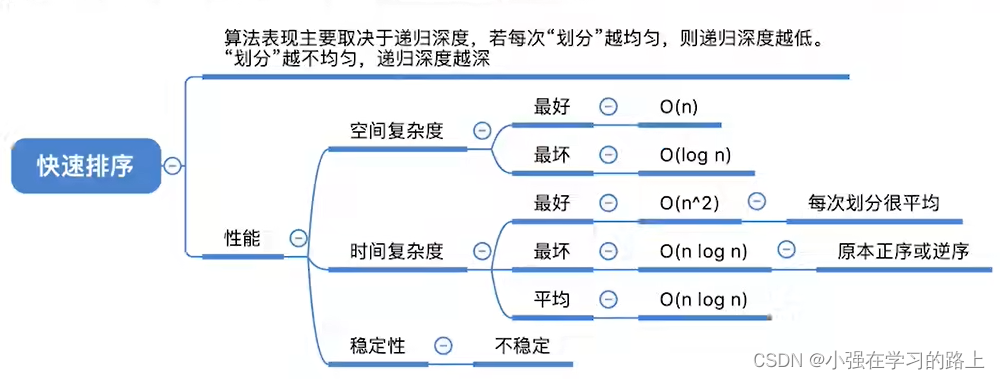
- 算法思路:在待排序表 L [ 1... n ] 中任选一个元素 pivot 作为枢轴(通常取首元素),通过一趟排序将待排序表分为独立的两部分 L [ 1... k − 1 ] 和 L [ k − 1... n ] 。使得 L [ 1... k − 1 ] 中的所有元素小于 pivot,L [ k − 1... n ]中的所有元素大于等于 pivot,则 pivot 放在了其最终位置 L [ k ]上。重复此过程直到每部分内只有一个元素或空为止。
- 快速排序是所有内部排序算法中性能最优的排序算法。
- 在快速排序算法中每一趟都会将枢轴元素放到其最终位置上。(可用来判断进行了几趟快速排序)
- 快速排序可以看作数组中n个元素组织成二叉树,每趟处理的枢轴是二叉树的根节点,递归调用的层数是二叉树的层数。
快速排序代码实现:
// 用第一个元素将数组A[]划分为两个部分
int Partition(int A[], int low, int high){int pivot = A[low];while(low<high){while(low<high && A[high]>=pivot)--high;A[low] = A[high];while(low<high && A[low]<=pivot) ++low;A[high] = A[low];}A[low] = pivot;return low;
} // 对A[]数组的low到high进行快速排序
void QuickSort(int A[], int low, int high){if(low<high){int pivotpos = Partition(A, low, high); //划分QuickSort(A, low, pivotpos - 1);QuickSort(A, pivotpos + 1, high);}
}
- 算法效率分析:
- 时间复杂度:快速排序的时间复杂度 = O ( n × 递 归 调 用 的 层 数 ) 。最好情况 O(
),最差情况 O(
) ,平均情况O(
)。
- 空间复杂度:快速排序的空间复杂度 = O ( 递 归 调 用 的 层 数 ) O(递归调用的层数)O(递归调用的层数)。最好情况O(
),最差情况 O(n),平均情况 O(
)。
- 时间复杂度:快速排序的时间复杂度 = O ( n × 递 归 调 用 的 层 数 ) 。最好情况 O(
8.4. 选择排序
- 选择排序思想: 每一趟在待排序元素中选取关键字最小(或最大)的元素加入有序子序列。
8.4.1. 简单选择排序
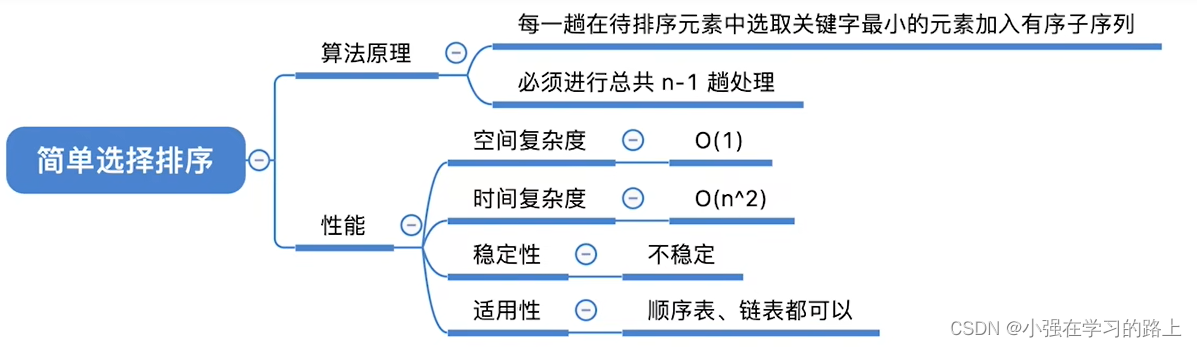
- 算法思路:每一趟在待排序元素中选取关键字最小的元素与待排序元素中的第一个元素交换位置。
简单选择排序代码实现:
// 交换a和b的值
void swap(int &a, int &b){int temp = a;a = b;b = temp;
}// 对A[]数组共n个元素进行选择排序
void SelectSort(int A[], int n){for(int i=0; i<n-1; i++){ //一共进行n-1趟,i指向待排序序列中第一个元素int min = i;for(int j=i+1; j<n; j++){ //在A[i...n-1]中选择最小的元素if(A[j]<A[min])min = j;}if(min!=i) swap(A[i], A[min]);}
}
- 算法效率分析:
- 时间复杂度:无论待排序序列有序、逆序还是乱序,都需要进行 n-1 次处理,总共需要对比关键字(n−1)+(n−2)+. . .+1=n( n−1) /2 次,因此时间复杂度始终是O(
) 。
- 空间复杂度:O(1) 。
- 稳定性:不稳定。
- 适用性:适用于顺序存储和链式存储的线性表。
- 时间复杂度:无论待排序序列有序、逆序还是乱序,都需要进行 n-1 次处理,总共需要对比关键字(n−1)+(n−2)+. . .+1=n( n−1) /2 次,因此时间复杂度始终是O(
对链表进行简单选择排序:
void selectSort(LinkList &L){LNode *h=L,*p,*q,*r,*s;L=NULL;while(h!=NULL){p=s=h; q=r=NULL;while(p!=NULL){if(p->data>s->data){s=p; r=q;}q=p; p=p->next;}if(s==h)h=h->next;elser->next=s->next;s->next=L; L=s;}
}
8.4.2. 堆排序
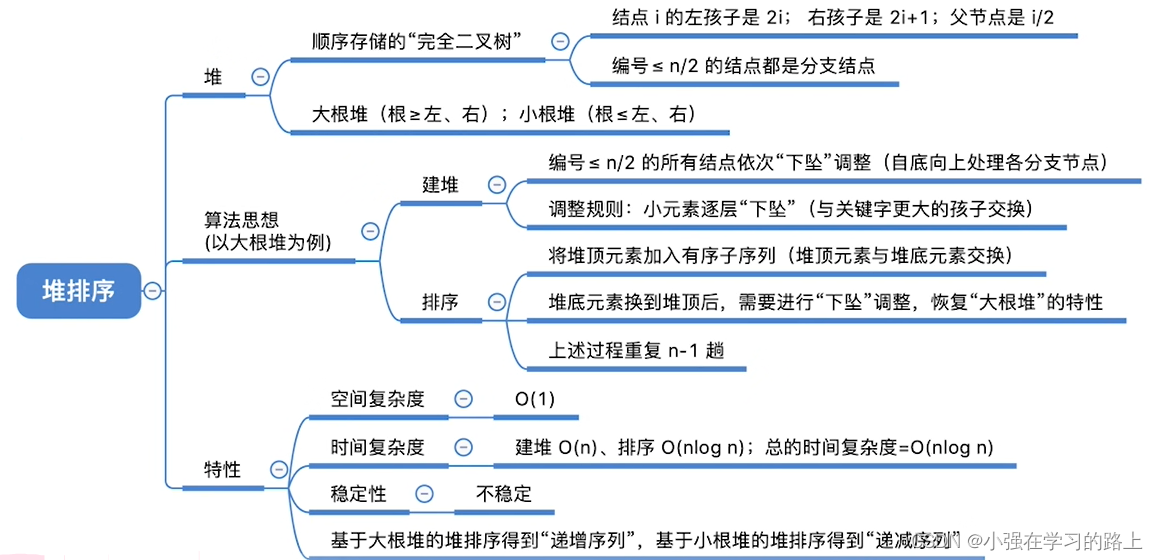
- 算法思路:首先将存放在 L [ 1... n ] 中的n个元素建成初始堆,由于堆本身的特点,堆顶元素就是最大值。将堆顶元素与堆底元素交换,这样待排序列的最大元素已经找到了排序后的位置。此时剩下的元素已不满足大根堆的性质,堆被破坏,将堆顶元素下坠使其继续保持大根堆的性质,如此重复直到堆中仅剩一个元素为止。
- 在顺序存储的完全二叉树中:
- 非终端结点的编号 :i ≤ [ n / 2 ]
- i 的左右孩子 :2i 和 2i+1
- i 的父节点:[ i / 2 ]
堆排序代码实现:
// 对初始序列建立大根堆
void BuildMaxHeap(int A[], int len){for(int i=len/2; i>0; i--) //从后往前调整所有非终端结点HeadAdjust(A, i, len);
}// 将以k为根的子树调整为大根堆
void HeadAdjust(int A[], int k, int len){A[0] = A[k];for(int i=2*k; i<=len; i*=2){ //沿k较大的子结点向下调整if(i<len && A[i]<A[i+1]) i++;if(A[0] >= A[i])break;else{A[k] = A[i]; //将A[i]调整至双亲结点上k=i; //修改k值,以便继续向下筛选}}A[k] = A[0]
}// 交换a和b的值
void swap(int &a, int &b){int temp = a;a = b;b = temp;
}// 对长为len的数组A[]进行堆排序
void HeapSort(int A[], int len){BuildMaxHeap(A, len); //初始建立大根堆for(int i=len; i>1; i--){ //n-1趟的交换和建堆过程swap(A[i], A[1]);HeadAdjust(A,1,i-1);}
}
- 算法效率分析:
- 时间复杂度:O(
)。建堆时间 O(n) ,之后进行 n-1 次向下调整操作,每次调整时间复杂度为O(
)。
- 空间复杂度:O(1)。
- 稳定性:不稳定。
- 时间复杂度:O(
-
堆的插入:对于大(或小)根堆,要插入的元素放到表尾,然后与父节点对比,若新元素比父节点更大(或小),则将二者互换。新元素就这样一路==“上升”==,直到无法继续上升为止。
-
堆的删除:被删除的元素用堆底元素替换,然后让该元素不断==“下坠”==,直到无法下坠为止。
8.5. 归并排序和基数排序
- 归并(Merge):把两个或多个已经有序的序列合并成一个新的有序表。k路归并每选出一个元素,需对比关键字k-1次。
- 算法思想:把待排序表看作 n 个有序的长度为1的子表,然后两两合并,得到 ⌈ n / 2 ⌉ 个长度为2或1的有序表……如此重复直到合并成一个长度为n的有序表为止。
代码实现:
// 辅助数组B
int *B=(int *)malloc(n*sizeof(int));// A[low,...,mid],A[mid+1,...,high]各自有序,将这两个部分归并
void Merge(int A[], int low, int mid, int high){int i,j,k;for(k=low; k<=high; k++)B[k]=A[k];for(i=low, j=mid+1, k=i; i<=mid && j<= high; k++){if(B[i]<=B[j])A[k]=B[i++];elseA[k]=B[j++];}while(i<=mid)A[k++]=B[i++];while(j<=high) A[k++]=B[j++];
}// 递归操作
void MergeSort(int A[], int low, int high){if(low<high){int mid = (low+high)/2;MergeSort(A, low, mid);MergeSort(A, mid+1, high);Merge(A,low,mid,high); //归并}
}
8.5.2. 基数排序
- 算法思想:把整个关键字拆分为d位,按照各个关键字位递增的次序(比如:个、十、百),做d趟“分配”和“收集”,若当前处理关键字位可能取得r个值,则需要建立r个队列。
- 分配:顺序扫描各个元素,根据当前处理的关键字位,将元素插入相应的队列。一趟分配耗时O ( n ) O(n)O(n)。
- 收集:把各个队列中的结点依次出队并链接。一趟收集耗时O ( r ) O(r)O(r)。
- 基数排序擅长处理的问题:
- 数据元素的关键字可以方便地拆分为d组,且d较小。
- 每组关键字的取值范围不大,即r较小。
- 数据元素个数n较大。
- 算法效率分析:算法效率分析:
- 时间复杂度:一共进行d趟分配收集,一趟分配需要 O ( n ),一趟收集需要 O(r) ,时间复杂度为 O[ d ( n + r ) ] ,且与序列的初始状态无关.
- 空间复杂度:O(r),其中r为辅助队列数量。
- 稳定性:稳定。
未完待续
相关文章:
【王道数据结构】第八章 | 排序
目录 8.1. 排序的基本概念 8.2. 插入排序 8.2.1. 直接插入排序 8.2.2. 折半插入排序 8.2.3. 希尔排序 8.3. 交换排序 8.3.1. 冒泡排序 8.3.2. 快速排序 8.4. 选择排序 8.4.1. 简单选择排序 8.4.2. 堆排序 8.5. 归并排序和基数排序 8.5.2. 基数排序 8.1. 排序的基本概念 排…...
95后外贸SOHO,年入7位数,他究竟是怎么做的?
外贸SOHO,一年到底能挣多少钱?有人说:“勤勤恳恳,年薪也就十来万吧”;也有人说:“100万而已我早就已经挣到了”;还有人说:“谁说新手难出头?我做跨境半年赚200万…...
2023年全国最新消防设施操作员精选真题及答案
百分百题库提供消防设施操作员考试试题、消防设施操作员考试预测题、消防设施操作员考试真题、消防设施操作员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 一、多选题 15、以下符合电气火灾监控系统监控设备的安装要求的有:( ) A、…...

mysql 无需修改配置文件,即可改变表数据存储位置
由于Linux系统的mysql 默认数据存储在/var/lib/mysql路径下,而该路径装系统时默认大小仅50G,当我们的数据稍微大一点时就会把该空间占满,无法再插入数据。 针对该问题有两种解决办法: 1、修改/etc/my.cnf配置文件,重启…...

轻松解决Session-Cookie 鉴权(含坑)附代码
Session-Cookie 鉴权 cookie介绍 Cookie 存储在客户端,可随意篡改,不安全有大小限制,最大为 4kb有数量限制,一般一个浏览器对于一个网站只能存不超过 20 个 Cookie,浏览器一般只允许存放 300个 CookieCookie 是不可跨…...

pyinstaller使用详细
目录常用命令spec文件配置报错常用命令 pyinstaller -D xxx.py //打包生成目录(director)pyinstaller -F xxx.py//打包生成单个exe文件pyinstaller xxx.spec //根据现有的spec文件进行打包运行以上命令之一后会生成build、dist文件夹以及xxx.spec文件&a…...
java -数据结构,List相关基础知识,ArrayList的基本使用,泛型的简单、包装类介绍
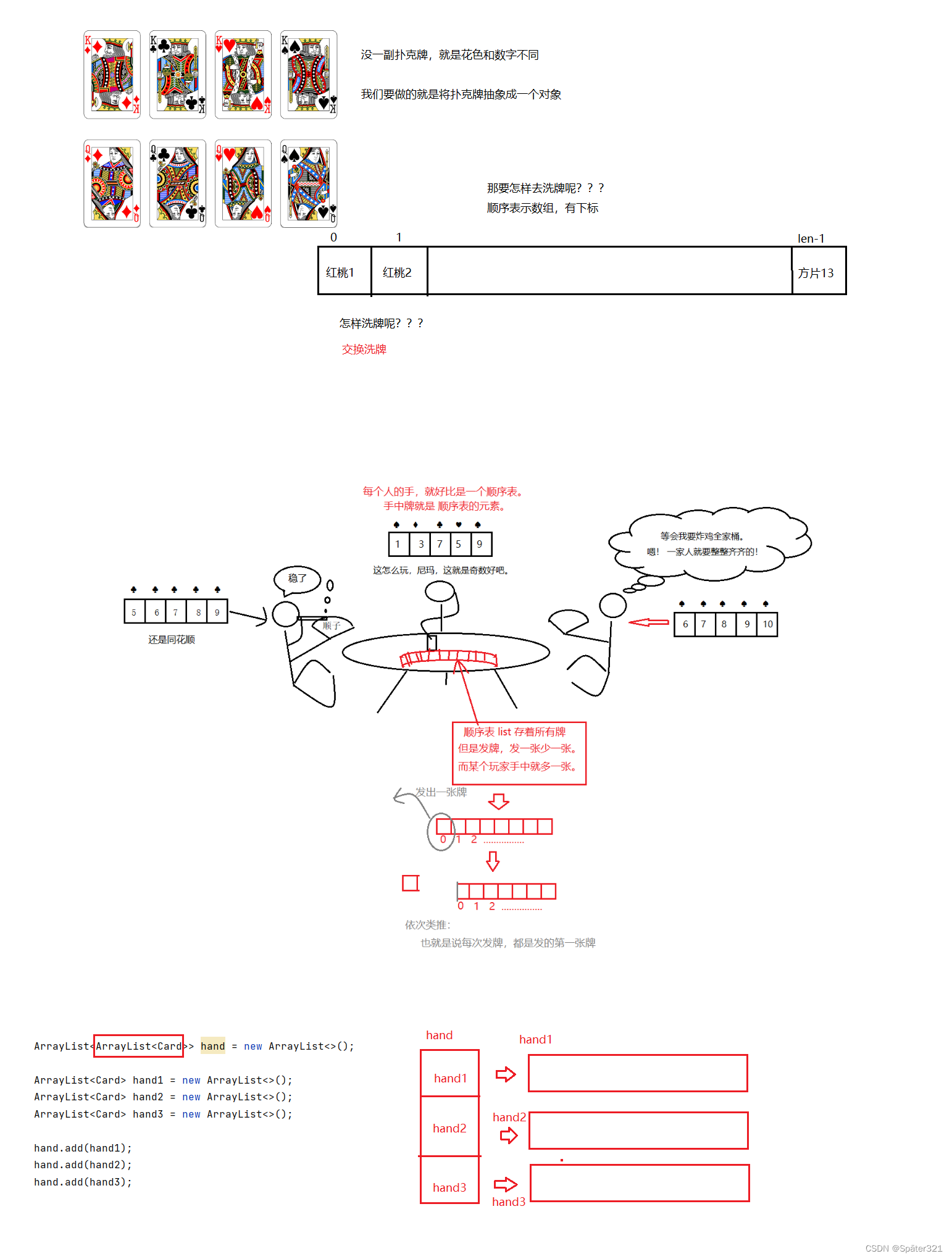
一、 预备知识-泛型(Generic) 1.1、泛型的引入 比如:我们实现一个简单的顺序表 class MyArrayList{public int[] elem;public int usedSize;public MyArrayList(){this.elem new int[10];}public void add(int key){this.elem[usedSize] key;usedSize;}public …...
RabbitMQ学习总结(10)—— RabbitMQ如何保证消息的可靠性
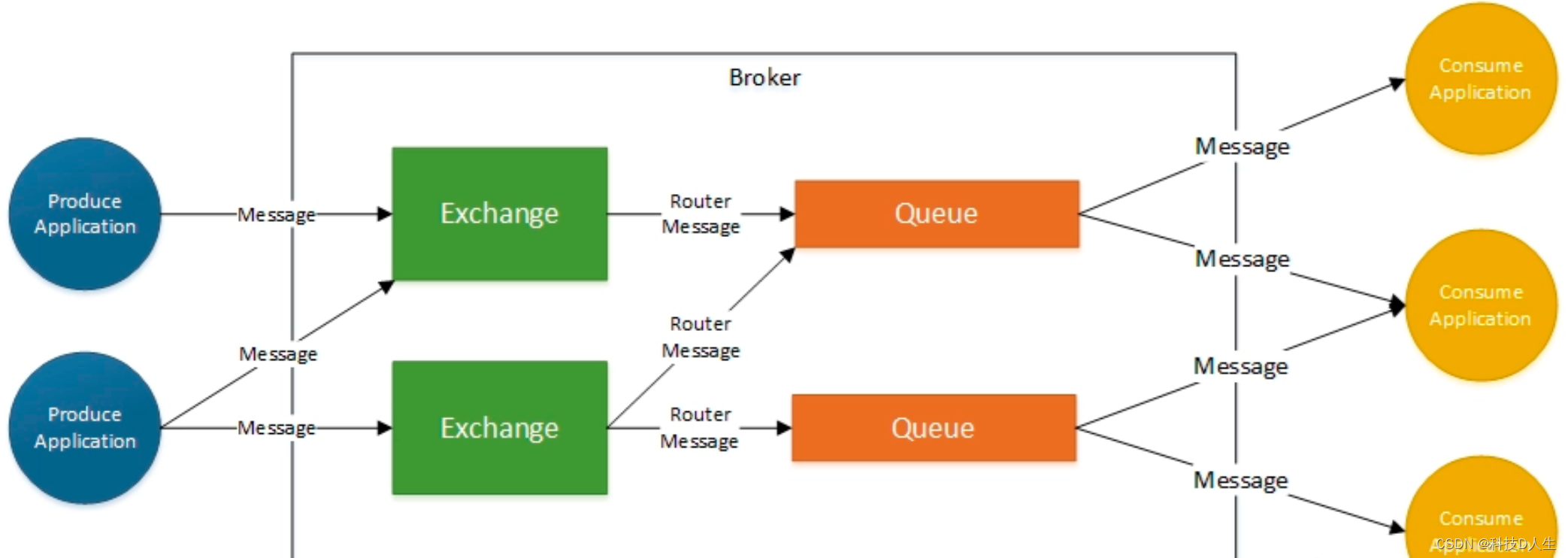
一、丢失场景 RabbitMQ丢失的以下3种情况: (1)生产者:生产者发送消息至MQ的数据丢失...

购物车案例【版本为vue3】
前言: 首先我们要明白整个购物车的组成。它是由一个主页面加两个组件组合成的。本章主要运用父子之间的通讯: 父传子 子传父 首先新建一个vue3项目,这里有俩种创建方式: vue-cli : ● 输入安装指令 npm init vuelates…...

Multisim14 安装包及安装教程
Multisim14 安装教程 Multisim14下载地址:Kevin的学习站–安装包下载地址 Multisim14 简介: Multisim 14 是美国国家仪器有限公司(National Instrument,NI)推出的以 Windows 为基础、符合工业标准的、具有 SPICE 最佳仿…...

Java实现简单的图书管理系统源码+论文
简单图书管理系统设计(文末附带源码论文) 为图书管理人员编写一个图书管理系统,图书管理系统的设计主要是实现对图书的管理和相关操作,包括3个表: 图书信息表——存储图书的基本信息,包括书号、书名、作者…...
前端调试2
一、用chrome调试(node.js)例:const fs require(fs/promises);(async function() {const fileContent await fs.readFile(./package.json, {encoding: utf-8});await fs.writeFile(./package2.json, fileContent); })();1.先 node index.js 跑一下:2.然…...

AlphaFold 2 处理蛋白质折叠问题
蛋白质是一个较长的氨基酸序列,比如100个氨基酸的规模,如此长的氨基酸序列连在一起是不稳定的,它们会卷在一起,形成一个独特的3D结构,这个3D结构的形状决定了蛋白质的功能。 蛋白质结构预测(蛋白质折叠问题…...

问卷调查会遇到哪些问题?怎么解决?
提到问卷调查我们并不陌生,它经常被用作调查市场、观察某类群体的行为特征等多种调查中。通过问卷调查得出的数据能够非常真实反映出是市场的现状和变化趋势,所以大家经常使用这个方法进行调查研究。不过,很多人在进行问卷调查的时候也会遇到…...
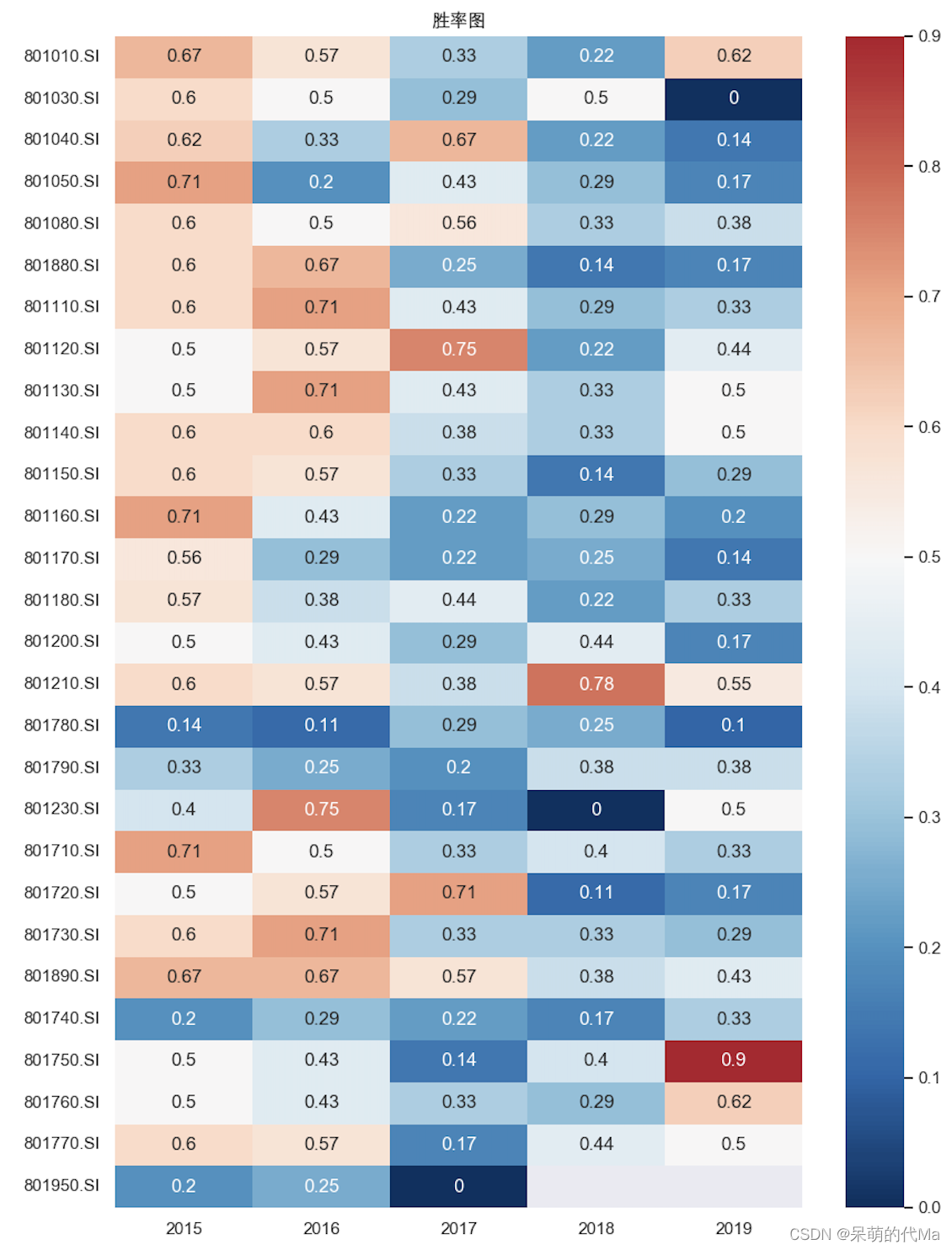
量化选股——基于动量因子的行业风格轮动策略(第1部分—因子测算)
文章目录动量因子与行业轮动概述动量因子的理解投资视角下的行业轮动现象投资者视角与奈特不确定性动量因子在行业风格上的效果测算动量因子效果测算流程概述1. 行业选择:申万一级行业2. 动量因子选择:阿隆指标(Aroon)3. 测算方法…...

工作常用git命令
修改hard:git reset --hard md5git push -f合并多次commitsgit rebase -i HEAD~4git push -f冲突文件被覆盖冲突文件被覆盖了,可以用git checkout commitId /path来快速把一个或一些文件还原会之前的提交,重新commit ,merge一次删除分支git b…...

test3
数据链路层故障分析 一、网桥故障 a.主要用途简述 网桥作为一种桥接器,可以连接两个局域网。工作在数据链路层,是早期的两端口二层网络设备。可将一个大的VLAN分割为多个网段,或者将两个以上的LAN互联为一个逻辑LAN,使得LAN上的…...

领证啦,立抵3600,软考证书到手后还有很多作用
2022年下半年软考合格证书发放在2023年2月-3月进行,目前已有多个省市开始发证了,比如上海、江苏、辽宁、浙江、山东等地。还没收到领证通知的考生也不要着急,可以关注当地软考办通知。 拿到证书的朋友可以去申请入户,职称评聘&am…...
响应式布局之viewport-超级简单
之前文章CSS布局之详解_故里2130的博客-CSDN博客 上面的文章可以实现响应式布局,根据浏览器的大小变化而变化,但是相对于viewport来说,之前的还是有点复杂,而使用viewport更加的简单。 当我们使用amfe-flexible的时候࿰…...

分布式计算考试资料
第一章 分布式系统的定义 分布式系统是一个其硬件或软件组件分布在连网的计算机上,组件之间通过传递信息进行通信和动作协调的系统。分布式系统的目标 资源共享(resource sharing) 一些计算机通过网络连接起来,并在这个范围内有效地共享资源。 硬件的共…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
