深度学习查漏补缺:1.梯度消失、梯度爆炸和残差块
一、梯度消失
梯度消失的根本原因在于 激活函数的性质和链式法则的计算:
-
激活函数的导数很小:
- 常见的激活函数(例如 Sigmoid 和 Tanh)在输入较大或较小时,输出趋于饱和(Sigmoid 的输出趋于 0 或 1),其导数接近于 0。
- 在反向传播中,每一层的梯度都会乘以激活函数的导数。如果导数很小,乘积就会导致梯度逐渐变小。
-
链式法则的多次相乘:
假设网络有 nn 层,梯度从输出层传到第 ii 层时,会经历多次链式相乘:-
如果每一项的导数都小于 1(例如 0.5),那么多次相乘后梯度将变得非常小,接近于 0。
-
-
深层网络的结构:
层数越多,梯度消失的积累效应越明显,导致靠近输入层的权重几乎无法更新。
1.4 梯度消失带来的问题
- 网络无法有效学习:靠近输入层的权重无法更新,网络的学习能力只集中在靠近输出层的部分,导致模型性能受限。
- 训练时间增加:梯度很小,优化器调整参数的速度变慢,训练需要更多的时间。
二、梯度爆炸
1 梯度爆炸的现象
与梯度消失相反,当网络层数较深时,梯度在反向传播过程中可能会逐渐变大,甚至变得非常大。这种现象被称为梯度爆炸。
由于梯度过大,模型的参数更新幅度也会非常大,可能导致:
- 参数出现巨大波动,训练过程不稳定;
- 损失值(Loss)变得非常大,甚至出现
NaN; - 模型无法收敛,最终无法学习任何规律。
2 为什么会发生梯度爆炸?
梯度爆炸的原因与梯度消失类似,主要是由于链式法则的多次相乘,但此时乘积中的值大于 1:
-
权重初始化不当:
- 如果网络的初始权重过大,在反向传播时,梯度的值也会变得很大。
- 例如,如果每层的权重初始化为 5,经过 10 层的链式积累,梯度可能会变成
-
激活函数的导数较大:
- 如果激活函数的导数值很大,梯度在多次相乘后会迅速变大。
-
深层网络的结构:
- 网络层数越多,链式法则的积累效应越明显,导致梯度爆炸的概率增大。
3 梯度爆炸带来的问题
- 训练不稳定:梯度过大,导致参数更新过快,训练过程可能无法收敛。
- 损失发散:梯度爆炸会导致损失值发散,模型无法学习有效特征。
三、残差块
残差块(Residual Block)是深度学习中 ResNet(Residual Network) 网络的核心组件,它最早由微软研究院的何凯明(Kaiming He)等人在 2015 年提出。残差块通过引入跳跃连接(skip connection),解决了深层神经网络训练中的梯度消失、梯度爆炸和退化问题,使得网络能够训练得更深、性能更好。
为什么需要残差块?
在深层神经网络中,随着网络深度的增加(层数增多),存在以下问题:
- 梯度消失(Vanishing Gradient):反向传播时,梯度在逐层传递过程中可能逐渐变小,从而无法有效更新靠近输入层的权重。
- 梯度爆炸(Exploding Gradient):反之,梯度可能会在逐层传递过程中变得过大,导致模型训练不稳定。
- 退化问题(Degradation Problem):当网络层数增加时,模型的训练误差反而会变大,甚至性能比浅层网络更差。
这些问题的根本原因在于,随着层数增加,网络在拟合复杂非线性变换时可能会难以优化。残差块通过引入跳跃连接,允许网络直接学习相对较小的残差(Residual),从而降低优化难度。
残差块的结构
一个标准的残差块具有以下结构:
- 主路径(Main Path):通过若干个卷积、批归一化(Batch Normalization)、激活函数(如 ReLU)组成,是网络的主要信息传递路径。
- 跳跃连接(Skip Connection):从输入直接添加到输出,为网络提供了一条“捷径”。
输出形式为:
y=F(x)+x
其中:
- x:残差块的输入。
- F(x):主路径中卷积、激活等操作的输出。
- y:残差块的最终输出。
通过直接将输入 x 加到输出 F(x) 上,残差块能够显式学习 F(x)=H(x)−x,即学习输入与目标值之间的残差。如果 H(x) 是目标映射函数,那么 F(x)F(x) 是残差函数。
1. 一般形式的残差块
以两个卷积层为例,残差块的结构如下:
- 输入:x
- 第一层卷积(Conv1d/Conv2d),带激活函数(如 ReLU)。
- 第二层卷积(Conv1d/Conv2d)。
- 跳跃连接:直接将 xx 与经过两层卷积后的结果相加。
- 激活函数(如 ReLU)。
数学表达式为:
y=ReLU(F(x)+x)
2. 带维度变换的残差块
如果输入和输出的特征维度不同(例如通道数或空间维度变化),需要使用额外的线性变换对输入 x 进行升维或降维(Projection Shortcut),使得尺寸匹配。
y=F(x)+Ws x
其中 Ws是一个线性变换(通常是 1×1 卷积)。
直观解释残差块的作用
1. 更容易优化深层网络
通过学习残差 F(x)=H(x)−x,残差块将复杂的非线性映射 H(x)转换为一个简单的优化问题。即使网络层数增加,残差块可以将输入直接传递到更深层,减轻梯度消失的影响。
2. 提供信息的捷径
跳跃连接允许信息直接从输入传递到输出,让网络更容易捕捉重要的特征,同时保留原始特征。
3. 防止退化问题
在普通深层网络中,增加更多的层可能会导致模型性能退化,反而不如浅层网络。残差块通过添加跳跃连接,可以显式地学习哪些层需要参与计算,哪些层可以跳过,从而有效防止退化。
相关文章:
深度学习查漏补缺:1.梯度消失、梯度爆炸和残差块
一、梯度消失 梯度消失的根本原因在于 激活函数的性质和链式法则的计算: 激活函数的导数很小: 常见的激活函数(例如 Sigmoid 和 Tanh)在输入较大或较小时,输出趋于饱和(Sigmoid 的输出趋于 0 或 1…...

【Numpy核心编程攻略:Python数据处理、分析详解与科学计算】2.2 多维数组切片:跨步访问与内存布局
2.2 多维数组切片:跨步访问与内存布局 目录/提纲 #mermaid-svg-FbBIOMVivQfdX2LJ {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-FbBIOMVivQfdX2LJ .error-icon{fill:#552222;}#mermaid-svg-FbBIOMVivQ…...

ResNet--深度学习中的革命性网络架构
一、引言 在深度学习的研究和应用中,网络架构的设计始终是一个关键话题。随着计算能力和大数据的不断提升,深度神经网络逐渐成为解决复杂任务的主流方法。然而,随着网络层数的增加,训练深度神经网络往往面临梯度消失或梯度爆炸的…...

TypeScript语言的语法糖
TypeScript语言的语法糖 TypeScript作为一种由微软开发的开源编程语言,它在JavaScript的基础上添加了一些强类型的特性,使得开发者能够更好地进行大型应用程序的构建和维护。在TypeScript中,不仅包含了静态类型、接口、枚举等强大的特性&…...
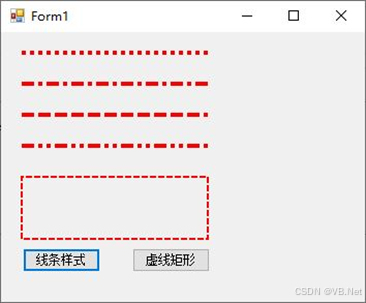
17.2 图形绘制4
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 17.2.5 线条样式 C#为画笔绘制线段提供了多种样式:一是线帽(包括起点和终点处)样式;…...

tomcat核心组件及原理概述
目录 1. tomcat概述 1.1 概念 1.2 官网地址 2. 基本使用 2.1下载 3. 整体架构 3.1 核心组件 3.2 从web.xml配置和模块对应角度 3.3 如何处理请求 4. 配置JVM参数 5. 附录 1. tomcat概述 1.1 概念 什么是tomcat Tomcat是一个开源、免费、轻量级的Web服务器。 Tomca…...

本地部署DeepSeek教程(Mac版本)
第一步、下载 Ollama 官网地址:Ollama 点击 Download 下载 我这里是 macOS 环境 以 macOS 环境为主 下载完成后是一个压缩包,双击解压之后移到应用程序: 打开后会提示你到命令行中运行一下命令,附上截图: 若遇…...

MyBatis-Plus笔记-快速入门
大家在日常开发中应该能发现,单表的CRUD功能代码重复度很高,也没有什么难度。而这部分代码量往往比较大,开发起来比较费时。 因此,目前企业中都会使用一些组件来简化或省略单表的CRUD开发工作。目前在国内使用较多的一个组件就是…...

爬取豆瓣书籍数据
# 1. 导入库包 import requests from lxml import etree from time import sleep import os import pandas as pd import reBOOKS [] IMGURLS []# 2. 获取网页源代码 def get_html(url):headers {User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36…...

基于微信小程序的电子商城购物系统设计与实现(LW+源码+讲解)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

6-图像金字塔与轮廓检测
文章目录 6.图像金字塔与轮廓检测(1)图像金字塔定义(2)金字塔制作方法(3)轮廓检测方法(4)轮廓特征与近似(5)模板匹配方法6.图像金字塔与轮廓检测 (1)图像金字塔定义 高斯金字塔拉普拉斯金字塔 高斯金字塔:向下采样方法(缩小) 高斯金字塔:向上采样方法(放大)…...

【Ai】DeepSeek本地部署+Page Assist图形界面
准备工作 1、ollama,用于部署各种开源模型,并开放接口的程序 https://ollama.com/download 2、deepseek-r1:32b 模型 https://ollama.com/library/deepseek-r1:32b 不同的模型版本对计算机性能的要求不一样,版本越高对显卡和内存的要求越高…...

【最长不下降子序列——树状数组、线段树、LIS】
题目 代码 #include <bits/stdc.h> using namespace std; const int N 1e510; int a[N], b[N], tr[N];//a保存权值,b保存索引,tr保存f,g前缀属性最大值 int f[N], g[N]; int n, m; bool cmp(int x, int y) {if(a[x] ! a[y]) return a[x] < a[…...

【实战篇章】深入探讨:服务器如何响应前端请求及后端如何查看前端提交的数据
文章目录 深入探讨:服务器如何响应前端请求及后端如何查看前端提交的数据一、服务器如何响应前端请求HTTP 请求生命周期全解析1.前端发起 HTTP 请求(关键细节强化版)2. 服务器接收请求(深度优化版) 二、后端如何查看前…...

Games104——引擎工具链基础
总览 工具链 用户到引擎架构图 工具链是衔接不同岗位、软件之间的桥梁,比如美术与技术,策划与美术,美术软件与引擎本身等,有Animation、UI、Mesh、Shader、Logical 、Level Editor等等。一般商业级引擎里的工具链代码量是超过…...

分层多维度应急管理系统的设计
一、系统总体架构设计 1. 六层体系架构 #mermaid-svg-QOXtM1MnbrwUopPb {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-QOXtM1MnbrwUopPb .error-icon{fill:#552222;}#mermaid-svg-QOXtM1MnbrwUopPb .error-text{f…...

【漏斗图】——1
🌟 解锁数据可视化的魔法钥匙 —— pyecharts实战指南 🌟 在这个数据为王的时代,每一次点击、每一次交易、每一份报告背后都隐藏着无尽的故事与洞察。但你是否曾苦恼于如何将这些冰冷的数据转化为直观、吸引人的视觉盛宴? 🔥 欢迎来到《pyecharts图形绘制大师班》 �…...

(二)QT——按钮小程序
目录 前言 按钮小程序 1、步骤 2、代码示例 3、多个按钮 ①信号与槽的一对一 ②多对一(多个信号连接到同一个槽) ③一对多(一个信号连接到多个槽) 结论 前言 按钮小程序 Qt 按钮程序通常包含 三个核心文件: m…...

【Linux】从硬件到软件了解进程
个人主页~ 从硬件到软件了解进程 一、冯诺依曼体系结构二、操作系统三、操作系统进程管理1、概念2、PCB和task_struct3、查看进程4、通过系统调用fork创建进程(1)简述(2)系统调用生成子进程的过程〇提出问题①fork函数②父子进程关…...

HTB:Alert[WriteUP]
目录 连接至HTB服务器并启动靶机 信息收集 使用rustscan对靶机TCP端口进行开放扫描 使用nmap对靶机TCP开放端口进行脚本、服务扫描 使用nmap对靶机TCP开放端口进行漏洞、系统扫描 使用nmap对靶机常用UDP端口进行开放扫描 使用ffuf对alert.htb域名进行子域名FUZZ 使用go…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
